1 Introduction

The production of carbon and heavier elements in stars is complicated by the instability of the \(^8\)Be nucleus. The way this bottleneck is circumvented in nature is by means of the triple-alpha process, where the production rate of \(^{12}\)C is strongly enhanced by a fortuitously placed \(0^+\) resonance, known as the Hoyle state [1]. As small ad hoc changes in the excitation energy of the Hoyle state relative to the triple-alpha threshold can lead to large changes in the reaction rate, and hence (presumably) to the relative abundance of carbon and oxygen, the question arises whether the universe should be regarded as fine-tuned with respect to the likelihood of carbon-oxygen based life to arise. For a recent review on fine-tunings, see Ref. [2]. The triple-alpha process has recently been studied using nuclear lattice effective field theory (NLEFT). The ground state energies of \(^4\)He, \(^8\)Be and \(^{12}\)C, and the energy of the Hoyle state of \(^{12}\)C, were all found to be strongly correlated with respect to small changes in the fundamental constants of nature, an effect of the clustering of alpha particles in the respective nuclei. We review here how the sensitivity of the triple-alpha reaction rate with respect to small changes in the light quark mass and the electromagnetic fine-structure constant is treated in the effective field theory (EFT) framework. The main source of uncertainty is due to the short-range part of the nucleon-nucleon interaction, and we discuss recent progress in narrowing down this uncertainty using updated theoretical knowledge of the quark mass dependence of the two-nucleon S-wave scattering parameters, including the results of recent lattice QCD work. We also contrast this theoretical treatment with recent high-precision calculations of stellar nucleosynthesis, which find that the allowable range of Hoyle state energies is larger than previously thought [3].

This paper is structured as follows: In Sect. 2, we update the pion (or quark) mass dependence of the nuclear Hamiltonian, which is central for the discussion which follows. In Sect. 3, we review the current status of stellar nucleosynthesis calculations, with focus on the resulting abundances of carbon and oxygen under ad hoc shifts in the Hoyle state resonance. In particular, we pay attention to recent new results in this field. In Sect. 4, we revisit the theoretical status of EFT calculations of the sensitivity of the Hoyle state energy to small changes in the light quark mass \(m_q\) and the electromagnetic fine-structure constant \(\alpha _{\mathrm {em}}\). Finally, in Sect. 5 we discuss how the EFT treatment of the triple-alpha process could be improved with regards to recent progress in the nuclear lattice EFT description of the nuclear forces.

2 Quark mass dependence of the nuclear Hamiltonian

The ground-state energies and the spectra of light and medium-mass nuclei can be calculated to good precision in the framework of NLEFT, as described in detail in the monograph [4]. The effects of variations of fundamental parameters, such as the average light quark mass or the electromagnetic fine-structure constant, can also be studied within NLEFT. In what follows, we update our knowledge of the quark mass dependence of the nuclear Hamiltonian, which is central to the study of fine-tunings in the triple-alpha process. As the Gell-Mann–Oakes–Renner relation \(M_\pi ^2 \sim m_q\), where \(m_q =(m_u+m_d)/2\) is the average light quark mass, is fulfilled to high accuracy in QCD, the notions of “quark mass dependence” and “pion mass dependence” can be used synonymously. This update concerns in particular the hadronic parameters \(x_1\) and \(x_2\) and the nuclear parameters \({\bar{A}}_s\) and \({\bar{A}}_t\). For details, the reader is referred to Refs. [4,5,6].

We first discuss \(x_1\), which describes the dependence of the nucleon mass \(m_N\) on the pion mass \(M_\pi \). This is related to the pion–nucleon \(\sigma \)-term \(\sigma _{\pi N}\), via

$$\begin{aligned} x_1^{} \equiv \left. \frac{\partial m_N^{}}{\partial M_\pi ^{}}\right| _{M_\pi ^{\mathrm {ph}}} = 2\frac{\sigma _{\pi N}^{}}{M_\pi ^{}}, \end{aligned}$$
(1)

with \(M_\pi ^{\mathrm {ph}}\) denoting the physical value of the pion mass. Note that the best determinations of \(\sigma _{\pi N}\) are from the recent Roy–Steiner-equation analyses of pion–nucleon scattering, leading to \(\sigma _{\pi N} = (59.1 \pm 3.5)\) MeV [7] (with the inclusion of pionic hydrogen and deuterium data) and \(\sigma _{\pi N} = (58 \pm 5)\) MeV [8] (with pion–nucleon scattering data only). To be on the conservative side, we take the central value of Ref. [7] and the uncertainty of Ref. [8]. While this gives

$$\begin{aligned} x_1^{} = 0.84(7), \end{aligned}$$
(2)

we note that lattice QCD determinations [9,10,11,12,13] give systematically smaller values for \(\sigma _{\pi N}\), and thus for \(x_1\). For reasons explained in Ref. [14], such as the inconsistency of the lattice QCD values with the precisely determined S-wave pion–nucleon scattering lengths, we do not consider these lattice QCD results here.

Next, we turn to \(x_2\), which describes the dependence of the strength of the one-pion exchange (OPE) \(g_A/(2F_\pi )\) on \(M_\pi \). This is given by

$$\begin{aligned} x_2^{} \equiv \frac{1}{2 F_\pi ^{}} \left. \frac{\partial g_A^{}}{\partial M_\pi ^{}}\right| _{M_\pi ^{\mathrm {ph}}} - \frac{g_A^{}}{2 F_\pi ^2} \left. \frac{\partial F_\pi ^{}}{\partial M_\pi ^{}}\right| _{M_\pi ^{\mathrm {ph}}}. \end{aligned}$$
(3)

In Ref. [6], \(x_2\) turned out to be small and of indeterminate sign. This was largely due to the inconclusive situation of lattice QCD calculations of \(g_A\). Such problems have recently been overcome by high-precision lattice QCD calculations with close-to-physical quark masses [15]. In particular, consistent values of \(g_A\) with minimal model dependence were obtained for a range of polynomial and chiral perturbation theory (ChPT) extrapolations in \(M_\pi \). In order to make use of the analysis of Ref. [15], we define

$$\begin{aligned} \frac{\partial g_A^{}}{\partial M_\pi ^{}} \equiv \frac{\partial g_A^{}}{\partial M_*^{}} \frac{\partial M_*^{}}{\partial M_\pi ^{}}, \end{aligned}$$
(4)

where

$$\begin{aligned} M_*^{} \equiv \frac{M_\pi ^{}}{4\pi F_\pi ^{}}, \end{aligned}$$
(5)

and

$$\begin{aligned} \frac{\partial M_*^{}}{\partial M_\pi ^{}} = \frac{1}{4\pi F_\pi ^{}} \left( 1 - \frac{M_\pi ^{}}{F_\pi ^{}} \frac{\partial F_\pi ^{}}{\partial M_\pi ^{}} \right) , \end{aligned}$$
(6)

in terms of which

$$\begin{aligned} g_A^{} = 1.273(19), \qquad \left. \frac{\partial g_A^{}}{\partial M_*^{}}\right| _{M_\pi ^{\mathrm {ph}}} = -0.08(24), \end{aligned}$$
(7)

were obtained from an extrapolation using the complete NNLO chiral expression, with and without inclusion of the N3LO contact terms [16]. It should be noted that unlike the determination of \(g_A\) itself, the value of \(\partial g_A/\partial M_*\) does depend significantly on the choice of extrapolation of the lattice QCD data. For instance, significantly larger values can be obtained by means of linear or quadratic extrapolations in \(M_*\). However, we shall here rely on the chiral NNLO result (7), in particular as it was found to show good convergence of the chiral expansion [15].

The dependence of \(F_\pi \) on \(M_\pi \) was not yet obtained in Ref. [15]. We recall that Ref. [17] provided

$$\begin{aligned} \left. \frac{\partial F_\pi ^{}}{\partial M_\pi ^{}}\right| _{M_\pi ^{\mathrm {ph}}} = 0.066(16), \end{aligned}$$
(8)

which was used in Ref. [6]. This should be compared with the sub-leading order ChPT result

$$\begin{aligned} \frac{\partial F_\pi ^{}}{\partial M_\pi ^{}} = \frac{M_\pi ^{}}{8\pi ^2 F} {\bar{\ell }}_4^{}, \end{aligned}$$
(9)

where \(F \simeq 86.2\) MeV denotes \(F_\pi \) in the chiral limit, and \({\bar{\ell }}_4 = 4.3(3)\) from the review [18]. We note that Eq. (9) gives a number comparable with (though slightly larger than) Eq. (8). These values are also consistent with the most recent FLAG lattice QCD determination [19].

Using the isospin-averaged pion mass \(M_\pi = 138.03\) MeV and \(F_\pi = 92.1\) MeV, we find

$$\begin{aligned} \left. \frac{\partial M_*^{}}{\partial M_\pi ^{}}\right| _{M_\pi ^{\mathrm {ph}}} = 0.078(2) \, {\mathrm {l.u.}}, \end{aligned}$$
(10)

from Eq. (6), for an inverse spatial lattice spacing of \(a^{-1} \equiv 100\) MeV. So far, from Eqs. (3) and (8), we have

$$\begin{aligned} x_2^{} = -0.050(12) \, {\mathrm {l.u.}} + \frac{1}{2 F_\pi ^{}} \left. \frac{\partial g_A^{}}{\partial M_\pi ^{}}\right| _{M_\pi ^{\mathrm {ph}}}, \end{aligned}$$
(11)

where we can now use the chiral lattice QCD extrapolations (7) together with Eq. (10). This gives

$$\begin{aligned} \left. \frac{\partial g_A^{}}{\partial M_\pi ^{}}\right| _{M_\pi ^{\mathrm {ph}}} = -0.006(19) \, {\mathrm {l.u.}}, \end{aligned}$$
(12)

such that we finally obtain

$$\begin{aligned} x_2^{} = -0.053(16) \, {\mathrm {l.u.}}, \end{aligned}$$
(13)

from Eq. (3), which is compatible with the range \(x_2 = -0.056 \ldots 0.008 \, {\mathrm {l.u.}}\) used in Ref. [6]. However, in contrast to the earlier determination of \(x_2\), we can now pin it down with a definite sign up to \(\simeq 3.3\sigma \).

Table 1 Available lattice QCD results for the deuteron and dineutron binding energies obtained from the plateau method, along with the resulting values of the inverse scattering lengths calculated from the LETs at NLO. The uncertainties in the energies are taken from the corresponding papers. The first error of \(a^{-1}_{s,t}\) reflects the uncertainty of the lattice results for the binding energies used as input (for \(M_\pi = 300\), 390 and 510 MeV, with the different lattice errors for the binding energies added in quadrature), while the second error corresponds to the uncertainty of the LETs, estimated as explained in Ref. [35]
Full size table

Having fixed the hadronic input parameters, we now consider the leading order four-nucleon contact interactions that can be mapped onto the derivatives

$$\begin{aligned} {\bar{A}}_{s,t}^{} \equiv \frac{\partial a_{s,t}^{-1}}{\partial M_\pi ^{}}\biggl |_{M_\pi ^{{\mathrm{ph}}}}, \end{aligned}$$
(14)

of the inverse singlet and triplet neutron-proton scattering lengths. Earlier, modeling based on resonance saturation [20] was used to get a handle on these quantities, as discussed in detail in Ref. [17]. Here, we attempt to fix \({\bar{A}}_{s,t}^{}\) from available lattice QCD data, which should be the method of choice. Before doing so, some words of caution are in order. The situation with lattice QCD simulations in the nucleon-nucleon (NN) sector is at present highly controversial. Fully dynamical simulations at unphysically heavy pion masses have been carried out by the NPLQCD Collaboration and Yamazaki et al., based on the standard approach to extract the ground state energy by fitting plateaus of the correlation functions. Such studies find more attraction (in both the \(^1\)S\(_0\) and \(^3\)S\(_1\) channels) at heavy pion masses than for physical pion masses, see Refs. [21,22,23,24,25]. This contradicts the findings of the HAL QCD Collaboration using a (scheme-dependent) potential at an intermediate stage in the extraction of NN observables. The HAL QCD studies found no bound states in either of the S-wave channels, for pion masses ranging from 469 MeV to 1171 MeV [26]. The HAL QCD Collaboration has already carried out simulations at the physical point as well, but the results for the non-strange channels have, as far as we are aware, not yet been released.

The HAL QCD Collaboration has criticized the standard approach by pointing out the danger of observing spurious plateaus [27, 28]. See, however, the response of the NPLQCD Collaboration in Ref. [29]. The HAL QCD approach has also been criticized e.g. in Refs. [30, 31]. The weakest point of the HAL QCD approach seems to be its reliance on a derivative expansion, the convergence of which is not a priori clear. Interestingly, the recent lattice QCD study in the strangeness \(S= -2\) two-baryon sector by the CERN-Mainz group [32], using a superior method of analysis, finds for \(M_\pi = 960\) MeV an H-dibaryon energy, which is perfectly consistent with HAL QCD, but in strong disagreement with NPLQCD.

Fig. 1
figure 1

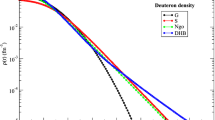
Pion mass dependence of the inverse scattering lengths \(a_{s,t}^{-1}\) as predicted by the lattice QCD calculations of Refs. [21,22,23,24,25]. Black squares show the experimental values at the physical point. Solid (black) and dashed (blue) lines denote quadratic and cubic interpolations, respectively

Full size image

Recently, in Ref. [33], the use of low-energy theorems (LETs) to reconstruct the energy dependence of the NN scattering amplitude in a large kinematical domain from a single observable (e.g. binding energy, scattering length, or effective range) at a given fixed value of \(M_\pi \), was proposed. This method relies on the dominance of the one-pion exchange (OPE) at large distances, which governs the near-threshold energy dependence of the scattering amplitude. At the physical point, LETs are known to work accurately in the \(^3\)S\(_1\) channel (in line with the strong tensor interaction induced by the OPE), while less accurately in the \(^1\)S\(_0\) partial wave (where the OPE potential is very weak) [34]. Note that this approach employs lattice QCD results to determine the strength of the OPE potential at unphysical values of \(M_\pi \), and does not rely on the chiral expansion. At heavy pion masses \(M_\pi \sim M_\rho \), the LETs lose their predictive power, and the approach becomes equivalent to the effective range expansion. In Ref. [33], the LETs were used to test the linear interpolation of \(M_\pi r\), with r the effective range, as a function of \(M_\pi \) between \(M_\pi ^{{\mathrm{ph}}}\) and \(M_\pi \simeq 800\) MeV conjectured by the NPLQCD Collaboration [24]. This study was restricted to the \(^3\)S\(_1\) channel. The assumed linear interpolation was indeed found to be consistent with the available lattice QCD results for the deuteron binding energy obtained using the plateau method, see Fig. 6 of Ref. [33]. In Ref. [35], the LETs were applied to test the consistency between the bound state energies and phase shifts obtained using the Lüscher method by the NPLQCD Collaboration at \(M_\pi = 450\) MeV [23] in both the \(^1\)S\(_0\) and \(^3\)S\(_1\) channels. It was found that the NPLQCD phase shifts were inconsistent with their own results for the deuteron and dineutron energies. This inconsistency was later re-emphasized by the HAL QCD Collaboration using the effective range expansion [27, 28].

With these drawbacks and inconsistencies in mind, we nevertheless go forward and analyze the available lattice-QCD results for the deuteron and dineutron binding energy of Refs. [21,22,23,24,25], which appear mutually consistent, in order to extract the quantities \({\bar{A}}_s\) and \({\bar{A}}_t\). The best way to extract \({\bar{A}}_{s,t}\) is to use the LETs to compute the inverse scattering lengths from the binding energies at the corresponding values of \(M_\pi \), and to perform a subsequent interpolation. In Table 1, we collect the binding energies of the deuteron and dineutron states from the calculations of Refs. [21,22,23, 25] and the resulting values of the inverse scattering lengths. We also include the direct determination of the scattering lengths at \(M_\pi \simeq 806\) MeV by NPLQCD from Ref. [24], which is

$$\begin{aligned} a_t^{-1} = 0.549(59) \text{ fm }^{-1}, \quad a_s^{-1} = 0.429(54) \text{ fm }^{-1}. \end{aligned}$$
(15)

To perform an interpolation between these five data points and the experimental inverse scattering lengths, we use the quadratic ansatz

$$\begin{aligned} a_{s,t}^{-1} (M_\pi ^{}) = (a_{s,t}^{{\mathrm{ph}}})^{-1} + a (M_\pi ^{} - M_\pi ^{{\mathrm{ph}}}) + b (M_\pi ^{} - M_\pi ^{{\mathrm{ph}}})^2, \end{aligned}$$
(16)

where the free coefficients a, b are determined from a least-squares fit to the available values of \(a_{s,t}^{-1}\) at heavier-than-physical pion masses. The resulting fits are shown by the solid (black) lines in Fig. 1. With \(\chi ^2/N_{{\mathrm{DOF}}} = 4.3\) and 2.4 in the singlet and triplet channels respectively, the quality of the fit is marginal. Using a third-degree polynomial leads to the results shown by the dotted (blue) lines, but the \(\chi ^2/N_{{\mathrm{DOF}}}\) is then well below unity, which indicates overfitting. The large values of \(\chi ^2/N_{{\mathrm{DOF}}}\) with a quadratic fit are likely due to underestimated error bars of the lattice QCD results, especially the ones from Ref. [22] at \(M_\pi = 300\) MeV. In any case, we obtain \({\bar{A}}_s \simeq 0.54\) and \({\bar{A}}_t \simeq 0.33\) based on the quadratic interpolation. The cubic extrapolation gives \({\bar{A}}_s \simeq 0.78\) and \({\bar{A}}_t \simeq 0.49\), and we take the difference between the two as a rough estimate of the uncertainty in \({\bar{A}}_{s,t}\). To summarize, the available determinations of \({\bar{A}}_{s,t}\) are

  1. 1.

    Original estimation of Refs. [6, 17]:

    $$\begin{aligned} {\bar{A}}_s = 0.29^{+0.25}_{-0.23}, \quad {\bar{A}}_t = -0.18^{+0.10}_{-0.10}, \quad \end{aligned}$$
    (17)
  2. 2.

    LO chiral EFT of Ref. [36]:

    $$\begin{aligned} {\bar{A}}_s = 0.50(23), \quad {\bar{A}}_t = -0.12(8), \qquad \end{aligned}$$
    (18)
  3. 3.

    Interpolation of lattice QCD data from Refs. [21,22,23,24,25]:

    $$\begin{aligned} {\bar{A}}_s = 0.54(24), \quad {\bar{A}}_t = 0.33(16). \qquad \end{aligned}$$
    (19)

The LO chiral EFT result (18) corresponds to a renormalizable expression for the scattering amplitude with the static OPE, and the uncertainty is estimated from the cutoff variation from \(\varLambda = 600\) MeV to infinity. The positive sign of \({\bar{A}}_t\) in Eq. (19) is consistent with a stronger attraction in the deuteron channel at heavy \(M_\pi \). HAL QCD results would presumably yield a negative value of \({\bar{A}}_t\). In what follows, we use the interpolated lattice QCD values in Eq. (19).

3 The Hoyle state in stellar nucleosynthesis

The stellar synthesis of elements heavier than \(^{4}\)He is complicated by the fact that no stable nucleus exists for \(A = 8\), at least for the physical values of the fundamental constants. In the absence of stable \(^{8}\)Be nuclei, the fusion of He nuclei instead takes place through the triple-alpha reaction 3(\(^{4}\)He) \(\rightarrow \)\(^{12}\)C + \(\gamma \), which requires a number of intermediate steps. The first step is \(^{4}\)He + \(^{4}\)He \(\leftrightarrow \)\(^{8}\)Be, whereby a transient equilibrium population of \(^{8}\)Be is maintained in the stellar core. It should be noted that the unstable \(^{8}\)Be resonance decays back into two alpha particles with a half-life of \(\sim 10^{-16}\) s. The reaction rate for the formation of \(^{8}\)Be is controlled by the energy difference

$$\begin{aligned} \varDelta E_b^{} \equiv E_8^{} - 2 E_4^{}, \end{aligned}$$
(20)

where \(E_4^{}\) and \(E_8^{}\) denote the ground states of \(^{4}\)He and \(^{8}\)Be, respectively. Though \(^{8}\)Be is short-lived, a sufficiently large transient \(^{8}\)Be population in stellar cores is formed to allow for the second step \(^{8}\)Be + \(^{4}\)He \(\rightarrow \)\(^{12}\)C in the triple-alpha process.

In stellar cores composed primarily of He, the non-resonant reaction proceeds too slowly to explain the observed abundances of carbon and oxygen in the universe. However, as the \(^{12}\)C nucleus possesses an excited \(^{12}\)C(\(0_2^+\)) state (known as the Hoyle state) with an empirical excitation energy of 7.6444 MeV, the reaction can also proceed in a resonant manner, which greatly enhances the triple-alpha reaction rate. We define

$$\begin{aligned} \varDelta E_h^{} \equiv E_{12}^\star - E_8^{} - E_4^{}, \end{aligned}$$
(21)

which controls the reaction rate for the second step \(^{8}\)Be + \(^{4}\)He \(\leftrightarrow \)\(^{12}\)C(\(0_2^+\)), where \(E_{12}^\star \) is the (total) energy of the Hoyle state resonance. The energy scale \(E_R\) which controls the resonant triple-alpha reaction is then

$$\begin{aligned} E_R^{} \equiv \varDelta E_b^{} + \varDelta E_h^{} = E_{12}^\star - 3 E_4^{}, \end{aligned}$$
(22)

which is empirically known (in our universe) to be \(E_R^{\mathrm {ph}} = 379.47(18)\) keV. Note that this is much smaller than the binding energies of the nuclei participating in the triple-alpha reaction, which are \(\simeq 28\) MeV for \(^{4}\)He and \(\simeq 92\) MeV for \(^{12}\)C.

For a stellar plasma at temperature T, the reaction rate \(r_{3 \alpha }\) for fusion of three alpha particles via the ground state of \(^8\)Be and the Hoyle state of \(^{12}\)C is

$$\begin{aligned} r_{3 \alpha }^{} = 3^{\frac{3}{2}} N_\alpha ^3 \left( \frac{2 \pi \hbar ^2}{|E_4^{}| k_B^{} T} \right) ^3 \frac{\Gamma _\gamma ^{}}{\hbar } \, \exp \left( -\frac{E_R^{}}{k_B^{} T} \right) , \end{aligned}$$
(23)

where \(N_\alpha \) is the number density of alpha particles, and \(k_B\) is the Boltzmann constant. It should be noted how the exponential dependence on \(E_R\) and \(T^{-1}\) arises, as the observation that the rate of stellar carbon production is exponentially sensitive to \(E_R\) is central to the anthropic picture of the triple-alpha process, for discussions on this issue see [37, 38]. For non-resonant reactions, the corresponding factor is given by the convolution of Coulomb barrier penetration with a thermal distribution of particle velocities, which gives a \(\sim T^{-1/3}\) dependence on temperature. For resonant reactions a fixed energy is singled out, in this case given by Eq. (22), which leads to the exponential dependence of Eq. (23). It should be noted that \(E_R\) is clearly the dominant control parameter of the triple-alpha process, in comparison with the linear dependence on the radiative width \(\Gamma _\gamma \simeq 0.0037\) eV of the Hoyle state. Still, \(\Gamma _\gamma \) should be sufficiently large to allow for the radiative decay of the Hoyle state to be competitive with fragmentation into \(^8\)Be and \(^4\)He. The radiative decay proceeds either through \(^{12}\)C(\(0_2^+\)) \(\rightarrow \)\(^{12}\)C(\(0_1^+\)) + \(\gamma \), or \(^{12}\)C(\(0_2^+\)) \(\rightarrow \)\(^{12}\)C(\(2_1^+\)) + \(\gamma \), after which the \(^{12}\)C(\(2_1^+\)) decays to the ground state \(^{12}\)C(\(0_1^+\)) by emission of a second photon. In practice, this two-step E2 process is more efficient than the direct M0 decay, which is highly suppressed. Interestingly, the channel \(^{12}\)C(\(0_2^+\)) \(\rightarrow \)\(^{12}\)C(\(2_1^+\)) + \(\gamma \) is strongly enhanced compared to the single-particle Weisskopf rate (often referred to as “strongly collective behavior”), which is correctly predicted by recent lattice EFT calculations, see e.g. [4].

We define

$$\begin{aligned} \delta E_R^{} \equiv E_R^{} - E_R^{\mathrm {ph}}, \end{aligned}$$
(24)

when the energy of the Hoyle state is shifted from its physical value. Clearly, for \(\delta E_R > 0\) (the Hoyle state energy is increased), the rate of carbon production (at constant stellar temperature T) is decreased. In order to generate sufficient energy to counteract gravitation, the stellar core must increase T in order to compensate for the reduction in \(r_{3 \alpha }\). It should be noted that the production of \(^{12}\)C via the triple-alpha reaction competes with the destruction of \(^{12}\)C by the formation of \(^{16}\)O through \(^{12}\)C+\(^{4}\)He \(\rightarrow \)\(^{16}\)O\(+\gamma \), such that even a small change in T could lead to a C/O abundance which is very different from that observed. However, the \(^{16}\)O nucleus has a state with excitation energy 7.1187 MeV, which is below the threshold energy of the \(^{12}\)C+\(^{4}\)He system, which is 7.1616 MeV above the ground state of \(^{16}\)O. Hence, the formation of \(^{16}\)O is a non-resonant process, which nevertheless depends sensitively on T because of the sizable Coulomb barrier.

On a phenomenological level, the variation of \(E_R\) leads to a change in the relative importance of the competitive processes by which \(^{12}\)C is produced, and destroyed by further processing into \(^{16}\)O (and heavier alpha nuclei). While the latter processes are non-resonant, the Coulomb barrier which has to be overcome leads to a strong T-dependence of the respective reaction rates. For sufficiently large and positive \(\delta E_R\), a regime exists where most \(^{12}\)C and \(^{16}\)O is processed into heavier nuclei, in particular into \(^{24}\)Mg and \(^{28}\)Si. Conversely, for negative \(\delta E_R\), stellar core temperatures during He burning are substantially lower, which yields large amounts of \(^{12}\)C, but little or no \(^{16}\)O. However, the latter point turns out to be sensitive to the initial stellar metallicity (recall that metallicity gives the proportion of other elements than H and He in stars). Also, when the Hoyle state energy is lowered (\(\delta E_R < 0\)), one should consider the sensitivity

$$\begin{aligned} \varXi _T^{} \equiv \frac{T}{r_{3\alpha }^{}} \frac{d r_{3\alpha }^{}}{dT} = -3 + \frac{E_R^{}}{k_B^{} T}, \end{aligned}$$
(25)

where the stability of the star requires that the triple-alpha reaction rate (and hence the energy production) increase as T increases, such that \(\varXi _T > 0\). Hence, \(E_R\) should satisfy

$$\begin{aligned} E_R^{} > 3k_B^{} T, \end{aligned}$$
(26)

which places a lower bound on the permissible values of the Hoyle state energy. However, as stellar cores have roughly \(k_B T \simeq 10\) keV during He burning, this bound is an order to magnitude smaller than the observed value of \(E_R \simeq 380\) keV.

Recently, comprehensive simulations of stellar nucleosynthesis in massive stars that eventually explode as supernovae have become available [3]. These are based on MESA [39, 40], a comprehensive open-source code package with state-of-the art treatment of the various physical aspects that govern stellar evolution, such as equation of state, opacity, convection, diffusion and thermonuclear as well as weak reaction rates at conditions appropriate for a stellar plasma. In Ref. [3], the evolution of stars ranging from 15 to 40 solar masses were followed up to the stage where a degenerate Fe core is formed. The yields of various isotopes are then weighted according to the stellar mass distribution function, taken to be \(dN/dM_\odot \propto M_\odot ^{-2.3}\) (for the range of stellar masses \(M_\odot \) considered), which accounts for the relative scarcity of heavier stars. For the stellar metallicity, Ref. [3] considered two cases. Firstly, the low-metallicity simulations used \({\mathcal {Z}} = 10^{-4}\), which is representative of the currently known stars with the lowest observed metallicity. Secondly, the case of \({\mathcal {Z}} = {\mathcal {Z}}_{\mathrm {sun}}\) was studied, where \({\mathcal {Z}}_{\mathrm {sun}} = 0.02\) is the observed solar metallicity. The main effect of \({\mathcal {Z}}\) is to alter the relative importance of the p–p chain and the CNO cycle, such that stars can enter the He burning phase with different configurations.

We are now in a position to summarize the findings of Ref. [3] for the range in \(\delta E_R\), for which the final abundances of \(^{12}\)C and \(^{16}\)O exceed their initial values. These can be expressed as

$$\begin{aligned} \delta E_R^{(-)} \le \delta E_R^{} \le \delta E_R^{(+)}, \end{aligned}$$
(27)

where the boundaries for each nucleus depend on the chosen initial stellar metallicity. For \({\mathcal {Z}} = 10^{-4}\) (low metallicity), the ranges compatible with carbon-oxygen based life are

$$\begin{aligned} {\mathrm {^{12}C}} ({\mathcal {Z}} = 10^{-4}): \quad -300~{\mathrm {keV}} \le \delta E_R^{} \le 500~{\mathrm {keV}}, \end{aligned}$$
(28)

and

$$\begin{aligned} {\mathrm {^{16}O}} ({\mathcal {Z}} = 10^{-4}): \quad -300~{\mathrm {keV}} \le \delta E_R^{} \le 300~{\mathrm {keV}}, \end{aligned}$$
(29)

where for negative \(\delta E_R\), sufficient \(^{12}\)C and \(^{16}\)O were produced for all values of the Hoyle state energy compatible with the constraint (26). For \({\mathcal {Z}} = 0.02\) (solar metallicity), the corresponding ranges were found to be significantly narrower. Specifically,

$$\begin{aligned} {\mathrm {^{12}C}} ({\mathcal {Z}} = 0.02): \quad -300~{\mathrm {keV}} \le \delta E_R^{} \le 160~{\mathrm {keV}}, \end{aligned}$$
(30)

and

$$\begin{aligned} {\mathrm {^{16}O}} ({\mathcal {Z}} = 0.02): \quad -150~{\mathrm {keV}} \le \delta E_R^{} \le 200~{\mathrm {keV}}, \end{aligned}$$
(31)

where significant carbon production could still be maintained for all negative \(\delta E_R\). In stars of solar metallicity, the production of \(^{16}\)O appears to be the limiting factor, as it is only possible in a roughly symmetric (though rather broad) envelope centered on the physical value of \(E_R\).

Previously, the stellar simulations of Refs. [41, 42] indicated that sufficient abundances of both carbon and oxygen are only possible for \(\delta E_R \simeq \pm 100\) keV around the empirical value \(E_R= 379.47(18)\) keV. From the present results, we conclude that the energy of the Hoyle state is likely to be less fine-tuned than previously thought. However, if the Hoyle state is raised by more than \(\simeq 300\) keV, the generation of sufficient oxygen would encounter difficulties. Were the Hoyle state located more than \(\simeq 500\) keV above its physical energy, the universe would also be unlikely to contain a sufficient amount of carbon.

4 Sensitivity to small changes in the fundamental parameters

We shall now update the ranges of variation of the light quark mass \(\delta m_q\) and the fine-structure constant \(\delta \alpha _{{\mathrm{em}}}\), which are compatible with stellar production of carbon and oxygen in our universe, and thus with the existence of carbon-oxygen based life. As in Ref. [6], we express the shift in the Hoyle state \(\delta E_R\) as

$$\begin{aligned} \delta E_R^{}&\approx \left. \frac{\partial E_R^{}}{\partial M_\pi ^{}} \right| _{M_\pi ^{\mathrm {ph}}} \delta M_\pi ^{} + \left. \frac{\partial E_R^{}}{\partial \alpha _{{\mathrm{em}}}^{}} \right| _{\alpha _{{\mathrm{em}}}^{\mathrm {ph}}} \delta \alpha _{{\mathrm{em}}}^{} \nonumber \\&\equiv Q_{{\mathrm{q}}}^{}(E_R^{}) \left( \frac{\delta m_q^{}}{m_q^{}}\right) + Q_{{\mathrm{em}}}^{}(E_R^{}) \left( \frac{\delta \alpha _{{\mathrm{em}}}^{}}{\alpha _{{\mathrm{em}}}^{}}\right) , \end{aligned}$$
(32)

for \(| \delta m_q/m_q | \ll 1\) and \(| \delta \alpha _{{\mathrm{em}}}/\alpha _{{\mathrm{em}}} | \ll 1\). We shall first consider the effects of varying \(m_q\), for which we have

$$\begin{aligned} Q_{{\mathrm{q}}}^{}(E_R^{}) \equiv \left. \frac{\partial E_R}{\partial M_\pi ^{}} \right| _{M_\pi ^{\mathrm {ph}}} K_{M_\pi }^q M_\pi ^{}, \end{aligned}$$
(33)

and we recall that \(K_{M_\pi }^q = 0.494^{+0.009}_{-0.013}\) [17]. As in the NLEFT calculation of Ref. [6], we find

$$\begin{aligned} \left. \frac{\partial E_R}{\partial M_\pi ^{}} \right| _{M_\pi ^{\mathrm {ph}}} = -0.572(19) \, {\bar{A}}_s^{} - 0.933(15) \, {\bar{A}}_t^{} + 0.068(7), \end{aligned}$$
(34)

where the only change from Ref. [6] is the constant (last) term, which has been recalculated for the updated values of \(x_1\) and \(x_2\). The numbers in parentheses are Monte Carlo errors. As in Ref. [6], the relatively small additional errors due to the uncertainties of \(x_1\) and \(x_2\) have been neglected. As such uncertainties are much reduced here, this simplification is now better justified.

Fig. 2
figure 2

“Survivability plots” based on the stellar simulations of [41, 42] (Oberhummer et al., bottom right plot) and [2, 3] (all other plots). The data points with horizontal and vertical error bars indicate estimates of where our universe is located. On the solid black lines, \(E_R\) (and hence the triple-alpha reaction) is independent of variations in \(m_q\). The dot-dashed black lines correspond to the equalities (36) and (37), which mark the upper bound \(\delta E_R^{(+)}\) for \(|\delta m_q | / m_q = 1\%\). Similarly, the dotted black lines correspond to the equalities (38) and (39), which mark the lower bound \(\delta E_R^{(-)}\). For the case of \(^{12}\)C and \({\mathcal {Z}} = 0.02\), both \(\delta m_q > 0\) and \(\delta m_q < 0\) are given, for the other cases only \(\delta m_q > 0\) is shown

Full size image

The boundaries of the region where stars are able to produce sufficient carbon or oxygen are given by

$$\begin{aligned} \delta E_R^{(-)} \le Q_{{\mathrm{q}}}^{}(E_R^{}) \left( \frac{\delta m_q^{}}{m_q^{}} \right) \le \delta E_R^{(+)}, \end{aligned}$$
(35)

where the earlier stellar nucleosynthesis calculations of Refs. [41, 42] indicated \(|\delta E_R^{(-)}|\)\(=\)\(|\delta E_R^{(+)}|\)\(=\) 100 keV, from ad hoc variations of the Hoyle state energy. The present situation is slightly more involved, as the upper and lower boundaries are not symmetric, and moreover the boundaries for \(^{12}\)C and \(^{16}\)O are different, an additional factor being the (initial) metallicity of the star under consideration. On the one hand, for \(E_R\) to not increase beyond the permissible range, we require that

$$\begin{aligned}&-0.572(19) \, {\bar{A}}_s^{} - 0.933(15) \, {\bar{A}}_t^{} + 0.068(7) \nonumber \\&\quad \le \frac{\delta E_R^{(+)}}{K_{M_\pi }^q M_\pi ^{}} \left( \frac{|\delta m_q^{}|}{m_q^{}} \right) ^{-1}, \quad \delta m_q^{} > 0, \end{aligned}$$
(36)

for positive shifts in \(m_q\) such that \(\delta m_q \rightarrow |\delta m_q |\), and

$$\begin{aligned}&-0.572(19) \, {\bar{A}}_s^{} - 0.933(15) \, {\bar{A}}_t^{} + 0.068(7) \nonumber \\&\quad \ge -\frac{\delta E_R^{(+)}}{K_{M_\pi }^q M_\pi ^{}} \left( \frac{|\delta m_q^{}|}{m_q^{}} \right) ^{-1}, \quad \delta m_q^{} < 0, \end{aligned}$$
(37)

for negative shifts in \(m_q\) such that \(\delta m_q \rightarrow -|\delta m_q |\). On the other hand, for \(E_R\) to not decrease too much, we should have

$$\begin{aligned}&-0.572(19) \, {\bar{A}}_s^{} - 0.933(15) \, {\bar{A}}_t^{} + 0.068(7) \nonumber \\&\quad \ge \frac{\delta E_R^{(-)}}{K_{M_\pi }^q M_\pi ^{}} \left( \frac{|\delta m_q^{}|}{m_q^{}} \right) ^{-1}, \quad \delta m_q^{} > 0, \end{aligned}$$
(38)

for positive shifts in \(m_q\), and

$$\begin{aligned}&-0.572(19) \, {\bar{A}}_s^{} - 0.933(15) \, {\bar{A}}_t^{} + 0.068(7) \nonumber \\&\quad \le -\frac{\delta E_R^{(-)}}{K_{M_\pi }^q M_\pi ^{}} \left( \frac{|\delta m_q^{}|}{m_q^{}} \right) ^{-1}, \quad \delta m_q^{} < 0, \end{aligned}$$
(39)

for negative shifts in \(m_q\). Hence, the values of \({\bar{A}}_s\) and \({\bar{A}}_t\) compatible with a given variation in \(m_q\) are given by the regions enclosed by Eqs. (36) and (38) for \(\delta m_q^{} > 0\), and by Eqs. (37) and (39) for \(\delta m_q^{} < 0\).

The constraints on \({\bar{A}}_s\) and \({\bar{A}}_t\) from Eqs. (36)–(39) are given by the shaded bands in Fig. 2. These bands cover the values of \({\bar{A}}_s\) and \({\bar{A}}_t\) consistent with the ability of stars to produce \(^{12}\)C and \(^{16}\)O, when \(m_q\) is varied by 0.5%, 1% and 5%, in order. As an example, given the boundaries for \(^{12}\)C production in stars with solar metallicity (\({\mathcal {Z}} = 0.02\)), the interpolated lattice QCD result is compatible with a \(\simeq 0.8\%\) increase in \(m_q\), beyond which \(E_R\) is decreased too much. Conversely, beyond a \(\simeq 0.4\%\) decrease in \(m_q\), \(E_R\) is increased too much. For stars with solar metallicity, the production of \(^{16}\)O is clearly the most heavily constraining factor, although low-metallicity stars (\({\mathcal {Z}} = 10^{-4}\)) allow for much greater variation of \(m_q\). This value of the metallicity corresponds to the metal-poorest stars observed in the universe. In such metal-poor stars, the chiral EFT determinations of \({\bar{A}}_s\) and \({\bar{A}}_t\) suggest that changes of \(\sim 5\%\) in \(m_q\) are permissible. However, from the interpolated lattice QCD results, the allowed range in \(m_q\) is strongly reduced to a mere \(\simeq 0.8\%\), largely because of the positive value of \({\bar{A}}_t\).

Finally, we note that the effect of shifts in the electromagnetic fine-structure constant lead to the constraint

$$\begin{aligned} \frac{|\delta \alpha _{{\mathrm{em}}}^{}|}{\alpha _{{\mathrm{em}}}^{}} \le \frac{|\delta E_R^{}|}{Q_{{\mathrm{em}}}^{}(E_R^{})}, \end{aligned}$$
(40)

where \(Q_{{\mathrm{em}}}(E_R) = 3.99(9)\) MeV was determined in the NLEFT calculation of Ref. [6]. With the bound \(|\delta E_R| = 100\) keV [41, 42], this is compatible with a \(\simeq 2.5\%\) shift in \(\alpha _{{\mathrm{em}}}\). With the much more relaxed bound \(|\delta E_R| = 300\) keV due to the production of \(^{16}\)O in stars with \({\mathcal {Z}} = 10^{-4}\), this tolerance is significantly increased to \(\simeq 7.5\%\).

5 Discussion

We have reconsidered the sensitivity of the triple-alpha process with respect to shifts in the fundamental parameters of nature, especially the light quark mass \(m_q\) and the electromagnetic fine-structure constant \(\alpha _{{\mathrm{em}}}\). Our knowledge of the quark-mass dependence of the hadronic parameters in the nuclear Hamiltonian has improved significantly, in particular with respect to the nucleon axial-vector coupling \(g_A\). There, new lattice QCD data allow for an accurate chiral extrapolation which shows good convergence.

Much more detailed predictions of the effects of ad hoc variation of the position of the energy \(E_R\) of the Hoyle state resonance on the stellar yields of \(^{12}\)C and \(^{16}\)O have also become available. In Ref. [3], the only change made to the MESA code was to manually shift \(E_R\), leaving all other characteristics (such as nuclear binding energies and reaction rates) unaffected. This was taken to be permissible because of the extreme sensitivity of the triple-alpha reaction rate to \(E_R\). Though far beyond the scope of the current work, we note that in principle, NLEFT could be used to compute reaction rates and other nuclear properties at different values of the fundamental parameters. Our present treatment of the triple-alpha process only requires that ad hoc shifts in \(E_R\) be related to shifts in the fundamental constants by means of NLEFT.

The stellar simulations of Ref. [3] show that the production of \(^{16}\)O in low-metallicity stars is likely to be the limiting factor for carbon-oxygen based life, although in general the bounds have become much less stringent. An interesting scenario to consider is also the possibility of a bound \(^8\)Be nucleus, which for physical \(M_\pi \) is unbound by a mere \(\simeq 92\) keV, significantly less than \(E_R \simeq 380\) keV. In that case, \(^{12}\)C and heavier nuclei could be produced without the resonant enhancement provided by the Hoyle state. In NLEFT, the sensitivity of the \(^8\)Be ground state to small changes in the fundamental parameters turns out to be much smaller than that of \(E_R\) [6]. Moreover, the sensitivities of all the relevant \(^4\)He, \(^8\)Be and \(^{12}\)C states to shifts in \(M_\pi \) turn out to be strongly correlated. Hence, \(^8\)Be does not become bound in the region of \(E_R\) found to be compatible with carbon-oxygen based life in Ref. [3].

Since the NLEFT work of Ref. [6], much more lattice QCD data on the singlet and triplet S-wave nucleon scattering lengths at unphysical pion masses has been produced. The current lattice QCD data appear to disfavor the “no-fine-tuning scenario”, to the extent that a relatively small \(\simeq 0.5\%\) shift in \(m_q\) would eliminate carbon-oxygen based life from the universe. On the other hand, such life could possibly persist up to \(\simeq 7.5\%\) shifts in \(\alpha _{{\mathrm{em}}}\). Clearly, more reliable lattice QCD data at close-to-physical pion masses are required to overcome the remaining uncertainties discussed in detail in Sect. 2.

While we have mostly focused on updating the nuclear, hadronic and astrophysical inputs to the EFT calculation of the fine-tuning of the triple-alpha process, it is also of interest to perform improved \(^{12}\)C simulations in NLEFT. Apart from effects of smearing of the LO operators, the NLEFT calculation of the nuclei (and their excited states) involved in the triple-alpha process is essentially a LO calculation. Extending this to higher orders would require much more detailed information on the nuclear force at unphysical pion masses, for higher orders in the EFT expansion. As modern NLEFT potentials (see e.g. Ref. [43]) use a combination of local and non-local smearing of all operators at LO and higher orders, the description of \(^{12}\)C including the Hoyle state is nevertheless expected to be improved.