Fluctuations and clustering of multiplicity in collisions of relativistic ions

Abstract

We discuss the recently measured event-by-event multiplicity fluctuations in relativistic heavy-ion collisions. It is shown that the observed non-monotonic behavior of the scaled variance of the multiplicity distribution as a function of collision centrality can be fully explained by the correlations between produced particles promoting cluster formation (such an effect is not observed in a widely used string-hadronic models of nuclear collisions). We define a cluster as a quasi-neutral gas of charged and neutral particles which exhibits collective behavior. The characteristic space scale of this shielding is the Debye length. The multiplicity distribution in a cluster is given by a negative binomial distribution while the rest (reservoir), treated as a superposition of elementary collisions, is described by a binomial distribution. The ability to generate spatial structures (cluster phase) with self-similar fluctuations of multiplicity sign the propensity to self-organize of hadronic matter.

1 Introduction

The studies of multiplicity fluctuations of particles produced in relativistic ion reactions have been performed extensively since many years, because they may serve as a probe of dynamics present in the particle production mechanism and the possible creation of a quark–gluon plasma.

Collision of relativistic ions leads to the production of a hot quark–gluon plasma, which cools and at $T=155\pm 10$ MeV [1,2,3] transits to a hadron gas of that temperature. The hot quark–gluon system during the transition is effectively quenched by the cold physical vacuum. The so-called self-organized criticality is the appropriate mechanism leading to a universal scale-free behavior [4].

Self-organized criticality (SOC) [5] is a property of nonequilibrium dynamical systems that have a critical point as an attractor (for review, see [6,7,8]). The macroscopic properties of such systems are characterized by the spatial and/or temporal scale-invariance of the phase transition critical point. Unlike equilibrium systems which require the tuning of parameters to enter a critical behavior, nonequilibrium SOC systems tune themselves during evolution in the direction of criticality.¹ A remarkable feature of active matter is the propensity to self-organize. One striking instance of this ability to generate spatial structures is the cluster phase, where clusters broadly distributed in size constantly move and evolve through particle exchange [4].

In the following sections we discuss imprints of multiplicity clustering on charged particles multiplicity fluctuations observed recently by the NA49 and NA61/SHINE experiments located at CERN SPS.

2 Data on multiplicity fluctuations

In this work the multiplicity distribution $P\left( N\right)$ and its scaled variance $\omega$ are used to characterize the multiplicity fluctuations. Let $P\left( N\right)$ denotes the probability to observe a particle multiplicity N in a high-energy nuclear collision. By definition $P\left( N\right)$ is normalized to unity, $\sum _{N} P\left( N\right) =1$. The scaled variance of the multiplicity distribution (the so-called Fano factor), $\omega \left( N\right)$ is defined as

$$\begin{aligned} \omega \left( N\right) =\frac{\text {Var}\left( N\right) }{\langle N\rangle }=\frac{\langle N^{2}\rangle - \langle N\rangle ^{2}}{\langle N\rangle }, \end{aligned}$$

(1)

where $\text {Var}\left( N\right) =\sum _{N}\left( N-\langle N\rangle \right) ^{2}\cdot P\left( N\right)$ is the variance of the distribution and $\langle N\rangle =\sum _{N} N\cdot P\left( N\right)$ is the average multiplicity.

In many models the scaled variance of the multiplicity distribution is independent of the number of particle production sources. Widely used models of nuclear collisions, the so-called superposition models, are based on the concept of particle emission from independent sources. The simplest example is the wounded nucleon model (WNM) [9], in which the sources are wounded nucleons, i.e. the nucleons that have interacted at least once (usually calculated using Glauber model approach). In WNM, the scaled variance in nucleus–nucleus collisions is the same as in nucleon–nucleon interactions provided that the number of wounded nucleons is fixed. Also string-hadronic models predict similar values of $\omega$ for hadronic and nuclear collisions [10]. In a hadron-gas model [11] the scaled variance of the multiplicity distribution converges to a constant value with increasing volume of the system. In the special case of a hadron-gas model, the so-called grand-canonical statistical formulation neglecting quantum effects and resonance decays multiplicity distribution is a Poisson (PD) one, namely

$$\begin{aligned} P_{PD}\left( N\right) =\frac{\langle N\rangle ^{N}}{N!}\cdot \exp \left( -\langle N\rangle \right) . \end{aligned}$$

(2)

The variance of a PD is equal to its mean, and thus the scaled variance is $\omega =1$, independently of average multiplicity. It is then easy to find a possible discrepancy of the measured multiplicity distribution from the PD. ² For a review, see Ref. [12].

The NA49 and NA61/SHINE experiments located at CERN SPS analyzed multiplicity fluctuations of the charged particles produced in p+p, Be+Be, Ar+Sc and Pb+Pb collisions [13,14,15]. Both experiments used scaled variance of the multiplicity distribution, defined in Eq. (1), as a measure of multiplicity fluctuations. The NA49 Collaboration published data on multiplicity fluctuations in Pb+Pb reactions as a function of collision centrality [13]. Unexpectedly, the measured scaled variance show a very non-trivial centrality dependence. It is close to unity at completely central collisions but it manifests a prominent discrepancy from unity at peripheral interactions. The measurement has been performed at the collision center of mass energy $\sqrt{s_{NN}}=17.3$ GeV for particles produced in forward hemisphere in the restricted rapidity inverval $1.1< y_{\pi } < 2.6$³ in the center of mass frame. The azimuthal acceptance has also been limited, and about 17% of all produced charged particles have been used in the analysis [13]. Later on NA49 and NA61/SHINE experiments registered multiplicity distributions of negatively charged particles produced in p+p and the most central (1%) Be+Be, Ar+Sc and Pb+Pb collisions at the same center of mass energy, but emitted to the full forward hemisphere, $y_{\pi }>0$ [14, 15].

In this paper we focus on a description of the centrality dependence of the average multiplicity and scaled variance of the multiplicity distribution of the charged particles produced in Pb+Pb collisions in $1.1< y_{\pi } < 2.6$ as measured by the NA49 Collaboration. We also try to describe data on multiplicity fluctuations in the full forward hemisphere obtained in p+p interactions and the most central (1%) Be+Be, Ar+Sc and Pb+Pb collisions.

3 Model description

Let us specify a cluster as a quasi-neutral gas of electrically charged and neutral particles which displays collective behavior. The characteristic space scale of this shielding is the Debye length (or radius):

$$\begin{aligned} \lambda ^{2}_{D}=\frac{kT}{4\pi e^{2}n} \end{aligned}$$

(3)

where n is the density of the charged particles (mostly pions). Taking the pion radius $r_{\pi }=0.8$ fm [16] and $kT=0.15$ GeV, we have $n=0.46$ fm${}^{-3}$. Consequently, the Debye length is equal to $\lambda _{D}=4.2$ fm. In the Debye sphere of the volume

$$\begin{aligned} V=\frac{4}{3}\pi \lambda ^{3}_{D} \end{aligned}$$

(4)

we have $N\simeq 143$ charged particles, which corresponds at $\sqrt{s_{NN}}=17$ GeV to the number of projectile participants $N_{p}\simeq 18$. The number of particles in the Debye sphere determines the size of the cluster.

The statistical hadronization model is a very efficient tool for the description of average particle multiplicities in high-energy heavy-ion reactions [1, 17,18,19,20,21] as well as in elementary particle reactions [22,23,24]. Within this model there is also the possibility to obtain multiplicity fluctuations since the status of the hadronizing sources is known. The multiplicity and electric charge fluctuations have been proposed as a good selective tool between hadron gas and quark–gluon plasma [25, 26] provided they survive the phase transition and the hadronic system freezes out in a nonequilibrium situation. To properly assess the selective power of such observables, one should first calculate fluctuations in a hadron gas by including the effects of quantum statistics, conservation constraints, etc. The effects of conservation constraints on fluctuations in thermal ensembles were first addressed from the perspective of heavy-ion collisions in Ref. [27]. More recently, it has been pointed out [28, 29] that in the canonical ensemble (CE) with exact conservation of charge, the scaled variance of the multiplicity distribution of any particle does not converge to the corresponding grand-canonical (GCE) value even in the thermodynamic limit, unlike the mean [30, 31].

Fig. 1

Scaled variance of the charged particles multiplicity distribution as a function of average charged multiplicity. By squares and circles we indicate data on particle production in p+p collisions: squares (inelastic data) are from the compilation for beam energy 3.7–303 GeV presented in [33], full circles (non-single diffractive data) are from the compilation in [34]. Open symbols are from data on particle production in jets: open circles are from [35] and open squares from [36, 37]. A line shows our fit to the data

Fig. 2

Distribution of the number of nucleons which emit particles to the cluster, $N_{p}^\text {max}$. See text for details

If we split a CE, or micro-canonical ensemble (MCE) into N subsystems, the variance of any particle multiplicity distribution is not additive, as conservation constraints involve nonvanishing correlations between different subsystems even for large N. Thus, their GCE and CE thermodynamic limits differ. We split a CE with a large volume into a cluster, which is a grand canonical ensemble with the rest of the system being a reservoir [32]. The multiplicity distribution in a cluster is given by a negative binomial distribution (NBD)⁴ while the rest (reservoir), treated as a superposition of elementary collisions, is described by a binomial distribution (BD).⁵ The variance of a multiplicity distribution, $\text {Var}\left( N\right)$, depends on the mean multiplicity $\langle N\rangle$ of the system. If $\langle N\rangle$ increases with energy, $\text {Var}\left( N\right)$ also changes.

Figure 1 presents a compilation of values of scaled variances of the charged particle multiplicity distributions as a function of the average charged multiplicity. Such a dependence may be well fitted by a simple formula⁶:

$$\begin{aligned} \omega \left( N\right) =0.058\cdot \langle N\rangle ^{1.5}. \end{aligned}$$

(5)

Comparing multiplicity fluctuations in jets and in minimum bias proton–proton interactions one observes a kind of self-similarity of the multiparticle production processes [39]. Regardless of the amount of the available energy, the variance is described by the same power function of the average multiplicity.

Fig. 3

Average number of all charged particles (panel a)) and scaled variance of all charged multiplicity distribution (panel b)) of particles produced in Pb+Pb collisions at $\sqrt{s_{NN}}=17.3$ GeV and recorded in the $1.1< y_{\pi } < 2.6$ pion rapidity interval in the center of mass frame, plotted as a function of the number of nucleons from the projectile nucleus which participate in the collision. Circles are for NA49 data [13]

Fig. 4

The same as in Fig. 3 but for negatively charged particles

A negative binomial distribution is a statistical tool commonly used for the description of the multiplicity distributions of particles produced in high-energy nuclear collisions:

$$\begin{aligned}&P_\text {NBD}\left( N,\langle N\rangle ,k\right) \nonumber \\&\quad =\left( {\begin{array}{c}N+k-1\\ N\end{array}}\right) \left( \frac{\langle N\rangle }{k}\right) ^{N}\left( 1+\frac{\langle N\rangle }{k}\right) ^{-N-k}. \end{aligned}$$

(6)

NBD has two free parameters: $\langle N\rangle$ describing mean multiplicity and the, not necessarily integer, parameter k ($k\ge 1$) affecting the shape of the distribution. The variance of NBD is given by

$$\begin{aligned} \text {Var}\left( N\right) =\langle N\rangle +\frac{\langle N\rangle ^{2}}{k}. \end{aligned}$$

(7)

Both $\langle N\rangle$ and k depend on the collision energy. The energy dependence of the average multiplicity of the charged particles produced in proton–proton interactions may be well parameterized by [34]

$$\begin{aligned} \langle N_\text {ch}\rangle =A + B\ln s + C\ln ^{2} s, \end{aligned}$$

(8)

where $\sqrt{s}$ is the center of mass energy of two colliding protons, and $A=2.7\pm 0.7$, $B=-0.03\pm 0.21$, and $C=0.167\pm 0.016$. The parameterization (8) is valid for $\sqrt{s}$ ranging between 10 and 900 GeV. In proton–proton collisions the energy dependence of the NBD shape parameter k is given by [34]

$$\begin{aligned} k^{-1}=a + b\ln \sqrt{s}, \end{aligned}$$

(9)

with $a=-0.104\pm 0.004$, $b=0.058\pm 0.001$, and s in $\text {GeV}^2$. Using Eqs. (8) and (9) one can obtain a NBD shape parameter k as a function of the average charged multiplicity, $\langle N_\text {ch}\rangle$:

$$\begin{aligned}&{k^{-1}\left( \langle N_\text {ch}\rangle \right) }\nonumber \\&= -0.104+0.0868\left( 0.03+\sqrt{-1.8+0.668\cdot \langle N_\text {ch}\rangle }\right) .\nonumber \\ \end{aligned}$$

(10)

Using Eq. (8) one may also find that at the center of mass energy of interest, $\sqrt{s}=17.3$ GeV,

$$\begin{aligned} \langle N_\text {ch}\rangle \left( \sqrt{s}=17.3 \mathrm{GeV}\right) =7.95. \end{aligned}$$

(11)

To describe the NA49 data the following particle clusterization method was used. Each projectile nucleon participating in a collision “produces” particles independently,

$$\begin{aligned} \langle N\rangle =N_p\cdot \langle N_\text {ch}\rangle , \end{aligned}$$

(12)

where $\langle N\rangle$ is the average multiplicity produced in Pb+Pb collisions at a particular centrality, $N_{p}$, is the number of nucleons from a projectile nucleus participating in collision and $\langle N_\text {ch}\rangle$ is the average multiplicity produced in proton–proton interactions. Clusters of the secondary particles may be formed up to a certain value of $N_{p}=N_{p}^\text {max}$. The value of $N_{p}^\text {max}$ is sampled from a gamma distribution with $\langle N_{p}^\text {max}\rangle =18$ and $\text {Var}\left( N_{p}^\text {max}\right) =9\cdot \langle N_{p}^\text {max}\rangle$; see Fig. 2. The cluster size is equal to $N_{p}^{C}=\text {min}\{N_{p},N_{p}^\text {max}\}$. Having $\langle N\rangle =N_{p}^{C}\langle N_\text {ch}\rangle$, the multiplicity in a given cluster is calculated according to NBD ⁷ with the shape parameter k dependent on $\langle N\rangle$, according to Eq. (10).

Fig. 5

Scaled variance of negatively charged multiplicity distribution of particles produced in p+p and the most central (1%) Be+Be, Ar+Sc and Pb+Pb collisions, and emitted to the forward hemisphere, $y_{\pi }>0$ plotted as a function of the number of nucleons from the projectile nucleus which participate in the collision. Symbols present data of the NA49 and NA61/SHINE experiments [14, 15]. With the line we show values obtained using our model

The rest of the colliding projectile nucleons, $m=N_{p}-N_{p}^\text {max}$ do not contribute their produced particles to the cluster. The particles produced by them are emitted according to a binomial distribution:

$$\begin{aligned} P_\text {BD}\left( N, n, p\right) =\left( {\begin{array}{c}n\\ N\end{array}}\right) p^{N}\left( 1-p\right) ^{n-N}, \end{aligned}$$

(13)

with $\langle N\rangle =\langle N_\text {ch}\rangle$, and probability $p=p_\text {BD}=0.4$.

Clusters of particles are formed with a certain probability, $p_{C}=0.25$. If a cluster of particles is not formed then all colliding nucleons emit their produced particles according to a binomial distribution.

4 Results

For the simulation of nucleus–nucleus collisions in the framework of the Glauber Monte Carlo picture, we have used a suitably modified GLISSANDO package [42, 43]. The parameters of the particle production were adjusted by fitting of the experimental data.

The resultant centrality dependencies of average all charged multiplicities and corresponding scaled variances of the multiplicity distributions are presented in Fig. 3. To include the experimental acceptance we accepted a fraction of 17% of generated particles; see the appendix for a detailed discussion of the acceptance.

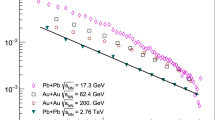
Figure 4 shows similar results to Fig. 3 but for negatively charged particles. To obtain the corresponding fits we had to adjust only one parameter: the average multiplicity in proton–proton collisions. For the case of negatively charged particles $\langle N_\text {ch}\rangle =3.6$. The only difference between the scaled variances for negatively and all charged particles comes from the number of accepted particles. The two-particle correlation function [44]

$$\begin{aligned} \langle \nu _{2}\rangle =\frac{\omega \left( N\right) -1}{\langle N\rangle }, \end{aligned}$$

(14)

which is not dependent on the experimental acceptance, is roughly the same in both cases.

Using similar considerations we have obtained the values for the scaled variance of negatively charged multiplicity distribution produced in p+p and the most central (1%) Be+Be, Ar+Sc and Pb+Pb collisions, and emitted to the forward hemisphere, $y_{\pi }>0$ [14, 15]; see Fig. 5. Nevertheless the NA61/SHINE Collaboration experimental data are still preliminary, and our model describes most of them (except Ar+Sc collisions) quite reasonably. The observed difference for the colliding system as regards size being comparable to the cluster’s size can be caused by a too rough approximation of the cluster size distribution adopted in the model.

5 Concluding remarks

In this paper we used the concept of clusterization in the mechanism of multiparticle production for the description of multiplicity fluctuations observed in relativistic ion collisions at CERN SPS. Our results are as follows:

• It is shown that the observed non-monotonic behavior of the scaled variance of the multiplicity distribution as a function of collision centrality can be fully explained by the correlations between produced particles promoting cluster formation (such an effect is not observed in the widely used string-hadronic models of nuclear collisions).

• We defined a cluster as a quasi-neutral gas of charged and neutral particles which exhibits collective behavior. The characteristic space scale of this shielding is the Debye length.

• We split a canonical ensemble or a micro canonical ensemble with a very large volume into a cluster, which is by definition, a grand canonical ensemble, with the rest of the system acting as a reservoir. The multiplicity distribution in a cluster is given by a negative binomial distribution, while the rest (reservoir), treated as a superposition of elementary collisions, is described by a binomial distribution.

• Multiplicity clustering (being some kind of implementation of the core–corona model [45, 46]) with self-similar fluctuations (power-law dependence given by Eq. (5) obeys the scaling relationship $\text {Var}\left( N;\lambda \langle N\rangle \right) =\lambda ^{2.5}\text {Var}\left( N;\langle N\rangle \right)$) provides new insights on the non-monotonic behavior of multiplicity fluctuations.

Appendix A: Imprints of acceptance

Let us assume that $g\left( M\right)$ presents a real distribution which describe s the multiplicity distribution in the full phase space. The scaled variance $\omega$ is given by the parameters of such a distribution. For example

$$\begin{aligned} \omega = {\left\{ \begin{array}{ll} 1+\langle M\rangle / k &{} \text {for NBD}, \\ 1 &{} \text {for PD } \\ 1-\langle M\rangle /k &{} \text {for BD}. \end{array}\right. } \end{aligned}$$

(A.1)

However, in the experiment we measure the multiplicity only within some window in rapidity, $\Delta y$. Roughly, for a fixed acceptance $\alpha <1$, we have

$$\begin{aligned} \omega = \alpha \cdot \omega _{\alpha =1}, \end{aligned}$$

(A.2)

and the scaled variance decreases monotonically with decreasing acceptance. Of course, such a procedure is not correct. Let us assume that the detection process is a Bernoulli process described by the BD with the generating function

$$\begin{aligned} F\left( z\right) =1-\alpha +\alpha \cdot z, \end{aligned}$$

(A.3)

where $\alpha$ denotes the probability of the detection of a particle in the rapidity window. The number of registered particles is

$$\begin{aligned} N=\sum _{i=1}^{M} n_{i}, \end{aligned}$$

(A.4)

where $n_{i}$ follows the BD with the generating function $F\left( z\right)$ and M comes from $g\left( M\right)$ with the generating function $G\left( z\right)$. The measured multiplicity distribution $P\left( N\right)$ is therefore given by the generating function

$$\begin{aligned} H\left( z\right) =G\left[ F\left( z\right) \right] \end{aligned}$$

(A.5)

and finally we have

$$\begin{aligned} P\left( N\right) =\frac{1}{N!}\frac{d^{N}H\left( z\right) }{dz^{N}}\Biggl \vert _{z=0}. \end{aligned}$$

(A.6)

Note that such a procedure applied to NBD, PD or BD with generating functions

$$\begin{aligned} G\left( z\right) = {\left\{ \begin{array}{ll} \left[ \left( 1-p\right) /\left( 1-pz\right) \right] ^{k} &{} \text {for NBD}, \\ \exp \left[ \lambda \left( z-1\right) \right] &{} \text {for PD, } \\ \left[ 1+p\left( z-1\right) \right] ^{k} &{} \text {for BD}, \end{array}\right. } \end{aligned}$$

(A.7)

gives again the same distributions but with modified parameters. The scaled variance is given by

$$\begin{aligned} \omega = {\left\{ \begin{array}{ll} 1+\alpha \langle M\rangle / k = 1+\langle N\rangle / k&{} \text {for NBD} , \\ 1 &{} \text {for PD } \\ 1-\alpha \langle M\rangle /k = 1-\langle N\rangle /k &{} \text {for BD}. \end{array}\right. } \end{aligned}$$

(A.8)

For all distributions occurring in Eq. (A.8) $\omega \rightarrow 1$ when $\alpha \rightarrow 0$. In the case of a small acceptance, the observed $P\left( N\right)$ tends to PD.

The procedure discussed above is also very rough, because it neglects conservation constraints, e.g., energy conservation. To investigate this effect we adopt an induced partition scenario for the particle distribution in phase space [47]. Namely, if the available energy, which may be distributed among secondary particles $U=const$ is limited, then we have the following conditional probability for the single-particle energy distribution [47]:

$$\begin{aligned} f\left( E|U\right)= & {} \frac{f_{1}\left( E\right) \cdot f_{N-1}\left( U-E\right) }{f_{N}\left( U\right) }\nonumber \\= & {} \frac{N-1}{U}\left( 1-\frac{E}{U}\right) ^{N-2}. \end{aligned}$$

(A.9)

In the induced partition mechanism $N-1$ randomly chosen independent points $\{U_{1},\,\ldots ,\,U_{N-1}\}$ split a segment (0, U) into N parts, whose length is distributed according to Eq. (A.9). The length of the kth part corresponds to the value of energy $E_{k}=U_{k+1}-U_{k}$ (for ordered $U_{k}$). In our example it could correspond to the case of random breaks of a string in $N-1$ points in the energy space [47].

To check the above considerations numerically let us take as an example a constant energy $U=100$ GeV and share it between a constant number, $N=50$ massless particles using the induced partition mechanism. Then we split the generated particles into two different multiplicity distributions, $P1\left( N\right)$ and $P2\left( N\right)$. If the energy of the secondary particle is smaller than the energy $E_{t}=0.38$ GeV then we put this particle into the distribution $P1\left( N\right)$. Otherwise the particles will populate the distribution $P2\left( N\right)$. In such a way we put into the multiplicity distribution $P1\left( N\right)$ about 17% of thr particles. In Fig. 6 we show both distributions, $P1\left( N\right)$ and $P2\left( N\right)$. Please note that the two $P1\left( N\right)$ and $P2\left( N\right)$ multiplicity distributions have exactly the same variances. Moreover, Pearson’s correlation coefficient calculated for distributions $P1\left( N\right)$ and $P2\left( N\right)$,

$$\begin{aligned} \rho \left( N_{P1},N_{P2}\right) =\frac{\langle N_{P1}\cdot N_{P2}\rangle -\langle N_{P1}\rangle \cdot \langle N_{P2}\rangle }{\sqrt{\text {Var}\left( N_{P1}\right) \cdot \text {Var}\left( N_{P2}\right) }} , \end{aligned}$$

(A.10)

equals $\rho \left( N_{P1},N_{P2}\right) =-1$. The multiplicity distribution $P1\left( N\right)$ may be easily fitted by a BD, Eq. (13) with parameters $n=27.4$ and $p=0.31$; see Fig. 6.

Fig. 6

The left histogram shows multiplicity distribution $P1\left( N\right)$ of 17% least energetic particles from the original number of 50, $U=100$ GeV. A red line shows our BD fit. The right histogram presents the multiplicity distribution $P2\left( N\right)$ of the remaining 83% of particles. See text for details

Fig. 7

$\omega _{\alpha }$ as a function of $\omega =\omega _{\alpha =1}$ for $P\left( M\right)$ given by BD, PD and NBD, with $\alpha =0.15$ and $z=2$. The results obtained for $\langle M\rangle =30$ and $\langle M\rangle =50$. See text for details

The “measured” multiplicity distribution is given by

$$\begin{aligned} P\left( N\right) =\sum _{M=N}^{\infty } P\left( M\right) \cdot P\left( N|M\right) . \end{aligned}$$

(A.11)

From the induced particle scenario we have the acceptance function:

$$\begin{aligned}&P\left( N|M\right) \nonumber \\&=\frac{\Gamma \left( M/z+1\right) }{\Gamma \left( N+1\right) \cdot \Gamma \left( M/z-N+1\right) }\left( z\alpha \right) ^{N}\left( 1-z\alpha \right) ^{M/z-N}, \nonumber \\ \end{aligned}$$

(A.12)

where z is a parameter and $\alpha$ is the acceptance.

Contrary to the previous results given in Eq. (A.8), the consideration of energy conservation leads to the apparent changes in the “measured” multiplicity distribution. As an example in Fig. 7 we plot $\omega _{\alpha }$ as a function of $\omega =\omega _{\alpha =1}$ for $P\left( M\right)$ given by BD, PD and NBD, with $\alpha =0.15$ and $z=2$. The scaled variance $\omega _{\alpha }=1-\alpha$ for PD and reaches the value $\omega _{\alpha }=1$ for NBD with $\omega =2$. For NBD we have $\omega _{\alpha } < \omega _{\alpha =1}$ and for BD $1-z\alpha \le \omega _{\alpha } < 1-\alpha$. Such a behavior is almost insensitive to $\langle M\rangle$; see Fig. 7.