INTRODUCTION

Among the most important elements of the probable earthquake forecast are short-term earthquake precursors. This problem has been extensively addressed in the literature (Gokhberg et al., 1985; Sobolev and Lyubushin, 2006; Peresan et al., 2015). An important role in recording short-term precursors of significant seismic events with magnitudes М > 6 is played by satellite-based methods capable of revealing anomalies of geophysical fields over large territories, including the geodynamic anomalies which manifest themselves in the deformation of lineament systems (Bondur and Zverev, 2005a; 2005b; 2007) and surface displacements (Cenni et al., 2015), variations in the ionospheric parameters (Bondur and Smirnov, 2005; Bondur et al., 2007), thermal anomalies (Ouzounov et al., 2007), and other phenomena arising at the preparatory stages and during the seismic event itself. At the same time, forecasting is mainly challenged by the absence of reliable short-term precursors (Geller, 1997; Koronovskii et al., 2019).

Bondur et al. (2020c) associate one of the probable sources of these difficulties with the fact that deformation-related anomalies in various parameters at the preparatory stage of an earthquake are confined to the deep layers of the Earth’s crust which concentrate all of seismicity, whereas the surface manifestations are substantially weaker. A probable solution is proposed based on geomechanical model iteratively updated with local seismicity data.

The geomechanical model of Southern California developed in (Bondur et al., 2007; 2010; 2017) allows for monitoring the stress-strain state (SSS) dynamics based on local current seismicity data (USGS catalog https://earthquake.usgs.gov/data/comcat/) and revealing the short-term precursors of the strong earthquakes (Bondur et al., 2020a; 2020c; 2021). Most informative deformational variations are observed in the increments of shear deformation (SD) and from parameter D reflecting the proximity of rocks to the ultimate strength, which are calculated in the model with a time step of 0.5 months. The term “shear deformation” used in this work refers to the increments of shear deformation rather than to the absolute deformation ​​figures accumulated over the entire period of geomechanical monitoring.

In (Bondur et al., 2016), it is shown that there is a large-scale interaction between the tectonically different provinces of Southern California—the northern and southern ones, having their boundary at approximately 34° N. The northern province has a fairly complex structure associated with the junction of the San Andreas fault and sub-latitudinal Garlock and Mount faults, whereas the relatively simple structure of the southern province is determined by the San Andreas fault. It is shown that when elevated shear deformation is observed in the northern province, stress-strain anomalies in the southern province are practically absent. On the other hand, in the absence of SD in the northern province, stresses in the south begin sharply build up, and the rocks in the crust become maximally proximate to the ultimate strength.

This work continues the study of interactions the dynamics of deformation process on a more detailed basis and limitied to specific local subdomains of the geomechanical model. The 2019 Ridgecrest earthquake with М = 7.1 occurred in the tectonically complex northern province, in contrast to the 2010 Baja California earthquake with M = 7.2. In (Bondur et al., 2021) it was shown that for a more efficient way to identify a short-term precursor of this event is to analyze the stress-strain state (SSS) dynamics in a local subdomain of the model of northern province in direct vicinity of the epicenter. This will be the basis of the discussion focused on the results below.

STRESS-STRAIN STATE ANOMALIES IN 2016–2019

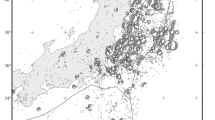
In this work, the detailed spatial features and interactions of the SSS dynamics are studied in the modeling area divided into 25 subdomains, from A1 to E5 (Fig. 1). Each ~100 × 100 km subdomain contains 400 model cells (meshes) with a size of 5 × 5 km. The epicentral zone (EZ) of the Ridgecrest earthquake of July 6, 2019 falls in subdomain C1.

Fig. 1.
figure 1

Partition of modeling region for Southern California into subdomains. Gray shades show initial damage distribution associated with fault tectonics. Region inside oval corresponds to ground shaking intensity 6–8. Asterisk marks earthquake epicenter, black line shows approximate dimensions and orientation of rupture surface.

Full size image

Figures 2a, 2b show the graphs of the maximum increments of shear deformations (SD) with a half-month time step in subdomains C1 and B2 from November 2012 to August 2019. The graph of parameter D (to the ultimate strength) in the second layer of the upper crust (3–7 km) accommodating almost all of the seismicity of the study region is shown in Fig. 2c for the subdomain C1 in the interval from May 1, 2016 to August 1, 2019. Starting from May 2016, a number of the characteristic time intervals of quiescence appear, during which significant shear deformations are absent and rocks are maximally distant from the ultimate strength. This situation is mainly observed in the EZ in the C1, and, to a lesser extent, also in D1, D2, and B1. At the same time, at a larger distance from EZ in other (B2, C3, D3, C4, D4), these characteristic quiescence episodes are absent and, instead, continuous SD variations are observed (Fig. 2b). In other, SD manifestations are either feeble or abscent.

Fig. 2.
figure 2

Variations in SSS parameters based on geomechanical modeling results: (a) graphs of maximum shear deformations (SD) in C1 (EZ) subdomain. Numerals in upper part indicate excursions numbers; (b) graphs of maximum shear deformations (SD) in B2 window; (c) variations of maximum in parameter D in C1 (EZ). Black asterisks show earthquakes with M > 5 that occurred within modeling area.

Full size image

Thus, approximately three years prior to the analyzed seismic event, successive alternations of the periods of quiescence (SD are absent, rocks are far from the ultimate strength) and sharp increases in the SD amplitude with closest possible approach of rock state to the ultimate strength are detected in the EZ region. These processes in the zone of preparation of the earthquake can be called SSS excursions when after a quiet period, the rocks maximally closely approach the ultimate strength and experience substantial shear deformations, which, however, does not result in a catastrophic event but is subsequently followed by the next relaxation cycle (a return to the next quiescence).

Five excursions can be distinguished before the Ridgecrest earthquake. These excursions are indicated in Fig. 2 by numbers and analyzed below. The analysis considers SD variations in model subdomains and focuses on the regularities in the spatial distribution of SSS during the quiescence periods and subsequent bursts of activity, which is an important link in understanding the earthquake preparation process. The series of Figs. 3–8 schematically shows the contours of SD anomalies in the upper crustal layer 2 at a depth of 3–7 km for a number of the characteristic quiescence episodes beyond EZ and during the subsequent SD maxima within EZ.

Fig. 3.
figure 3

Excursion 1. Contours of shear deformation (SD) anomalies: (a) quiescence, May 2016 (solid isoline at 1.0 × 10–4, dashed isolines at 2.0 × 10–4, maximum 3.0 × 10–4 in C2); (b) SD anomaly on July 1, 2016 (solid isoline at 2.6 × 10–4, dashed isoline at 4.0 × 10–4, maximum 5.2 × 10–4).

Full size image
Fig. 4.
figure 4

Excursion 2. Contours of shear deformation anomalies (SD): (a) quiescence, February 2017 (solid isoline 2.0 × 10–4, dashed isoline 1.5 × 10–4, maximum 4.0 × 10–4 in the B2 in southwest); (b) SD anomaly on July 1, 2017 (solid isoline at 1.5 × 10–4, maximum 3.0 × 10–4).

Full size image
Fig. 5.
figure 5

Excursion 3. Contours of shear deformation (SD) anomalies: (a) quiescence on February 1, 2018 (solid isoline at 1 × 10–4, maximum 2 × 10–4 in С2 in south); (b) SD anomaly on March 15, 2018 (solid isoline at 1.4 × 10–4, maximum 2.8 × 10–4 in C1 in EZ, dashed line at 2.0 × 10–4).

Full size image
Fig. 6.
figure 6

Excursion 4. Contours of shear deformation (SD) anomalies: (a) quiescence, August 15, 2018 (solid isoline at 1 × 10–4; maxima 2.7 × 10–4 in B1 to west, 2.0 × 10–4 in D5 to southeast, 1.6 × 10–4 in D1 to east); (b) SD amplitude of September 1, 2018, 2.2 × 10–4 (solid isoline at 1 × 10–4, maxima 2.2 × 10–4 in C1 and C2 to south, 1.8 × 10–4 in B5, C5, D5 in south).

Full size image
Fig. 7.
figure 7

Excursion 5. Contours of shear deformation (SD) anomalies: (a) SD quiescence on March 1, 2019 (solid isoline at 1 × 10–4, maxima 1.6 × 10–4 in A2, B2 to southwest, 1.7 × 10 –4 in С5, D5 to south and southeast); (b) SD amplitude as of May 1, 2019 (solid isoline at 0.5 × 10–4, maxima: 1.3 × 10–4 in A1 to west, 1.0 × 10–4 in C3, D5 to south and southeast).

Full size image
Fig. 8.
figure 8

Contours of shear deformation (SD) anomalies for last quiescence before event: (a) quiescence on June 15, 2019 (solid isoline at 1 × 10–4, maxima 2.3 × 10–4 in B2 in southwest and in D5 in southeast); (b) quiescence on July 1, 2019 (solid isoline at 1 × 10–4, dashed line at 2 × 10–4, maxima 3 × 10–4 in D2 in southeast and 2 × 10–4 in B2 in southwest, 2.7 × 10–4 in D5 in southeast).

Full size image

Excursion 1. Before this excursion, starting from November 2012, the amplitude of SD variations persists at the level 1 × 10–4. After a certain decrease from November 2014 to March 2015, the amplitude of the variations increases but quiescence is not observed.

Figure 3a shows the spatial distribution of the SD increment during the quiescence period in May 2016. The zone of maximum SD (C2 with a maximum of 3 × 10–4) is localized in the immediate southern vicinity of the quiescence region in the epicentral zone (EZ, marked with asterisk) in C1. After this quiescence, the SD amplitude in the EZ sharply increases to 5.2 × 10–4 (highest SD value over the entire period). From Fig. 3b it can be seen that the zone of maximum SD is concentrated strictly within the EZ (C1) with a steep decrease at isoline 2.6 × 10–4. Excursion 1 is the maximum excursion in EZ in terms of the SD amplitude and spatial concentration.

Excursion 2. The anomalous, longest quiescence in shear deformations and parameter D lasts for ~8 months from October–November 2016 to May–June 2017 (Figs. 2a, 2c). Figure 4a shows the SD spatial distribution for the time interval in February 2017 when the maximum amplitudes 4 × 10–4 are observed beyond the quiet zone. It can be seen that the region of ​​maximum SD is localized in the immediate southwestern vicinity of EZ with isoline 2 × 10–4. During such a long quiescence, the EZ rocks, generally speaking, should experience a fairly strong impact from the nearby SD. As a result of this action, in July 2017, rocks in the EZ steeply approach the ultimate strength and become affected by significant SD over a shortest-possible time interval of 0.5 months (Fig. 2a).

Figure 4b shows the spatial distribution of SD during the maximum EZ activation on July 1, 2017. It can be seen that the SD intensity increase is only observed in EZ with a maximum at 2.8 × 10–4 rapidly decaying decrease in the surrounding area at the level of isoline 1.7 × 10–4. The EZ appears to be close to the event; however, the earthquake did not occur, and a new period of quiescence started at the beginning of 2018 (Fig. 2a). This behavior repeated three times again up to the very Ridgecrest earthquake of July 6, 2019.

Excursion 3. Figure5a shows a similar SD distribution for the quiescence period on February 1, 2018. The maximum SD (2 × 10–4) is located south of EZ in the immediate vicinity of it (subdomain C2). From Fig. 5b it can be seen that a sharp increase in the SD amplitude to 2.8 × 10–4 mainly falls in EZ. At the same time, a weak maximum 1.7 × 10–4 arises southeast of the EZ on the San Andreas Fault in subdomains D3, D4.

Excursion 4. SD maxima on August 1, 2018 are located around the quiet zone in the EZ (1.2 × 10–4 west of EZ in B1, 1.6 × 10–4 east of EZ in D1, and 1.7 × 10–4 southeast of EZ along the San Andreas fault in D5).

The positions of the SD maxima around the continuing quiescence zone on August 15, 2018 are shown in Fig. 6a and prove to be similar to the previous distribution, with relatively larger amplitudes. The distribution of the anomalous increase in the SD amplitude after the quiescence is illustrated in Fig. 6b. Besides the maximum in EZ (2.2 × 10–4), there is also a maximum 1.8 × 10–4 observed south of EZ in B5, C5, D5. Thus, in Excursion 4, spatial expansion of both the SD zone around the quiescence and the SD maximum itself is observed.

Excursion 5. During the quiescence period of March 1, 2019, two maxima appear southwest of EZ in A2, B2 (1.6 × 10–4) and southeast of EZ at the southern end of the San Andreas fault in C5, D5 (Fig. 7a). Despite the relatively low amplitude 1 × 10–4, the last SD burst before the Ridgecrest earthquake described in (Bondur et al., 2020b; 2020c) has the largest spatial dimensions. Besides the peak in EZ, SD intensity increase is observed along the entire length of the San Andreas fault from A1 to E5 (Fig. 7b; a similar behavior is also the case during the preparation of the Baja California earthquake of 2010).

Such extended regions of SD activation correspond to the size of the preparation zone of an earthquake with М = 7.

During the quiescence immediately before the event—on June 15, 2019 and July 1, 2019, the SD anomalies around EZ had large amplitudes (2–3 × 10–4) and a significantly transformed spatial distribution. During the quiescence of June 15, 2019 (Fig. 8a), the SD anomalous zone in the model spans the entire length of the San Andreas Fault and has the maxima with amplitudes of 2.7 × 10–4 and 2 × 10–4 in the southeastern and northwestern ends of the fault, respectively. On July 1, 2019 (Fig. 8b), i.e., five days before the event, the configuration of SD spatial distribution changes dramatically.

The maximum with amplitude 3 × 10–4 emerges beyond the San Andreas Fault zone, in fact, on a different (eastern) side of EZ. It suggests that this SD distribution creates perhaps a more efficient impact on EZ than other excursions, which sort of embraces the EZ from all sides. The maximum SD amplitude lies on the continuation of the future earthquake source approximately 100 km off its southeastern end. This is perhaps one of the sought distinctions of the precursor immediately before the event.

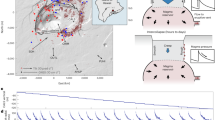
For the quiescence period on July 1, 2019, five days before the event, we calculated the spatial distribution of displacement vector amplitudes and directions in the second crustal layer at a depth of 3–7 km in the region surrounding EZ (Fig. 9b). The maximum displacement amplitude (~0.15 m) in the model is located at distance R ~ 100 km southeast of the EZ. For comparison, in the EZ, we show distributions of surface displacements in the vicinity of the source based on the Sentinel-2 satellite monitoring data (Figs. 9a, 9b) for the period from June 28 to July 8, 2019 (Chen et al., 2020). The maximum displacement in the source is estimated at 1.6 m.

Fig. 9.
figure 9

(a) Surface displacement map in the region of Ridgecrest earthquakes from (Chen et al., 2020) based on Sentinel-2 satellite monitoring data for the period from June 28, 2019 to July 8, 2019; (b) comparison of displacements at a depth of 3–7 km calculated in model five days before event and source displacements estimated from Sentinel-2 satellite images.

Full size image

The displacement in the source is noted in a direction from the northwest to the southeast (reddish area) along the northeastern side of the rupture and from the southeast to the northwest along the southeastern side (bluish area). This distribution of the displacement directions is consistent with the results of geomechanical modeling in the immediate vicinity of the southeastern termination of the source during the last quiescence before the event.

Thus, during the last period of quiescence five days before the event, there has been certain consistency both in the displacement directions and distributions of SD amplitude between the region surrounding the EZ at the depths of the second crustal layer and the future earthquake source (estimated from surface displacements based on satellite images).

DISCUSSION

Part 1

We have analyzed the series of the successive SSS excursions over a period of about three years preceding the Ridgecrest event of 2019 starting from May 2016. It is shown that in each excursion, during the quiescence period, SD maxima emerge in the vicinity of EZ and their spatial distribution changes during the preparation of the earthquake.

Initially (excursions 1, 2, 3), the increase in SD intensity is local both within and beyond the EZ. During the quiescence period, the regions of maximum SD are mainly clustered in the immediate vicinity south and southwest of the EZ.

Starting from August 1, 2018 (excursion 4), one year before the event, the SD activation region during the quiescence period expands around EZ in the form of isolated maxima in the west, east, and southeast; besides the increase in the SD amplitude within the EZ, an additional maximum appears south of EZ.

The expansion of the SD region reaches maximum during the last excursion 5 before the event, on June 15, 2019. Here, the SD anomaly covers almost the entire length of the San Andreas Fault in the model, which corresponds to the dimensions of the preparation zone of an earthquake.

During the last quiescence on July 1, 2019, five days before the event, the SD anomaly again begins clustering in the immediate vicinity of EZ, enveloping it from all sides. Here, in contrast to the previous distributions, the maximum in the amplitude is located in the immediate southeastern vicinity of EZ. Thus, in the process of successive alternation of the excursions, the anomalous SD regions gradually expand outside the EZ during quiet periods and during SD bursts following the quiescence.

The Ridgecrest earthquake of July 6, 2019 occurs after the last sixth quiescence episode, when the zone of the anomalous SD encompasses the EZ from all sides, with the maximum effect observed in the EZ immediate southeastern vicinity.

Remarkably, despite the fact that the Ridgecrest earthquake occurred in the vicinity of the Garlock Fault, the San Andreas Fault plays important role throughout the entire preparation process. As can be seen in Figs. 7b and 8, with approaching the event, the entire San Andreas Fault zone experiences anomalous SD.

Thus, we may probably state that based on the calculations of stress-strain state dynamics in the geomechanical model of Southern California, we have revealed early manifestations of the short-term precursors in the form of the successively alternating periods of SD quiescence with maximum remoteness of EZ rocks from limiting strength in terms of parameter D (strengthening) and SD bursts when rocks approach limiting strength in terms of parameter D.

It is worth noting that based on these results, it is possible to calculate the loads under the action of SDs surrounding the EZ during the quiescence periods; however, this is beyond the scope of this work.

It seems not impossible that multiple periods of quiescence were precursory to the so called slow earthquakes. Such earthquakes lasting for about weeks or months without the release of seismic energy were previously detected by American geophysicists on the San Andreas Fault (Linde et al., 1996). Silent earthquakes can cause many small earthquakes, which, in turn, prepare the conditions for a more catastrophic event.

The successive emergence of SD maxima in the region surrounding EZ during quiescence followed by the anomalous bursts in SD amplitude directly within the EZ against the absence of such bursts beyond EZ corresponds to the situation of the so-called swing. The SD anomalies alternately display within the EZ and in the surrounding region (SR) at distances on the order of 100–400 km with periods T ~1–8 months corresponding to the times of the excursions. The amplitude in each swing cycle varies by more than an order of magnitude, from 10–5 to 5 × 10–4.

During the period of excursions which spans three years before the event, the entire region of earthquake preparation seems to be swinging as demonstrated in Fig. 10.

Fig. 10.
figure 10

Schematic model of swinging of Ridgecrest earthquake preparation zone there years before event. Distance R is ~100–400 km, swing period T is 1 to 8 months, amplitude of deformation variations is from 1 × 10–5 to 5 × 10–4, swing cycle duration is ~3 years.

Full size image

Generally speaking, in the context of this swing model, we can assume in a short-term forecast that a process associated with the triggerring of the event had begun. The particular cycle of swinging which contains the earthquake event remains unclear in the scope of this analysis unless the reliable distinctive features of the excursions in their sequence are found. In this situation, important focus is studying the spatiotemporal distribution of the displacement vectors shown in Fig. 9 which, as being a new parameter, may help establishing the differences at different stages of swinging.

Part 2

The formation of a quiescence zone before an earthquake can be explained based on the well-known models of earthquake preparation—the dilatancy-diffusion model (DD-model) (Nur, 1972; Whitcomb et al., 1973; Scholz et al., 1973; Rice, 1975) and the avalanche unstable fracture formation model (AUF) (Myachkin et al., 1974; 1975).

Inelastic deformation of the Earth’s crust at the approach to the ultimate strength is accompanied by dilatancy—an increase in the volume of fractured rock (Nikolaevskii, 1971). As a result of crack opening, pore pressure in a rock drops and effective normal stresses increase leading to the dilatant strengthening of the rock mass in the source (the quiescence zones in EZ-c1) relative to the continuing deformation (zones around the C1 subdomain during the quiescence period). Subsequently, as the pore pressure is back to normal, effective stresses decrease and cracking resumes leading to weakening of the material. This is expressed in the fact that the process follows the descending branch of the deformation diagram. The quantitative analysis carried out in (Rice, 1975) has shown that in this case, dilatant strengthening becomes unstable in the region of negative plastic moduli.

After the peak stress is reached, the pattern of crack distribution changes noticeably. The partial closure of some defects and accelerated growth of others forms a predominant defect orientation, which leads to material weakening. This is expressed in that the deformation process implements the descending branch of the deformation diagram and the material passes to a state of rheological instability (Garagash and Nikolaevskii, 1989). This is accompanied by the formation of narrow crack-like macroscopic deformations linking a large number of microdefects.

These deformations called shear bands are the localization zones of plastic deformation along which ultimate failure of rock material occurs with the release of seismic energy. Figure 11 shows the shear bands formed in sandstone samples under confining pressure (Desrues and Viggiani, 2004). A characteristic feature is that two parallel shear bands were formed at the transition to the descending branch of the deformation diagram at point 5.

Fig. 11.
figure 11

Distributions of (a) shear deformations and (b) bulk deformation corresponding to points 2, 3, 5 and 6 on deformation curve.

Full size image

Thus, the pattern of deformation of the Earth’s crust in the future earthquake source is consistent with the concepts of earthquakes preparation theories and is supported by the experiments with rock samples.

Considering the fact that the analysis in this work is mainly based on the distributions of shear deformations (SD) whose absolute values may differ from the actually measured quantities, below we present some calibration.

The distribution of the calculated monthly shear deformations in the upper layer of the Earth’s crust in Southern California is somewhat higher than the typical average level of deformations measured in nature (Gabsatarov, 2012). This is due to the fact that the values of mechanical parameters of damage and loads specified in the model are rough and, of course, cannot provide complete coincidence of the calculated and observed parameters. Therefore, if we are interested in the absolute values, then the calculated values ​​need to be calibrated. To fit the average level of shear deformations observed in nature, the calculated values ​​should be taken with the coefficient k = 0.3.

CONCLUSIONS

The detailed analysis of the stress-strain state on local segments of the Earth’s crust in the geomechanical model of Southern California before the Ridgecrest М = 7.1 earthquake of July 6, 2019 revealed early manifestations of the short-term precursors which appeared three years before the event.

It is found that directly in the epicentral zone, the months long time intervals with the absence of shear deformations (SD) and maximum remoteness of rocks from the ultimate strength in terms of parameter D successively alternate with the subsequent bursts of SD activity with steep approach of the rocks to the ultimate strength.

Such time intervals are called excursions, and before the studied event there were five such excursions. Excursion 1 (May to August 2016) is the largest in amplitude. The excursions are consistent the existing earthquake preparation theories and, perhaps, are accompanied by slow earthquakes which are observed in California. The detailed analysis of the spatial distribution of SD during the excursions within a quiescence period has shown that around EZ, SD intensity increase takes place at different distances and from different sides, and the dimensions of this activation regions consistently increase when the approach of the moment of the event.

The alternate emergence of shear deformations in the epicentral zone and in the surrounding region corresponds to “swinging” of the preparation area of the Ridgecrest earthquake three years before the event. During the last quiescence five days before the event, the maximal SDs are clustered in the immediate vicinity of EZ with a significantly different configuration of the cluster. A correlation exists between the directions of the displacement vectors at the depth of the second crustal layer and displacements in the source estimated from satellite images of the Earth’s surface.

The load created by the SD impact of the medium around the EZ can be calculated in the model based on the obtained results; however, this is beyond the scope of this work.

The results presented in this work are consistent with theoretical models of earthquake preparation processes. The presence of the revealed excursions can complicate the real short-term forecast by producing false alarms unless new peculiarities of the spatiotemporal SD and D distributions before the event itself are found. More detailed calculations with increments of SSS parameters on shorter time intervals using new parameters will probably help to solve this problem.