Abstract—The spatial distribution of the triggered seismic events in mining conditions in the tectonically loaded rock masses is studied using the example of seismicity in the Khibiny Mountains. It is shown that the distribution of distances from the triggering to triggered events, on average, obeys the power-law with a parameter independent of the magnitude of the triggering event. The model of the maximum distances from a triggering event’s hypocenter to the triggered shocks expected with a given probability is derived. It is shown that the model is consistent with the real data. Based on the error diagram analysis, the guidelines are proposed for the practical use of the model.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
INTRODUCTION
This work continues our research into spatiotemporal patterns of seismicity in mining regions. Conducting our investigation into the subject, we validated the productivity law established in our previous works (Baranov and Shebalin, 2020; Shebalin et al., 2020) for the conditions of mining-induced seismicity by showing that the number of the triggered events shocks initiated by an earlier event (productivity) obeys exponential distribution (Baranov et al., 2020). Here, the single parameter of the exponential distribution is independent of the magnitude of the triggering event.
In this work, by analyzing the seismicity of the Khibiny massif, we show that the distances from the triggered earthquakes to their triggering seismic events obey the power-law distribution. This conclusion is consistent with the well-known results previously obtained for the aftershocks of the tectonic earthquakes in California and Japan (Huc and Main, 2003; Felzer and Brodsky, 2006; Richards-Dinger et al., 2010). The last two cited works reflect the discussion on whether the dynamic stress transfer can induce aftershocks.
Felzer and Brodsky (2006) concluded that the observed power-law distribution of distances between aftershocks and their main shocks agrees with the fact that the probability of the occurrence of the aftershocks is practically proportional to the amplitude of seismic waves. In the cited work it is also shown that this distribution is poorly consistent with the rate-state models describing movements along a fault with friction that depends on the changes in static stress, velocity, and state (Dieterich, 1994; Scholz, 1998). Considering this and the fact that static stress changes at the more distant aftershocks are negligible, Felzer and Brodsky (2006) hypothesized that aftershocks can be initiated by the dynamic stress transfer from the main shock. Subsequently, Richards-Dinger et al. (2010) used the algorithm of (Felzer and Brodsky, 2006) to identify the main shocks and aftershocks and have shown that the power-law decay of the density of the repeated shocks with distance is also observed for the aftershocks that occurred before the arrival of seismic wave from the main shock, which violates causality in the case of the dynamic stress transfer. Thus, the power-law decay of aftershock density with distance does not signify that dynamic stress transfer causes repeated shocks.
In our opinion, there are also no grounds to believe that the power-law character of spatial distribution of the aftershocks indicates their initiation by the dynamic stress transfer from the main shock because the same distribution is also observed for the distances between earthquake pairs (no matter whether they are main shocks or aftershocks) on the global and regional levels (e.g., (Kagan and Knopoff, 1980; Kagan, 2007 and references therein)) reflecting the fractal geometry of the seismicity. We note that a fractal structure was also obtained for crack distribution observed in the laboratory experiments on fracturing of Oshima granite (Hirata et al., 1987).
This study is relevant for the matter at hand as it confirms that the power-law distribution of distances from main shocks to their aftershocks established for tectonic seismicity with M ≥ 2 is also valid for the weak mining-induced seismicity (0 ≤ M ≤ 3.3, 104 ≤ E ≤ 8.7 × 109 J). This indicates that the power-law character of the spatial distribution of the repeated shocks appears to be universal. At the same time, in order to accept the power-law distribution as valid on all energy scales, it is necessary to carry out laboratory studies similar to those described in (Hirata et al., 1987; Smirnov et al., 2019; 2020; Smirnov and Ponomarev, 2020).
Mineral extraction in the tectonically loaded rock masses causes manmade seismicity (e.g., (Adushkin, 2013; 2016; Kozyrev et al., 2018; Adushkin et al., 2020)). In this case, rock pressure in the underground workings of the operating mines disrupts the continuity of the rock mass including its near-contour part which manifests itself in the dynamic forms as peeling-off and shooting of rocks, dynamic culling, micro-impacts and rock bursts and manmade earthquakes (Kozyrev et al., 2016). Just as the tectonic (natural) seismicity, mining-induced earthquakes can trigger repeated shocks (aftershocks) (Plenkers et al., 2010; Woodward and Wesseloo, 2015; Kozyrev et al., 2018; Baranov et al., 2019a; 2020). After a mining-induced earthquake, a decision should be rapidly made as to suspending the work, evacuating the people, and removing the equipment from the danger zone. Thus, the research addressing spatiotemporal patterns of the postseismic processes in mining regions has a clear practical relevance.
As a practical application of the previously established productivity law for mining-induced seismicity and the power-law spatial distribution of aftershocks revealed in this study, we analytically developed a model that allows for estimating the size of the zone where the triggered events are expected to occur with a given probability. We note that this result is important for safe mining operations.
INITIAL DATA AND IDENTIFICATION OF INDUCED EVENTS
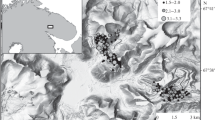
Just as in (Baranov et al., 2020), in this study we use the catalog of seismic events recorded by the seismic monitoring network of the Kirovsk Branch of AO Apatit (Korchak et al., 2014) from 1996 to August 2020 (Fig. 1). The network currently incorporates 50 three-component seismic sensors installed in the Kirovsk and Rasvumchorr mines which record the input signals at a sampling rate of 1000 Hz. The network allows the locations of hypocenters of seismic events with energy E ≥ 104 J to be determined as accurately as up to 25 m in the region of reliable recording. The hypocenter locations of the lower-energy events are estimated less accurately, e.g., the hypocenter location accuracy for the events with E = 103 J is up to 100 m in the region of reliable recording and up to 25 m in the high-accuracy region.
Epicenters of seismic events with 1.5 ≤ M ≤ 3.3 recorded in Khibiny massif from 1996 to August 2020 against terrain relief map. Box in inset shows study region location. Mineral deposits: (1) Kukisvumchorr, (2) Yukspor (mined by Kirovsk mine); (3) Apatite Circus (Rasvumchorr mine); (4) Rasvumchorr Plateau (until 2014 Central mine; currently Vostochnyi mine).
Processing of data of the KB AO Apatit seismic monitoring network includes calculation of event energy E (in J). In this paper, energy was converted into magnitude based on the formula of T.G. Rautian (1960): log E(J) = 1.8M + 4.0.
Since 1996, complete recording of seismic events by the network has been provided starting from energy of Ec = 104 J which corresponds to the magnitude of completeness Mc = 0. The catalog used in our study contains 71 883 seismic events with 0 ≤ M ≤ 3.3. The completeness of the catalog and the accurate, up to 25 m, hypocenter location allow study of very weak seismicity which fills the gap between the laboratory experiments and the field observations. This is an additional test for the universal character of the regularities revealed by both the laboratory studies and the analysis of global and regional catalogs of tectonic earthquakes.
The triggering and triggered events were identified by the nearest neighbor method (Zaliapin and Ben-Zion, 2016) based on the use of the proximity function in the space-time-magnitude region (Baiesi and Paczuski, 2004). This function depends on the parameters of seismicity: the Gutenberg–Richter (GR) b-value and fractal dimension of earthquake hypocenters df. The idea of the method is that for each event in the catalog (except for the first event), we find its “ancestor” determined by the minimum of the proximity function calculated over all the previous events. If the minimum of the proximity function is below a certain threshold η0, the ancestor is assumed a trigger of the analyzed event. Otherwise, the connection between these events is rejected. Here we only consider the highest hierarchy level where the triggering event and its initiated shocks constitute one series. If an initiated shock is itself a trigger, it forms another series. Events that have no triggers are considered background events irrespective of whether they initiate repeated. The η0 value can be selected by various methods, e.g., (Bayliss et al., 2019; Baranov and Shebalin, 2019; Shebalin et al., 2020). Here, we use the model-independent method (Shebalin et al., 2020) which is preferable in the conditions of manmade seismicity (Baranov et al., 2020).
The use of the nearest neighbor method to analyze the seismicity of the Khibiny natural/manmade system (NMS) was discussed in our previous paper (Baranov et al., 2019a; 2020). In the cited work, we obtained the following parameter estimates: b = 1.25, df = 1.55, log η0 = –6.25.
DISTRIBUTION OF DISTANCES FROM THE TRIGGERING EVENTS TO THE TRIGGERED EVENTS
For the triggering seismic events with Mm ≥ 1.5, we construct the distribution of the distances between these events and the triggered shocks with magnitude M ≥ Mm – 1.5 initiated by them. According to (Huc and Main, 2003; Felzer and Brodsky, 2006; Richards-Dinger et al., 2010), distances r between main shocks and their aftershocks starting from certain value r0 obey the power-law distribution
with density
Here, n is the distribution parameter characterizing the slope of the graph plotted on a loglog scale.
It was established that in the case of the seismicity of the Khibiny massif, the distances from the triggering events’ epicenters to triggered shocks starting from r0 = 0.13 km also obey the power-law distribution (Fig. 2) with parameter n = 2.28 in the different ranges of trigger event magnitudes Mm. The standard errors σ (for parameter n) and the r0 values are presented in the caption of Fig. 2, and the characteristics of the series are presented in Table 1. The estimation was carried out by the maximum likelihood method (Clauset et al., 2009). Moreover, just as in (Felzer and Brodsky, 2006), parameter n is independent of the main shock magnitude.
Distribution of epicentral distances from triggering events with different magnitudes Mm to the triggered events with magnitude M ≥ Mm – 1.5. Circles are real values; solid line is approximation by power-law distribution (2) with n = 2.28 ± σ; dashed line corresponds to r0 starting from which distances obey power-law distribution; (a) Mm ≥ 1.5, σ = 0.06, r0 = 0.134 km; (b) Mm ≥ 1.8, σ = 0.10, r0 = 0.130 km; (c) Mm ≥ 2.1, σ = 0.124, r0 = 0.137 km (r0 values are above hypocenter determination accuracy 0.03 km).
The similar result is also valid for vertical (along the depth) distances between the triggering and triggered events (Fig. 3). In this case, we denote the distance in formulas (1) and (2) starting from which the distribution satisfies the power-law by h0. The values of parameter n, standard errors σ, and distance h0 are indicated in the caption of Fig. 3, and the characteristics of the series are presented in Table 1. In the case of vertical (along depth) distances, the scatter in the values of parameter n for different magnitudes is larger than for epicentral distances. This is due to the fact that errors in depth determination are larger than epicenter location errors. Another probable cause is the presence of stress field inhomogeneities along depth increasing the probability that rock pressure manifest itself in the dynamic form (Kozyrev et al., 2019). In turn, these manifestations may lead to the variations in the decay rate of density of the initiated shocks (parameter n). In any case, the ±3σ intervals for the values of n overlap indicating insignificant deviations in the values of this parameter.
Distribution of vertical (along depth) distances from triggering events with different magnitudes Mm to the triggered events with magnitude M ≥ Mm – 1.5. Circles are actual values; circles are real values; solid line is approximation by power-law distribution (2) with parameter n; dashed line corresponds to h0 starting from which vertical (along depth) distances obey power-law distribution. (a) Mm ≥ 1.5, n = 2.29, σ = 0.05, h0 = 0.06 km; (b) Mm ≥ 1.8, n = 2.42, σ = 0.11, h0 = 0.08 km; (c) Mm ≥ 2.1, n =2.49, σ = 0.16, h0 = 0.08 km (h0 values are above hypocenter determination accuracy 0.03 km).
DISTRIBUTION MODEL FOR THE REGION OF TRIGGERED SHOCKS
Given that the power-law distribution parameter n is practically independent of the magnitude of the triggering event, the radius R of the circle encompassing the expected initiated events with magnitude M ≥ Mm – ΔM is determined by the number of shocks of a given magnitude initiated by the triggering event (trigger productivity).
A triggering event can trigger several dependent shocks constituting a series. As we consider only one hierarchical level, we may suppose that the events in the series are independent of each other. We assume that for each series, the number of the initiated events with magnitudes M ≥ Mm – ΔM obey the Poisson distribution with the mean Λ (Zoller et al., 2013). In this case, the probability that all k initiated shocks occur closer than at distance x from the trigger is Fr(x)k where Fr(x) is distribution described by formula (1). Using the total probability formula, we obtain the distribution of the maximum epicentral distance Rmax from the triggering event to the most distant aftershock in the series:
According to the earthquake productivity law (Shebalin et al., 2020) which was validated for the seismicity of the Khibiny massif (Baranov et al., 2020), the number of the triggered events obeys the exponential distribution with density
Here, the average number of the triggered events is the estimate of parameter L.
For finding the distribution of distances from the triggered shocks to their triggering events over the set of the series, we combine (3) and (4) at x ≥ r0. Thus, we obtain the distribution function
and density
where Fr is the power-law distribution function (1) with density fr (2).
Given that the vertical (along the depth) distances from the triggered shocks to their triggering events also obey the power-law distribution (Fig. 3), the similar relations are also valid for the maximum distances Hmax along the depth.
Formulas (5) and (6) define the model of the distribution of maximum distances where the repeated shocks are expected. The correspondence of this model to the seismicity data for the Khibiny massif is shown in Fig. 4 (the value L ≈ 3 is specified according to (Baranov and Shebalin, 2020); this estimate can also be obtained from Table 1 by calculating the ratio of column N to column Ns values).
Probability density of (a) maximum epicentral distances Rmax, km and (b) vertical (along depth) distances Hmax, km, from triggering events with Mm ≥ 1.5 to their initiated shocks with M ≥ Mm – 1.5. Circles are actual data for 447 series; solid line is approximation by formula (6).
PRACTICAL ASPECTS
In this section, we consider practical aspects of using the averaged model of the distribution of maximum distances. The region where the triggered events with magnitudes M ≥ Mm – ΔM are expected to occur with a given probability can barely be estimated directly from distribution (5) because the power-law decay is only satisfied starting from a certain, albeit small distance from the triggering event, at which about half of all the initiated shocks take place (Table 1). In order to allow for this feature and for the limited spatial extent of the mining activity region, we used the Molchan error diagram (Molchan, 2010) visualizing the dependence of the fraction of the missed target events (the rate of failures-to-predict) ν versus the fraction of space-time alarms τ.
When estimating epicentral distances, we assume the space Ω containing 100% of the triggered events to be a circle with a radius of 2.5 km and a center at the epicenter of the triggering event. This Ω corresponds to the zone controlled by the joint Kirovsk mine. For the Rasvumchorr mine, we assume the same space Ω. We estimate the epicentral alarm zone encompassing the expected triggered events as the circle with the center at the epicenter of the triggering event and with radius Rq calculated for probability q from the inverse function for distribution (5): \({{R}_{q}} = F_{a}^{{ - 1}}\left( q \right)\). (Parameters of distribution (5) are n = 2.28, r0 = 0.134 km (Fig. 2a), L = 3 (Baranov et al., 2020)). We denote this zone by Gq and its area by Sq. Then, the fraction of the alarm space τ is defined by the ratio of Sq to the area SΩ of space Ω, i.e., τ = Sq/SΩ. The rate of missed events ν is the fraction of the triggered events beyond the alarm region Gq.
When estimating distances along the depth (vertical distances), we assume the space Ω in the form of a segment of length HΩ = 1 km centered at the main shock hypocenter, which corresponds to the vertical (along the depth) zone controlled by the mines and contains 100% of the aftershocks. Then, as the alarm zone along the depth accommodating the expected triggered events, we use the vertical segment Vq with the center at the hypocenter of the triggering event and with length Hq calculated for probability q from the inverse function of distribution Fa (5) for depths with parameters n = 2.29 and h0 = 0.06 km (Fig. 3a) and h0 = 3 (Baranov et al., 2020). In this case, the fraction of the alarm space is τ = Hq/HΩ. The fraction ν of the missed target events is the fraction of the repeated shocks that fall beyond the segment Vq.
This shape of the zone corresponds to a cylinder with radius Rq, height Hq, and center at the epicenter of the triggering event. This shape of the zone allows the radius and height of the cylinder to be determined independently, subject to the importance of the forecast.
The dependence of ν on τ for different q is the error trajectory. Diagonal (0; 1) (1; 0) corresponds to a random forecast. The stronger deviation of the error trajectory from the diagonal means the better forecast performance. Parameter q specifies the size of the alarm zone: the larger q means the larger area of Gq or Vq. The error diagram constructed for different q values based on the retrospective forecast of the region of the repeated shocks with M ≥ Mm – 1.5 (Fig. 5) reflects the trade-off between two kinds of errors: the increase in q reduces the probability of a missed event but increases the alarm zone and vice versa. Thus, the scalar parameter q can be characterized as an alarm function (Zechar and Jordan, 2008; Shebalin et al., 2014).
Error diagram for estimating (a) epicentral distance and (b) vertical (along depth) distance from triggering event with Mm ≥ 1.5 to most distant triggered shock with Mm ≥ –1.5; τ is fraction of alarm space; ν is fraction of missed events. Diagonal (0.1)–(10) corresponds to random chance forecast (dashed line). Thick ling is the error trajectory. Circles indicate points corresponding to neutral (0), soft (1), and hard (2) forecast strategies (see text; ν and τ values corresponding to strategies are indicated in Table 2). Thin straight lines show tangent lines to the error trajectory at points 1 and 2 (tangent line to point 2 in panel (b) coincides with abscissa axis).
The q value is chosen subject to the forecast objective. In some cases, it is important that the probability of a second-kind error, i.e., missing an event, is low. The situation when a strong aftershock can cause undesirable consequences is the example. In other cases, it may be necessary to minimize the area where the repeated shocks are expected in order to reduce the cost of continuing the warning status. To formalize the choice of parameter q, we proposed a method of three strategies (Baranov and Shebalin, 2017). The idea of the method is to determine the limiting points on the error trajectory that correspond to the neutral, soft and hard strategies.
The point corresponding to the neutral strategy (point 0 in Fig. 5) is determined from the minimum of the loss function γ = ν + τ which is the sum of the errors of two kinds. This strategy is used when the cost of the two kinds of errors is approximately the same or not known. The point corresponding to the soft strategy (point 1 in Fig. 5) is determined by the position of the tangent line to the error trajectory, at which, because of the trajectory’s closeness to vertical, even a small change in the size of the alarm zone will result, through the decrease in q, in a strongly increased probability of missing an event. Finally, the hard strategy corresponds to the point (2 in Fig. 5) at which the tangent line to the error trajectory is such that the increase in the alarm region will not reduce the fraction of the missed events because of the closeness of the trajectory to horizontal. The q, ν, τ, Rmax, and Hmax values corresponding to the neutral, soft, and hard strategies are presented in Table 2.
Model (5), (6) constructed over the set of the series can be used as a first approximation of the region where the aftershocks triggered by a seismic event with M ≥ 1.5 are expected immediately after its occurrence. The independence of the estimates of the epicentral distance and the estimates along the depth allows us to use different strategies to select the radius and the height of the cylindrical region subject to the location of the main shock.
These estimates for a specific series can be improved by taking into account the first aftershocks. The constructed model in this case can be used as a basic one for testing the models that employ information about the first aftershocks. An example of the use of a basic model for estimating the magnitude of the strongest aftershock and the duration of the hazardous period is presented in (Baranov et al., 2019b; Shebalin and Baranov, 2019).
CONCLUSIONS
Based on the seismicity data for the Khibiny massif, it is shown that the distances between the triggering and triggered events, on average, have a power-law distribution with the exponent that practically does not depend on the magnitude of the triggering event. The established regularity is consistent with the previously obtained conclusions for the aftershocks of the tectonic earthquakes (Huc and Main, 2003; Brodsky, 2006; Richards-Dinger et al., 2010).
This result has an important theoretical value for statistical seismology as it, firstly, validates power-law distribution for weak seismicity with magnitudes 0 ≤ M ≤ 3.3 and, secondly, gives ground to believe that the regularities revealed for tectonic seismicity are also valid at mining in the tectonically loaded rock masses.
In this study, based on earthquake productivity law, we have constructed the model of the maximum distances of the expected aftershocks which allows the estimates to be obtained starting from the time immediately after the main shock. The consistency of the model with the real data is demonstrated. The guidelines for the practical use of this model are substantiated based on the analysis of the error diagram.
REFERENCES
Adushkin, V.V., Blasting-induced seismicity in the European part of Russia, Izv. Phys. Solid Earth, 2013, vol. 49, no. 2, pp. 258–277. https://doi.org/10.7868/S000233371301002X
Adushkin, V.V., Tectonic earthquakes of anthropogenic origin, Izv. Phys. Solid Earth, 2016, vol. 52, no. 2, pp. 173–194. https://doi.org/10.7868/S0002333716020010
Adushkin, V.V., Varypaev, A.V., Kushnir, A.F., and Sa-nina, I.A., Identification of induced seismicity in the fault zone of the Korobkovskoye Deposits (Kursk Magnetic Anomaly) based on observations of a small-aperture seismic array, Dokl. Earth Sci., 2020, vol. 493, no. 1, pp. 548–551. https://doi.org/10.31857/S268673972007004X
Baiesi, M. and Paczuski, M., Scale-free networks of earthquakes and aftershocks, Phys. Rev. E., 2004, vol. 69, no. 6, Paper ID 066106. https://doi.org/10.1103/PhysRevE.69.066106
Baranov, S.V. and Shebalin, P.N., Forecasting aftershock activity: 2. Estimating the area prone to strong aftershocks, Izv. Phys. Solid Earth, 2017, vol. 53, no. 3, pp. 366–384. https://doi.org/10.7868/S0002333717020028
Baranov, S.V. and Shebalin, P.N., Zakonomernosti post-seismicheskikh protsessov i prognoz opasnosti sil’nykh aftershokov (Regularities of Post-Seismic Processes and Strong Aftershock Hazard Prediction), Moscow: RAN, 2019.
Baranov, S.V., Pavlenko, V.A., and Shebalin, P.N., Forecasting aftershock activity: 4. Estimating the maximum magnitude of future aftershocks, Izv. Phys. Solid Earth, 2019a, vol. 55, no. 4, pp. 548–562. https://doi.org/10.31857/S0002-33372019415-32
Baranov, S.V., Zhukova, S.A., Shebalin, P.N., and Motorin, A.Yu., On independence of seismic productivity from environmental disturbance mechanism, Gorn. Inf. Anal. Byull. (Nauchno-Tekh. Zh.), 2019b, no. S37, pp. 333–342. https://doi.org/10.25018/0236-1493-2019-11-37-333-342
Baranov, S.V., Zhukova, S.A., Korchak, P.A., and Shebalin, P.N., Productivity of mining-induced seismicity, Izv. Phys. Solid Earth, 2020, vol. 56, no. 3, pp. 326–336. https://doi.org/10.31857/S0002333720030011
Bayliss, K., Naylor, M., and Main, I.G., Probabilistic identification of earthquake clusters using rescaled nearest neighbor distance networks, Geophys. J. Int., 2019, vol. 217, no. 1, pp. 487–503. https://doi.org/10.1093/gji/ggz034
Clauset, A., Shalizi, C.R., and Newman, M.E.J., Power-law distributions in empirical data, SIAM Review, 2009, vol. 51, no. 4, pp. 661–703. https://doi.org/10.1137/070710111
Dieterich, J.A., Constitutive law for the rate of earthquake production and its application to earthquake clustering, J. Geophys. Res., 1994, vol. 99, no. B2, pp. 2601–2618.
Felzer, K.R. and Brodsky, E.E., Decay of aftershock density with distance indicates triggering by dynamic stress, Nature, 2006, vol. 441, no. 7094, pp. 735–738. https://doi.org/10.1785/0120030069
Hirata, T., Satoh, T., and Ito, K., Fractal structure of spatial distribution of microfracturing in rock, Geophys. J. Int., 1987, vol. 90, no. 2, pp. 369–374. https://doi.org/10.1111/j.1365-246X.1987.tb00732.x
Huc, M. and Main, I.G., Anomalous stress diffusion in earthquake triggering: Correlation length, time dependence, and directionality, J. Geophys. Res.: Solid Earth, 2003, vol. 108, no. B7. https://doi.org/10.1029/2001JB001645
Kagan, Y.Y., Earthquake spatial distribution: the correlation dimension, Geophys. J. Int., 2007, vol. 168, no. 3, pp. 1175–1194. https://doi.org/10.1111/j.1365-246X.2006.03251.x
Kagan, Y.Y. and Knopoff, L., Spatial distribution of earthquakes: the two-point correlation function, Geophys. J. Int., 1980, vol. 62, no. 2, pp. 303–320. https://doi.org/10.1111/j.1365-246X.1980.tb04857.x
Korchak, P.A., Zhukova, S.A., and Men’shikov, P.Yu., Setup and development of seismic monitoring mining region of OAO Apatit, Gorn. Zh., 2014, no. 10, pp. 42–46.
Kozyrev, A.A., Semenova, I.E., Rybin, V.V., Panin, V.I., Fedotova, Yu.V., Konstantinov, K.N., Sal’nikov, I.V., Gadyuchko, A.V., Belousov, V.V., Korchak, P.A., and Streshnev, A.A., Ukazaniya po bezopasnomu vedeniyu gornykh rabot na mestorozhdeniyakh, sklonnykh i opasnykh po gornym udaram (Khibinskie apatit-nefelinovye mestorozhdeniya) (Guidelines for Safe Mining Operations in Rock-Burst Prone and Hazardous Deposits (Khibiny Apatite-Nepheline Deposits)), Apatity: Apatit-Media, 2016.
Kozyrev, A.A., Semenova, I.E., Zhuravleva, O.G., and Panteleev, A.V., Hypothesis of strong seismic event origin in Rasvumchorr Mine on January 9, 2018, Gorn. Inf. Anal. Byull. (Nauchno-Tekh. Zh.), 2018, no. 12, pp. 74–83. https://doi.org/10.25018/0236-1493-2018-12-0-74-83
Kozyrev, A.A., Panin, V.I., Semenova, I.E., and Rybin, V.V., Geomechanical provision of mining operations in the Murmansk Region, Gorn. Zh., 2019, no. 6, pp. 45–50.
Molchan, G., Space-time earthquake prediction: the error diagrams, Pure Appl. Geophys., 2010, vol. 167, nos. 8–9, pp. 907–917. https://doi.org/10.1007/s00024-010-0087-z
Plenkers, K., Kwiatek, G., Nakatani, M., and Dresen, G., Observation of seismic events with frequencies f > 25 kHz at Mponeng deep gold mine, South Africa, Seismol. Res. Lett., 2010, vol. 81, no. 3, pp. 467–479. https://doi.org/10.1785/gssrl.81.3.467
Richards-Dinger, K., Stein, R.S., and Toda, S., Decay of aftershock density with distance does not indicate triggering by dynamic stress, Nature, 2010, vol. 467, no. 7315, pp. 583–586. https://doi.org/10.1038/nature09402
Scholz, C.H., Earthquakes and friction laws, Nature, 1998, vol. 391, no. 6662, pp. 37–42. https://doi.org/10.1038/34097
Shebalin, P.N. and Baranov, S.V., Forecasting aftershock activity: 5. Estimating the duration of a hazardous period, Izv. Phys. Solid Earth, 2019, vol. 55, no. 5, pp. 719–732. https://doi.org/10.31857/S0002-33372019522-37
Shebalin, P., Narteau, C., Holschneider, M., and Zechar, J., Combining earthquake forecast models using differential probability gains, Earth, Planets Space, 2014, vol. 66, artic. 37, pp. 1–14.
Shebalin, P.N., Narteau, C., and Baranov, S.V., Earthquake productivity law, Geophys. J. Int., 2020, vol. 222, pp. 1264–1269. https://doi.org/10.1093/gji/ggaa252
Smirnov, V.B. and Ponomarev, A.V., Fizika perekhodnykh rezhimov seismichnosti (Physics of Transient Seismicity), Moscow: RAN, 2020.
Smirnov, V.B., Ponomarev, A.V., Stanchits, S.A., Potanina, M.G., Patonin, A.V., Dresen, G., Narteau, C., Bernard, P., and Stroganova, S.M., Laboratory modeling of aftershock sequences: stress dependences of the Omori and Gutenberg–Richter parameters, Izv. Phys. Solid Earth, 2019, vol. 55, no. 1, pp. 124–137. https://doi.org/10.31857/S0002-333720191149-165
Smirnov, V.B., Kartseva, T.I., Ponomarev, A.V., Patonin, A.V., Bernard, P., Mikhailov, V.O., and Potanina, M.G., On the Relationship between the Omori and Gutenberg–Richter parameters in aftershock sequences, Izv. Phys. Solid Earth, 2020, vol. 56, no. 5, pp. 605–622. https://doi.org/10.31857/S0002333720050117
Woodward, K. and Wesseloo, J., Observed spatial and temporal behaviour of seismic rock mass response to blasting, J. South. Afr. Inst. Min. Metall., 2015, vol. 115, pp. 1045–1056. https://doi.org/10.1007/s00024-017-1570-6
Zaliapin, I. and Ben-Zion, Y., A global classification and characterization of earthquake clusters, Geophys. J. Int., 2016, vol. 207, no. 1, pp. 608–634. https://doi.org/10.1093/gji/ggw300
Zoller, G., Holschneider, M., and Hainzl, S., The maximum earthquake magnitude in a time horizon: Theory and case studies, Bull. Seismol. Soc. Am., 2013, vol. 103, no. 2A, pp. 860–875. https://doi.org/10.1785/0120120013
ACKNOWLEDGMENTS
We are grateful to the reviewers for their deep and meaningful analysis of the work and for their valuable comments.
Funding
The work includes the results obtained in the project no. 19-05-00812 supported by the Russian Foundation for Basic Research and the results obtained in partial fulfillment of state contract from the Ministry of Science and Higher Education of Russian Federation (under project no. 075-01304-20).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Translated by M. Nazarenko
Rights and permissions
Open Access. This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Baranov, S.V., Motorin, A.Y. & Shebalin, P.N. Spatial Distribution of Triggered Earthquakes in the Conditions of Mining-Induced Seismicity. Izv., Phys. Solid Earth 57, 520–528 (2021). https://doi.org/10.1134/S1069351321040029
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1069351321040029