Seismic Noise H/V Spectral Ratio Can Be Inverted Jointly with Receiver Functions

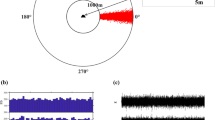
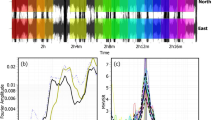
The possibility of jointly inverting the receiver function waveforms and the seismic noise horizontal-to-vertical spectral ratio to study the Earth’s structure is substantiated. Both data types are widely used for constructing a velocity model beneath a single seismic station. The main difference between the methods is associated with the different frequency content of input data which is 0.02–0.2 Hz in receiver functions and 0.5–20 Hz in seismic noise. It is shown that notwithstanding these differences, the joint inversion approach more effectively reconstructs the model of the medium in case when a station is underlain by a complexly structured sedimentary cover. In the practical implementation, the parameters of both seismic methods are described in a flat-layer representation of the medium. Besides, both methods are most sensitive to the depth distribution of S-wave velocities. In this work, we use records from the Monakovo seismic station, Nizhny Novgorod region, Russia, to construct a model of the medium consistent with both data types. It is shown that the allowance for the H/V spectral curve in the receiver function interpretation provides additional constraints on the small-scale structure of the upper part of the velocity section thus stabilizing the reconstruction procedure.

APPENDIX

EFFECT OF LOW-VELOCITY NEAR-SURFACE LAYER ON THE RECEIVER FUNCTION WAVEFORM

To assess the effect of the near-surface low-velocity layer on the receiver function waveform, we carried out numerical modeling. As a basic velocity model in the depth interval from 0 to 700 km, we used the IASP91 standard model (Kennett and Engdahl, 1991). In this interval, the model has four seismic interfaces at the depths of 20, 35, 410 and 660 km between which the velocity increases with a weak gradient down the section. The initial model was approximated by a stack of 1-km thick layers down to a depth of 700 km. The rest of the model was described by an elastic half-space with the IASP91 parameters for this depth. Layers’ densities were calculated by the Birch’s formula (Birch, 1961). This approximation allows calculation of synthetic seismograms by one of the simple and effective matrix methods. In particular, we used the Thomson–Haskell propagator method (Haskell, 1953).

The input signal was a plane P-wave in the form of a Gaussian pulse with unit amplitude incident from below from the half-space to the bottom of the stack of the layers. The length of the input signal was 1.6 s. The ray parameter is 6.3 s/deg. Using the calculated free-surface displacement components, we calculated the receiver functions. Calculations were carried out for four models. The calculated synthetic receiver functions are shown in Fig. 4.

Fig. 4.

Synthetic receiver functions calculated for IASP91 model with added low-velocity near-surface layers of varying thickness. Layers’ thicknesses in meters are indicated at beginning of corresponding traces.

The first trace from the bottom corresponds to the initial standard IASP91 model. The primary and multiple converted phases are marked here by arrows. The numbers in the indices indicate the formation depth of the primary converted wave. For convenient and transparent identification of phases, this trace is left unchanged. The results of the subsequent calculations were low-pass Butterworth filtered with a corner period of 5 s. It is these periods that are typical for real measurements.

In the subsequent experiments, the upper part of the standard model was replaced by one or more layers with typical elastic parameters of certain sedimentary rocks (Table A1).

Table A1.   Elastic parameter of layers used in numerical simulation

We have analyzed three models. The first model contained a water-saturated layer with a thickness of 200 m and the second model contained a 500 m thick clay layer. In the third model, we changed the standard model within the upper 1600 m. Three types of layers were considered. The first layer of water saturated rock has a thickness of 100 m. The 500 m thick second layer is composed of clay. The third, base layer is limestone with a thickness of 1000 m. This structure of sediments and these values of elastic parameters are typical for the central part of the East European platform (Dortman, 1984).

The results of the calculations are shown in Fig. 4. It can be seen that the thin sedimentary layer does not impede the identification of the primary and multiple converted waves formed both in the crust and at the mantle interfaces. The thicker and more consolidated clay layer distorts the record drastically. This layer produces reverberations lasting longer than 60 s after the arrival of the original P-wave which obscure observation of crustal conversions and prevent reliable identification of the converted wave from the 410 km interface. At the same time, as follows from the last seismogram, the complication of the structure of sediments does not fundamentally change the waveforms compared to a simple single-layer model.

This is illustrated in Fig. 5 which shows the receiver functions obtained by processing the records from the stations located in three regions with a sedimentary layer of different thickness. Here, NOR denotes the central station of the NORSAR array, Norway, southwestern Baltic Shield. The sedimentary layer beneath this station is fairly thin (a few tens of meters) and it virtually does not mask the Moho conversions. The thickness of the sedimentary layer beneath the OBN seismic station (Obninsk, Kaluga region, Russia, East European platform) is about 1500 m. Therefore, the respective seismogram is highly contaminated by noise despite the fact that the station is installed in a mine at a depth of 30 m in a limestone layer. The receiver function calculated from the records by the KAL station (Calcutta, India, Hindustan platform) is shown in Fig. 5 as an absolute “champion” in the amplitude of the converted wave arising at the contact of the sediment and bedrock (Kosarev et al., 2013). The amplitude of this converted phase is at least four times the amplitude of the Moho conversion on the Baltic Shield.

Fig. 5.

Observed receiver functions for three stations installed in regions with different thickness of sedimentary cover. Station names are indicated at beginning of corresponding seismogram.