Modeling of a Crisis in the Biophysical Process by the Method of Predicative Hybrid Structures

Abstract

Crisis processes of biosystems often develop according to scenarios of rapid collapse, which cannot be predicted by statistical methods. This paper develops a method for constructing hybrid computational models using event-hierarchy representation for biophysical processes. System events calculated by the algorithm change the order of calculation of equations according to a given set of rules. The rules of physically conditioned redefinition of the right-hand sides of differential equations are used. The predicates employ the calculations of a group of accompanying characteristics, which are an integral part of the controlled biophysical dynamics. The model is investigated by presenting a computational scenario with a set of parameters, initial values, and an algorithm for making decisions about changing the impact for discrete time. Using computational experiments, a real outcome scenario for a situation that leads to the collapse of a biophysical system at a controlled level of exposure is described. The scenario sets the logic for making control decisions to change the level of external pressure on the natural environment. It is shown as a result of modeling that the transition of the process to an oscillatory mode leads to the choice of a risky control mode. It has been established that the dynamics of many real water populations has a point of threshold reduction in the efficiency of replenishment of stocks. The model scenario uses transformations of the phase portrait of iterations, which, in the presence of disconnected boundaries of the areas of attraction of alternative attractors and a strange chaotic repeller, lead to the uncertainty effects arising due to chaotic modes in a deterministic model. The properties of the described model scenario with a chaotic regime of dynamics are confirmed by the example of the catch of oceanic species of crustaceans.

1 INTRODUCTION

Due to unforeseen perturbations, the problems of regulating biophysical processes become even more difficult, and so the development of computational methods for analyzing the nonlinearity of situations with a description of the logic of the impact is relevant. Evolutionarily settled modes of functioning of trophic chains, which include regular cycles of populations, are destroyed without maintaining species diversity. Excessive exploitation of economically valuable populations violates the regulatory mechanisms that maintain the balance of the ratio of species in the community, which leads to the expansion of the ranges of species that are useless for fishing and the occupation of the ecological niche by harmful invaders. Aquatic ecosystems turn out to be unbalanced. Features for the problems of control of a competitive biophysical environment are created not only by a rapidly changing volatile environment, but also by the adaptive nature of the reproduction process in communities with strong concurrence.

For the optimal control of biosystems, various mathematical approaches were proposed, which are based on the principles of physical modeling of events by analogy with models of phase transitions. For living systems, methods taking the random effects of the environment into account [1], as well as dynamic programming and the theory of monotone operators [2], were used. Most authors assumed the main task to lie in improving the rules for the distribution of quotas [3]. The problem is complicated by the factors of migration and variability of the spatial distribution of populations [4]. As has been noted by many authors [5], intense fishing, due to selectivity both in terms of the timing of the catch and in terms of the size of individuals, affects the biophysical properties and genetic diversity of the individuals that make up the population. The selective action to eliminate fast-growing individuals changes the average parameters of growth and fertility. These are the characteristics responsible for the success of the reproductive cycle.

Elaborating a universal model for choosing the optimal (from the point of view of profit) and reliable strategy for long-term fishing will be an insoluble problem for a long time. Errors during optimization entail the phenomenon of structural collapse, which must be determined in a timely manner by characteristic features. Optimization according to the theory of maximum sustainable yield, which is implemented over an indefinite period of time in the practice of its application carries a risk both for populations and for the economy of regions [6]. The collapse of supplies means a long cessation of fishing and depression of the economy [7]. Regulated fishing leads to unexpected degradation of bioresources quite often [8]. The difficulty lies in the fact that the key signs of dynamics in crisis situations are diverse [9]. The object of control in this case is a complex biophysical system with nonlinear threshold effects in the regulation of its internal physical and chemical processes.

The purpose of the work is to develop a scenario approach to the study of nonlinear phenomena for controlled biophysical systems based on the discrete component of the trajectory of the model obtained using tunable differential equations. A computational model was developed with the inclusion of the variability of generational survival factors according to the principles of ontogenetic development stages, which are event-dependent on the growth rate of individuals in the population. The novelty of the model construction method is in the formalization of different types of events with respect to time. The novelty of the model analysis with influence is in the comparative evaluation of computational scenarios when choosing one of the valid control logic options. The key idea of the analysis is the assessment of a given situation with options for its occurrence with different algorithms for changing the impact.

The algorithmically formalized logic of changing the impact, together with a set of parameters and certain initial conditions of the equations, will constitute an original interpretation of the model situation under consideration. The practical part of the work includes a scenario analysis based on catch statistics for a special situation that ended with a rapid commercial degradation of the population of the Paralithodes camtschaticus crab in the Gulf of Alaska.

2 1. FORMALIZATION OF HIERARCHICAL CONTINUOUS TIME WITH EVENTS

The technique of organizing rearrangements in the calculation of equations is required for modeling many specific problems [9]. To adapt the scenario methods to the real process, it is necessary to represent the model time as a sequence of tuples to determine the sequence of these reswitches. Points in time for events that lead to rearrangements in a system of continuous equations can be defined in different ways—explicitly or indirectly—since biological problems are specific and biosystem processes develop variably. Currently, “hybrid models” is a broad and interdisciplinary term [11]. A more precise and narrower definition needs to be given. For our purposes, the term “a predictive computational structure with an event type of time” is more accurate. Various authors have used the term “hybrid systems” to refer to many structures that are different and have dissimilar properties for numerical calculations. In the context of dynamically redefined systems, we can talk about discontinuous nonlinearities or glued calculations. The form of visualization of such a continuous-discrete structure is the formalism of hybrid automata, as extensions of directed graphs. Graph vertices correspond to state-change modes, and edges correspond to transitions between alternative state-change modes (but not between states themselves) specified by the conditions of Boolean functions. A specific hybrid automaton can be a nested element for a higher-order aggregated automaton in the process hierarchy of a heterogeneous system [12].

For practical problems of ecology, it is necessary to introduce additional conditions into the models for the start and end of the action of factors, since the course of processes can change abruptly due to a small perturbation of the conditions: the rate of decomposition of organic matter in eutrophic lakes changes dramatically with an increase in temperature [13]. More often, abrupt changes are not expressed by a shift in the values of a set of indicators in a tabular function, but affect the form of nonlinearity in their regulation. Completely continuous models of the age structure of populations [14] are not suitable for commercial species of fish and crabs, for which fluctuations in juvenile mortality are significant. For the trophic chain in continuous models, cascades of period doubling bifurcations arise [15], but complicating the behavior is not our task.

The composing of continuous segments or time frames can be algorithmically implemented in various formats, and there is no universal method for building a model with dynamic rebuilds. In biological models, discontinuity is required to describe both structural and qualitative changes. One can choose redefinitions that are strictly required, algorithmically predefined on the timeline, or optional. It is allowable to take advantage of the random consequences of other processes, as in the presentation of an antigen in the first phase of the immune response. Reconstructing and choosing an alternative equation in our model will become necessary with a special ratio of the calculated values: we will evaluate these points in the state space as special points.

For such tasks, several different time formats with a continuous and discrete component are used. For this problem, we will choose an interpretation that is convenient for modeling the logic of the process and studying the model situation of fishing in a series of comparative computational experiments with a predicatively changed form of influence. Let us set a life cycle of standard length T. In an aquatic organism (fish or crustaceans), it is accompanied by metamorphoses. Let us compose a partition of the life cycle of the view with framing the hierarchy of continuous time intervals. Inside large frames, we leave place for numbered events tⁱ. We formalize hybrid and “event” time for computational experiments as a multiset of ordered elements—tuples:

$$\bigcup\limits_n {\left\{ {\partial {{L}_{n}},{{{\left\{ {\bigcup\limits_i {[{{t}_{0}},{{t}^{i}},{{t}^{{i + 1}}},T]} } \right\}}}_{n}},\partial {{R}_{n}}} \right\}} ,$$

where i is the event number in the frame segment before T and n is the current frame number in generational order. The formalism of time with two discrete components leaves faces ∂L and ∂R both to the right and to the left of frame number n. Faces ∂L and ∂R between time frames, but not included in the frame in the form of interruptions, were needed to perform rearrangements in the system transitions selected according to the conditions and start calculating the dynamics of the next adjacent generation and setting the magnitude of the impact. The task of structuring the model time is to accurately enter the elements of eventfulness into the control algorithm by the impact, since t¹, t², and tⁱ will be set from the calculations of other entirely continuous additional variables. The float-length time between calculated events should be formatted into fixed frames, rather than simply to introduce eventness without explicit framing.

The essence of manipulations with time is that such a controlled model of the population process is formed on the basis of a dynamically redefined system of equations. Factors of population reduction change sharply between the stages of ontogenetic development, which is due to biochemical processes during the endogenous feeding of individuals [16]. The second idea is to establish events from the state of a set of predicates, which will be followed by the changes in the calculations of the state of the biophysical system. It is then convenient to vary the control action by the scenario logic of the computational experiment.

3 2. CONTINUOUS TIME FRAMING AND SEQUENCE OF EVENTS

For a modeling method that takes into account biological discontinuity, we propose a computational structure that changes according to logical rules with three successive redefinable forms of the right side. The value of population number N(t) in each frame changes from N(0) = λS to R = N(T). S is the traditional designation for an adult spawning stock. Variable R conveniently reflects the replenishment of the biophysical system. The model is formalized by a differential equation with a set of possible forms for the right side supplemented by a set of predicates for changing the calculation mode—functions with a set of values {0; 1}. The predicate is given by a mathematical ratio of continuously changing arguments (obeys the rules of Boolean algebra). By default, predicates for t₀ should be equal to zero, P(x, y) = 0, but for tⁱ they take the value P(x, y) = 1 from the state of their arguments; otherwise, a loop error occurs. Arguments of Boolean functions are variables from auxiliary calculation equations related to the dynamics of N(t).

The sequence of time intervals before the reproductive age of each of the n generations is set by combining time frames with a tuple for the calculated events:

$$t \in [0,T] \equiv \bigcup\limits_i {\{ [{{t}_{0}},{{t}^{i}},{{t}^{{i + 1}}},T]\} ,\quad i = 1...3} .$$

Numbered events tⁱ in frames are ontogenetic “interruptions.” Let us compare them with three consecutive forms for the right side. Let us write the equations for the reduction in the number of generations from N(0) with three stages of ontogenetic development up to moment T:

$$\frac{{dN}}{{dt}} = \left\{ \begin{gathered} - ({{\alpha }_{1}}w(t)N(t) + \beta )N(t),\quad {{P}_{1}}(t) \\ - {{\alpha }_{2}}N(t){\text{/}}w(\tau ) - \beta N(t),\quad {{P}_{2}}(t,w(t) \\ - {{\alpha }_{3}}w(t)N(t - \chi ) - \beta ,\quad {{P}_{3}}(t,w(t)). \\ \end{gathered} \right.)$$

(1)

Here, coefficients α₁ < α₂ < α₃ are the interpretable parameters for juvenile mortality depending on the size of the generation itself and β is the density-independent loss parameter. One of the equations includes the delay t–χ to account for the depletion of food resources.

Three predicates P₁, P₂, and P₃ are set the moments of stopping the calculations of each of the three forms of the right side, which will create conditions for the completion of activity for the form of the right side of the equation:

$$\begin{gathered} {{P}_{1}}(\neg t < \tau ),\quad {{P}_{2}}(t \geqslant \tau ,t \ne T,\neg {{w}_{t}} < {{w}_{k}}), \\ {{P}_{3}}(t = T,{{w}_{t}} > {{w}_{k}}). \\ \end{gathered} $$

(1.1)

In (1.1), a transitional level of development w_k to exit a generation from a quadratically determined mortality rate is used. We wrote two predicates with logical negation: $\neg t < \tau$, $\neg {{w}_{t}} < {{w}_{k}}$. Events are possible if these relationships are violated. Calculation (1) occurs with the while{1} loop algorithm until P = 1. Predicates (1.1) must always uniquely define transitions, and so their redundancy is permitted. To avoid ambiguity, one can use additional logical variables that change state when the transition already occurred, but cannot be chosen again by the hybrid automaton algorithm.

Compiling continuous-event time as a multiset of elements $\langle {{t}_{0}},{{t}^{i}},{{t}^{i}}{{^{ + }}^{1}}\rangle$ means that the tool environment algorithm considers a sequence of frames for the life-cycle time of a separate nth generation.

Let, by definition, a frame be the standard lifetime for a generation. There are intraframe events within each frame with onset t₀, which we denoted by index tⁱ. For each form of the right side at the time of the event, the initial conditions associated with the previous calculations are calculated. Since the rearrangements of the right side of (1) occur predicatively, the current values P₁, P₂, and P₃ are an important element of the model. Let us classify transitions: forms I, only by accounting for timing t, and forms II caused by internal ratios of the calculated indicators. In the type II transition, the change of the right side of (1) occurs after comparing the ratios of the values of the internal model variables. The inequalities in (1.1) are related to the calculation of an auxiliary indicator for w(t).

The strategy of using different accompanying characteristics will allow expanding the model. This is necessary, since population processes are variable and nonequilibrium even without the influence of catching. The fertility of aquatic organisms is associated with both body mass and the growth rate of individuals [17]. Let us find in the model the relationship between the growth rate of juveniles and their mortality [18]. Main structure (1) for N(t) should be solved numerically in conjunction with an auxiliary indicator—size-development index w(t) of individuals of the generation:

$$\frac{{dw}}{{dt}} = \frac{\sigma }{{\sqrt[3]{{{{{(N(t) + \delta )}}^{2}}}}}},$$

(2)

where δ is the correction factor and σ is fixed and reflects the abundance of food resources.

We use calculations with R = N(T) = φ(N(0)) for numerical analysis of iterations R_n+1 = φ(R_n). To calculate the dynamics of the new (n + 1)th generation, the initial conditions for the first equation in structure (1) are reinitialized:

$$\begin{gathered} N{{(0)}_{{n + 1}}} = \lambda {{S}_{n}}, \\ {{S}_{n}} = \left( {N{{{(T)}}_{n}} + \sum\limits_{m = 1}^k {{{\upsilon }_{m}}N{{{(T)}}_{{n - m}}}} } \right), \\ \end{gathered} $$

where υ_m is the postspawn survival index for a series of previous m generations and S is the population of stock ready for reproduction with average fertility λ. A model in the Rand Model Designer environment can be adapted for multiple generations living together. The mathematical basis for the analysis of the discrete part of the model trajectory will be the theory of the occurrence of bifurcations in nonunimodal iterations with nonconstant Schwarzian. The biological substantiation of the method is based on a well-developed theory of population-replenishment development [19]. According to the theory, several qualitatively different types of dependence between the stock and the efficiency of its reproduction are admissible. It is known from experiments that the growth rate of surviving older individuals can sharply increase with an increase in the density of juvenile fish [20].

4 3. RIGID AND SOFT QUALITATIVE TRANSFORMATIONS IN THE DYNAMICS OF ITERATIONS

Having obtained functional dependence N(0) → N(T) ≡ φ(N(0)) after numerical solution of equations with N(0) = λS in (1), (1.1) along with (2) for biologically allowable values N(0), S ∈, one can estimate iteration dynamics properties $\varphi (...\varphi ({{x}_{0}}))$ of this dependence. S is the stock population ready for reproduction with average fertility λ. Not all changes in regulation are threshold. It is biologically unreliable to change the basic population characteristics abruptly. A simple change in the parameters during rearrangements in (1) will not solve our problems, and an increase in the number of parameters seems problematic.

With a small population, the effect of random unfavorable factors in the reproduction of populations is large [21]. We developed a method for taking into account the variability of factors in the form of a point injection into a predicatively redefined dynamic system (1) of trigger functions—smoothly varying coefficients Ψ(n) ≠ const for iterations ${{\varphi }^{n}}({{x}_{n}}_{{ - 1}},\Psi (n))$ with a limited range of their values. Trigger functions are constant over the entire length of the frame of continuous model time $[{{t}_{0}},{{t}^{i}},{{t}^{{i + 1}}},T]$ and change the value when changing the frame number: n: = n + 1. The method is applicable in different models. When approaching some region of the system state, the value of Ψ will increase rapidly, but smoothly. We use this method because the use of rebuilding with predicates from the generation state P(N(T)) is not convincing. We do not use the population number for unnecessary changes in the structure of equations, since two event rearrangements are sufficient for the description.

For the equation of the reduction of the number of generations in (1), mortality rates are specially separated: quadratic αN² and linear βN. The value of w(t) for parameter α takes into account the fast depletion of resources needed for a development as the total biomass increases. We take into account the reproduction loss at stage t₀. The effect can be sharply manifested precisely for low density $S \to \min \varphi$ of adults [22]. The effect of reproductive activity loss is implemented in the model by a dynamic coefficient along with βN. Its effect depends on value of the parent population S, from which we calculated initial conditions N(0). The level of the impact of Ψ has to be limited. The range of values E(Ψ) on the right has a finite limit, and then our soft switch Ψ does not interfere with the calculations. This will allow us to implement a smooth shutdown of the negative factor:

$$\begin{gathered} \Psi (S) = 1 + \exp ( - \zeta {{S}^{2}}), \\ {\mathop{\lim }_{{S \to \infty }}}\Psi (S) = 1,\quad \Psi (0) = 2, \\ \frac{{dN}}{{dt}} = - \alpha w(t){{N}^{2}}(t) - \Psi [S]\,\beta N(t), \\ \end{gathered} $$

(3)

where parameter ζ < 1 reflects the threshold-effect significance level. Using this method, we took into account smooth changes in regulation, while in the hybrid system we described hard and threshold changes in the dynamics of the decrease in the number of juveniles. Threshold effects manifest themselves not only in controlled population dynamics, but also affect many biological processes, such as the development of an immune response and the development and treatment of cancer [23].

5 4. SITUATION OF A TYPICAL COLLAPSE OF THE COMMERCIAL POPULATION OF AQUATIC ORGANISMS

Several extreme variants of development for population dynamics are known. Some of these processes are associated with crises, such as the bottleneck effect, and others with rapid population explosions. System control in the mode of abrupt eruptive changes is an unrealizable task. Often a crisis can be foreseen, but the degradation of bioresources does not always occur gradually, but often in the form of a collapse.

The main assertion that we want to emphasize in the article is that a sharp collapse is fundamentally different from the systematic and monotonous depletion of reserves from the point of view of the theory of dynamical systems. The disappearance of commercial stocks of the Atlantic cod Gadus morhua off the coast of North America created a devastating effect with economic consequences due to the instant cessation of fishing and without recovery [24]. Since 1992, special expert commissions and monitoring organizations have discussed the situation with cod degradation. Errors in the regulation of fisheries, unreliability of stock estimates, error in methods and selectivity of harvesting, and accompanying natural factors—warming ocean currents—were noted. Ichthyological commissions have not reached a consensus on the reasons for the collapse; moreover, they are not clear why there was no quick recovery after the moratorium. Contradictions in expert assessments always arise when there are several materially interested groups among experts, which is also a hidden problem of the expert control method. For the case of cod collapse, we proposed a model [25], in which the situation developed after the loss of unstable equilibrium, and the main unaccounted-for factor was increased cannibalism of cod with an abundance of its own juveniles. Unstable equilibria x* for iterations arise after a tangent bifurcation. Since, in this case, the stability criterion $\left| {\varphi '(x{\text{*}})} \right|$ differs slightly from the bifurcation $\left| {\varphi '(x{\text{*}})} \right|$ = 1; then, the trajectory can stay in their vicinity for quite a long time. In some cases, x* can retain stability even at critical condition $\left| {\varphi '(x{\text{*}})} \right| = 1$. The model can be improved for other cases of degradation by changing the topology of the boundaries of the attraction regions of attractors.

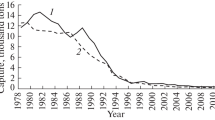
Previously, there were several situations of collapse of the fishery of large predators with different dynamics, but not all collapse events have attracted general attention. Many failures can be attributed to randomnicity. The cod crisis off the coast of Labrador was long regarded as unique in commercial ichthyology. We will give another not very well-known example that is interesting from the point of view of the problem of managing adaptive biosystems for modeling the dynamics of degradation of valuable stores. Figure 1 shows data on the collapse of the king crab stock near the Aleutian Peninsula and neighboring islands in the Pacific Ocean in 1985. In this case, fishing was also carried out that was regulated by quotas and selective in terms of the size of the individuals taken [26]. The crab harvest peaked in 1966. In the scenario, the time to collapse was much longer than in the case of cod off the coast of Labrador, where the time interval from peak to eventual collapse and complete moratorium on fishing took 14 years. The economic losses in the two situations are comparable, and a temporary precautionary moratorium was logical in both cases, but no such decision was made. Experts often do not make the necessary decisions in time when such decisions would entail recognizing that their previously chosen strategy was incorrect. A typical example is the much-criticized delay in declaring a COVID-19 pandemic in 2020 by the World Health Organization.

Fig. 1.

Dynamics of collapse of crab stock off the coast of Alaska in 1985 from [26].

The graph shows two sharp drops in the dynamics of crab catches in million pounds. This is due to a decrease in stock S. Between the crises, 18 years of active removal of individuals passed. In the scenario model, instead of the mass, it is expedient to calculate the number of individuals Y_n withdrawn from stock S during the fishing season. The situation of crab collapse is theoretically more interesting, since a strong oscillatory mode of stock abundance between the first and final crisis of the fishery is obvious. For cod, pseudostabilization was observed. The scenario of the depletion of the king crab population differs from the dynamics of the cod crisis precisely by oscillating phenomena. It was difficult for statisticians to foresee a rapid collapse and understand its causes. The cod Gadus morhua and the crab Paralithodes camtschaticus are long-lived large predators. It was believed that such species could not collapse. Collapse is common in species such as anchovies, but Peruvian anchovies always recover.

6 5. ANALYSIS OF THE PROPERTIES OF A NONLINEAR COMPUTATIONAL MODEL

The obtained numerical solution of the model with the calculated N(T) we use in the form of functional iterations: R_n+1 = φ(R_n) – q_nR_n , where q ∈ [0,1) is set as a fraction of commercial withdrawal. When managing the fishery, the value of q is set by experts for each year n. Initial fertility λ of the species is an important parameter for scenarios.

In the phase plane of iterations, we obtain the separation of the set of available starting points R₀ of trajectories by one repeller point. So, iterations will obtain two areas of attraction for two “competing” attractors. Dependence φ will have more than one maximum, but, for us, the position of first maximum R_max from the origin, as well as local minimum R_min, is important (R_min > R_max) with the meaningful property $\varphi ({{R}_{{{\text{max}}}}}) > {{R}_{{{\text{min}}}}}$. Thus, two conditions of Singer’s theorem [27] for a nonunimodal function, which are necessary to implement the scenario of transition to a global chaotic attractor through a cascade of bifurcations of cycle period doubling, are not satisfied. With a smooth change in parameter λ of such a model, two alternative cycles of an even period will arise, p = 2. As we noted, the Feigenbaum scenario is not relevant in this problem. It is known that doubling bifurcations p = 2^{i + 1} arise in different iterative models of populations. Chaotization of the trajectory through the bifurcation cascade can be obtained in iterations for the Ricoeur model, ${{x}_{{n + 1}}} = a{{x}_{n}}{{e}^{{ - b{{x}_{n}}}}},\,\,a > {{e}^{2}}$, and in the Shepard model, ${{x}_{{n + 1}}} = a{{x}_{n}}{\text{/}}1 + {{\left( {{{x}_{n}}{\text{/}}{{S}_{{\max }}}} \right)}^{z}}$, z > 2. The bifurcation parameters of these models have opposite meanings: the reproductive potential a and environmental-resistance factor z. The addition of q, x_{n + 1} = $a{{x}_{n}}{{e}^{{ - b{{x}_{n}}}}}$ – qx_n for a = e² + ε induces an opposite bifurcation p = 2^{i – 1}. This is a consequence of the generality of the mechanism of formation of the Cantor attractor in the renormalization theory and has no biological interpretation. Fractal asymptotic subsets of iterations in biology are often difficult to interpret.

The set of descriptive means of the dynamics of iterations is wide, but limited. For iterations R_{n + 1} = φ(R_n), three topological forms of attractors are available: a finite period cycle or equilibrium point x* = φ(x*), an attractor similar to the Cantor set, and an interval attractor, in the form of a conjugation of an infinite set of segments. For iterations taking into account the changing external perturbation x_n = f(x_{n – 1}) ± Θ(n), there are three types of bifurcations—rearrangements, type, and number of attractors—which can be direct or inverse. Attractors other than cycles can instantly lose their invariance property f(Λ)  ∈ Λ, which depends on the position of their attraction region $\Omega$ near the boundary $\partial \Omega$. The attractor can be separated into parts or intersect with the  boundary $\partial \Omega \notin \Omega$ of its area of attraction $\Omega :\forall {{x}_{0}} \in \Omega ,{{\lim }_{{n \to \infty }}}{{\varphi }^{n}}({{x}_{0}}) = \Lambda$.

7 6. SCENARIO WITH REFLEXIVE CONTROL UNDER THE FINAL COLLAPSE

Let us analyze the properties of the collapse scenario in an experiment with the logic of managing commercial withdrawals q_n. We will formulate the logic of changing control action q for the scenario in the following rules corresponding to criteria adopted in the 1980s:

$$\begin{gathered} \sum\limits_{n = 1}^5 {{{q}_{n}}} {{R}_{n}} \leqslant 0.5\sum\limits_{n = 1}^5 {{{R}_{n}}} ,\quad q = {\text{const}}{\text{,}} \\ \sum\limits_{n = 1}^5 {{{q}_{n}}} {{R}_{n}} > 0.5\sum\limits_{n = 1}^5 {{{R}_{n}}} ,\quad {{q}_{{n + 1}}} = 1.2q, \\ 0.2\sum\limits_{n = 1}^5 {{{q}_{n}}} {{R}_{n}} > 0.8{{q}_{{n + 1}}}{{R}_{{n + 1}}},\quad {{q}_{{n + 2}}} = 0.8{{q}_{{n + 1}}}, \\ 0.2\sum\limits_{n = 1}^5 {{{q}_{n}}} {{R}_{n}} > 0.5{{q}_{{n + 1}}}{{R}_{{n + 1}}},\quad {{q}_{{n + 2}}} = 0.6{{q}_{{n + 1}}}, \\ 0.2\sum\limits_{n = 1}^5 {{{q}_{n}}} {{R}_{n}} > 0.1{{q}_{{n + 1}}}{{R}_{{n + 1}}},\quad {{q}_{{n + 2}}} = 0. \\ \end{gathered} $$

For the mathematical implementation of such a degradation scenario of two stages (as in Fig. 1) , we propose a scenario with two metamorphoses in the dynamics of iterations. For this purpose, it is necessary to obtain the dependence when solving three glued Cauchy problems with four nontrivial stationary states $\varphi (R_{i}^{*}) = R_{i}^{*}$ with the condition $R_{1}^{*} < R_{2}^{*} < R_{3}^{*} < R_{4}^{*}$.

We implement the first metamorphosis by smoothly increasing the share of removal q, which will cause a reverse tangent bifurcation for $R_{4}^{*}$ merging of stable and unstable equilibrium, causing the loss of the most attractional equilibrium state. For the necessary reconstruction of the phase portrait, it is necessary to have three unstable stationary points while maintaining the stability of the zero equilibrium. The event-redefinable system of Eqs. (1) and (2) scales the final dependence along the S axis in computational scenarios. It is relevant to purposefully change the positions of extrema φ(R), as shown in Fig. 2 (curves of the model dependence relative to the bisector of the coordinate angle), due to external conditions. Trigger-function $\Psi$ does not change the relative position for of fourth stable equilibrium $R_{4}^{*}$, but acts on position minφ(R) relative to precritical unstable repeller $R_{2}^{*}.$ An important property for the projections of the extremum points of the local maximum and minimum is the inequality φ(R_max) > R_min : φ, which displays the maximum always to the right of the minimum.

Fig. 2.

Transformation of extrema and nontrivial equilibria in functional dependence φ(λS): (a) in the case minφ(R) < $R_{2}^{*}$, maxφ(R) > $R_{3}^{*}$; (b) in the case minφ(R) > $R_{2}^{*}$, maxφ(R) > $R_{4}^{*}$ > $R_{3}^{*}$.

The second metamorphosis of the phase portrait of our iterations is the boundary crisis of the interval attractor, which remains after the merging of stable and unstable equilibria. The effect occurs upon contact with the boundary of its own area of attraction. Let there be a neighborhood of a local maximum where the value of φ slightly exceeds the value of φ at the point of the third repeller: φ(maxφ(N(0)) ± $\varepsilon ) > R_{3}^{*}.$ Here, the initial position of trajectory point R₀ < $R_{3}^{*}$ corresponds to the subset from the interval:

$${{R}_{0}} \in (R_{1}^{*},R_{3}^{*}) \cap \{ {{\varphi }^{{ - n}}}(R_{2}^{*})\} .$$

In the implementation of this scenario, through a short regime that is indistinguishable from stochastic fluctuations, the model crab population will reach a level of high stable abundance in a finite number of steps: ${{\varphi }^{\vartheta }}({{R}_{0}}) = R_{4}^{*},\vartheta < \infty .$ We denote by $\{ {{\varphi }^{{ - n}}}(R_{2}^{*})\}$ the total set of preimage points of second repeller $R_{2}^{*}$. The specified points as preimages are excluded from the area of attraction of attractors, and they are never attracted to attractors. If direct preimages are accessible for $R_{2}^{*}$ both to the right and to the left of the point, this will make the interval attraction domain $R_{4}^{*}$–${{\Omega }_{2}}$ disconnected. In the model, repeller $R_{2}^{*}$ exists in all scenarios and always has preimages on both the right and left. Points $R_{3}^{*},R_{4}^{*}$ may disappear after the reverse tangent bifurcation. Similarly, point $R_{1}^{*}$ for φ exists in all scenarios, but the preimage for the first repeller depends on the action of soft trigger Ψ.

Let us compose a set of parameters for a computational experiment for a situation in which the commercial crab population, after an unstable existence, has recovered to a stable equilibrium and is optimal for its food supply. The basis for the evaluation will be a model season of 12 model months. Crab catches Y = R_nq_n without forcing fishing capacity are increasing. After a spontaneous increase in the volume of catch to the historical record Y → max, experts make a justified decision to raise the annual quota, ${{\bar {q}}_{n}} = 0.62$. It is quite logical that the catches of crab for the first four seasons after the increase in withdrawals show historically record values for the fishery. After three successful seasons, catches drop sharply.

The volumes of commercial stocks of crab bypass the local minimum of the reproduction curve φ, avoiding falling into the ε-vicinity of critical state $R_{1}^{*}$.

According to the current statistical methodology, the forecasts of experts have taken into account the high efficiency of crab reproduction in the previous 5 years. It appears to statisticians that, after the first fall, the catches start to return to their former volumes. For experts, there is no reason to adjust the management of the fishery in order to reduce share q of withdrawals.

The duration of growth in catch volume Y after the minimum is associated with volatility effects. After an increase in the fishing intensity, the value of stock S_n breaks into an aperiodic mode, but in a limited range of values. Experts can see fluctuations not around the rest point, but more like regular stochastic fluctuations caused by the instability of environmental conditions. The decision to minimize the share of withdrawals to q = 0.12 is rejected after intense fluctuations. With q = 0.3 set, after passing the minimum in the scenario, we observe an irretrievable drop in catches, as in the computational experiment in Fig. 3.

Fig. 3.

A computational scenario of catch dynamics in a stock-collapse situation.

Aperiodic fluctuations end just as abruptly as they arise after the first drop in catches. The second drop in cod and crab catches was labeled as a “collapse,” while the previous drop in catches received little attention, but the first drop in catches is larger in percentage terms. During the first crisis, catches dropped sharply by four times, but this did not lead to a seasonal moratorium on fishing. As a precaution in such a situation, the logical solution is to introduce a seasonal moratorium and conduct a study to accurately account for the biomass of the spawning stock. The fishery continued with unstable fluctuations in crab stocks with unchanged fishing effort and a moderately favorable forecast. According to the principles of nonlinear dynamics, such behavior is regarded as a sign of the presence of critical points, but statistical methods cannot establish breakdown points for the stock, where the relationship between stock and replenishment resembles a step function.

Modeling showed that the path to the final crisis consists of two transitional regimes. In the computational experiment, the scenario of the collapse of the red king crab commercial stocks in 1985 developed from two phases, and their duration depended on the increase in ${{\bar {q}}_{n}}$ with intensification of the catch. If a timely moratorium is not introduced, the second phase of degradation occurs after nine model seasons in the format of the model time of the computing environment with the transition through the critical unstable equilibrium threshold. After the degradation phase $R_{1}^{*} > \min \varphi (\lambda S)$, the reproduction of the crab population does not compensate the natural loss of already-spawning generations. To restore the population, the introduction of adult crabs is necessary.

Many models of local interaction of populations have been proposed, but the problem of describing a number of specific extreme cases (outbreaks, crises, pulsating series of peaks with attenuation, etc.) remains relevant. For controlled populations, the model must include an algorithm for changing the impact and explain the situation from the point of view of experts. Scenario models are now actively used to test different fisheries regulation rules and assess the risk of violation of biological management guidelines [28]. The question is to what extent scenarios based on cohort models can account for nonlinear effects.

Collapses of Atlantic cod and red king crab are provoked by the notion of a prosperous state of bioresources and, most importantly, by an overestimation of the effectiveness of replenishing these reserves. Before the critical threshold, the reproduction efficiency is quite high according to our model. This property of imaginary recovery leads experts to have incorrect expectations. A similar situation is well known in the financial and investment markets, which goes by the name of “dead cat bounces.” This is a scenario of price behavior in financial markets, which indicates a false upward trend in prices after a sharp crisis in a financial asset. A collapse in the value of the asset is then inevitable.

The development of situations in the model up to the point of collapse confirms that the ideas of optimal organization and most profitable strategy for the exploitation of bioresources in the case of quota distribution are dangerous. The originality of our collapse modeling lies in that the phenomenon in the scenario develops according to the internal logic of expert fishery management, which cannot take into account threshold effects and evaluate modes of unstable fluctuations.

The optimal state of the stock for fishing is close to the critical threshold. For a fishery to collapse, a small error in the estimates of the allocated quota is sufficient. We believe that a rational tactic for regulation is to limit the infrastructural possibilities of fishing (characteristics of ships, cell sizes, and area of the mouth of trawls). It is important to keep the fishing effort at a level acceptable for the biosystem (fished space of the water basin per unit of time), but not to limit the volume of production Y by quotas. Modern powerful trawlers and their fishing gear have become too effective, and so now it is tactically possible to limit their catch rates—to leave the prey with some chance of salvation.

8 7. FEATURES OF THE PHASE PORTRAIT OF A HYBRID DYNAMICAL SYSTEM

The occurrence of irregular fluctuations is a consequence of the shape of the curve φ with extrema. The instability of intermediate results at different positions of initial point ${{R}_{0}}$ of the trajectory is associated with riddled region I in the phase space. The segment includes a scattered continuum set of subintervals from two attraction regions  Ω₁ and Ω₂ of two attractors Λ₁ and Λ₂, but the boundaries of all subintervals do not belong to these attraction regions and form an invariant set—a strange repeller. There are a number of chaotic regimes in the dynamics of iterations that are not associated with closed attracting sets, these being the phenomena of “horseshoe dynamics” or the effect of “chaotic scattering” [29].

The position of the boundary of interval I determines the mapping of points R_min > R_max. Such an interval I = [φ(R_min), φ(R_max)] is placed between two extrema of the two model dependence. Since the very existence of $R_{3}^{*}$ depends on q, the fixed interval $[R_{1}^{*},R_{3}^{*}]$ itself is not important. The range of values on the segment is called “riddled,” because the initial points R₀ ∈ [φ(R_min), φ(R_max)], which are attracted to the attractor, are everywhere adjacent to the points not attracted to $R_{4}^{*}$. The association of the sets of those points, which, under the action of iterations, are mapped to unstable repeller equilibrium positions, are excluded from interval I. If the unstable stationary points on the graph of replenishment efficiency φ have more than one direct preimage, then, after the first iteration, point $R_{2}^{{ - 1*}}$ will be mapped to repeller $\varphi (R_{2}^{{ - 1*\text{r}}}) = R_{2}^{*}.$ As a result of all the above conditions being met, an aperiodic regime arises. Here, ${{\varphi }^{{ - 1}}}(R_{2}^{*}) = R_{2}^{{ - 1*\text{r}}}$ means the inverse iteration of function φ into the right inverse image of point $R_{2}^{*}$.

At the moment when a tangent bifurcation occurs, unstable and stable points $R_{3}^{*},R_{4}^{*}$ merge into one critical point $R_{C}^{*},\varphi '(R_{C}^{*}) = 1,$ which disappears. This is how the first fall of the crab catch is described. Interval I between the mappings of the extrema of function φ will include interval attractor Λ ⊂ [φ(R_min), φ(R_max)]. within itself. In the order in which types of attractors are listed in Gookenheimer’s theorem [30], this is the third topological type of ω-limiting sets of iterations indicated there out of three possible types of attractors. Closed interval I contains attractor Λ ⊂ I of interval type. Λ denotes a closed invariant subset of I, but the subset Λ is not connected, since any ε-neighborhood of the point $\forall {{R}_{0}} \in \Lambda$ contains nonattracting points from the invariant and continuous set ϒ, which minimally consists of all preimages of $R_{2}^{*},$ that has both right and left direct preimages: $\{ {{\varphi }^{{ - n}}}(R_{2}^{{ - 1*\text{r}}})$, ${{\varphi }^{{ - n}}}(R_{2}^{{ - 1*l}})\} .$ The dimension of the “strange repeller” will be the entire association of points R₀ scattered in I without attraction:

$$\Upsilon = \bigcup\limits_n^\infty {{{\varphi }^{{ - n}}}(R_{2}^{*})} ,{{\varphi }^{{ - n}}}(R_{1}^{*}),{{\varphi }^{{ - n}}}(R_{3}^{*}).$$

The discrete component of the trajectory $\{ {{\varphi }^{n}}({{R}_{0}})\}$ obtained in this scenario from the starting point given by the condition ${{R}_{0}} \notin \{ {{\varphi }^{{ - n}}}(R_{2}^{*})\}$, has the ability to fall into the ε-neighborhood of chaotic repeller $\Upsilon$, which consists of the set of all nonattracting points and arising when changing the position of the extrema of dependence φ(R). Next, for $\exists {{R}_{0}},{{R}_{0}} \in I,{{R}_{0}} \notin \Upsilon$, and $\varphi ({{R}_{0}}) <$ $R_{1}^{*}$, already the intervals in Λ will not be a closed and invariant subset, where the condition φ(Λ) ∈ Λ is met. In I , we observe chaotic motion in the finite number of iterations ${{\varphi }^{k}},0 < k < \infty$ with one option to end the chaotic mode ${{\lim }_{{n \to d}}}{{\varphi }^{n}}({{R}_{0}}) = 0,$ k < d < ∞.

After the first drop in numbers for the population, these rearrangements mean a sharp transition to a state of strong irregular fluctuations with pronounced peaks, but this is a reversible state. The population may recover if a management decision is made immediately and the catch is significantly reduced to 0.4q.

In addition to the position of the repellers, the duration of irregular oscillations under intense fishing pressure depends on the position of the curve $\varphi$ at its minimum. When there is a shift of value φ(R) in the extremum R_min down along the ordinate axis and $\varphi ({{R}_{{\min }}}) < R_{1}^{*}$, then a boundary crisis is realized for attractor Λ, composed of a multitude of intervals, and points $\exists {{x}_{0}} \in \Lambda ,\,\,{{\lim }_{{n \to \infty }}}{{\varphi }^{n}}({{x}_{0}}) = 0$ appear. Point $R_{1}^{*}$ corresponds to unstable equilibrium for a population at critical abundance. When the inequality R₀ < $R_{1}^{*} - \varepsilon$ is met, then the irreversible degradation of the stock is realized in a finite number of iterations ${{\varphi }^{k}}({{R}_{0}}) = 0$. The collapse scenario is reflected in the form R₀ ∉ ϒ, φ^k(R₀) = 0, k < ∞. The duration of observation of aperiodic fluctuations is not constant due to the sensitivity to disturbances R₀ ± ε near the point that we choose as the initial one in the computational experiment, but this reproduces the natural uncertainty for a given fishery object.

9 CONCLUSIONS

In studies of nonlinear functional iterations, three nonlinear phenomena that are known called “crises” [31]. In addition to the “basin-boundary crisis,” an internal crisis and a “merging crisis” specific to the period doubling scenario p = 2ⁱ, i → ∞, are identified for the cycles. Crises are not caused by transformations of the topological types of attractors, but are associated with rearrangements of the position of the attractor and its adjacent unstable invariant sets. Under the boundary crisis effect, attractor Λ, in our case consisting of a continuum of disordered and disconnected intervals, comes into contact with the left side of domain Ω.

Fish-stock collapses are not only due to poorly regulated fisheries. The collapse of the whitefish of Lake Ontario occurred after an invasion of the sea-lamprey parasite. Salinization was an important factor in the Azov and Caspian seas. Freshwater species drastically reduced their range with a reduction in the freshwater runoff of the Don and Volga [32]. In the Caspian Sea, cyclic transgressions and regressions of the sea level occur, which entails the transformation of the faunal complex [33]. As the situation with Caspian sturgeons showed, the release of juveniles is not a very effective method of recovery. The degradation of the four previously numerous Caspian sturgeon populations before their inclusion in the Red Book did not occur in the form of a collapse: from 1979 to 2010, the fishery depleted stocks for a long time and systematically [34]. The situation of the depletion of the bioresources of the Caspian Sea is not directly related to the problems of expert management of exploitation—experts well understood the outcome of the process [35], and the degradation of their stock was predicted by many quite a long time ago.