Optimization of Measurement of the Interaction Force Vector in Atomic Force Microscopy

Abstract

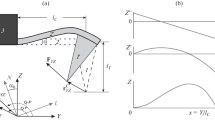
The optimization of measurements of three spatial components of the probe–sample interaction force and the corresponding “ideal cantilever” displacement vector is considered. To determine these components using an atomic force microscope with the optical beam deflection scheme, it is necessary to measure the bending angles at least at two points on the rectangular cantilever, as well as the torsion angle at any of these points. It is proved analytically that one of the optimal points is the intersection of the probe axis with the cantilever plane. A technique for calculating the optimal position of the other point is developed. An experiment concerning mapping of the force and displacement vector is performed, and satisfactory agreement with the theory is achieved.

3. ANALYTICAL APPENDIX

3.1. Formulation of the Problem

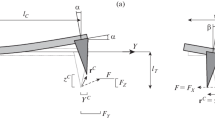
Let us write the general expression for bending angle profile α(x) of the cantilever console under the action of force F_YZ = (F_Y, F_Z) applied to the probe tip, lying in plane YZ, and causing the displacement of the tip of the undeformed “ideal cantilever” probe in this plane along vector ${\mathbf{r}}_{{YZ}}^{C}$ = (Y^C, Z^C):

$$\begin{gathered} y = \alpha (x) = \frac{{6(\lambda {{F}_{Y}} + {{F}_{Z}})x - 3{{F}_{Z}}{{x}^{2}}}}{{2{{k}_{C}}{{l}_{C}}}} \\ = \frac{{(6\lambda {{Z}^{C}} - 2{{Y}^{C}})x - (6\lambda {{Z}^{C}} - 3{{Y}^{C}}){{x}^{2}}}}{{{{l}_{T}}}} = ax - b{{x}^{2}}. \\ \end{gathered} $$

(A.1)

We have used the following parameters: ratio λ = l_T/l_C of probe height l_T to console length l_C; flexural stiffness coefficient k_C of the console, and normalized coordinate x = Y/l_C of the laser focus in the OBD scheme on the console, x ∈ [0; 1].

Coefficients a and b in expression (A.1) are determined unambiguously from the measured values of y₁ and y₂ at two different points x₁ and x₂ of the console:

$$\left\{ \begin{gathered} {{y}_{1}}\, = \,a{{x}_{1}} - bx_{1}^{2} \hfill \\ {{y}_{2}}\, = \,a{{x}_{2}} - bx_{2}^{2} \hfill \\ \end{gathered} \right. \to \left\{ \begin{gathered} a\, = \,\frac{1}{{({{x}_{2}} - {{x}_{1}})}}\left( {{{x}_{2}}\frac{{{{y}_{1}}}}{{{{x}_{1}}}} - {{x}_{1}}\frac{{{{y}_{2}}}}{{{{x}_{2}}}}} \right), \hfill \\ b\, = \,\frac{1}{{({{x}_{2}} - {{x}_{1}})}}\left( {\frac{{{{y}_{1}}}}{{{{x}_{1}}}} - \frac{{{{y}_{2}}}}{{{{x}_{2}}}}} \right). \hfill \\ \end{gathered} \right.$$

(A.2)

Let us assume that errors of measurements obey on the following relations on average:

$$\begin{gathered} \langle {{(\Delta {{x}_{1}})}^{2}}\rangle \, = \,\langle {{(\Delta {{x}_{2}})}^{2}}\rangle \, = \,\sigma _{x}^{2},\quad \langle {{(\Delta {{y}_{1}})}^{2}}\rangle \, = \,\langle {{(\Delta {{y}_{2}})}^{2}}\rangle \, = \,\sigma _{y}^{2}, \\ \langle \Delta {{x}_{1}}\Delta {{x}_{2}}\rangle = \langle \Delta {{y}_{1}}\Delta {{y}_{2}}\rangle = \langle \Delta {{y}_{1}}\Delta {{x}_{1}}\rangle = \langle \Delta {{y}_{1}}\Delta {{x}_{2}}\rangle \\ = \langle \Delta {{x}_{1}}\Delta {{y}_{2}}\rangle = \langle \Delta {{x}_{2}}\Delta {{y}_{2}}\rangle = 0. \\ \end{gathered} $$

(A.3)

Let us formulate the problem. For given standard deviations $\sigma _{x}^{2}$ and $\sigma _{y}^{2}$, find the values of x₁, x₂ ∈ [0; 1], ensuring minimal standard deviations $\sigma _{a}^{2}$ and $\sigma _{b}^{2}$:

$$\left\{ \begin{gathered} \sigma _{a}^{2}\, = \,\left[ {{{{\left( {\frac{{\partial a}}{{\partial {{x}_{1}}}}} \right)}}^{2}}\, + \,{{{\left( {\frac{{\partial a}}{{\partial {{x}_{2}}}}} \right)}}^{2}}} \right]\sigma _{x}^{2}\, + \,\left[ {{{{\left( {\frac{{\partial a}}{{\partial {{y}_{1}}}}} \right)}}^{2}}\, + \,{{{\left( {\frac{{\partial a}}{{\partial {{y}_{2}}}}} \right)}}^{2}}} \right]\sigma _{y}^{2}, \hfill \\ \sigma _{b}^{2}\, = \,\left[ {{{{\left( {\frac{{\partial b}}{{\partial {{x}_{1}}}}} \right)}}^{2}}\, + \,{{{\left( {\frac{{\partial b}}{{\partial {{x}_{2}}}}} \right)}}^{2}}} \right]\sigma _{x}^{2}\, + \,\left[ {{{{\left( {\frac{{\partial b}}{{\partial {{y}_{1}}}}} \right)}}^{2}}\, + \,{{{\left( {\frac{{\partial b}}{{\partial {{y}_{2}}}}} \right)}}^{2}}} \right]\sigma _{y}^{2}. \hfill \\ \end{gathered} \right.$$

(A.4)

For generality, we will minimize the linear combination of the standard deviations

$$M = {{\cos }^{2}}\theta \sigma _{a}^{2} + {{\sin }^{2}}\theta \sigma _{b}^{2} = m_{x}^{2}\sigma _{x}^{2} + m_{y}^{2}\sigma _{y}^{2}.$$

(A.5)

Expressions for $m_{x}^{2}$ and $m_{y}^{2}$ follow from formulas (A.4). Parameter θ is conditional and auxiliary. Depending on the choice of its value, the following errors are significant: only $\sigma _{a}^{2}$, cosθ = 1; only $\sigma _{b}^{2}$, sinθ = 1; and both errors, cosθ = sinθ.

3.2. Case σ_x ≪ σ_y

Let us consider $m_{y}^{2}$, i.e., the square of the sensitivity to the error in y:

$$m_{y}^{2}\sigma _{y}^{2} = {{\cos }^{2}}\theta \sigma _{a}^{2} + {{\sin }^{2}}\theta \sigma _{b}^{2}.$$

(A.6a)

Taking relations (A.2) and (A.4) into account,

$${{(\partial a{\text{/}}\partial {{y}_{1}})}^{2}} + {{(\partial a{\text{/}}\partial {{y}_{2}})}^{2}} = (x_{1}^{4} + x_{2}^{4}){\text{/}}(x_{1}^{2}x_{2}^{2}{{({{x}_{2}} - {{x}_{1}})}^{2}})$$

and

$${{(\partial b{\text{/}}\partial {{y}_{1}})}^{2}} + {{(\partial b{\text{/}}\partial {{y}_{2}})}^{2}} = (x_{1}^{2} + x_{2}^{2}){\text{/}}(x_{1}^{2}x_{2}^{2}{{({{x}_{2}} - {{x}_{1}})}^{2}})$$

we obtain

$$m_{y}^{2} = \frac{{{{{\cos }}^{2}}\theta (x_{1}^{4} + x_{2}^{4}) + {{{\sin }}^{2}}\theta (x_{1}^{2} + x_{2}^{2})}}{{x_{1}^{2}x_{2}^{2}{{{({{x}_{2}} - {{x}_{1}})}}^{2}}}}.$$

(A.6b)

To test for an extremum, we introduce new variables 2d = x₂ – x₁ and p² = x₁x₂ and write expression (A.6b) in the form

$$m_{y}^{2}\, = \,{\text{co}}{{{\text{s}}}^{2}}\theta \left( {\frac{{4{{d}^{2}}}}{{{{p}^{4}}}}\, + \,\frac{4}{{{{p}^{2}}}}\, + \,\frac{1}{{2{{d}^{2}}}}} \right)\, + \,{\text{si}}{{{\text{n}}}^{2}}\theta \left( {\frac{1}{{{{p}^{4}}}}\, + \,\frac{1}{{{{p}^{2}}{{d}^{2}}}}} \right).$$

(A.6c)

If d ≠ 0, we have ∂($m_{y}^{2}$)/∂p < 0. Consequently, for any fixed d, the value of $m_{y}^{2}$ decreases with increasing p. Therefore, for each x₂ ∈ [2d, 1], the minimum $m_{y}^{2}$ is achieved for maximal possible p² = (x₂ – 2d)x₂, i.e., at point x₂ = x_2(extr) = 1. Taking these considerations into account, relation (A.6b) can be written as a function of one variable x₁ = x:

$$m_{y}^{2} = \frac{{1 + {{x}^{2}}{{{\sin }}^{2}}\theta + {{x}^{4}}{{{\cos }}^{2}}\theta }}{{{{x}^{2}}{{{(1 - x)}}^{2}}}}.$$

(A.6d)

Let us find one more coordinate of the extremum:

$$\frac{{\partial (m_{y}^{2})}}{{\partial x}} = 0 \to {{x}^{4}}{{\cos }^{2}}\theta + {{x}^{3}}{{\sin }^{2}}\theta + 2x - 1 = 0.$$

(A.7)

The root of this equation weakly depends on θ: x_1(extr) ∈ [0.453; 0.475], x_1(extr) ≅ 0.464.

Thus, if only the error of measurements of the console bending angle is significant, the most accurate determination of the applied force vector is ensured by measurements at points x_2(extr) = 1 and x_1(extr) ≅ 0.464.

3.3. Case σ_y ≪ σ_x

Let us consider $m_{x}^{2}$, i.e., the square of the sensitivity to the error in x:

$$m_{x}^{2}\sigma _{x}^{2} = {{\cos }^{2}}\theta m_{{ax}}^{2}\sigma _{x}^{2} + {{\sin }^{2}}\theta m_{{bx}}^{2}\sigma _{x}^{2}$$

(A.8a)

Using relations (A.2), (A.4), and (A.8a) and taking into account the relations

$$m_{{ax}}^{2} = {{\left( {\frac{{\partial a}}{{\partial {{x}_{1}}}}} \right)}^{2}} + {{\left( {\frac{{\partial a}}{{\partial {{x}_{2}}}}} \right)}^{2}} = \frac{{x_{1}^{4}{{{(2b{{x}_{2}} - a)}}^{2}} + x_{2}^{4}{{{(2b{{x}_{1}} - a)}}^{2}}}}{{x_{1}^{2}x_{2}^{2}{{{({{x}_{2}} - {{x}_{1}})}}^{2}}}},$$

(A.8b)

$$m_{{bx}}^{2} = {{\left( {\frac{{\partial b}}{{\partial {{x}_{1}}}}} \right)}^{2}} + {{\left( {\frac{{\partial b}}{{\partial {{x}_{2}}}}} \right)}^{2}} = \frac{{x_{1}^{2}{{{(2b{{x}_{2}} - a)}}^{2}} + x_{2}^{2}{{{(2b{{x}_{1}} - a)}}^{2}}}}{{x_{1}^{2}x_{2}^{2}{{{({{x}_{2}} - {{x}_{1}})}}^{2}}}},$$

(A.8c)

we obtain

$$m_{x}^{2} = \frac{{({{{\cos }}^{2}}\theta x_{1}^{4} + {{{\sin }}^{2}}\theta x_{1}^{2}){{{(2b{{x}_{2}} - a)}}^{2}} + ({{{\cos }}^{2}}\theta x_{2}^{4} + {{{\sin }}^{2}}\theta x_{2}^{2}){{{(2b{{x}_{1}} - a)}}^{2}}}}{{x_{1}^{2}x_{2}^{2}{{{({{x}_{2}} - {{x}_{1}})}}^{2}}}}.$$

(A.8d)

Let us introduce new variables u and ${v}$:

$$\left\{ \begin{gathered} {{x}_{1}} = \frac{a}{{2b}}\frac{1}{u} = {v}{{x}_{2}}, \hfill \\ {{x}_{2}} = \frac{a}{{2b}}\frac{1}{{u{v}}}. \hfill \\ \end{gathered} \right.$$

(A.9)

Assuming that 0 ≤ x₁ ≤ x₂ ≤ 1, we obtain 0 ≤ ${v}$ ≤ 1 and u ≥ a/(2b${v}$). Substituting relation (A.9) into (A.8d), we obtain, taking (A.8a) into account,

$$\begin{gathered} m_{{ax}}^{2} = 4{{b}^{2}}\left[ {\frac{{1 + {{{v}}^{2}}}}{{{{{(1 - {v})}}^{2}}}}{{{(u - {{u}_{1}})}}^{2}} + \frac{{{{{v}}^{2}}}}{{1 + {{{v}}^{4}}}}} \right], \\ {{u}_{1}} = \frac{{1 + {{{v}}^{3}}}}{{1 + {{{v}}^{4}}}}, \\ \end{gathered} $$

(A.10)

$$\begin{gathered} m_{{bx}}^{2} = \frac{{16{{b}^{2}}}}{{{{a}^{2}}}}\left[ {\frac{{{{{v}}^{2}}(1 + {{{v}}^{2}})}}{{{{{(1 - {v})}}^{2}}}}{{{(u - {{u}_{2}})}}^{2}}{{u}^{2}} + \frac{{{{{v}}^{2}}}}{{1 + {{{v}}^{4}}}}{{u}^{2}}} \right], \\ {{u}_{2}} = \frac{{1 + {v}}}{{1 + {{{v}}^{2}}}}. \\ \end{gathered} $$

(A.11)

Using these relations and inequality 0 ≤ ${v}$ ≤ 1, we also obtain

$${{u}_{2}}({v}) - {{u}_{1}}({v}) = \frac{{(1 - {v})(1 - {{{v}}^{2}}){v}}}{{(1 + {{{v}}^{2}})(1 + {{{v}}^{4}})}} \geqslant 0.$$

(A.12)

It can be seen that ∂($m_{{ax}}^{2}$)/∂u ≥ 0 and ∂($m_{{bx}}^{2}$)/∂u ≥ 0 as long as u ≥ u₂(${v}$) ≥ u₁(${v}$). Indeed, the square brackets in relation (A.10) contain the expression for a parabola increasing for u ≥ u₁(${v}$). The square brackets in relation (A.11) enclose a more cumbersome expression. However, since its left term increases for u for u ≥ u₂(${v}$), while the right term increases in all cases, their sum always increases for u ≥ u₂(${v}$).

Consequently, if

$${{u}_{2}}({v}) \geqslant \frac{a}{{2b}}\frac{1}{{v}},$$

(A.13)

$${\text{which is equivalent to}}\quad \frac{{{v} + {{{v}}^{2}}}}{{1 + {{{v}}^{2}}}} \leqslant \frac{a}{{2b}},$$

$m_{{ax}}^{2}$ and $m_{{bx}}^{2}$ are minimal on curve u = a/(2b${v}$); i.e., x₂ = x_2(extr) = 1 (see relation (A.9)). Since ${v}$ ∈ [0; 1], relation (A.13) always holds when a ≥ 2b > 0.

Let us now suppose that 0 < a < 2b and consider first the case when $m_{x}^{2}$ = $m_{{ax}}^{2}$ (θ = 0).

For each ${v}$ = const from region II in Fig. 4 such that ${{{v}}_{1}}$ ≤ ${v}$ ≤ 1, expression (A.10) is minimal at point u = u₁(${v}$) on the curve. On this curve, $m_{{ax}}^{2}$ = 4b²${{{v}}^{2}}$//(1 + ${{{v}}^{4}}$) depends only on ${v}$ and is minimal at the point of intersection with the hyperbola u = a/(2b${v}$). The value of ${v}$ = ${{{v}}_{1}}$ is determined as the root of equation u₁(${v}$) = a/(2b${v}$), or

$$\frac{{{v} + {{{v}}^{4}}}}{{1 + {{{v}}^{4}}}} = \frac{a}{{2b}}.$$

(A.14)

Fig. 4.

Search for the minimum of $m_{{ax}}^{2}$ (A.9). Hyperbola u  = a/(2b${v}$); black solid curve corresponding to x₂ = 1 bounds domains I and II from below of admissible values of u. For each ${v}$ = const, vertical dotted arrows indicate the direction of variations of variable u, which reduce $m_{{ax}}^{2}$. In domain I, 0 ≤ ${v}$ < ${{{v}}_{1}}$, $m_{{ax}}^{2}$ attains its maximum on the hyperbola. For each ${v}$= const in domain II, ${{{v}}_{1}}$ ≤ ${v}$ ≤ 1, the value of $m_{{ax}}^{2}$ is the smallest at the corresponding point on solid curve u = u₁(${v}$). In turn, the value of $m_{{ax}}^{2}$ along this curve decreases with a decrease in ${v}$ (dashed arrow under this curve) and attains its minimum at point ${v}$ = ${{{v}}_{1}}$ of intersection with the hyperbola.

In region I in Fig. 4, 0 ≤ ${v}$ ≤ ${{{v}}_{1}}$, the minimum $m_{{ax}}^{2}$ for each ${v}$ = const is achieved immediately on the hyperbola.

Consequently, for all admissible values of u and ${v}$, the value of $m_{{ax}}^{2}$ is minimal on this hyperbola (see also the caption to Fig. 4 and relations (A.9)), i.e., at the boundary corresponding to x₂ = x_2(extr) = 1.

Thus, if $m_{x}^{2}$ = $m_{{ax}}^{2}$, the minimum of the square of the sensitivity in x lies in region x₁ ≤ ${{{v}}_{1}}$, x₂ = 1. Substituting x₁ = ${v}$ and x₂ = 1 into relation (A.10), we find that the other coordinate x₁ = x_1(extr) of the minimum of $m_{{ax}}^{2}$ can be determined from the minimization of the following expression in ${v}$:

$$m_{{ax}}^{2} = \frac{1}{{{{{v}}^{2}}{{{(1 - {v})}}^{2}}}}[{{{v}}^{4}}{{(2b - a)}^{2}} + {{(2b{v} - a)}^{2}}].$$

(A.15)

Alternatively, differentiating this expression, from the root of equation

$$\begin{gathered} {{P}_{a}}({v}) = {{(2b - a)}^{2}}{{{v}}^{4}} + 4{{b}^{2}}{{{v}}^{3}} - 6ab{{{v}}^{2}} \\ \, + (2ab + 2{{a}^{2}}){v} - {{a}^{2}} = 0 \\ \end{gathered} $$

(A.16)

we obtain

$$\begin{gathered} {{P}_{a}}(0) = - {{a}^{2}} < 0, \\ {{P}_{a}}(a{\text{/}}2b) = {{(a(2b - a){\text{/}}2b)}^{2}} > 0 \\ \end{gathered} $$

and

$${{P}_{a}}(1) = 2{{(2b - a)}^{2}} > 0,$$

and the roots always exist. These roots depend on a/b, and we must choose the minimal root, which for 0 < a < 2b is smaller than ${{{v}}_{1}}$ defined by Eq. (A.14). It should also be noted that x₁ ≤ ${{{v}}_{1}}$ < a/2b if a/2b < 1.

Let us pass to the case when $m_{x}^{2}$ = $m_{{bx}}^{2}$ (θ = π/2).

We write expressions (A.11) in a different form:

$$\begin{gathered} m_{{bx}}^{2} = \frac{{16{{b}^{2}}}}{{{{a}^{2}}}}[c{{(u - {{u}_{2}})}^{2}}{{u}^{2}} + d{{u}^{2}}], \\ {{u}_{2}} = \frac{{1 + {v}}}{{1 + {{{v}}^{2}}}},\quad c = \frac{{{{{v}}^{2}}(1 + {{{v}}^{2}})}}{{{{{(1 - {v})}}^{2}}}},\quad d = \frac{{{{{v}}^{2}}}}{{1 + {{{v}}^{4}}}}. \\ \end{gathered} $$

(A.17)

Differentiating these relations with respect to u, we obtain the following condition for the extrema of $m_{{bx}}^{2}$:

$$(2c{{u}^{2}} - 3c{{u}_{2}}u + cu_{2}^{2} + d)u = 0.$$

(A.18)

Three roots of this equation can be evaluated easily:

$$\begin{gathered} u = 0,\quad {{u}_{ \pm }} = \frac{{3{{u}_{2}}}}{4} \pm \sqrt {{{{\left( {\frac{{{{u}_{2}}}}{4}} \right)}}^{2}} - \frac{d}{{2c}}} \\ = \frac{{3(1 + {v}) \pm \sqrt {{{{(1 + {v})}}^{2}} - 8{{{(1 - {v})}}^{2}}} }}{{4(1 + {{{v}}^{2}})}}. \\ \end{gathered} $$

(A.19)

Figure 5 illustrates the search for the points at which the minimum of $m_{{bx}}^{2}$ is attained. In two particular cases in Fig. 5, $m_{{bx}}^{2}$ is minimal in domain I on hyperbolas u = 0.16/${v}$ and, accordingly, u = 0.62/${v}$. For each ${v}$ = const in domain II in both figures, $m_{{bx}}^{2}$ is minimal on curve u = u₊.

Fig. 5.

Search for the minimum of $m_{{bx}}^{2}$ in two particular cases. (a) Hyperbola bounding from below the domain of admissible values of u and not intersecting curves u₊(${v}$) and u_–(${v}$). (b) Hyperbola intersects curve u₊(${v}$) (see also the explanation in the caption to Fig. 4).

Let us prove that the following inequality holds on curve u = u₊:

$$\frac{{d(m_{{bx}}^{2})}}{{d{v}}} > 0.$$

(A.20)

If this is true, the values of $m_{{bx}}^{2}$ on this curve are the smallest: at branching point ${{{v}}_{2}}$, where u_– = u₊ (Fig. 5a), and at point ${{{v}}_{3}}$ of the interaction with the curve u = u₊ = 0.62/${v}$ (Fig. 5b). In the former case, $m_{{bx}}^{2}$ continues to decrease during the downward motion along the arrow from the branching point to the point of intersection of vertical line ${v}$ = ${{{v}}_{2}}$ with curve u = 0.16/${v}$, where the minimum of $m_{{bx}}^{2}$ is reached and condition x₂  = 1 holds. In the latter case, the minimum is attained immediately at the intersection with the hyperbola, which automatically corresponds to the condition x₂ = 1.

In accordance with Eq. (A.18), d($m_{{bx}}^{2}$)/d$u{{{\text{|}}}_{{u = {{u}_{ + }}}}}$ = 0. Consequently, we have

$$\begin{gathered} {{\left. {\frac{{d(m_{{bx}}^{2})}}{{d{v}}}} \right|}_{{u = {{u}_{ + }}}}} = \frac{{\partial (m_{{bx}}^{2})}}{{\partial {v}}} + \frac{{\partial (m_{{bx}}^{2})}}{{\partial u}}\frac{{d{{u}_{ + }}}}{{d{v}}} = \frac{{\partial (m_{{bx}}^{2})}}{{\partial {v}}} \\ = u_{ + }^{2}\left[ {\frac{{\partial c}}{{\partial {v}}}{{{({{u}_{2}} - {{u}_{ + }})}}^{2}} + 2c({{u}_{2}} - {{u}_{ + }})\frac{{\partial {{u}_{2}}}}{{\partial {v}}} + \frac{{\partial d}}{{\partial {v}}}} \right]. \\ \end{gathered} $$

(A.21)

For relations (A.19), we obtain

$$\begin{gathered} {{u}_{2}} - {{u}_{ + }} = {{u}_{2}}{\text{/}}4 - \sqrt {{{{({{u}_{2}}{\text{/}}4)}}^{2}} - d{\text{/}}2c} \\ = (d{\text{/}}2c){\text{/}}({{u}_{2}}{\text{/}}4 + \sqrt {{{{({{u}_{2}}{\text{/}}4)}}^{2}} - d{\text{/}}2c} ). \\ \end{gathered} $$

Let us suppose that

$$\varepsilon {{u}_{2}}{\text{/}}2 = {{u}_{2}}{\text{/}}4 + \sqrt {{{{({{u}_{2}}{\text{/}}4)}}^{2}} - d{\text{/}}2c} ,\quad 1{\text{/}}2 \leqslant \varepsilon < 1.$$

Then,

$$(1 - \varepsilon ){{u}_{2}}{\text{/}}2 = {{u}_{2}}{\text{/}}4 - \sqrt {{{{({{u}_{2}}{\text{/}}4)}}^{2}} - d{\text{/}}2c} .$$

Consequently,

$$\varepsilon (1 - \varepsilon ){{({{u}_{2}}{\text{/}}2)}^{2}} = d{\text{/}}2c,$$

or, taking expressions (A.17) into account, we obtain

$$\varepsilon (1 - \varepsilon ) = \frac{{2d}}{{cu_{2}^{2}}} = \frac{{2{{{(1 - {v})}}^{2}}}}{{{{{(1 + {v})}}^{2}}}},$$

(A.22)

$${{u}_{2}} - {{u}_{ + }} = \frac{d}{{\varepsilon c{{u}_{2}}}}.$$

(A.23)

Substituting relations (A.22) and (A.23) into (A.21), we obtain

$$\begin{gathered} \frac{{\partial (m_{{bx}}^{2})}}{{\partial {v}}} = u_{ + }^{2}\left[ {{{{\left( {\frac{d}{{\varepsilon c{{u}_{2}}}}} \right)}}^{2}}\frac{{\partial c}}{{\partial {v}}} + \frac{{2d}}{{\varepsilon {{u}_{2}}}}\frac{{\partial {{u}_{2}}}}{{\partial {v}}} + \frac{{\partial d}}{{\partial {v}}}} \right] \\ = \frac{{u_{ + }^{2}d}}{\varepsilon }\left[ {(1 - \varepsilon )\frac{{\partial \ln (c)}}{{\partial {v}}} + \varepsilon \frac{{\partial \ln (d)}}{{\partial {v}}} + 2\frac{{\partial \ln ({{u}_{2}})}}{{\partial {v}}}} \right]. \\ \end{gathered} $$

(A.24)

Taking relations (A.17) into account, we obtain

$$\begin{gathered} \frac{\varepsilon }{{u_{ + }^{2}d}}\frac{{\partial (m_{{bx}}^{2})}}{{\partial {v}}} = (1 - \varepsilon )\left[ {\frac{1}{{1 - {v}}} + \frac{1}{{v}} + \frac{{v}}{{1 + {{{v}}^{2}}}}} \right] \\ + \,\varepsilon \left[ {\frac{2}{{v}} + \frac{{2{v}}}{{1 + {{{v}}^{2}}}}} \right] + \frac{2}{{1 + {v}}} - \frac{{4{v}}}{{1 + {{{v}}^{2}}}} \\ = \frac{{1 - \varepsilon }}{{1 - {v}}} + \frac{{1 + \varepsilon }}{{v}} + \frac{2}{{1 + {v}}} - \frac{{(3 - \varepsilon ){v}}}{{1 + {{{v}}^{2}}}} \\ \geqslant \frac{{1 + \varepsilon }}{{v}} + \frac{2}{{1 + {v}}} - \frac{{2{v}}}{{1 + {{{v}}^{2}}}} \geqslant \frac{{1 + \varepsilon }}{{v}} > 0. \\ \end{gathered} $$

Thus, we have proved that d($m_{{bx}}^{2}$)/d${v}$ > 0 on curve u = u₊ and, in particular, $m_{{bx}}^{2}$ decreases during the motion in the direction of arrows under the curve in Fig. 5.

Thus, $m_{{bx}}^{2}$ attains its minimum for x₁ = ${v}$ and x₂ = 1. Substituting these conditions into (A.8b), we obtain

$$m_{{bx}}^{2} = \frac{{{{{(2b - a)}}^{2}}}}{{{{{(1 - {v})}}^{2}}}} + \frac{{{{{(2b{v} - a)}}^{2}}}}{{{{{v}}^{2}}{{{(1 - {v})}}^{2}}}}.$$

(A.25)

The minimum of this relation can be found from the following equation:

$$\begin{gathered} {{P}_{b}}({v}) = ({{(2b - a)}^{2}} + 4{{b}^{2}}){{{v}}^{3}} - 6ab{{{v}}^{2}} \\ \, + (2ab + 2{{a}^{2}}){v} - {{a}^{2}} = 0. \\ \end{gathered} $$

(A.26)

$${{P}_{b}}(0) = - {{a}^{2}} < 0\quad {\text{and}}\quad {{P}_{b}}(1) = 2{{(2b - a)}^{2}} > 0,$$

for this reason, Eq. (A.26), as well as (A.16), has the same root on the interval 0 ≤ ${v}$ ≤ 1.

If b ≪ a ($\bar {\alpha }$ → πn, F_Z → 0 (see Fig. 2a); $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha }$ → arctan(1/2λ) + πn, and Y^C → 2λZ^C (see Fig. 2b), Eqs. (A.16) and (A.26) are transformed into

$$\left\{ \begin{gathered} {{P}_{a}}({v}) \to {{{v}}^{4}} + 2{v} - 1 = 0, \hfill \\ {{P}_{b}}({v}) \to {{{v}}^{3}} + 2{v} - 1 = 0. \hfill \\ \end{gathered} \right.$$

(A.27)

It should be noted that, in this limit, $m_{x}^{2}$ and $m_{y}^{2}$ are minimized at the same point.

If a ≪ b ($\bar {\alpha }$ → –arctanλ + πn, λF_Y → –F_Z (see Fig. 2a); $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha }$ → arctan(1/3λ) + πn, and Y^C → 3λZ^C (see Fig. 2b)), Eqs. (A.16) and (A.26) are transformed into

$$\left\{ \begin{gathered} {{P}_{a}}({v}) \to {v} = 0, \hfill \\ {{P}_{b}}({v}) \to {v} = 0. \hfill \\ \end{gathered} \right.$$

(A.28)

For arbitrary values of a and b, the equations for minimization of $m_{{ax}}^{2}$ and $m_{{bx}}^{2}$ are reduced to

$$\left\{ \begin{gathered} {{p}_{a}}({v}) = \frac{{{{P}_{a}}({v})}}{{4{{b}^{2}}}} = {{(1 - \delta )}^{2}}{{{v}}^{4}} + {{{v}}^{3}} - 3\delta {{{v}}^{2}} \hfill \\ + \,\delta (1 + 2\delta ){v} - {{\delta }^{2}} = 0, \hfill \\ {{p}_{b}}({v}) = \frac{{{{P}_{b}}({v})}}{{4{{b}^{2}}}} = ({{(1 - \delta )}^{2}} + 1){{{v}}^{3}} - 3\delta {{{v}}^{2}} \hfill \\ + \,\delta (1 + 2\delta ){v} - {{\delta }^{2}} = 0, \hfill \\ \end{gathered} \right.$$

(A.29)

where δ = a/2b, x₁ = ${v}$.

To minimize $m_{x}^{2}$ = cos²θ$m_{{ax}}^{2}$ + sin²θ$m_{{bx}}^{2}$, we must seek the root of the equation

$${{\cos }^{2}}\theta {{p}_{a}}({v}) + {{\sin }^{2}}\theta {{p}_{b}}({v}) = 0.$$

(A.30)

Let us also write the expansion of the solution to Eq. (A.29) in parameter δ = a/2b:

$$\left\{ \begin{gathered} {{p}_{a}}({v}) = 0,\quad {v} = \delta - {{\delta }^{3}} + {{\delta }^{4}}, \hfill \\ {{p}_{b}}({v}) = 0,\quad {v} = \delta - {{\delta }^{2}} + 4{{\delta }^{3}} - 18{{\delta }^{4}}. \hfill \\ \end{gathered} \right.$$

(A.31)

Minimization of relative errors

Let us minimize (σ_a/a)² + (σ_a/b)² = $\eta _{x}^{2}\sigma _{x}^{2}$, where $\eta _{x}^{2}$ = $m_{{ax}}^{2}$/a² + $m_{{bx}}^{2}$/b². Taking x = ${v}$ and δ = a/2b into account, we can write the condition for the minimum of relative error η_x:

$$\frac{{{{p}_{a}}({v})}}{{{{a}^{2}}}} + \frac{{{{p}_{b}}({v})}}{{{{b}^{2}}}} = 0.$$

(A.32)

or

$$\begin{gathered} {{(1 - \delta )}^{2}}{{{v}}^{4}} + (1 + 8\delta - 8{{\delta }^{2}} + 4{{\delta }^{3}}){{{v}}^{3}} - 3(1 + 4\delta ){{{v}}^{2}} \\ {\kern 1pt} + \delta (1 + 2\delta )(1 + 4\delta ){v} - {{\delta }^{2}}(1 + 4\delta ) = 0. \\ \end{gathered} $$

(A.33)

Quantities a and b have different signs.

The formal line of proof described above is applicable for simultaneously positive or simultaneously negative values of a and b. Let us consider the situation with different signs of a and b (we assume that x₁, x₂ ∈ [0; 1]).

The substitution x₁ = ${v}$x₂ = |a/2b|/u, which refines expressions (A.9), gives, instead of (A.10), (A.11), and (A.17), the following expressions differing only in the sign reversal of u₁ and u₂:

$$m_{{ax}}^{2}\sim {{c}_{1}}{{(u + {{u}_{1}})}^{2}} + {{d}_{1}},$$

(A.34)

$$m_{{bx}}^{2}\sim ({{c}_{2}}{{(u + {{u}_{2}})}^{2}} + {{d}_{2}}){{u}^{2}},$$

(A.35)

with the same dependences of c₁, c₂, d₁, d₂, u₁, and u₂ on ${v}$ as in relations (A.10) and (A.17). Expressions (A.34) and (A.35) as functions of u always decrease in the range of positive values of u. Consequently, in the minimization of $m_{x}^{2}$, the situation with u = |a/2b|/${v}$ is always realized as well; i.e., x_2(extr) = 1. Therefore, after the differentiation of relations (A.34) and (A.35) as functions of x₁ = ${v}$, we obtain the same equations as (A.16) and (A.26), which make it possible to find the sought roots ${v}$ on segment [0; 1]. Relations (A.29) and (A.33) also hold (now, only for δ ≤ 0). Limiting relations (A.27) and (A.28) hold, while expansion (A.31) is not important because it corresponds to negative x₁ = ${v}$ in the given case. Positive values of x₁ = ${v}$ are given by the following expansions in δ (δ < 0, |δ| ≪ 1):

$$\left\{ \begin{gathered} {{p}_{a}}({v}) = 0{\text{:}}\quad {v} \cong \sqrt {{\text{|}}\delta {\text{|}}} - \,{\text{|}}\delta {\text{|}}{\text{,}} \hfill \\ {{p}_{b}}({v}) = 0{\text{:}}\quad {v} \cong \sqrt {\frac{{{\text{|}}\delta {\text{|}}}}{2}} - \,\frac{{{\text{|}}\delta {\text{|}}}}{{2\sqrt 2 }}{\text{.}} \hfill \\ \end{gathered} \right.$$

(A.36)

Let us consider the case when a = 2b ($\bar {\alpha }$ → π(2n + 1)/2, F_Y = 0 (see Fig. 2a); $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha }$ → arctan(2/3λ) + πn, 2Y^C → 3λZ^C (see Fig. 2b)).

Substituting δ = 1 into relation (A.29), we obtain p_a(${v}$) = p_b(${v}$) = (1 – ${v}$)³, i.e., x₁ = x₂ = 1. We can verify that such a condition corresponds to the minimum of $m_{{ax}}^{2}$ and $m_{{bx}}^{2}$ by substituting relation u = 1/${v}$ (which follows from (A.9) for x₂ = 1 and a = 2b) into Eqs. (A.10) and (A.11). This yields the expressions

$$\left\{ \begin{gathered} m_{{ax}}^{2} = \frac{{{{a}^{2}}}}{{{{{v}}^{2}}}}, \hfill \\ m_{{bx}}^{2} = \frac{{2{{a}^{2}}}}{{1 + {{{v}}^{2}}}}, \hfill \\ \end{gathered} \right.$$

(A.37)

which indeed have a minimum for ${v}$ = 1; i.e., x₁ = x₂ = 1.

This result indicates that the exact optimal value in x₁ and x₂ cannot be found disregarding the contribution of $m_{y}^{2}$.

3.4. General Case

Let us consider the general case and (see also relation (A.5)). We minimize

$$m_{x}^{2}\sigma _{x}^{2} + m_{y}^{2}\sigma _{y}^{2},$$

(A.38)

where $m_{x}^{2}$ is taken from expressions (A.8a), (A.8b), and (A.8c) and $m_{y}^{2}$ is taken from (A.6b), and substitution x₁ = ${v}$ and x₂ = 1 is performed. If we establish the relation

$${{\sigma }_{y}} = k{{\sigma }_{x}},\quad k > 0,$$

(A.39)

we will have to minimize the following expression in ${v}$:

$$\frac{{({{{\cos }}^{2}}\theta {{{v}}^{2}} + {{{\sin }}^{2}}\theta )({{k}^{2}} + {{{(2b - a)}}^{2}}){{{v}}^{2}} + {{{(2b{v} - a)}}^{2}} + {{k}^{2}}}}{{{{{v}}^{2}}{{{(1 - {v})}}^{2}}}}.$$

(A.40)

Contributions of $m_{y}^{2}$ and $m_{x}^{2}$ prevail depending on the relation between k and |2b – a|. Accordingly, the conditions of minimum are close either to x_1(extr) ≅ 0.464 (large k) or to the roots of Eq. (A.16) or (A.26) (small k).

The minimum of expression (A.40), x₁ = ${v}$, lies in region 0 < ${v}$ < 1 as the root of the equation

$$\begin{gathered} P = {{\cos }^{2}}\theta [{{k}^{2}}({{{v}}^{4}} + 2{v} - 1) + {{P}_{a}}({v})] \\ + \,\,{{\sin }^{2}}\theta [{{k}^{2}}({{{v}}^{3}} + 2{v} - 1) + {{P}_{b}}({v})] = 0, \\ \end{gathered} $$

(A.41)

where P_a(${v}$) and P_b(${v}$) are taken from Eqs. (A.16) and (A.26).

When a = 2b, we have P_a(${v}$) = P_b(${v}$) = 4b²(1 – ${v}$)³ = a²(1 – ${v}$)³, and Eq. (A.41) is reduced to

$$\left\{ \begin{gathered} {\text{cos}}\theta \, = \,1,\,\,{\text{min}}(m_{a}^{2})\,:\,{{k}^{2}}({{{v}}^{4}}\, + \,2{v}\, - \,1)\, + \,{{a}^{2}}{{(1\, - \,{v})}^{3}}\, = \,0, \hfill \\ {\text{sin}}\theta \, = \,1,\,\,{\text{min}}(m_{b}^{2})\,:\,{{k}^{2}}({{{v}}^{3}}\, + \,2{v}\, - \,1)\, + \,{{a}^{2}}{{(1\, - \,{v})}^{3}}\, = \,0. \hfill \\ \end{gathered} \right.$$

(A.42)

The roots of these equations depend only on k/a (δ = 1).

The case of δ = 1 and arbitrary θ is described by the equation

$${{k}^{2}}({{\cos }^{2}}\theta {{{v}}^{4}} + {{\sin }^{2}}\theta {{{v}}^{3}} + 2{v} - 1) + {{a}^{2}}{{(1 - {v})}^{3}} = 0,$$

(A.43)

the roots of which weakly depend on θ.

The most general of Eqs. (A.41)–(A.43) is (A.41). Its root depends on δ = a/2b, k/a, and θ.

The condition of identical relative sensitivities (see Eq. (A.32)) means that

$${{\cos }^{2}}\theta = \frac{{{{b}^{2}}}}{{{{a}^{2}} + {{b}^{2}}}},\quad {{\sin }^{2}}\theta = \frac{{{{a}^{2}}}}{{{{a}^{2}} + {{b}^{2}}}}.$$

(A.44)

These relations can be used in Eq. (A.41). The solution will depend on a/2b and k/a.

In particular, for a = 2b, Eqs. (A.44) are transformed to cos²θ = 1/5 and sin²θ = 4/5. Substituting these relations into Eq. (A.32) for k/a, k/b ≪ 1 yields

$${{x}_{1}} = {v} \cong 1 - \sqrt[3]{{2{{k}^{2}}{\text{/}}{{a}^{2}}}} = 1 - \sqrt[3]{{{{k}^{2}}{\text{/}}2{{b}^{2}}}}.$$

(A.45)

For k = a = 2b, Eq. (A.42) has the following approximate roots:

$$\left\{ \begin{gathered} \min (m_{a}^{2}):{{x}_{1}} \cong 0.52, \hfill \\ \min (m_{b}^{2}):{{x}_{1}} \cong 0.50. \hfill \\ \end{gathered} \right.$$

(A.46)

Concluding this section, we write the expressions for P in (A.41) in the general case and in particular cases when a ≪ b or b ≪ a:

$$\begin{gathered} P = {{\cos }^{2}}\theta ({{k}^{2}} + {{(2b - a)}^{2}}){{{v}}^{4}} \\ \, + ({{\sin }^{2}}\theta ({{k}^{2}} + {{(2b - a)}^{2}}) + 4{{b}^{2}}){{{v}}^{3}} \\ \, - 6ab{{{v}}^{2}} + 2({{k}^{2}} + ab + {{a}^{2}}){v} - ({{k}^{2}} + {{a}^{2}}), \\ \end{gathered} $$

(A.47a)

$$\begin{gathered} \frac{{P{{{\text{|}}}_{{ba \ll b}}}}}{{4{{b}^{2}}}} \to {{\cos }^{2}}\theta \left[ {\frac{{{{k}^{2}}}}{{4{{b}^{2}}}}({{{v}}^{4}} + 2{v} - 1) + {{{v}}^{4}} + {{{v}}^{3}}} \right] \\ + {{\sin }^{2}}\theta \left[ {\frac{{{{k}^{2}}}}{{4{{b}^{2}}}}({{{v}}^{3}} + 2{v} - 1) + 2{{{v}}^{3}}} \right], \\ \end{gathered} $$

(A.47b)

$$\frac{{P{{{\text{|}}}_{{b \ll a}}}}}{{({{k}^{2}} + {{a}^{2}})}} \to ({{\cos }^{2}}\theta {v} + {{\sin }^{2}}\theta ){{{v}}^{3}} + 2{v} - 1.$$

(A.47c)

For k/b ≫ 1, the root of Eq. (A.47b) is ${v}$ = x_1(extr) ≅ 0.464; if k/b ≪ 1, we have ${v}$ ≅ 0. The root of Eq. (A.47c) is independent of k/a and is always close to ${v}$ = x_1(extr) ≅ 0.464.

3.5. Calculation of Auxiliary Parameter θ

The values of auxiliary parameter θ can be determined using relation (2) by minimizing $\sigma _{{{{F}_{Y}}}}^{2}$ + $\sigma _{{{{F}_{Z}}}}^{2}$ or $\sigma _{{{{Y}^{C}}}}^{2}$ + $\sigma _{{{{Z}^{C}}}}^{2}$ taking into account the mutual independence of errors in determining a and b. For the cantilever used in experiment with λ = 0.2, we describe the procedure for calculating $\bar {\theta }$,

$$\begin{gathered} \left\{ \begin{gathered} {{F}_{Y}} = \frac{{{{k}_{C}}{{l}_{C}}}}{{3\lambda }}(\bar {a} - 2\bar {b}), \hfill \\ {{F}_{Z}} = \frac{{2{{k}_{C}}{{l}_{C}}}}{3}\bar {b} \hfill \\ \end{gathered} \right.\, \to \,\left\{ \begin{gathered} \sigma _{{{{F}_{Y}}}}^{2} = \frac{{k_{C}^{2}l_{C}^{2}}}{{9{{\lambda }^{2}}}}(\sigma _{{\bar {a}}}^{2} + 4\sigma _{{\bar {b}}}^{2}), \hfill \\ \sigma _{{{{F}_{Z}}}}^{2} = \frac{{4k_{C}^{2}l_{C}^{2}}}{9}\sigma _{{\bar {b}}}^{2}, \hfill \\ \end{gathered} \right. \\ \sigma _{{{{F}_{Y}}}}^{2} + \sigma _{{{{F}_{Z}}}}^{2} \\ = \frac{{k_{C}^{2}l_{C}^{2}}}{{9{{\lambda }^{2}}}}(\sigma _{{\bar {a}}}^{2}\, + \,4(1\, + \,{{\lambda }^{2}})\sigma _{{\bar {b}}}^{2})\, \to \,{\text{co}}{{{\text{s}}}^{2}}\,\bar {\theta }\, \cong \,0.19, \\ {{\sin }^{2}}\bar {\theta } \cong 0.81; \\ \end{gathered} $$

(A.48)

as well as $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }$,

$$\begin{gathered} \left\{ \begin{gathered} {{Y}^{C}} = \lambda {{l}_{C}}(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} ), \hfill \\ {{Z}^{C}} = \frac{{{{l}_{C}}}}{6}(3\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} - 2\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} ) \hfill \\ \end{gathered} \right. \to \left\{ \begin{gathered} \sigma _{{{{Y}^{C}}}}^{2} = {{\lambda }^{2}}l_{C}^{2}(\sigma _{{\underline{a} }}^{2} + \sigma _{{\underline{b} }}^{2}), \hfill \\ \sigma _{{{{Z}^{C}}}}^{2} = \frac{{l_{C}^{2}}}{{36}}(9\sigma _{{\underline{a} }}^{2} + 4\sigma _{{\underline{b} }}^{2}), \hfill \\ \end{gathered} \right. \\ \sigma _{{{{Y}^{C}}}}^{2} + \sigma _{{{{Z}^{C}}}}^{2} = l_{C}^{2}(({{\lambda }^{2}} + 1{\text{/}}4)\sigma _{{\underline{a} }}^{2} + ({{\lambda }^{2}} + 1{\text{/}}9)\sigma _{{\underline{b} }}^{2}) \\ \to {{\cos }^{2}}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } \cong 0.66,\quad {{\sin }^{2}}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } \cong 0.34. \\ \end{gathered} $$

(A.49)