Boson Peak in Amorphous Graphene in the Stable Random Matrix Model

Abstract

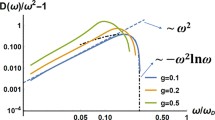
The effect of disorder in the distribution of force constants on optical and acoustic phonons in the scalar model of crystalline graphene is studied for both oscillations lying in the sheet plane and for flexural modes. It was shown that in the model of stable random matrices with translational symmetry, an additional to Debye vibrational density of states arises at a sufficient degree of disorder, i.e., the boson peak. The boson peak shifts to lower frequencies with increasing relative fluctuations of force constants and decreasing Young’s modulus of the system. At a weak disorder (or with no disorder), there are two peaks in the density of states g(ω), which correspond to logarithmic van-Hove singularity for acoustic and optical phonons of crystalline graphene. These peaks broaden and merge into a single boson peak with increasing disorder. Optical phonons are first destroyed due to disorder, while acoustic phonons gradually transform to the boson peak. For flexural modes there is a slightly different situation. Van-Hove singularities still spread disorder, but lead to the appearance of phonons in the system, which form the boson peak and move with it to low frequencies with increasing disorder.

APPENDIX

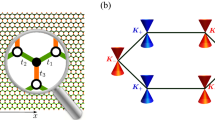
Let us consider separately coupled vibrations of “dark” and “light” graphene lattice atoms shown in Fig. 2, with amplitudes V_n, m and U_n, m, respectively. Subscripts n and m number the atomic position along translation vectors а₁ and a₂. Let κ₁ and κ₂ be elastic coupling constants of the atom with neighbors from the first and second coordination circles containing three and six atoms, respectively.

Considering atomic masses to be identical, we write their equations of motion

$$m\frac{{{{d}^{2}}{{U}_{{n,m}}}}}{{d{{t}^{2}}}} = {{\kappa }_{1}}({{V}_{{n,m}}} + {{V}_{{n - 1,m}}} + {{V}_{{n,m - 1}}} - 3{{U}_{{n,m}}})$$

$$ + \;{{\kappa }_{2}}({{U}_{{n + 1,m}}} + {{U}_{{n - 1,m}}} + {{U}_{{n,m + 1}}}$$

$$\begin{gathered} + \;{{U}_{{n,m - 1}}} + {{U}_{{n - 1,m + 1}}} + {{U}_{{n + 1,m - 1}}} - 6{{U}_{{n,m}}}), \\ m\frac{{{{d}^{2}}{{V}_{{n,m}}}}}{{d{{t}^{2}}}} = {{\kappa }_{1}}({{U}_{{n,m}}} + {{U}_{{n + 1,m}}} + {{U}_{{n,m + 1}}} - 3{{V}_{{n,m}}}) \\ \end{gathered} $$

(22)

$$ + \;{{\kappa }_{2}}({{V}_{{n + 1,m}}} + {{V}_{{n - 1,m}}} + {{V}_{{n,m + 1}}}$$

$$ + \;{{V}_{{n,m - 1}}} + {{V}_{{n - 1,m + 1}}} + {{V}_{{n + 1,m - 1}}} - 6{{V}_{{n,m}}}).$$

Let us seek the solution of Eq. (22) in the form of plane traveling perturbation waves with frequency ω and wave vector q,

$$\begin{gathered} {{U}_{{n,m}}} = {{U}^{0}}{{e}^{{i{\mathbf{q}}(n{{{\mathbf{a}}}_{1}} + m{{{\mathbf{a}}}_{2}}) - i\omega t}}}, \\ {{V}_{{n,m}}} = {{V}^{0}}{{e}^{{i{\mathbf{q}}(n{{{\mathbf{a}}}_{1}} + m{{{\mathbf{a}}}_{2}}) - i\omega t}}}. \\ \end{gathered} $$

(23)

After substituting Eq. (23) into the equations of motion (22), we obtain

$$\begin{gathered} - m{{\omega }^{2}}{{U}_{{n,m}}} = {{\kappa }_{1}}({{V}_{{n,m}}}A( - {\mathbf{q}}) - 3{{U}_{{n,m}}}) \\ + \;2{{\kappa }_{2}}{{U}_{{n,m}}}(f({\mathbf{q}}) - 3), \\ - m{{\omega }^{2}}{{V}_{{n,m}}} = {{\kappa }_{1}}({{U}_{{n,m}}}A{\text{*}}( - {\mathbf{q}}) - 3{{V}_{{n,m}}}) \\ + \;2{{\kappa }_{2}}{{V}_{{n,m}}}(f({\mathbf{q}}) - 3), \\ \end{gathered} $$

(24)

where the functions

$$A({\mathbf{q}}) = (1 + {{e}^{{i{{{\mathbf{a}}}_{1}}{\mathbf{q}}}}} + {{e}^{{i{{{\mathbf{a}}}_{2}}{\mathbf{q}}}}}),$$

(25)

$$f({\mathbf{q}}) = \cos ({{{\mathbf{a}}}_{1}}{\mathbf{q}}) + \cos ({{{\mathbf{a}}}_{2}}{\mathbf{q}})\cos (({{{\mathbf{a}}}_{1}} - {{{\mathbf{a}}}_{2}}){\mathbf{q}})$$

(26)

are introduced.

Having introduced the notations $\Omega _{{\,1}}^{2}$ = κ₁/m and $\Omega _{{\,2}}^{2}$ = κ₂/m and conditionally admitting that $\Omega _{{\,2}}^{2}$ can be negative, we rewrite system (24) in the form

$$\begin{gathered} {{U}_{{n,m}}}({{\omega }^{2}} - 3\Omega _{{\,1}}^{2} - 2\Omega _{{\,2}}^{2}(3 - f({\mathbf{q}})) + {{V}_{{n,m}}}\Omega _{{\,1}}^{2}A({\mathbf{q}}) = 0, \\ {{V}_{{n,m}}}({{\omega }^{2}} - 3\Omega _{{\,1}}^{2} - 2\Omega _{{\,2}}^{2}(3 - f({\mathbf{q}})) + {{U}_{{n,m}}}\Omega _{{\,1}}^{2}A{\text{*}}({\mathbf{q}}) = 0. \\ \end{gathered} $$

(27)

Equations (27) have a nontrivial solution provided the equal-zero determinant

$$({{\omega }^{2}} - 3\Omega _{{\,1}}^{2} - 2\Omega _{{\,2}}^{2}{{(3 - f({\mathbf{q}}))}^{2}} - \Omega _{{\,1}}^{4}A({\mathbf{q}})A{\text{*}}({\mathbf{q}}) = 0.$$

(28)

After transforming cofactors in the second term,

$$A({\mathbf{q}})A{\text{*}}({\mathbf{q}}) = 3 + 2f({\mathbf{q}}),$$

(29)

we obtain the formula for the dispersion relation of flexural modes in graphene taking into account two coordination circles,

$${{\omega }^{2}}({\mathbf{q}}) = \Omega _{{\,1}}^{2}(3 \pm \sqrt {3 + 2f({\mathbf{q}})} ) + 2\Omega _{{\,2}}^{2}(3 - f({\mathbf{q}})).$$

(30)

The “critical” relation of elastic constants κ₁ and κ₂ can be obtained from the condition of vanishing frequency (30) in the limit of small values aq $\ll$ 1 for the acoustic branch. Optical branch frequencies are always nonzero; therefore, this condition does not matter for them. To a first approximation, the function f(q) is given by

$$f({\mathbf{q}}) \approx 3 - \frac{9}{4}{{a}^{2}}{{q}^{2}} + \frac{{27}}{{64}}{{a}^{4}}{{q}^{4}}.$$

(31)

In this case, the acoustic branch frequency is given by the relation

$$\omega \,({\mathbf{q}}) \approx \frac{3}{4}(\Omega _{{\,1}}^{2} + 6\Omega _{{\,2}}^{2}){{a}^{2}}{{q}^{2}} - \frac{3}{{64}}(\Omega _{{\,1}}^{2} + 18\Omega _{{\,2}}^{2}){{a}^{4}}{{q}^{4}}.$$

(32)

At the relation of elastic constants κ₂ = –κ₁/6, κ₂ < 0, the term quadratic in q in Eq. (32) disappears, which yields the dispersion relation of flexural modes,

$$\omega ({\mathbf{q}}) \approx \frac{3}{4}(\Omega _{{\,1}}^{2} + 6\Omega _{{\,2}}^{2}){{a}^{2}}{{q}^{2}} - \frac{3}{{64}}(\Omega _{{\,1}}^{2} + 18\Omega _{{\,2}}^{2}){{a}^{4}}{{q}^{4}}.$$

(33)

It is easy to understand physically. At critical elastic coefficients, κ₂ = –κ₁/6, Young’s modulus of the graphene film for flexural modes is zero. Flexural modes phonons cannot propagate in such a soft medium, where their elastic modulus and speed of sound are zero. They are alternated by flexural modes waves with the other more complex dispersion relation. Near the critical state, this can phenomenologically be written as

$${{\omega }^{2}}({\mathbf{q}}) = a{{q}^{2}} + \beta {{q}^{4}},$$

(34)

where α ∝ κ₂ + κ₁/6, and β ~ 1. At the flexural modes transition point, α = 0. From this it follows that these vibrations are phonons with a linear dispersion relation at low frequencies ω < $\sqrt \alpha$, and the speed of sound ${v}$ ∝ $\sqrt \alpha$ vanishes at the critical point. At higher frequencies, these are flexural modes waves with quadratic dispersion relation. It should be noted that the disappearance of the term quadratic in q in the dispersion relation (32) is possible only when considering farther negative bonds.

In the case of the interaction only with neighbors from the first coordination circle (which is equivalent to the condition κ₂ = 0), Eq. (30) is reduced to the relation

$$\omega _{1}^{2}({\mathbf{q}}) = \Omega _{{\,1}}^{2}(3 \pm \sqrt {3 + 2f({\mathbf{q}})} ).$$

(35)

Let us show that the dispersion relation of flexural modes ω_f (q) corresponds to ω²(q). To this end, we transform Eq. (30) taking into account the “critical” relation of elastic constants κ₂ = –κ₁/6 as follows

$$\begin{gathered} \omega _{f}^{2}({\mathbf{q}}) = \Omega _{{\,1}}^{2}\left( {2 \pm \sqrt {3 + 2f({\mathbf{q}})} + \frac{{f({\mathbf{q}})}}{3}} \right) \\ = \frac{{\Omega _{{\,1}}^{2}}}{6}{{(3 \pm \sqrt {3 + 2f({\mathbf{q}})} )}^{2}} = \frac{1}{{6\Omega _{{\,1}}^{2}}}\omega _{1}^{4}({\mathbf{q}}). \\ \end{gathered} $$

(36)

In other words, the dispersion relation of flexural modes (36) can be defined as the squared phonon dispersion relation (35) taking into account the first coordination circle. In turn, this substantiates our choice of the dynamic matrix of flexural modes ${{\hat {C}}_{f}}$, defined as the squared dynamic matrix of planar vibrations ${{\hat {C}}_{p}}$.

Thus, the involvement of the interaction with atoms from the second coordination circle drastically changes the dispersion relation of graphene vibrational modes and, in the case of the “critical” relation of elastic constants, results in the quadratic dependence instead of the linear dispersion relation following from their interaction with atoms of the first coordination circle. We cannot answer the question what is the actual dispersion relation of flexural modes in graphene. It depends on the relation of elastic constants κ₁ and κ₂ which should be determined either experimentally or from a deeper theory. For example, if the consideration is based on experiments, the experimental points in Fig. 3 suggest that we are either in a critical situation or very close to it. This is clear from the parabolic appearance of the dispersion relation (it is obvious that more comprehensive processing of experimental data is required). We come to the same conclusion after an analysis of the theoretical data shown in Fig. 5. There is also clearly seen the nonlinear dependence ω(q) at the point Γ for ZA-type flexural modes. However, the authors of this study admit that they obtained a quadratic dependence by nulling the speed of sound. Flexural modes behave similarly in the present study. At the critical point, Young’s modulus and the speed of sound vanish in the present study as well. It is clear that a more comprehensive study of this problem is required to prove the existences of negative springs in graphene and the dispersion relation q².