Cumulative ${\pi}$-Mesons in ${}^{{12}}{C}{+}{}^{{9}}$Be-Interactions at 3.2 GeV/Nucleon

Abstract

In the FRAGM experiment at the heavy-ion accelerator$-$accumulator complex ITEP$-$TWA, yields of cumulative charged $\pi$ mesons have been measured in a fragmentation of carbon ions with the energy of 3.2 GeV/nucleon on a beryllium target. The momentum spectra of $\pi$ mesons cover four orders of the invariant cross section magnitude. They demonstrate the exponential fall with increasing energy. The measured inverse slope parameter is compared with similar measurements in nucleon–nucleus interactions and ion–ion collisions at lower energies. The energy dependence of the ratio of the yields of negative to positive $\pi$ mesons is presented. This dependence is discussed in a connection with Coulomb and isotopic effects. The obtained data are compared with predictions of several ion–ion interaction models.

1 INTRODUCTION

An understanding of mechanisms of cumulative processes [1, 2], kinematically forbidden in interactions of free nucleons, remains the unsolved problem of relativistic nuclear physics for many decades. Proposed hypotheses range from a formation of multi-quark clusters [3] in a nuclear matter to effects of multiple scattering of the particles in intranuclear cascade [4, 5]. Most of the experimental data on the cumulative processes were obtained in nucleon–nucleus interactions. A usage of ion–ion interactions extends the domain of investigations of these processes and may indicate the ways of solving this problem. Currently a large attention is paid to a phenomenologically accurate description of nucleus–nucleus interactions. In this direction, a significant amount of simulation codes of nucleus–nucleus interactions was developed. These codes require both an experimental validation and an improvement of their basic approaches. A testing of these models on the cumulative processes will allow to estimate their applicability to describe a wide range of kinematic distributions. A production of $\pi$ mesons, including cumulative ones, is the main inelastic process at intermediate energies. This production occurs mainly through multiple mesonic and baryonic resonances. The testing of the mentioned models on $\pi$ meson productions allows also a reliable control whether a production of intermediate resonances is correctly taken into account. This is one of the aims of the FRAGM experiment [6] at the multi-purpose heavy ion accelerator complex ITEP–TWA.

In this paper $\pi$ meson yields at a carbon ion fragmentation are compared with the predictions of four widely used ion–ion interaction models: Binary Cascade (BC) [7], Intra Nuclear Cascade Liege (INCL) [8], Quantum Molecule Dynamics (QMD) [9], and Los Alamos Quark Gluon String Model (LAQGSM) [10]. The first three models are in free access within the Geant4 [11, 12] package, supported by CERN. We made calculations with these models using the Geant4.10.5 version. The last model is supported and developed in the Los-Alamos laboratory (LANL) at USA. The LAQGSM model is a base of the transport code MCNP6 [13]. All aforementioned models treat nucleus–nucleus interactions as a sequence of general processes which include intranuclear cascade, production of excited prefragments and their deexcitation through Fermi breakup, fission and evaporation. However, a concrete implementations of these steps in these models are different. The description of these differences are far beyond the scope of this paper. The useful information on this topic can be found in the Geant4 Physics Manual [14].

2 THE EXPERIMENT

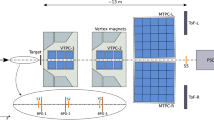
The FRAGM experiment studied the carbon fragmentation on an internal beryllium target of the ITEP accelerator

$${}^{12}\textrm{C}+^{9}\textrm{Be}\rightarrow f+X,$$

(1)

where $f$ is a fragment. For a simplicity the word ‘‘fragment’’ will include also $\pi$ mesons throughout this paper. The experimental setup was based on two-stage beam-line spectrometer that was placed at the angle of 3.5${}^{\circ}\pm 0.5^{\circ}$ with respect to the internal ion beam of the accelerator. A narrow vertical 50 micron-thick Be foil was used as a target. This allowed to have simultaneously a high luminosity by means of a multiple passage of ions through the target and a small size of the source for full usage of high momentum resolution of the spectrometer. The telescope consisting of three scintillation counters was used as a monitor that was directed to the target at the angle of 2${}^{\circ}$. In the first and second foci of the beam-line spectrometer, scintillation counters, which were used for amplitude and time-of-flight measurements, were located. Fragments were identified on correlation plots: amplitude (function of fragment charge) versus time-of-flight (function of fragment mass). For additional identification of $\pi$ mesons a threshold Cherenkov counter, placed at the second focus, was used. Detailed description of the setup is given in [6]. At each ion energy, the fragment yields were measured by scanning by the beam-line spectrometer rigidity with a step of 50–200 MeV/c. The momentum acceptance of the spectrometer was ${\pm}1.5\%$. Data were collected at a few kinetic energies of the ions in the range of 0.3–3.2 GeV/nucleon. Results on fragment yields were published in [15–18] for 0.3, 0.6, 0.95, and 2 GeV/nucleon, respectively. Below we will discuss only data obtained at a carbon ion energy of 3.2 GeV/nucleon. An example of an identification of the fragments is given in Fig. 1 for the rigidity of the beam-line spectrometer of 3.0 GeV/c. A good identification of all detected nuclear fragments: protons, deuterons, tritons, and ${{}^{3}}$He, as well as a good separation of protons from $\pi^{+}$ mesons at this momentum is seen. This $\pi$ meson identification method was used up to 3.0 GeV/c. At larger momenta a proton background was rejected by means of the signal from a gas threshold Cherenkov counter filled with freon-12 under the pressure of 2 atm. At this pressure the threshold for $\pi$ mesons was 2.0 GeV/c while for protons it was 14.0 GeV/c. The region near 3.0 GeV/c, where $\pi$ mesons were still identified without the Cherenkov counter, was used to calculate a small correction factor for $\pi$ meson absorption in the materials of this counter. This was done by the measurements with and without the counter in the beam-line.

Fig. 1

Identification of $\pi^{+}$ mesons on the two-dimensional distribution at the momentum 3.0 GeV/c: channels of the charge-to-digital converter (function of fragment charge) versus channels of the time-to-digital converter (function of fragment mass).

Figure 2 shows that the Cherenkov counter rejects the proton background by a factor of one thousand. It gives the possibility to measure a momentum dependence of the $\pi^{+}$ meson yield up to 5.2 GeV/c by fitting the time-of-flight distributions. The measurement of the $\pi$ mesons was performed without the Cherenkov counter by changing the polarity of a magnetic field in all elements of the beam-line spectrometer. The set-up efficiency was calculated by passing the fragments through beam-line spectrometer using the Geant4 package. A multiple scattering, ionization losses and nuclear interactions in the detector materials were taken into account. For $\pi$ mesons, their decays and registration of the decay products in the detectors were also taken into account.

Fig. 2

$\pi^{+}$ meson separation from the proton background with time-of-flight measurements at 3.4 GeV/c using the suppression of protons by the threshold Cherenkov counter (shaded region).

3 PROTON AND $\pi$ MESON MOMENTUM SPECTRA

Measured double differential cross sections for the yield of protons and $\pi^{-}$ mesons at an angle of 3.5${}^{\circ}$, $d^{2}\sigma/dpd\Omega$, in the laboratory frame are given in Fig. 3 along with the predictions of the four models of ion–ion interactions. Results for $\pi^{+}$ mesons are not shown because in logarithmic scale they look almost undistinguishable from those for $\pi^{-}$ mesons. They will only be used below in connection with the ratio of the yields of $\pi^{-}$ and $\pi^{+}$ mesons. Statistical errors of the measurements and calculations are mostly smaller than the size of symbols in Fig. 3. Only at maximal momenta of $\pi^{-}$ mesons they become visible. This is due to a high statistics of simulated events which was ten million per each model. To obtain the differential cross sections in the models, it was necessary to set the value of the total inelastic cross section of carbon ions with beryllium target. This value is directly calculated only within the LAQGSM model. It agrees with an accuracy of 7$\%$ with the phenomenological parameterization [19] and is equal to 834 mb for the carbon ion kinetic energy of 3.2 GeV/nucleon. This value was used for all the models. Since in our experiment the absolute cross sections are not measured, and the yields are measured in relation to the monitor, then, as in our previous works [18, 20], the normalization of the proton spectrum was carried out to the predictions of the models in the region of the proton fragmentation peak at about 4 GeV/c. In this region all the models predict similar values of the double differential cross sections which make it possible to estimate the error of this normalization procedure at 20$\%$. All the models, except the QMD, describe well also the shape of the proton fragmentation peak. The QMD narrows it down a lot. For the $\pi^{-}$ meson momentum spectra discrepancies between the predictions of the models are much larger. However, all the models predict close to exponential decrease of the cross section with an increase of $\pi$ meson momentum, but with different slope parameters. In Fig. 3, the arrow marks the boundary of the cumulative region. In fact, this is the maximum momentum of a $\pi^{+}$ meson produced at an angle of 3.5${}^{\circ}$ in the laboratory frame in the reaction $p+p\rightarrow d+\pi^{+}$. Production of $\pi$ mesons with larger momentum in collisions of free nucleons is forbidden by the energy/momentum conservation. It is interesting to note that the BC model describes almost ideally the experimental data from 1.5 to 4.8 GeV/c. At lower momenta, the data indicate flattening of the momentum dependence of the cross section that matches the INCL and LAQGSM model predictions, while the BC and QMD models predict the cross section decrease with the decrease of a $\pi$ meson momentum.

Fig. 3

Distributions of protons and $\pi^{-}$ mesons by the laboratory momentum ($p$) in comparison with the predictions of the four models of ion–ion interactions. The arrow shows the boundary of the cumulative region.

4 $\pi$ MESONS IN THE PROJECTILE REST FRAME

In the FRAGM experiment a nuclear fragmentation is studied in the so-called inverse kinematics when high energy fragments of a projectile nucleus are detected. This method has some advantages over the fragmentation measurements in the target rest frame. In the inverse kinematics, it is possible to measure fragments which are at rest in the projectile rest frame, and due to relativistic compression a larger angular acceptance is achieved . It is equally applies to $\pi$ mesons. However, when analyzing cumulative processes, the rest frame of a projectile nucleus is usually used. In this frame our data are presented in Fig. 4.

Fig. 4

$\pi^{-}$ meson distribution by the kinetic energy ($T_{rf}$) in the rest frame of a carbon nucleus in a comparison with the predictions of the four models of ion–ion interactions.

The abscissa shows the $\pi$ meson kinetic energy, the ordinate—the invariant cross section, $\sigma_{inv}=(E/p^{2})d^{2}\sigma/(dpd\Omega)$, where $E$ and $p$ are total energy and $\pi$ meson momentum, respectively. In this frame, the projectile is the beryllium nucleus, and the $\pi$ meson is emitted into the rear hemisphere with respect to the projectile. The angle of $\pi$ meson emission in this frame is a function of the $\pi$ meson momentum in the laboratory frame for the fixed angle in the laboratory frame (in our experiment it is equal to 3.5${}^{\circ}$ $\pm$ 0.5${}^{\circ}$). This dependence is given in Fig. 5. Vertical lines show the angular acceptance of our setup which is about $\pm 5^{\circ}$ in the rest frame of the carbon nucleus. It can be seen that for a laboratory frame momentum greater than 2 GeV/c (this corresponds to the kinetic energy of 125 MeV in the rest frame of a carbon nucleus) the $\pi$ meson angle is equal to 150${}^{\circ}$ and does not depend on the $\pi$ meson momentum. A characteristic feature of cumulative processes is a weak dependence on this angle near 180${}^{\circ}$, which allows to compare our data with those obtained in another experiments in the angular range 150${}^{\circ}$–180${}^{\circ}$. In Fig. 4 a comparison is made with the predictions of four models of ion–ion interactions. All models predict a close to exponential decrease of $\pi$ meson differential cross sections with an increase of their energy. To fit this energy dependence the function

Fig. 5

Dependence of the emission angle ($\theta$) on the $\pi$ meson kinetic energy ($T_{rf}$) in the rest frame of the carbon nucleus for the emission angle in the laboratory frame. Vertical lines stand for the angular acceptance of the FRAGM setup.

$$\sigma_{\textrm{inv}}=(E/p^{2})d^{2}\sigma/(dpd\Omega)$$

$${}=A\textrm{exp}(-T_{rf}/T_{c}),$$

(2)

was used, where $T_{rf}$ is the $\pi$ meson kinetic energy in the carbon ion rest frame, $T_{c}$ is a cumulative temperature or an inverse slope parameter. Here $A$ and $T_{c}$ are free parameters. For energies above the boundary of the cumulative region, marked with an arrow in Fig. 4, the fit gives the value of $T_{c}=51\pm 1$ MeV for the experimental data, 51 $\pm$ 1.5 MeV for the BC model, 43 $\pm$ 5 MeV for the INCL model, 40 $\pm$ 5 MeV for the LAQGSM model and 38 $\pm$ 17 MeV for the QMD model. Deterioration in the fit accuracy for some models is associated with a decrease in the fit range due to a sharper drop of the predicted cross sections. Figure 4 also shows that the boundary of the cumulative region does not affect the overall shape of the energy dependence of the $\pi$ meson yield. Indeed, the fit in the energy range 0.1–0.25 GeV of the experimental data, i.e. at energies not kinematically forbidden for the production of $\pi$ mesons in nucleon–nucleon interactions, gives $T_{c}=46.5\pm 2$ MeV, which is (within two standard deviations) consistent with $T_{c}$ obtained in the cumulative region. It differs strongly from the behavior of $T_{c}$ for cumulative protons, where near the boundary of the cumulative region $T_{c}$ is 7–9 MeV, compatible with the Fermi energy of the motion of nucleons in the fragmenting nucleus, while in the deep cumulative region $T_{c}$ is close to 50 MeV at energies of the incident nucleus, greater than several gigaelectronvolts (see, for example, [16, 18]). This can be an indication that the $\pi$ meson production mechanism does not undergo changes when crossing the boundary of the cumulative region. In all the aforementioned models of ion–ion interactions such a mechanism is Fermi breakup. In general terms, it looks like as follows. After the end of the intranuclear cascade, the excited nuclear matter disintegrates into prefragments, in which the total energy is statistically distributed between all possible combinations of fragments and particles. Wherein the distribution (2) naturally arises which is the Maxwell–Boltzmann distribution characterizing energy distribution of particles from a source with a certain temperature. Phenomenologically, this mechanism is close to hypothetical flucton and cluster mechanisms of the formation of cumulative particles. Of course, characteristic parameters of this mechanism are different in different models. They are largely based on a phenomenology, i.e. on obtaining a better description of a wide range of experimental data on ion–ion and nucleon–nucleus interactions. The results of the FRAGM experiment supplement the existing few data on the study of cumulative $\pi$ mesons in ion–ion interactions. These data on the energy dependence of the $T_{c}$ parameter in C $+$ C- and C $+$ Be-interactions are shown in Figure 6 together with data on $p+\textrm{C}$ interactions. The $T_{c}$ parameter in $p+\textrm{C}$ interactions was measured in the wide energy range of incident proton from 700 MeV to 400 GeV. These data demonstrate the rise of the $T_{c}$ parameter from 25 to 55 MeV in the energy range from 700 MeV to a few gigaelectronvolts and a constant value of the $T_{c}$ at higher energies (called as a nuclear scaling). The data on C $+$ C- and C $+$ Be-interactions show similar behavior. The $T_{c}$ parameter increases from 33 to 51 MeV in the energy range 1–3.2 GeV/nucleon. The measurement at maximal energy (19.6 GeV/nucleon) has been recently made at the FODS setup at IHEP [28, 29] in C $+$ C-interactions at 0${}^{\circ}$. With the consent of this group, we used this data to extract the cumulative temperature and obtained $T_{c}=48.4\pm 0.7$ MeV. This result can be regarded as an indication that the scaling behavior is also observed in ion–ion interactions.

Fig. 6

The dependence of the $\pi$ meson cumulative temperature ($T_{c}$) on the kinetic energy ($T$) of the incident nucleus: for proton-nucleus collisions (triangles: 0.73 GeV [21], 0.8–4.89 GeV [22, 23], 6.0 and 8.5 GeV [24], 15–65 GeV [25], 400 GeV [26]) and for the carbon fragmentation on carbon and beryllium targets (open circles: 1.05 and 2.1 GeV/nucleon [27], 3.2 GeV/nucleon—this experiment, 19.6 GeV/nucleon [28]).

5 THE RATIO OF YIELDS OF $\pi^{-}$ AND $\pi^{+}$ MESONS

As was mentioned above, in the FRAGM experiment the yields of both $\pi^{-}$ and $\pi^{+}$ mesons were measured. For $\pi^{-}$ mesons, their maximal momentum was limited only by statistics, while for $\pi^{+}$ mesons the limit was connected with the possibility to separate them from a proton background using time-of-flight measurements and the threshold Cherenkov counter. So $\pi^{+}$ mesons were measured up to 5.2 GeV/c in the laboratory frame while for $\pi^{-}$ mesons the maximal momentum was 5.4 GeV/c. At largest momenta, the accuracy of the measurement was defined by statistics of detected events only. At lower momenta, this accuracy was determined mainly by the monitor stability, which was at 5$\%$ level. The dependence of the ratio of yields of $\pi^{-}$ and $\pi^{+}$ mesons on their momenta in the laboratory frame is shown in Fig. 7 along with predictions of the BC, INCL, and LAQGSM models. The measurement of this ratio in the cumulative region represents undoubted interest since it carries information about the isotopic structure of yet unidentified mechanism of the cumulative $\pi$ meson emission. In proton–carbon interactions the $\pi^{-}/\pi^{+}$ ratio integrated over $T_{rf}$ from 100 MeV increases from 0.31 $\pm$ 0.13 to 0.78 $\pm$ 0.12 in the proton energy range from 0.8 to 4.89 GeV [23], while at higher energies 15–65 GeV [25] it is compatible with unity within about 20$\%$ uncertainty for all energies both for $\pi$ mesons and protons. This dependence is explained by a rise of $\pi^{-}$ production cross section with an increase of proton energy because in $pp$-interactions it is possible only through pair production of $\pi$ mesons. In nucleus–nucleus collisions a contribution of isotopic effects is expected to be significantly smaller. So, in [23] the integrated $\pi^{-}/\pi^{+}$ ratio mentioned above is compatible with unity within 20$\%$ uncertainty for a wide set of combinations of a beam ion and a target nucleus in the energy range 1.05–2.1 GeV/nucleon. This ratio is defined by both isotopic and Coulomb effects. Interaction with an isotope-asymmetric beryllium nucleus can lead to a value of this ratio somewhat greater than unity and be independent of the energy of $\pi$ meson. The influence of Coulomb forces leads to an increase of $\pi^{+}$ meson energy and to a decrease of $\pi^{-}$ meson energy. In case of a fast decrease of $\pi$ meson yields with energy this will lead to the $\pi^{-}/\pi^{+}$ ratio less than unity. Let us estimate approximately this effect in the rest frame of a carbon nucleus using the mean potential energy of a charged $\pi$ meson in a carbon nucleus as $dT=6eZ/(5R)$, where $e=1/137$, $Z=6$ is a charge and $R=2.97$ fm is a radius of a carbon nucleus. This gives $dT=3.5$ MeV and the ratio $\pi^{-}/\pi^{+}=1-2dT/T_{c}=0.86$. Within errors, this is compatible with our measurements that give a slightly smaller value, and with the INCL model predictions for $\pi$ meson momenta greater than 2 GeV. The experimental data show a rise of the $\pi^{-}/\pi^{+}$ ratio with the decrease of the $\pi$ meson momentum in a good agreement with the prediction of the BC model and to a lesser extent with the INCL model prediction. This increase can be associated with the so-called ‘‘spectator’’ effect, for the first time observed in the experiments at the LBL in Berkeley [30, 31] in the fragmentation of light ions at 0${}^{\circ}$ at energies of several hundred MeV/nucleon and later seen in the NA49 and NA61/SHINE experiments at the SPS CERN in peripheral collisions of lead ions at 150 GeV/nucleon and small (${\leq}100$ MeV/c) $\pi$ meson transverse momenta (for a review of these data, see [32]). A theoretical explanation of this effect was given in [33] back in 1982, but the processes, associated with this Coulomb effect in interactions of relativistic heavy ions, are widely discussed at the present time (see, e.g., [34]). Qualitatively this ‘‘spectator’’ effect, manifested only in peripheral collisions, is explained by focusing of negatively charged particles, emitted from a spectator region at small angles with velocities close to the spectator velocity, and by defocusing of positively charged particles. The $\pi^{-}/\pi^{+}$ ratio reaches a maximum exceeding 20, at $\pi$ meson velocities equal to that of a spectator and at zero angle. This ratio decreases with increasing both the $\pi$ meson emission angle (or the transverse momentum) and the difference between $\pi$ meson and spectator velocities. In our experiment the velocities of $\pi$ meson and a spectator (its velocity is approximately equal to a velocity of the carbon ion) coincide at the $\pi$ meson momentum of about 600 MeV/c. Unfortunately, due to technical problems to set low currents in magnetic elements of the beam-line spectrometer, only momenta which exceed 1 GeV/c were available for measurements. Nevertheless, the observed rise of the $\pi^{-}/\pi^{+}$ ratio to the value of 1.5 with decreasing momentum up to 1 GeV/c can be a manifestation of the spectator effect. It is also worth noting here that the $\pi^{-}/\pi^{+}$ ratio in the low-energy region of $\pi$ mesons is a sensitive test of the interaction mechanisms used in these models.

Fig. 7

The $\pi^{-}/\pi^{+}$ ratio as a function of the $\pi$ meson momentum ($p$) in the laboratory frame in comparison with the predictions of models of ion–ion interactions.

6 CONCLUSIONS

In the FRAGM experiment, the $\pi^{+}$ and $\pi^{-}$ meson yields at the angle of 3.5${}^{\circ}$ were measured in the fragmentation of carbon nuclei with the energy of 3.2 GeV/nucleon on beryllium target. These are the first measurements at such a high energy in an isotopically asymmetric combination of beam and target nuclei. The $\pi$ meson kinetic energy spectra in the rest frame of the incident carbon nucleus are well described by an exponent with the inverse slope parameter or the cumulative temperature $T_{c}=51\pm 1$ MeV. It is shown, that the transition from the region, where the $\pi$ meson production on a free nucleon is kinematically allowed, to the cumulative region does not change the value of this parameter. These spectra were compared with the predictions of four models of ion–ion interactions: BC, INCL, LAQGSM, and QMD. All models predict close to exponential decrease of the differential cross section of $\pi$ meson yields. However, only the BC model provides a good description of the experimental data. The obtained value of $T_{c}$ complements existing data on its dependence on the energy of an incident nucleus, confirming the $T_{c}$ rise in the energy range from 1 to 3.2 GeV/nucleon. Together with the new data from the FODS experiment [29] at an energy of 19.6 GeV/nucleon [28] our result indicates the independence of the $T_{c}$ parameter for projectile energies above 3.2 GeV/nucleon. This energy dependence is like well measured in proton–nucleus collisions in the energy range from 0.7 to 400 GeV. Also in the FRAGM experiment, the ratio of $\pi^{-}$ and $\pi^{+}$ yields was measured as well as its dependence on their energy. This ratio is sensitive to such subtle effects as the influence of isotopic symmetry and Coulomb forces. At high $\pi$ meson energies the data are in a satisfactory agreement with the influence of Coulomb forces leading to this ratio less than unity. At low energies, where the ratio increases with decreasing energy and becomes larger than unity, this rise indicates the manifestation of the ‘‘spectator’’ mechanism, which was observed earlier only in a few experiments both at smaller energy in the LBL and at much higher energies at the SPS. The BC model describes this rise well. The discrepancy with the predictions of other models indicates the sensitivity of this ratio to the mechanisms of ion–ion interactions used in these models.