1. INTRODUCTION

The issues of droplet evaporation have attracted significant attention both from the theory point of view and in connection with the development of new applications, including pattern formation on surfaces, preparation of ultra-clean surfaces, deposition of microarrays of DNA and RNA molecules, protein crystallography, combustion of fuel droplets in engine, diagnosis of diseases, development of modern printing methods for inkjet printers, manufacture of new electronic and optical devices and a number of other areas [1–6].

The nonuniform mass flow and heat transfer during a drop evaporation have a crucial influence on the evaporation kinetics. In particular, they change the temperature distribution along the droplet surface and can cause thermocapillary convection inside the droplet due to the temperature-dependent surface tension. Axisymmetric Marangoni flows can often be observed at room temperature and under atmospheric pressure [7–10].

A thermocapillary fluid flow with the broken axial symmetry can spontaneously appear inside a substantially heated droplet with an intense evaporation and sufficiently high fluid velocity. In a heated droplet, a Marangoni instability due to non-uniform temperature distribution can lead to the fluid motion of the particular form of longitudinal rolls or hydrothermal waves (HTWs), as was first demonstrated in [11] and confirmed in numerous consequent studies [12–19]. HTWs are time-periodic traveling waves in the liquid, induced by instabilities of the steady Marangoni convection, which were originally predicted for the liquid layer on a rigid plate by Smith and Davis [20, 21] and later observed in [22, 23]. According to Smith and Davis [20, 21], the disturbance propagates perpendicular to the surface temperature gradient at small Prandtl numbers and almost exactly in the upstream direction at large Prandtl numbers [20, 21]. For a flat liquid layer, HTWs and BM convection usually occur under qualitatively different conditions. While the Bénard-Marangoni effect becomes more pronounced with an increase of the vertical temperature gradient in films, the appearance of HTWs is associated with a horizontal temperature gradient (for example, they can appear during lateral heating). In the case of evaporating sessile droplets, the competition between HTWs and BM convection is more complex.

The HTWs in droplets were originally identified by Sefiane et al. in 2008 [11], when the evaporation of sessile droplets of ethanol, methanol, water, and Fluorinert FC-72 was investigated. Later more detailed observations of HTWs have been reported for the ethanol droplets on four different substrates with different thermal conductivities [12]. HTWs moving in azimuthal direction have been observed for volatile droplets of ethanol and methanol. For FC-72, convective cells emerged near the droplet apex and moved towards the contact line. The number of waves has been found to increase with the increase of substrate thermal conductivity and its temperature, and to decrease with the decrease of the droplet height. On the other hand, no hydrothermal instability has been found in evaporating water droplets.

Three stages of the evaporation process with thermoconvective instabilities have been distinguished in [13] in the droplets of methanol, ethanol, and FC-72 on a polytetrafluoroethylene substrate: heating of the drop (which reaches almost the substrate temperature), evaporation with thermoconvective instabilities (the heat flux is maximal at this stage), and evaporation without thermoconvective patterns (the droplet is more like a film at this stage). The main phase is characterized by the presence of convection cells, and the origin of the cells’ movement is associated with the temperature difference between the heated substrate and the ambient temperature. Temporal evolution of the HTWs was also described by means of simultaneous thermal and fluid motion observations in a drying ethanol droplet on a heated substrate [14]. HTWs traveling in azimuthal direction in a droplet of ethanol were demonstrated to take place both under normal gravity and microgravity conditions, so that the gravity effects on the behavior of HTWs are small [15].

Sefiane et al. [16] demonstrated that HTWs in FC-72 droplets are bulk waves that extend across the entire droplet volume. Also, the influence of the HTWs on the heat transfer in the solid substrate and on evaporation rate spatial distribution was studied in [16]. A specific kind of HTWs was determined by Karapetsas et al. in [17], where three-dimensional spiral-like time-periodic traveling waves were observed that are organized radially and are uniform along the azimuthal angle. Shi et al. [24] determined critical Marangoni numbers for the emergence of the Marangoni convection instabilities in a sessile droplet with low volatility on a heated substrate by a series of three-dimensional computer simulations.

New features of the problem in question have been revealed by Semenov et al. [25], who have found that the cell patterns they determined in the droplet with a large Prandtl number represent the BM cell structure rather than HTWs. The authors have observed Marangoni instability in an ethanol droplet of capillary size on a heated and highly conductive substrate. They also performed numerical simulations by one-sided model described in [26], where they took into account, in particular, an unsteady diffusion-limited evaporation for non-isothermal pinned sessile droplet and the Stefan flow in the gas. After solving the heat transfer equation in the droplet bulk and carrying out the numerical simulation, the results obtained have agreed well with the experiment for the contact angle θ ≈ 29.3°. At the first stage, a torus roll adjacent to the contact line appeared; later it is destabilized and split into several three-dimensional unsteady BM cells occupying the whole droplet. In the third stage, the BM cells drifted towards the contact line where the Marangoni forces are stronger, and the flower pattern was observed with about 15 BM cells along the circumference, which corresponds to the spatial period about twice the local liquid thickness. The authors found that the number of BM cells increased with the decrease of the droplet height.

The interplay of the BM convection cells and HTWs has been observed in the recent work [27] in a volatile sessile droplet of silicone oil on a copper substrate at constant contact line mode over a wide range of substrate temperatures. When the substrate temperature was higher than room temperature, the BM quasistationary convection cell structure was observed and found to evolve into an oscillating state, as the evaporation progresses. When the substrate was colder than the surrounding air, the oscillating BM cells were observed only when the temperature of the substrate is higher than 10.6°C. The cell size became larger and their number was smaller when the temperature of the substrate goes up above the temperature of the surrounding gas. When the substrate temperature is above 14.3°C, the coexistence of advancing HTWs and BM vibrational convection was observed. The paper reports critical values of the contact angle at which the transition between different types of convection occurred.

In particular, the authors [27] considered the case when the substrate temperature is 7.81 K higher than the ambient temperature. Here, at the first stage, a flower structure of BM cells near the triple line emerged. With decreasing the contact angle, the cells grew in size and occupied the central region of the droplet surface (Fig. 4 in [27]).

The qualitatively similar flower structures of BM cells near the triple line at an intermediate stage of the droplet evaporation were observed in both publications [25, 27]. At the same time, the spatial structures of BM cells at sufficiently small contact angles, which were observed in [27] and numerically obtained in [25], differ substantially. The similarity of the results obtained in [25, 27] is expected as the droplet parameters considered in the two papers are close to each other. Also the relevant physical properties of 0.65 cSt silicone oil and properties of the ethanol are similar, and highly conductive heated substrates at similar temperatures are employed in both works. It is therefore surprising that the results are quite different at a later stage of the droplet evaporation. The purpose of this paper is to analyze the behavior of unsteady BM cells in volatile sessile droplets on heated substrates including the stage of comparatively small contact angles. It is also of interest to identify the main physical mechanisms, which are responsible for the behavior studied and have to be taken into account in the corresponding simulations.

We have theoretically investigated the Marangoni instability patterns in evaporating sessile droplets of ethanol and silicone oil for the particular parameters which are close to each of the experiments [25, 27]. Based on the three-dimensional numerical simulations, the fluid flows and geometric characteristics of the BM patterns in the droplet have been described. The mathematical model was developed that takes account of heat transfer in all three phases, hydrodynamics, vapor diffusion in air, Stefan flow in the gas and thermal radiation. Using ANSYS Fluent software, three-dimensional computer simulations were carried out and the unsteady temperature distributions and velocity fields in the drop were obtained. We have theoretically recovered both the flower structure of BM cells near triple line for sufficiently large contact angles and the BM cell pattern where larger BM cells occupy the fluid-gas interface for smaller contact angles.

The paper is organized as follows. Section 2 describes mathematical model and method of numerical solution. Relevance of various physical effects for the problems under consideration are also analyzed in Section 2. In Section 3 we present our main results. Section 4 contains discussion.

2. MATHEMATICAL MODEL

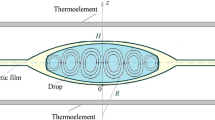
We consider three-dimensional nonstationary problem for an axially symmetrical sessile droplet on a heated solid substrate. The surface is taken as a spherical cap. This approximation is valid under the condition Bo ≪ 1, i.e., when the influence of gravitation on the droplet shape is small. Here Bo = ρgh0R/(2σ sin θ) is the Bond number, and h0 is the droplet height. We use the notations in Table 1.

Table 1. The notations and parameter values used in the calculations
Full size table

A. Diffusion of Vapor in Air

The dynamics of the vapor concentration u in the surrounding atmosphere is described by the diffusion equation

$$\frac{{\partial u}}{{\partial t}} = D\Delta u.$$
(1)

The boundary conditions are as follows: u = us on the drop surface, u = 0 far away from the drop, ∂u/∂r = 0 and ∂u/∂z = 0 on the axes r = 0 and z = 0, respectively.

Semenov et al. derive in [26] and employ in [25] analytical equations for the unsteady diffusion-limited evaporation from sessile droplets, which agree with the numerical results of [28]. However, these unsteady effects are small on time scales larger than the time required for the Brownian particle to pass the characteristic length R. i.e., for t \( \gtrsim \) R2/D ~ 0.7 s, for the problems under consideration. Therefore, the evaporation kinetics can be considered as a steady state process and one can use the quasi-stationary approximation

$$\Delta u = 0$$
(2)

with the same boundary conditions together with the spherical cap approximation.

The latter problem is mathematically equivalent to the one for the electrostatic potential of a charged conductor with a shape formed by two intersecting spheres. Such a problem has been solved analytically in [29] in terms of toroidal coordinates. Based on this circumstance, the analytic solution for Eq. (2) with the above boundary conditions, that describes the inhomogeneous evaporation flux density J(r) from the surface of the evaporating droplet, was presented in [30] in the form

$$\begin{gathered} J(r) = {\text{|}}D\nabla u{\text{|}} = \frac{{D{{u}_{s}}}}{R}\left( {\frac{{\sin \theta }}{2} + \sqrt 2 {{{(x(r) + \cos \theta )}}^{{3/2}}}_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}}} \right. \\ \,\left. { \times \int\limits_0^\infty {\frac{{\cosh (\theta \tau )}}{{\cosh (\pi \tau )}}\tau \tanh ((\pi - \theta )\tau ){{P}_{{ - 1/2 + i\tau }}}(x(r))d\tau } } \right), \\ \end{gathered} $$
(3)

where

$$\begin{gathered} x(r) = ({{r}^{2}}\cos \theta {\text{/}}{{R}^{2}} \\ \, + \sqrt {1 - {{r}^{2}}{{{\sin }}^{2}}\theta {\text{/}}{{R}^{2}}} ){\text{/}}(1 - {{r}^{2}}{\text{/}}{{R}^{2}}) \\ \end{gathered} $$
(4)

and P–1/2 + iτ(x) is the Legendre polynomial. Expression (3) can be conveniently approximated as [30, 31]

$$J(r) = {{J}_{0}}(\theta ){{\left( {1 - \frac{{{{r}^{2}}}}{{{{R}^{2}}}}} \right)}^{{ - \lambda (\theta )}}},$$
(5)

where λ(θ) = 1/2 – θ/π. The coefficient J0(θ) in (5) can be fitted as follows:

$$\frac{{{{J}_{0}}(\theta )}}{{1 - \Lambda (\theta )}} = {{J}_{0}}(\pi {\text{/}}2)(0.27{{\theta }^{2}} + 1.3),$$
(6)
$$\Lambda (\theta ) = 0.22{{(\theta - \pi {\text{/}}4)}^{2}} + 0.36,$$
(7)
$${{J}_{0}}(\pi {\text{/}}2) = \frac{{D{{u}_{s}}}}{R},$$
(8)

where us is the saturated vapor density at the droplet free surface. It is numerically obtained in [31] that Eqs. (5)–(8) represent an accurate fit for the solution of Eq. (2) with the above boundary conditions, within the spherical cap approximation. The fit is valid in a wide range of contact angles, and its accuracy does not depend on the parameters such as D and R. For this reason, we employ the Eqs. (5)–(8) in the simulations.

Saturated vapor pressure is determined by the Antoine equation (with ps in (Pa) and T in (K)):

$${{\log }_{{10}}}{{p}_{s}}(T) = A - \frac{B}{{C + T}},$$
(9)

where A, B, and C are empirical constants. We use A = 10.247, B = 1599.039, C = –46.391 for ethanol [32]. For 0.65 cSt silicone oil, we use A = 9.418, B = 1509, C = –31.55 [18].

The concentration of vapor us at the drop surface is calculated from ideal gas law and defined by

$${{u}_{s}}(T) = \frac{{M{{p}_{s}}(T)}}{{\bar {R}T}},$$
(10)

where \(\bar {R}\) is the universal gas constant, and M is molar mass of the vapor.

It follows from (5) that the mass loss resulting from vaporization occurs nonuniformly along the free surface of the liquid layer, significantly increasing near the pinned contact line. A nonuniform mass flow during evaporation and the corresponding heat transfer change the temperature distribution along the droplet surface and cause Marangoni forces due to temperature-dependent surface tension. These forces produce thermocapillary convection inside a droplet.

B. Stefan Flow in the Gas

Because the saturated vapor concentration is not much smaller than the density of air (see Table 1), it is natural to consider the contribution of the Stefan flow in the gas for the problems under consideration [33].

As a result of the convective mass transport in the gas, the evaporation rate increases as [26]:

$$\tilde {J}(r) = \frac{{{{u}_{g}}}}{{{{u}_{s}}}}\ln \left( {\frac{{{{u}_{g}}}}{{{{u}_{g}} - {{u}_{s}}}}} \right)J(r),$$
(11)

where ug = Mgpg/(\(\bar {R}\)T), pg is the air pressure, Mg = Mair(1 – \({{X}_{{v}}}\)) + \({{M}_{{v}}}{{X}_{{v}}}\) is the molar mass of gas near droplet free surface, Mair and \({{M}_{{v}}}\) are molar masses of corresponding air and vapor, \({{X}_{{v}}}\) = us\(\bar {R}\)T/(\({{M}_{{v}}}\)pg) is the vapor molar fraction. Here, the surface temperature T is a function of r.

It follows that the Stefan flow in the gas increases the evaporation rate by approximately 10 and 18% for droplets of ethanol and 0.65 cSt silicone oil, respectively.

The results below in Section 3 do not account for the Stefan flow in the gas. However, our preliminary numerical calculations for the 0.65 cSt silicone oil droplet with parameters specified in Table 1 and contact angle 20.49° show that the influence of the Stefan flow on the resulting surface temperature distribution is quite small.

C. Hydrodynamics

The governing equations for the fluid dynamics inside the drop are the Navier-Stokes equations and the continuity equation for the incompressible fluid

$$\frac{{\partial {\mathbf{v}}}}{{\partial t}} + ({\mathbf{v}} \cdot \nabla ){\mathbf{v}} + \frac{1}{\rho }{\text{grad}}{\kern 1pt} p = \nu \Delta {\mathbf{v}},$$
(12)
$${\text{div}}{\kern 1pt} {\mathbf{v}} = 0.$$
(13)

Here ν = η/ρ is kinematic viscosity, v is fluid velocity, p is pressure.

The boundary conditions for the Eqs. (12), (13) include the no-slip condition v = 0 at the substrate-fluid interface and the condition at fluid-gas interface which involves the Maranogoni forces associated with the temperature dependence of the surface tension. In general, the latter boundary condition can be expressed as [34]

$$\begin{gathered} \left( {p - {{p}_{{v}}} - \sigma \left( {\frac{1}{{{{R}_{1}}}} + \frac{1}{{{{R}_{2}}}}} \right)} \right){{n}_{i}} \\ = \eta \left( {\frac{{\partial {{{v}}_{i}}}}{{\partial {{x}_{k}}}} + \frac{{\partial {{{v}}_{k}}}}{{\partial {{x}_{i}}}}} \right){{n}_{k}} - \frac{{\partial \sigma }}{{\partial {{x}_{i}}}}, \\ \end{gathered} $$
(14)

where the unit vector n is directed towards the vapor along the normal to the surface. Taking the tangential component of this equation, one finds

$$\frac{{d\sigma }}{{d\tau }} = \eta \left( {\frac{{\partial {{{v}}_{\tau }}}}{{\partial n}} + \frac{{\partial {{{v}}_{n}}}}{{\partial \tau }} - {{{v}}_{\tau }}\frac{{d\varphi }}{{d\tau }}} \right).$$
(15)

Here dσ/dτ = σT ⋅ dT/dτ, τi are the components of the unit vector τ tangential to the surface, and φ is the angle between the normal vector to the drop surface and the vertical axis. We note that the ANSYS Fluent simulation package allows assigning directly the Marangoni stress at the droplet free surface, so Eq. (15) is already implemented in the software and a user does not need to employ it.

D. Heat Transfer in the Drop

The temperature distribution is obtained with the heat conduction equation

$$\frac{{\partial T}}{{\partial t}} + {\mathbf{v}} \cdot \nabla T = \kappa \Delta T.$$
(16)

The heat conduction inside the substrate is obtained with

$$\frac{{\partial T}}{{\partial t}} = \kappa \Delta T.$$
(17)

The boundary conditions for the thermal conduction include the isothermal boundary condition at the lower bound of substrate T = Ts, the adiabatic boundary condition at the substrate-gas interface ∂Ts/∂n = 0, and the continuity of the heat flux at the substrate-fluid interface ks∂Ts/∂z = k∂TL/∂z. Here TL and Ts correspond to the liquid and substrate temperature, k and ks are thermal conductivities of liquid and substrate, respectively.

Following the experiments [25, 27], the calculations in the present work involve a highly conducting substrate. In this case, the boundary conditions can be written simply as T = Ts at the substrate-fluid interface.

The boundary condition for the heat transfer at the droplet surface is

$$\frac{{\partial T}}{{\partial n}} = - \frac{{{{Q}_{0}}(r)}}{k}.$$
(18)

Here,

$${{Q}_{0}}(r) = - {{k}_{{{\text{air}}}}}{{\left( {\frac{{\partial T}}{{\partial n}}} \right)}_{{{\text{air}}}}} + L\tilde {J}(r) + {{\dot {q}}_{r}}$$
(19)

is the total heat flux from the droplet surface, which includes latent heat of evaporation, effects of the thermal conduction in liquid and gas and thermal radiation. The estimates below show that all these effects are important for droplets evaporating from heated substrates. Also, n is a normal vector to the droplet upper surface, kair(∂T/∂n)air is the heat flow associated with non-uniform temperature distribution in an ambient gas, kair is the thermal conductivity of air, J(r) is the local evaporation rate determined by (5),

$${{\dot {q}}_{r}} = {{\sigma }_{B}}\varepsilon ({{T}^{4}} - T_{a}^{4})$$
(20)

is the net radiation flux between the drop and the environment; here σB is the Stefan-Boltzman constant, ε is the emissivity; T and Ta are the droplet surface temperature and temperature of the ambient gas, respectively.

The relation (20) can be employed under the following condition. First, it is important that the droplet size is much larger than the characteristic wavelengths of the thermal radiation, which are determined by the Planck distribution. Under this condition the emissivity almost does not depend on the frequency [35]. And vise versa, for objects with dimensions much smaller than the thermal wavelength, super-Planckian far-field radiative heat transfer is possible [36, 37]. Secondly, it is important that the temperature difference inside the drop is much smaller than the temperature difference between the droplet and the ambient gas.

Let’s obtain the relation for (∂T/∂n)air .

The quasi-stationary temperature distribution in the gas phase is determined by the equation

$$\Delta T = 0$$
(21)

with the boundary conditions: T = Ts at the droplet surface (under the assumption that the temperature difference inside the drop is much smaller than the temperature difference between the droplet and the ambient gas), T = Ta away from the droplet. This problem is mathematically equivalent to Eq. (2) with the corresponding boundary conditions, therefore, one can employ the same formulas for the analytical solution. It follows from (5)–(8) that the quantity J(r)/(Dus) depends only on the geometry of the problem. It follows from the mathematical equivalence that

$$\frac{{J(r)}}{{D{{u}_{s}}}} = \frac{1}{{{{T}_{s}} - {{T}_{a}}}}{{\left( {\frac{{\partial T}}{{\partial n}}} \right)}_{{{\text{air}}}}}.$$
(22)

Therefore, the main boundary condition at the droplet surface takes the form (19), where (∂T/∂n)air is calculated similarly to Eqs. (5)–(8):

$${{\left( {\frac{{\partial T}}{{\partial n}}} \right)}_{{{\text{air}}}}} = {{J}_{1}}(\theta ){{\left( {1 - \frac{{{{r}^{2}}}}{{{{R}^{2}}}}} \right)}^{{ - \lambda (\theta )}}},$$
(23)
$$\frac{{{{J}_{1}}(\theta )}}{{1 - \Lambda (\theta )}} = {{J}_{1}}(\pi {\text{/}}2)(0.27{{\theta }^{2}} + 1.3),$$
(24)
$${{J}_{1}}(\pi {\text{/}}2) = \frac{{T - {{T}_{a}}}}{R}.$$
(25)

E. Heat Transfer in the Gas Phase

Here, we estimate the relative strength of the heat fluxes LJ(r) and kair (∂T/∂n)air, which are summands in (19). If follows from (22) that the heat fluxes are equal when

$${{T}_{s}} - {{T}_{a}} = \frac{{LD{{u}_{s}}}}{{{{k}_{{{\text{air}}}}}}}.$$
(26)

Hence, the contribution of the effect of heat conduction in air matches the evaporation cooling heat flux for

$${{T}_{s}} - {{T}_{a}} \approx \left\{ \begin{gathered} 60.91K\quad {\text{for}}\,\,{\text{ethanol}}, \hfill \\ 0.94K\quad {\text{for}}\,\,{\text{hexanol}}{\text{,}} \hfill \\ 22.53K\quad {\text{for}}\,\,{\text{silicone}}\,\,{\text{oil}}{\text{.}} \hfill \\ \end{gathered} \right.$$
(27)

The present work considers the case Ts – Ta ~ 10 K for droplets of ethanol and silicone oil, so taking into account the effect of heat transfer in the gas phase is worthwhile for obtaining quantitative results.

F. Thermal Radiation

Here, we estimate the relative strength of the evaporative cooling heat flux LJ(r) and the thermal radiation heat flux (20) between the droplet and the environment.

It follows from Eqs. (5)–(8) that the heat fluxes are roughly equal for

$$T\sim {{\left( {\frac{{LD{{u}_{s}}}}{{{{\sigma }_{B}}\varepsilon R}} + T_{a}^{4}} \right)}^{{1/4}}}.$$
(28)

Hence, the contribution of the effect of thermal radiation matches the evaporative cooling heat flux for

$${{T}_{s}} - {{T}_{a}} \approx \left\{ \begin{gathered} 70.6K\quad {\text{for}}\,\,{\text{ethanol}}, \hfill \\ 1.61K\quad {\text{for}}\,\,{\text{hexanol}}{\text{,}} \hfill \\ 30.69K\quad {\text{for}}\,\,{\text{silicone}}\,\,{\text{oil}}{\text{.}} \hfill \\ \end{gathered} \right.$$
(29)

The present work considers the case Ts – Ta ~ 10 K for droplets of ethanol and silicone oil, so taking into account the effect of thermal radiation is worthwhile for obtaining quantitative results.

G. Numerical Simulation

We solve the thermal conduction equation and the Navier-Stokes equations by the finite element method using computational fluid dynamics simulation package ANSYS Fluent. The simulation includes several steps.

• Geometry and mesh generation

We create three-dimensional geometry of the axially symmetrical droplet. The surface curvature radius and the droplet height are equal to R/sin θ and R(1/sin θ – cot θ), respectively. The next step is to divide the simulation region into small computational cells. The number of cells is between 200 and 500 thousand depending on contact angle.

• Defining model and setting properties

We choose the pressure-based solver type, transient mode for time, viscous (laminar) flow and enable the calculation of energy in the model. We specify all physical properties of the fluid such as density, viscosity, the temperature derivative of the surface tension σT, which allows us to specify the properties of Marangoni stress, etc.

• Setting boundary conditions and solution method

The boundary conditions are set according to Section 2. The rate of heat loss (19) is specified with a user-defined function (UDF) written in the C programming language. The solution algorithm is SIMPLE (Semi-Implicit Method for Pressure Linked Equations) [38]. The main feature of this method is using a relationship between velocity and pressure corrections to enforce mass conservation and to obtain the pressure field. The algorithm is written in such a way that the continuity equation is automatically satisfied.

• Post-processing

We display the simulation results: velocity field, absolute values of velocity, and temperature distribution and then analyze the vortex structure and wave patterns.

3. RESULTS AND DISCUSSION

Figure 1 shows experimental results from Fig. 4 in [27] and our numerical results for the drying droplet of 0.65 cSt silicone oil. Here Ts = 302.69 K, Ta = 294.88 K, R = 2.09 mm, and the droplet contact angle is 28.39°, 20.49°, and 17.18°. The diffusion of vapor in air, the hydrodynamics in the drop, effects of the thermal conduction in all three phases and thermal radiation have been taken into account as discussed above in Section 2.

Fig. 1.
figure 1

Evolution of surface temperature patterns of the silicone oil droplet. Left panel shows experimental data and is reprinted from [27] (Copyright (2019), with permission from Elsevier). Right panel shows the corresponding surface temperature patterns obtained by means of computer simulation using the parameters from Table 1.

Full size image

The obtained behavior of the BM cells qualitatively agrees with the experimental data: there is a flower pattern for large contact angle, while the BM cells occupy the whole droplet surface for small contact angles. The simulation did not take into account the temporal dynamics of the droplet profile, and so the quantitative details such as the particular number of BM cells can vary.

We note that the Prandtl number is quite large for the problems under consideration, so the HTW instability mechanism [20, 21] tends to move the BM cells from the droplet apex towards the contact line.

Figure 2 shows that the oscillation of the pattern is very slow compared to the characteristic frequences of HTWs in [11, 12]. Therefore, we confirm the existence of irregular oscillatory BM convection rather than HTWs in this case. The Marangoni convection cells are sufficiently deep and are extended in the droplet bulk, as seen in Fig. 3.

Fig. 2.
figure 2

Temporal dependence of the BM instabilities obtained for the silicone oil droplet for θ = 20.49°. The graphs correspond to the following values of the evaporation time: (a) 8, (b) 18, (c) 28, (d) 38, (e) 48, (f) 58, (g) 68 s, respectively. Temporal evolution of the droplet profile is not taken into account, so the contact angle is fixed during the simulation.

Full size image
Fig. 3.
figure 3

Side view from the simulations of the silicone oil droplet with θ = 20.49°.

Full size image

Figure 4 was obtained for the drying droplet of ethanol. Here, Ts = 307.05 K, Ta = 297.55 K, R = 2.95 mm, θ = 29.2°. The temporal dynamics of the droplet profile has not been taken into account. The numerical results qualitatively agree with the experimental data. We obtained 20 BM cells, similarly to the numerical results of [25] which were obtained by much different method. We confirm the result of [25] that the obtained instability can be described as unsteady BM convection rather than HTWs.

We did not calculate the IR image with Eq. (31) from [25] because we believe that equation is incorrect. In particular, the equation is written under the assumption that the thermal radiation propagates only in the upright direction. Also, the equation employs the Stefan-Bolzmann equation and does not take into account that the maximum of Planck distribution is outside of the mid-wavelength range visible by the IR camera, i.e., the IR camera passes by major part of the radiation.

Fig. 4.
figure 4

Surface temperature patterns and the velocity vector field plot for the ethanol droplet with θ = 29.2°. (a) Experimental data, reprinted with permission from [25] (2017 © AIP Publishing). (b) The corresponding surface temperature pattern obtained by means of computer simulation using the parameters from Table 1. (c) The vector field plot of numerically obtained surface velocity.

Full size image

Figure 5 shows the obtained temperature distribution at the droplet surface for θ = 29.2°, 24°, 20°, and 15°. There is a flower pattern for large contact angle, while the BM cells occupy the whole droplet surface for sufficiently small contact angles. This behavior is different from the one obtained numerically in [25], where the BM cells were located only in the vicinity of the contact line, and the number of such BM cells increased with the decrease of the droplet height. However, the behavior is similar to Fig. 1, which is natural because the relevant physical parameters are quite close.

Fig. 5.
figure 5

Thermal patterns obtained by computer simulation of the ethanol droplet for θ = (a) 29.2°, (b) 24°, (c) 20°, and (d) 15°.

Full size image

4. CONCLUSION

We have carried out three-dimensional computer simulations of unsteady Marangoni instabilities in drying sessile droplets of ethanol and silicone oil of capillary size on a heated highly conductive substrate. We have analyzed the relevance of physical effects in this case and found that in addition to the nonstationary three-dimensional thermal conduction in the droplet, nonstationary three-dimensional dynamics of incompressible fluid and diffusion of vapor in air, heat exchange in the vapor phase and radiation flux between the drop and the environment also need to be taken into account. However, contributions of such effects as nonstationary effects in the diffusion of vapor in air are insignificant. Interestingly, we have found that the well-known analytical solution for the diffusion-limited evaporation rate [30], that significantly simplifies the calculation of the heat transfer in the droplet, can also be employed for calculation of thermal conduction in the gas phase.

Our results agree well with the experimental results of [25, 27]. We confirm the conclusion of these works that the instability in this case is a nonstationary BM convection rather than HTWs.

We also clarify the behavior of the BM instabilities with decrease of the contact angle. We find that a decrease of the contact angle results in increasing BM cells, eventually transforming the flower pattern into the spatial structure, where the BM cells occupy the whole droplet. Such a behavior has been observed experimentally in [27] but has not been obtained numerically until now, to the best of our knowledge. We find that this behavior applies to the drying ethanol droplet of [25] as well. This resolves the discrepancy between the BM cell behavior in [27] and in [25].

Our results are also consistent with the recent experimental results of [39], which show that the HTWs in the droplet appear only for relatively large contact angles.

We believe that our results represent a useful step towards a better understanding of the thermocapillary instabilities in evaporating droplets.