Finite-element method based solver for an evaporating sessile droplet on a heated surface

Abstract

We report the development of a finite-element-based solver to compute transport of mass, momentum and energy during evaporation of a sessile droplet on a heated surface. The evaporation is assumed to be quasi-steady and diffusion-limited. The heat transfer between the droplet and substrate and mass transfer of liquid-vapor are solved using a two-way coupling. In particular, here, we develop and implement the formulation of fluid flow inside the droplet in the model. The continuity and Navier–Stokes equations are solved in axisymmetric, cylindrical coordinates. Jump velocity boundary condition is applied on the liquid–gas interface using the evaporation mass flux. The governing equations are discretized in the framework of the Galerkin weight residual approach. A mesh of finite triangular elements with six nodes is utilized, and quadratic shape functions are used to obtain the second-order accurate numerical solution. Two formulations, namely, penalty function and velocity pressure, are employed to obtain discretized equations. The numerical results are the same using both methods, and the latter is around 30–50% faster than the former for the cases of refined grid. Computed flow fields are in excellent agreement with published results. The solver’s capability is demonstrated by solving the internal flow field for a case of a heated substrate.

1 Introduction

Understanding the evaporation of a sessile droplet on a solid surface has been a much-studied problem in the last two decades [1]. It is central to several technical applications such as ink-jet printing, spray cooling, and bioassays. Recently, sessile droplet evaporation has been studied in the context of fomite transmission of COVID-19 [2,3,4]. The flow field inside the droplet is essential for designing the above-mentioned technical applications. In particular, self-assembly of colloidal particles is dictated by the internal flow during the evaporation [5,6,7,8,9]. The computational modeling of the internal fluid flow is challenging since fluid flow inside the droplet, heat transfer between the droplet and substrate, and mass transfer of liquid vapor from the droplet are coupled. The evaporation mass flux on the liquid–gas interface is non-uniform, and it influences the temperature and flow field inside the droplet.

Previous numerical studies reported evaporation dynamics of a sessile droplet on a non-heated substrate. These reports made certain assumptions for the sake of computational tractability. Girard et al [10] investigated Marangoni convection inside the evaporating droplet using a commercial finite-element solver while neglecting the pressure gradient terms in the Naiver-Stokes equations. Widjaja et al [11] tested two meshing techniques, namely, spine and elliptic, in their FE model and reported that elliptic mesh provides more accurate results and resolves flow near the contact line. Barash et al [12] developed a finite-difference model to investigate evaporation of droplets and flow inside them. They compared their simulation results with experimental measurements for evaporation of toluene droplets. They reported different stages of vortices formation inside the droplet as it evaporates.

Bourantas et al [13] solved fluid flow inside the evaporating droplet using the velocity-correction method with meshless point collocation. They reported better accuracy and convergence rate compared to traditional mesh-based models. Using commercial FE solver, Barmi and Meinhart [14] simulated the convective flow inside the pinned evaporating droplet while assuming axisymmetric flow field, temperature, and vapor concentration distribution. They concluded that flow inside the droplet is responsible for particle deposition patterns, but it does not influence heat transfer much, and conduction remains the primary mode of heat transfer. Barash [15] investigated the dependence of vortex structures in the droplet on substrate properties using a transient Navier–Stokes solver. The transient model solves the evaporation profile while neglecting the contribution of convection inside the droplet and uses it to calculate boundary conditions at the liquid–gas interface.

Al-Sharfi et al [16] used a finite element method-based software on studying flow and heat transfer characteristics inside evaporating droplets resting on hydrophilic and hydrophobic substrates. They reported strong dependence of the heat transfer rate on the droplet contact angle. Pradhan and Panigrahi [17] investigated flow inside sessile and pendant droplets of aqueous salt solution using commercial software. They showed that the orientation of the droplet strongly influences the convection inside it. Bouchenna et al [18] developed a finite volume model to study the effect of substrate heating on flow pattern inside the droplet with quasi-steady evaporation while accounting for thermal buoyancy and thermocapillary effect on the flow. Chen et al [19] reported the effect of substrate thermal properties on the bulk fluid flow inside the droplet, using a commercial finite element solver.

A brief literature survey shows that previously-reported computational methods developed in this context focused on the non-heated substrate. To the authors’ knowledge, no studies have reported high-fidelity modeling of the sessile droplet evaporation on a heated surface thus far. To this end, we report a finite-element method based solver to compute diffusion-limited and quasi-steady droplet evaporation on a heated surface. In our previous work [20], we reported a finite-element method-based solver for calculating heat transfer between the droplet and substrate, and mass transfer of liquid-vapor, using a two-way coupling. In the present work, we extend this solver to account for fluid flow inside the droplet. Here we benchmark and validate the solver with previous studies and demonstrate the second-order accuracy of the solver. Lastly, the solver has been demonstrated to compute the flow field inside the evaporating droplet on a heated surface.

2 Computational model

2.1 Assumptions and limitations of the model

We present the computational model for quasi-steady, diffusion-limited evaporation of a sessile droplet, with a pinned contact line during the evaporation. The flow, thermal and concentration of liquid vapor fields are to be considered as axisymmetric. The assumptions in the model, justified in previous works [21,22,23,24] are briefly described as follows. The evaporation occurs by diffusion of liquid-vapor in quiescent air. The droplet’s wetted diameter is lesser than the capillary length such that the droplet assumes a spherical cap during the evaporation. For the evaporation of microliter droplets, the internal flow is on the order of $\upmu \hbox{m}$/s, and therefore, inertial terms in Navier–Stokes equation are neglected, due to small Reynolds number (O(10$^{-3}$)). The Reynolds number is based on the evaporation-induced velocity inside the droplet and wetted radius of the droplet. In the context of heat transfer, convection inside and outside of the droplet, and radiative heat transfer from the liquid–gas interface are neglected.

2.2 Heat and mass transfer

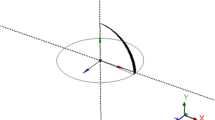
Using a two-way coupling, reported in our earlier work [20], we solved temperature field in the droplet and substrate, and concentration of liquid vapor outside the droplet in asymmetric cylindrical coordinates (figure 1). The details of the model and numerical methodology are given in Ref. [20] and here we briefly describe governing equations and boundary conditions used in this model. In the framework described in section 2.1, the energy equations for droplet and substrate are given by,

$$\begin{aligned} \nabla ^2T_i=0 \end{aligned}$$

(1)

where T is temperature and, $i=1$ and 2 correspond to the droplet and substrate, respectively.

Figure 1

Computational domain and boundary conditions used in the present computational model.

The following heat transfer boundary conditions are applied. The substrate bottom surface is prescribed with a given temperature. The side and top surface of the substrate are insulated. A perfect thermal contact is considered at liquid–solid interface. At liquid–gas interface, the following jump energy condition is enforced [25]:

$$\begin{aligned} j L = -k \nabla T|_{LG} \cdot {{\textbf {n}}} \end{aligned}$$

(2)

where j is the evaporative flux [kg m$^{-2}$ s$^{-1}$] at the liquid–gas interface, L is the latent heat of the evaporation [J kg$^{-1}$], k is thermal conductivity of the droplet [W m$^{-1}$ K$^{-1}$], LG denotes liquid–gas interface and n is unit normal vector on the liquid–gas interface.

The concentration, c [kg m$^{-3}$] of liquid vapor outside droplet in ambient is governed by the following equation,

$$\begin{aligned} \nabla ^2c=0 \end{aligned}$$

(3)

The boundary conditions for mass transport of liquid vapor are described as follows. The value of c on the far-field boundaries is taken as $Hc_{sat, \infty }$, where $c_{sat, \infty }$ is the saturated concentration (kg m$^{-3}$) of the water vapor in the far-field and H is relative humidity. The concentration at the liquid–gas interface is prescribed at its saturated value at the interface temperature. The evaporative mass flux j at the liquid–gas interface is expressed in terms of c as follows [7, 21, 23],

$$\begin{aligned} j(r, T) = D(T) \nabla c|_{LG} \cdot {{\textbf {n}}} \end{aligned}$$

(4)

where r is radial coordinate and D(T) is diffusion coefficient of liquid vapor in air as a function of temperature [7].

Eqs. 1–4 are solved using finite-element method using two-way coupling, as described in our previous work [20]. The thermal and concentration field are obtained after a successful convergence of the coupling. Using computed j, evaporation rate ${\dot{m}}$ is computed by integrating j over area of liquid–gas interface by the following expression:

$$\begin{aligned} {\dot{m}} = \rho \frac{\partial V}{\partial t} = \int _A 2\pi r j ds \end{aligned}$$

(5)

where $\rho$ is droplet density, V is instantaneous droplet volume and A is area of liquid–gas interface. j and ${\dot{m}}$ are used while applying boundary conditions of flow solver, as described in next section. The modules of the solver are schematically shown in figure 2.

Figure 2

Different modules of the solver and data exchange between them.

2.3 Fluid flow in the droplet

In the framework described in section 2.1, the governing equation of the fluid flow inside the droplet are continuity and Navier–Stokes equations. The equations are written in axisymmetric cylindrical coordinates (r, z) as follows:

$$\begin{aligned}{} & {} \frac{1}{r} \frac{\partial (ru)}{\partial r} + \frac{\partial v}{\partial z} = 0 \end{aligned}$$

(6)

$$\begin{aligned}{} & {} \frac{1}{r} \frac{\partial (r\sigma _{rr})}{\partial r} + \frac{\partial \sigma _{rz}}{\partial z} - \frac{\sigma _{\theta \theta }}{r}= 0 \end{aligned}$$

(7)

$$\begin{aligned}{} & {} \frac{1}{r} \frac{\partial (r\sigma _{zr})}{\partial r} + \frac{\partial \sigma _{zz}}{\partial z} = 0 \end{aligned}$$

(8)

where the components of the stress tensor are defined as follows:

$$\begin{aligned}{} & {} \sigma _{rr} = 2\mu \frac{\partial u}{\partial r} - P \end{aligned}$$

(9)

$$\begin{aligned}{} & {} \sigma _{zz} = 2\mu \frac{\partial v}{\partial z} - P \end{aligned}$$

(10)

$$\begin{aligned}{} & {} \sigma _{\theta \theta } = 2\mu \frac{u}{r} - P \end{aligned}$$

(11)

$$\begin{aligned}{} & {} \sigma _{rz} = \sigma _{zr} = \mu \left( \frac{\partial v}{\partial r} + \frac{\partial u}{\partial z} \right) \end{aligned}$$

(12)

The boundary conditions for the fluid flow (figure 1) are expressed as follows: At liquid–solid interface ($z = 0$, $r \le R$), no slip boundary condition ($u = 0, v = 0$) is applied. At $r = 0$, axisymmetric boundary condition is applied: $u = 0$ and $\partial v$ / $\partial r = 0$. At liquid–gas interface, two boundary conditions are applied: (a) zero shear stress boundary condition in tangential direction to the interface ($\tau _t = 0$) (b) Jump velocity or kinematic boundary condition, given by [26],

$$\begin{aligned} u_n = \frac{j}{\rho }-n_z\frac{\partial h}{\partial t} \end{aligned}$$

(13)

where $u_n$ is fluid velocity at liquid–gas interface, normal to the interface, $\partial h/ \partial t$ is the velocity of the interface in axial direction and $n_z$ is component of unit normal vector n in axial direction. The radial and axial components ($n_r$ and $n_z$) of the normal vector are defined as follows [26],

$$\begin{aligned} n_{r}&= \frac{r\sin \theta }{R} \\ n_{z}&= \sqrt{1-(n_r)^2} \end{aligned} $$

(14)

where $\theta$ and R are contact angle and wetted radius, respectively. The volume of the spherical cap droplet as a function of droplet height H is given by,

$$\begin{aligned} V = \frac{\pi h}{6}(3R^2+H^2) \end{aligned}$$

(15)

We consider a pinned contact line or constant contact radius (CCR) mode of evaporation. The velocity at the top ($r=0$) of the droplet (dH/dt) is obtained by differentiating eq. 15 with respect to t, keeping R as constant [14]. After differentiation and using eq. 5, we obtain dH/dt as follows,

$$\begin{aligned} \frac{dH}{dt} = \frac{2{\dot{m}}}{\rho \pi (R^2+H^2)} \end{aligned}$$

(16)

The height of liquid–gas interface h(r, t) is defined as follows [21],

$$\begin{aligned} h(r,t) = \sqrt{\left( \frac{R^2}{\sin ^2\theta } - r^2\right) } - \frac{R}{\tan \theta } \end{aligned}$$

(17)

Differentiating eq. 17 and using definition of contact angle, $\tan (\theta /2)=H/R$, we obtain expression of $\partial h/ \partial t$ as follows [26]:

$$\begin{aligned} \frac{\partial h }{\partial t }= \frac{dH}{dt} \left[ \frac{H^4-R^4}{4H^3\sqrt{\left( \frac{H^2+R^2}{2H}\right) ^2-r^2}} + \frac{R^2+H^2}{2H^2}\right] \end{aligned}$$

(18)

In case of constant contact angle (CCA) mode of evaporation, V in eq. 15 is expressed in terms of $\theta$ and H and eq. 15 is differentiated, keeping $\theta$ as constant. In case of a mixed mode of evaporation, say CCR mode followed by CCA mode, formulations of both CCA and CCR can be combined together. In this case, receding contact angle $\theta _{rec}$, the contact angle at which contact line recedes, may be available from companion experiment.

2.4 FEM formulation

We implement Galerkin weighted residual approach, in which, weight function ($w_i$) are the same as shape function or approximation function [27]. Using weight function, the following weak form of Navier–Stokes equation was obtained to lower the requirement of choosing higher-order approximation function [27]:

$$\begin{aligned}{} & {} \int _{\Omega _e} w_i \left[ \frac{1}{r} \frac{\partial (r\sigma _{rr})}{\partial r} + \frac{\partial \sigma _{rz}}{\partial z} - \frac{\sigma _{\theta \theta }}{r} \right] d\Omega = 0 \end{aligned}$$

(19)

$$\begin{aligned}{} & {} \int _{\Omega _e} w_i \left[ \frac{1}{r} \frac{\partial (r\sigma _{zr})}{\partial r} + \frac{\partial \sigma _{zz}}{\partial z} \right] d\Omega = 0 \end{aligned}$$

(20)

where $d\Omega = 2\pi r dr dz$ is differential volume in axisymmetric cylindrical coordinates and $\Omega _e$ represents a finite-element. After solving and rearranging differential terms in integrals in Eqs. 19–20, we get the following equations:

$$\begin{aligned}{} & {} \int _{\Omega _e} \left[ \frac{\partial w_i (\sigma _{rr})}{\partial r} + \frac{\partial w_i \sigma _{rz}}{\partial z} + \frac{w_i \sigma _{\theta \theta }}{r} \right] rdrdz \\{} & {} \quad = \int _{\Gamma _e} w_i (t_r)rds \end{aligned}$$

(21)

$$\begin{aligned}{} & {} \int _{\Omega _e} \left[ \frac{\partial w_i (\sigma _{zr})}{\partial r} + \frac{\partial w_i \sigma _{zz}}{\partial z} \right] rdrdz= \int _{\Gamma _e} w_i (t_z)rds \end{aligned}$$

(22)

where $t_r = \sigma _{rr}n_r+\sigma _{rz}n_z$ and $t_z = \sigma _{zr}n_r+\sigma _{zz}n_z$ are the boundary stress components in radial and axial directions, respectively. $\Gamma _e$ represents the boundary of the element and differential surface area ($d\Gamma$) of the axisymmetric geometry is $2\pi rds$, where ds is differential arc length of the boundary or liquid–gas interface.

2.4.1 Penalty function formulation

In penalty function formulation, pressure (P) is eliminated from Navier–Stokes equations [27]. The elimination of pressure leads to a constrained problem and where constrained equation is the continuity equation (eq. 6). The constrained problem is reformulated as an unconstrained problem and pressure P is replaced by following function [27]:

$$\begin{aligned} P = -\gamma \left( \frac{\partial u}{\partial r} + \frac{\partial v}{\partial z} + \frac{u}{r} \right) \end{aligned}$$

(23)

where $\gamma$ is a penalty factor which should be a large arbitrary value [27], i.e. $\mu \times 10^{10}$. After calculating velocities, pressure (P) is recovered using eq. 23. Substituting $\sigma _{rr}$, $\sigma _{zz}$, $\sigma _{\theta \theta }$, $\sigma _{rz}$ and P from eq. 9, 10, 11, 12 and 23, respectively, in eqs. 21 and 22, the following equations are obtained:

$$\begin{aligned}{} & {} \int _{\Omega _e} \left[ 2\mu \frac{\partial w_i}{\partial r} \frac{\partial u}{\partial r} + \mu \frac{\partial w_i}{\partial z} \left( \frac{\partial u}{\partial z} + \frac{\partial v}{\partial r} \right) + 2\mu \frac{w_i}{r} \frac{u}{r} \right. \\{} & {} \quad \left. + \gamma \frac{\partial w_i}{\partial r} \left( \frac{\partial u}{\partial r} + \frac{\partial v}{\partial z} + \frac{u}{r} \right) \right. \\{} & {} \quad \left. + \gamma \frac{w_i}{r} \left( \frac{\partial u}{\partial r} + \frac{\partial v}{\partial z} + \frac{u}{r} \right) \right] rdrdz= \int _{\Gamma _e} w_i (t_r)rds \end{aligned}$$

(24)

$$\begin{aligned}{} & {} \int _{\Omega _e} \left[ \mu \frac{\partial w_i}{\partial r} \frac{\partial u}{\partial z} + \mu \frac{\partial w_i}{\partial r} \frac{\partial v}{\partial r} + 2\mu \frac{\partial w_i}{\partial z} \frac{\partial v}{\partial z} \right. \\{} & {} \quad \left. + \gamma \frac{\partial w_i}{\partial z} \left( \frac{\partial u}{\partial r} + \frac{\partial v}{\partial z} + \frac{u}{r} \right) \right] rdrdz \\{} & {} \quad = \int _{\Gamma _e} w_i (t_z)rds \end{aligned}$$

(25)

To discretize continuous eqs. 24–25 within each finite element, the velocities (u, v) are approximated by the following trial solution:

$$\begin{aligned} u&= \sum _{j=1}^{n} \psi _j(r,z)u_j \\ v&= \sum _{j=1}^{n} \psi _j(r,z)v_j \end{aligned} $$

(26)

where $u_j$ and $v_j$ are the radial and axial velocity, respectively, at the nodal points of the element. n and $\psi _j$ are the number of nodes in the element and shape function, respectively. As mentioned earlier, in Galerkin weighted residual approach, weight functions are same as shape functions, therefore, $w_i=\psi _i$. Substituting trial solution and weighting function, we write eq. 24 and 25 in compact matrix notation as follows [27]:

$$\begin{aligned}{} & {} \left( 2\mu \left[ S^{rr}\right] +\mu \left[ S^{zz}\right] +2\mu \left[ M\right] \right. \\{} & {} \left. \quad +\gamma \left( \left[ S^{rr}\right] +\left[ S^{ro}\right] +\left[ S^{or}\right] +\left[ M\right] \right) \right) \lbrace u_j \rbrace \\{} & {} \quad + \left( \mu \left[ S^{zr}\right] +\gamma \left[ S^{rz}\right] +\gamma \left[ S^{oz}\right] \right) \lbrace v_j \rbrace = \lbrace F^r \rbrace \end{aligned}$$

(27)

$$\begin{aligned}{} & {} \left( \mu \left[ S^{rz}\right] +\gamma \left[ S^{zr}\right] +\gamma \left[ S^{zo}\right] \right) \lbrace u_j \rbrace \\{} & {} \quad + \left( \mu \left[ S^{rr}\right] +2\mu \left[ S^{zz}\right] +\gamma \left[ S^{zz}\right] \right) \lbrace v_j \rbrace = \lbrace F^z \rbrace \end{aligned}$$

(28)

Eqs. 27–28 are further simplified in matrix notation as follows:

$$\begin{aligned} \begin{bmatrix} \left[ K^{rr}\right] &{} \left[ K^{rz}\right] \\ \left[ K^{zr}\right] &{} \left[ K^{zz}\right] \end{bmatrix} \begin{Bmatrix} \lbrace u_j \rbrace \\ \lbrace v_j \rbrace \end{Bmatrix} = \begin{Bmatrix} \lbrace F^r \rbrace \\ \lbrace F^z \rbrace \end{Bmatrix} \end{aligned}$$

(29)

where,

$$\begin{aligned} \begin{aligned} \left[ K^{rr}\right]&= 2\mu \left[ S^{rr}\right] +\mu \left[ S^{zz}\right] +2\mu \left[ M\right] \\&\quad +\gamma \left( \left[ S^{rr}\right] +\left[ S^{ro}\right] +\left[ S^{or}\right] +\left[ M\right] \right) \\ \left[ K^{rz}\right]&= \mu \left[ S^{zr}\right] +\gamma \left[ S^{rz}\right] +\gamma \left[ S^{oz}\right] \\ \left[ K^{zr}\right]&= \mu \left[ S^{rz}\right] +\gamma \left[ S^{zr}\right] +\gamma \left[ S^{zo}\right] \\ \left[ K^{zz}\right]&= \mu \left[ S^{rr}\right] +2\mu \left[ S^{zz}\right] +\gamma \left[ S^{zz}\right] \end{aligned} \end{aligned}$$

(30)

The element coefficient matrices are defined as follows:

$$\begin{aligned}{} & {} M_{ij} = \int _{\Omega _e} \frac{\psi _i \psi _j}{r}drdz \end{aligned}$$

(31)

$$\begin{aligned}{} & {} \begin{aligned} S_{ij}^{rr} = \int _{\Omega _e} \frac{\partial \psi _i}{\partial r} \frac{\partial \psi _j}{\partial r}rdrdz \quad S_{ij}^{rz} = \int _{\Omega _e} \frac{\partial \psi _i}{\partial r} \frac{\partial \psi _j}{\partial z}rdrdz \end{aligned} \end{aligned}$$

(32)

$$\begin{aligned}{} & {} \begin{aligned} S_{ij}^{zr} = \int _{\Omega _e} \frac{\partial \psi _i}{\partial z} \frac{\partial \psi _j}{\partial r}rdrdz\quad S_{ij}^{zz} = \int _{\Omega _e} \frac{\partial \psi _i}{\partial z} \frac{\partial \psi _j}{\partial z}rdrdz \end{aligned} \end{aligned}$$

(33)

$$\begin{aligned}{} & {} \begin{aligned} S_{ij}^{ro} = \int _{\Omega _e} \frac{\partial \psi _i}{\partial r} \psi _j drdz \quad S_{ij}^{or} = \int _{\Omega _e} \psi _i \frac{\partial \psi _j}{\partial r} drdz \end{aligned} \end{aligned}$$

(34)

$$\begin{aligned}{} & {} \begin{aligned} S_{ij}^{zo} = \int _{\Omega _e} \frac{\partial \psi _i}{\partial z} \psi _j drdz \quad S_{ij}^{oz} = \int _{\Omega _e} \psi _i \frac{\partial \psi _j}{\partial z} drdz \end{aligned} \end{aligned}$$

(35)

$$\begin{aligned}{} & {} \begin{aligned} F_i^r = \int _{\Gamma _e} \psi _i (t_r)rds \quad F_i^z = \int _{\Gamma _e} \psi _i (t_z)rds \end{aligned} \end{aligned}$$

(36)

2.4.2 Velocity-pressure formulation

In velocity-pressure formulation, a natural and direct formulation, the weak form of continuity equation is obtained using weight function, one order less than used for Navier–Stokes equations [27]. Both Navier–Stokes equation physically represents force, hence same weighting function can be used. However, continuity equation represents the volume change. Volume change occur under the action of hydrostatic pressure, hence weight function ($w_{2k}$) for continuity, equation should like the pressure (P) or the shape function of pressure. The weak form of the continuity equation can be written as follows [27]:

$$\begin{aligned} - \int _{\Omega _e} w_{2k} \left[ \frac{\partial u}{\partial r} + \frac{\partial v}{\partial z} + \frac{u}{r} \right] rdrdz = 0 \end{aligned}$$

(37)

The minus sign is inserted to make the resulting finite element model symmetric. Equation 37 is rewritten as follows,

$$\begin{aligned} - \int _{\Omega _e} \left[ w_{2k} \frac{\partial u}{\partial r} + w_{2k} \frac{\partial v}{\partial z} + w_{2k} \frac{\partial u}{\partial r} \right] rdrdz= 0 \end{aligned}$$

(38)

Substituting components of stress tensor from eqs. 9, 10, 11 and 12 in eqs. 21 and 22, the following equations are obtained:

$$\begin{aligned}{} & {} \int _{\Omega _e} \left[ 2\mu \frac{\partial w_i}{\partial r} \frac{\partial u}{\partial r} + \mu \frac{\partial w_i}{\partial z} \left( \frac{\partial u}{\partial z} + \frac{\partial v}{\partial r} \right) \right. \\{} & {} \quad \left. + 2\mu \frac{w_i}{r} \frac{u}{r} - \frac{\partial w_i}{\partial r}P - \frac{w_i}{r}P \right] rdrdz \\{} & {} \quad = \int _{\Gamma _e} w_i (t_r)rds \end{aligned}$$

(39)

$$\begin{aligned}{} & {} \int _{\Omega _e} \left[ \mu \frac{\partial w_i}{\partial r} \frac{\partial u}{\partial z} + \mu \frac{\partial w_i}{\partial r} \frac{\partial v}{\partial r} \right. \\{} & {} \quad \left. + 2\mu \frac{\partial w_i}{\partial z} \frac{\partial v}{\partial z} - \frac{\partial w_i}{\partial z}P \right] rdrdz= \int _{\Gamma _e} w_i (t_z)rds \end{aligned}$$

(40)

To discretize continuous eqs. 39–40 within each finite element, the velocities (u, v) are approximated by the trial solution defined in eq. 26 and pressure (P) is approximated by following trial solution, that is one order less than used for the velocities:

$$\begin{aligned} P = \sum _{l=1}^{m} \phi _l(r,z)P_l \end{aligned}$$

(41)

where $P_l$ is the pressure at the corner nodal points of the element. m and $\phi _l$ are the number of corner nodes in the element and shape functions respectively. As explained before, in Galerkin weighted residual approach, $w_i=\psi _i$ and $w_{2k}= \phi _l$. On putting trial solution and weighting function, we can write eqs. 39, 40 and 38 in compact matrix notation as follows:

$$\begin{aligned}{} & {} \left( 2\mu \left[ S^{rr}\right] +\mu \left[ S^{zz}\right] +2\mu \left[ M\right] \right) \lbrace u_j \rbrace + \left( \mu \left[ S^{zr}\right] \right) \lbrace v_j \rbrace \\{} & {} \quad - \left( \left[ G^{ro}\right] +\left[ G^{oo}\right] \right) \lbrace P_l \rbrace = \lbrace F^r \rbrace \end{aligned}$$

(42)

$$\begin{aligned}{} & {} \left( \mu \left[ S^{rz}\right] \right) \lbrace u_j \rbrace + \left( \mu \left[ S^{rr}\right] +2\mu \left[ S^{zz}\right] \right) \lbrace v_j \rbrace \\{} & {} \quad - \left( \left[ G^{zo}\right] \right) \lbrace P_l \rbrace = \lbrace F^z \rbrace \end{aligned}$$

(43)

$$\begin{aligned}{} & {} - \left( \left[ G^{ro}\right] ^T+\left[ G^{oo}\right] ^T\right) \lbrace u_j \rbrace - \left( \left[ G^{zo}\right] ^T\right) \lbrace v_j \rbrace = 0 \end{aligned}$$

(44)

Further, we can write above three equations in more simplified way in matrix form as follows:

$$\begin{aligned} \begin{bmatrix} \left[ K^{rr}\right] &{} \left[ K^{rz}\right] &{} \left[ K^{ro}\right] \\ \left[ K^{zr}\right] &{} \left[ K^{zz}\right] &{} \left[ K^{zo}\right] \\ \left[ K^{or}\right] &{} \left[ K^{oz}\right] &{} \left[ 0\right] \end{bmatrix} \begin{Bmatrix} \lbrace u \rbrace \\ \lbrace v \rbrace \\ \lbrace P \rbrace \end{Bmatrix} = \begin{Bmatrix} \lbrace F^r \rbrace \\ \lbrace F^z \rbrace \\ \lbrace 0 \rbrace \end{Bmatrix} \end{aligned}$$

(45)

where,

$$\begin{aligned} \begin{aligned} \left[ K^{rr}\right]&= 2\mu \left[ S^{rr}\right] +\mu \left[ S^{zz}\right] +2\mu \left[ M\right] \\ \left[ K^{rz}\right]&= \mu \left[ S^{zr}\right] \\ \left[ K^{ro}\right]&= - \left( \left[ G^{ro}\right] +\left[ G^{oo}\right] \right) \\ \left[ K^{zr}\right]&= \mu \left[ S^{rz}\right] \\ \left[ K^{zz}\right]&= \mu \left[ S^{rr}\right] +2\mu \left[ S^{zz}\right] \\ \left[ K^{zo}\right]&= -\left[ G^{zo}\right] \\ \left[ K^{or}\right]&= - \left( \left[ G^{ro}\right] ^T+\left[ G^{oo}\right] ^T\right) \\ \left[ K^{oz}\right]&= -\left[ G^{zo}\right] ^T \end{aligned} \end{aligned}$$

(46)

where the [S], [M] and $\lbrace F \rbrace$ element coefficient matrices are defined as before from eq. 31 to eq. 36. The remaining element coefficient matrices are defined as follows:

$$\begin{aligned}{} & {} G_{kl}^{ro} = \int _{\Omega _e} \frac{\partial \psi _k}{\partial r} \phi _l rdrdz \end{aligned}$$

(47)

$$\begin{aligned}{} & {} G_{kl}^{zo} = \int _{\Omega _e} \frac{\partial \psi _k}{\partial z} \phi _l rdrdz \end{aligned}$$

(48)

$$\begin{aligned}{} & {} G_{kl}^{oo} = \int _{\Omega _e} \psi _k \phi _l drdz \end{aligned}$$

(49)

2.4.3 Mesh generation and evaluation of element coefficient matrices

A six node triangular element (figure 3a) was chosen over three-node element as it improves the solution accuracy and reduce the overall solution time by reducing the number element required. Quadratic and linear shape functions were used to compute velocity and pressure field, respectively. A three-node triangular mesh inside the droplet domain was generated using Matlab® function ‘initmesh’. To generate six-node mesh, we developed an in-house code, which places a node at the exact midpoint of the each side of triangular element and updates the point matrix, element connectivity matrix, boundary matrix. The mesh generated using MATLAB function ‘initmesh’ and modified using in-house code is shown in figure 3(b).

Figure 3

(a) Six-node triangular element. (b) Six-node mesh in droplet domain and red dots represent nodes.

In order to evaluate the integrals of element coefficient matrices, numerical integration was employed. To do numerical integration, first we need to map real element in (r, z) coordinates to a master or parent element in generic ($\xi$, $\eta$) coordinates over which integration will performed using Gaussian quadrature points. As in our real element all three nodes located at side of triangle are located at mid-point of each triangle side, so it is sufficient to use linear shape function to do coordinate transformation. The following expression facilitates the (r, z) to ($\xi$, $\eta$)coordinate transformation:

$$\begin{aligned} \begin{aligned} r = \sum _{k=1}^{3} r_k \phi _k (\xi , \eta )\quad z = \sum _{k=1}^{3} z_k \phi _k (\xi , \eta ) \end{aligned} \end{aligned}$$

(50)

where $r_k$ and $z_k$ is $k_{th}$ radial and axial coordinates of corner nodes of the triangle element. Shape functions $\phi _k$ can be defined as follows:

$$\begin{aligned} \begin{aligned} \phi _1&= \xi \\ \phi _2&= \eta \\ \phi _3&= 1-\eta -\xi \end{aligned} \end{aligned}$$

(51)

To evaluate integrals, the following expression is required to map infinitesimal area of real element to corresponding area of parent element:

$$\begin{aligned} drdz = \text {det}\left( Jc\right) d\xi d\eta \end{aligned}$$

(52)

where $\text {det}(Jc)$ is the determinant of the Jacobian (Jc) for the element under consideration and is defined as follows:

$$\begin{aligned} \left[ Jc\right] = \begin{bmatrix} \frac{\partial r}{\partial \xi } &{} \frac{\partial z}{\partial \xi }\\ \frac{\partial r}{\partial \eta } &{} \frac{\partial z}{\partial \eta } \end{bmatrix} \end{aligned}$$

(53)

For linear mapping $\text {det}(Jc)$ is equal to 2 times of the area of triangle in consideration. Next, we need to convert partial derivative of (r, z) into derivatives of ($\xi$,$\eta$) which is done using the following relationship:

$$\begin{aligned} \begin{Bmatrix} \frac{\partial \psi _i}{\partial r}\\ \frac{\partial \psi _i}{\partial z} \end{Bmatrix} =\left[ Jc\right] ^{-1} \begin{Bmatrix} \frac{\partial \psi _i}{\partial \xi }\\ \frac{\partial \psi _i}{\partial \eta } \end{Bmatrix} \end{aligned}$$

(54)

where shape function $\psi _i$ is quadratic shape function for a six-node triangle element as mentioned before. Quadratic shape function is defined as follows:

$$\begin{aligned} \begin{aligned} \psi _1&= 2\xi ^2-\xi \\ \psi _2&= 2\eta ^2-\eta \\ \psi _3&= 1-3\xi -3\eta +4\xi \eta +2\xi ^2+2\eta ^2\\ \psi _4&= 4\xi \eta \\ \psi _5&= 4(\eta -\xi \eta -\eta ^2)\\ \psi _6&= 4(\xi -\xi \eta -\xi ^2) \end{aligned} \end{aligned}$$

(55)

Using eqs. 52, 54 and 55, the integrals specified in equations from eqs. 31 to 35 can be converted to ($\xi$,$\eta$) coordinates and numerical integration can be performed using Gaussian quadrature as follows:

$$\begin{aligned} \int _{\Omega _e}f(\xi , \eta ) d\xi d\eta \cong \frac{1}{2} \sum _{l=1}^{gp} w_l f(\xi _l, \eta _l) \end{aligned}$$

(56)

where $f(\xi , \eta )$ is any function in ($\xi$, $\eta$) coordinates and ($\xi _l$, $\eta _l$) are the Gaussian points [27]. gp is the number of Gaussian points used to evaluate the integral. Three and one-point Gaussian quadrature was used to evaluate integrals.

To calculate coefficient of force vector on the right hand side of eq. 29 or to apply stress boundary condition on the boundary of the domain, we need to transform the boundary or open side of the triangle to one dimensional line coordinate (s) whose origin at first point of boundary. As we are using six-node or quadratic triangular element, we have three nodes on each side of the triangle, so we need to use quadratic shape function ($\psi _{bi}$). These three shape functions ($\psi _{bi}$) can be defined as follows:

$$\begin{aligned} \begin{aligned} \psi _{b1}&= \left( 1-\frac{s}{h}\right) \left( 1-\frac{2s}{h}\right) \\ \psi _{b2}&= \frac{4s}{h}\left( 1-\frac{s}{h}\right) \\ \psi _{b3}&= -\frac{s}{h}\left( 1-\frac{2s}{h}\right) \end{aligned} \end{aligned}$$

(57)

where h is the length of the side or boundary of the element. The elements which are inside the domain, for them, the value of coefficients in force vector are need not to be calculated as the force acting on the side or boundary of the neighboring elements cancels out each other. Therefore, we need to calculate coefficient of force vector only at the boundary of elements that are located at boundary of the domain and some external force or stress is applied.

2.4.4 Liquid–gas interface boundary conditions

The boundary conditions at liquid–gas interface, as described in section 2.3, are applied using the following approach. As the shape of droplet is spherical cap, the liquid–gas interface is not parallel to r or z axis. To apply the both boundary conditions precisely, coordinate rotation must be done for the nodes at the liquid–gas interface of the droplet [27], which can be done with the help of rotation matrix [Q]. Equation 29 can be written in more compact form as follows:

$$\begin{aligned} \left[ K\right] \lbrace u \rbrace = \lbrace F \rbrace \end{aligned}$$

(58)

To perform the coordinate rotation on the nodes at the liquid–gas interface of the droplet following mathematical operation can be done:

$$\begin{aligned} \left[ Q\right] ^T\left[ K\right] \left[ Q\right] \lbrace u \rbrace = \lbrace F \rbrace \end{aligned}$$

(59)

where rotation matrix [Q] can be defined as follows:

$$\begin{aligned} \left[ Q\right] = \begin{bmatrix} \ddots &{} \cdots &{} \cdots &{} \cdots \\ \cdots &{} n_{r,i} &{} n_{z,i} &{} \cdots \\ \cdots &{} -n_{z,i} &{} n_{r,i} &{} \cdots \\ \cdots &{} \cdots &{} \cdots &{} \ddots \\ \end{bmatrix} \end{aligned}$$

(60)

where $n_{r,i}$ and $n_{z,i}$ are the normal vector in radial and axial direction for $i_{th}$ node on the liquid–gas interface.

2.4.5 Algorithm

The algorithm was implemented in Matlab® [28] and the flow chart of the algorithm is shown in figure 4. The sequential steps in the algorithm are as follows:

• 1. Solve the evaporation mass flux on liquid–gas interface (j) by a two-way coupling [20] between heat transport inside droplet-substrate and mass transport of liquid vapor in surrounding air (figure 2).

• 2. Calculate ${\dot{m}}$, dH/dt and $\partial h/\partial t$ using eqs. 5, 16 and 18, respectively.

• 3. Calculate velocity boundary condition at liquid–gas interface using eq. 13 and data obtained in steps 1 and 2.

• 4. Generate six node mesh inside the droplet domain.

• 5. Calculate element coefficients defined in section 2.4.1 or section 2.4.2 using numerical integration technique explained in section 2.4.3 for six node triangular elements.

• 6. Assemble K and F matrices given by eq. 29 or eq. 45 for penalty function or Velocity-pressure formulation, respectively.

• 7. Apply boundary conditions on the boundary nodes in the assembled matrices (section 2.4.4).

• 8. Solve system of equations ($Ax = b$) for u, v and P using inbuilt solver backslash (\) in Matlab®.

Figure 4

Flow chart of the solver.

3 Testing of the solver

We have used two formulations (Penalty function formulation and Velocity-pressure formulation) to solve flow field inside the droplet. Here, we are presenting validation for these both formulations. We consider evaporation of a microliter water droplet on a heated and non-heated copper substrate. The values of the thermophysical properties and parameters used in the present study are given in table 1.

Table 1 Thermophysical properties and parameters used in the present study

3.1 Grid-size independence test

In order to achieve grid size convergence, we test six grids with respect to most refined grid using penalty function formulation. Number of nodes in computational domain of droplet are listed in table 2. We compute L2-norm error ($\epsilon$) with respect to the most refined mesh is expressed as follows:

$$\begin{aligned} \epsilon = \left[ \frac{1}{N^2} \sum _{i=1}^{N} \left( u_i^N - u_i^{N_{max}} \right) \right] ^{1/2} \end{aligned}$$

(61)

where i represents the indices of grid points of the mesh and N is the number of nodes in the considered mesh. $N_{max}$ is number of nodes in the most refined mesh ($N_{max} = 15865$) and represents the reference solution. Figure 5 shows $L^2$-norm error of a solution variable (radial velocity u, axial velocity v and pressure p) as function of number of nodes in the computational domain. As figure 5 shows, $L^2$-norm error for radial velocity (u), axial velocity (v) and pressure (P) solutions for different mesh follows the slope of the slope-2 line. Therefore, we can conclude that our solutions are second-order accurate and grid independent.

Table 2 Number of nodes in different grids used in grid-size convergence study

Figure 5

Grid-size independence test: L2-norm errors of radial velocity (u), axial velocity (v) and pressure (P) are plotted with respect to different grids tested. A dashed line of slope 2 is plotted for reference.

3.2 Code validation

We validate the code by comparing flow field inside the droplet with the published data. Computed velocity profiles obtained using different formulations are compared in figure 6. The published data is also plotted in this figure. At radial location $r=0.1$ mm, maximum velocity is $0.13 \times 10^{-3}$ mm/s and as fluid move radially outward at location $r=0.6$ and 0.9 mm radial velocity of fluid increases to $0.8 \times 10^{-3}$ mm/s and $1.6 \times 10^{-3}$ mm/s, respectively. However, in axial direction, from $z=0$ to liquid-air interface of droplet, first, droplet velocity increases with the increase of axial distance and after attaining a maximum value it starts decreasing. To validate the code radial velocity at different radial location along the height of the droplet has been compared with results of model of Hu and Larson [26]. Figure 6 shows the radial velocity (u) profiles calculated along axial direction (z) at different radial locations, $r=0.1$, 0.6 and 0.9 mm, using Velocity-pressure and Penalty function formulation with direct approach of applying boundary conditions. These profiles were compared with the profiles obtained by Hu and Larson [26]. The radial velocity profile obtained from present models are in good agreement with the profiles obtained by Hu and Larson [26].

Figure 6

Validation of penalty function (PF) and velocity-pressure (VP) formulation. Comparison of radial velocity profiles at different radial locations obtained from present model with data of Hu and Larson [26].

3.3 Computational time

Figure 7 shows the comparison of computational time taken by both formulations. These computations were performed on a computer having following specifications; 4.84 GHz, 8-core Intel core i9 processor, 64 GB RAM, SSD data storage. As the number of computational nodes increases computational time increases non-linearly for the both formulations. However, velocity pressure formulation consumes more computational time as compared to penalty function formulation and as the number of nodes increases computational time difference for velocity pressure formulation with respect to the penalty function formulation also increases for the computation performed on the same number of nodes. Which concludes that velocity pressure formulation gets slower with increment of number of nodes. Hence, it is preferable to use the penalty function formulation in order to save the computational cost and time.

Figure 7

Comparison of computational time taken by penalty function (PF) and velocity pressure (VP) formulation, with respect to number of nodes.

3.4 Flow and pressure field on a non-heated and heated substrate

Figure 8a shows the computed streamlines and contours of radial velocity (u) using penalty function formulation. The streamlines start from the apex of the droplet and end in the the region close to contact line, implying a radially outward flow inside the droplet. Contours of radial velocity (u), plotted in figure 8a indicate that in the central region the flow velocity ($\sim$0.6 $\upmu \hbox{m}$/s) is much slower than near the contact line region ($\sim$1.6 $\upmu \hbox{m}$/s). Therefore, u increases from droplet interior to the contact line and the maximum u occurs near the contact line. This is attributed to the largest evaporation mass flux j near the contact line, which results in larger mass loss near the contact line. The fluid from the interior of the droplet rushes towards the contact line to maintain droplet spherical cap shape, dictated by the surface tension forces [5, 21]. On a heated substrate, a larger j and ${\dot{m}}$ accelerate the evaporation and reduces the total evaporation time of the droplet, consistent with prior experiments [20, 29].

Figure 8(b) shows the axial velocity (v) contour inside the evaporating droplet. The minus (−) sign represents the downward axial direction of the flow. The magnitude of v decreases from liquid–gas interface to liquids–solid interface, which implies that as the liquid moves from liquid–gas interface towards substrate or contact line region, the axial velocity decelerates. Comparison of figure 8(a) and b show that the axial velocity is smaller than radial velocity, suggesting a dominating flow in the radial direction compared to axial direction. This fact is also confirmed by direction of the streamlines. Figure 8(c) shows contours of computed pressure (P) inside the droplet. The pressure is the lowest near the contact line due to the largest velocity in this region.

Figure 8

(a) Streamlines and contours of radial velocity (u) inside the evaporating droplet (b) Contours of axial velocity (v) inside the evaporating droplet (c) Contours of pressure field (P) inside the evaporating droplet.

Figure 9 shows radial velocity (u) profiles at different radial locations, when droplet is placed on a heated substrate. Each frame of figure 9 plots the variation of radial velocity with respect to axial coordinate of the droplet for different cases of substrate temperatures and fixed radial locations $r=0.3$, 0.5, 0.7 and 0.9 mm. At axial location, $z=0$, radial velocity is zero for all cases and at all radial locations, due to zero slip condition. As axial location increases, radial velocity initially increases and reaches to a maximum value before it slightly decreases. With the increase in substrate temperature, radial velocity at any fixed axial location increases at all radial location inside the droplet. As the substrate temperature increases, it results in overall increase of liquid–gas interface temperature. This promotes the larger vapor concentration at the liquid–gas interface and consequently, mass loss is larger from the interface. Hence, it results in a larger evaporation rate (j), thereby increasing the liquid–gas interface normal velocity ($u_n$) defined by eq. 13 and resulting in larger radial velocity (u) inside the droplet.

Figure 9

Radial velocity (u) profiles at different radial locations for a droplet evaporating on a heated substrate.

Lastly, we discuss the effect of flow field inside a droplet on a heated substrate on self-assembly of colloidal particles, if present in the droplet. Studies have shown a departure from a typical ring-like pattern formed by colloidal particles to a thinner ring and central deposit of particles on a heated surface [29]. Similar patterns of deposits have been obtained for a initially-heated droplet on substrate at ambient temperature [30] and on a non-uniformly heated substrate [31]. In general, these changes in the pattern have been attributed to evaporation-driven flow and flow driven by Marangoni stress along the liquid–gas interface. The pinning or depinning of the contact line by colloidal particles also play an important role in this context [31].

4 Conclusions

We have presented the development of a finite element solver for computing fluid flow inside an evaporating sessile droplet. The evaporation is considered as quasi-steady with a pinned contact line. Galerkin weighted residual approach is used to formulate weak form of the numerical equations. Penalty function and velocity-pressure formulation are applied to discretise the Navier–Stokes equation in cylindrical coordinates. Six-node triangular mesh is used for higher accuracy of the solution. The solver shows a second order accuracy in grid-size convergence study. Results obtained from the simulations are compared with prior numerical results and found to be in good agreement. Both formulations show similar accuracy in the computed results. However, since penalty function formulation uses one lesser degree of freedom on each node compared to velocity-pressure formulation, resulting in lesser computational time in the former as compared to latter. The solver is tested for simulating the evaporation of a sessile microliter droplet on a heated copper substrate. The future development will involve the implementation of Marangoni stress and buoyancy terms in the FE solver.