Modeling of Gold Adsorption by the Surface of Defect Graphene

Abstract

The results of the theoretical investigation of the local structural changes and adsorption characteristics of the graphene (GP) surface in the presence of a vacancy + Au_ads adatom complex are presented. Based on the density functional theory (DFT), the adsorption properties of Au_ads at the surface of GP supercells containing 50 carbon atoms with vacancies $({\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle ,{\text{ G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$) are calculated. The most stable configuration of ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercells with a vacancy + Au_ads adatom complex is determined. The effect that an Au_ads adatom has on the band structure and local magnetic moment in ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ is calculated. The data are analyzed based on the equilibrium atomic configuration ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$, local density of electronic states, and spin polarization. The calculations are made using the exchange-correlation functional in a local electron-spin density approximation (LSDA).

1 INTRODUCTION

Graphene (GP) is studied as a promising material for, e.g., the formation of a two-dimensional substrate in nanoelectronics and spintronics. There are known experimental [1–3] and theoretical [4–10] data on the investigation of the adsorption of different metals, in particular, gold, on the GP surface.

The adsorption of atoms (adatoms) by the GP surface is an efficient technique for the polarization of charge carriers [2]. Studies of magnetism in GP revealed that the formation of a local magnetic moment in GP depends on both the concentration and geometry of the defects at the surface [3].

The ab initio calculations of the adsorption of metals, in particular, gold (Au_ads) by the GP surface ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ [4–10] show that the calculated characteristics (adsorption energy [4–8] and magnetic moment [6]) depend on varied factors: the calculation technique [5, 9], adatom structure [7], adsorption site (top, bridge, or hollow position) [4, 5], distance of bond (d) between an adatom and surface [5, 8], character of interaction between the adatom and GP [6–9], and substrate structure [9, 10].

In the well-known studies on Au_ads adsorption by the GP surface, defect-free GP was mainly studied using different exchange-correlation functionals (E_XC). However, as is well known, surface defects noticeably affect the electronic, magnetic, and mechanical properties of the surface. Taking this into account, studies of the adsorption and electronic properties of the surface in the presence of a vacancy + Au_ads adatom complex for the ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ structure based on GP are topical.

The aim of this study is the ab initio calculation of the energy of Au_ads adsorption by the surface of GP supercells ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercells with point defects (V denotes a vacancy).

2 MODEL AND CALCULATION PROCEDURE

Calculations of the band structure of the systems based on defective GP were carried out using the DFT. Supercells of GP with adsorbed Au ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$, containing a vacancy were studied. The calculations were performed using the Atomistix ToolKit program package at a temperature of T = 0 K [11, 12]. GP supercells containing 50 carbon atoms were used.

The electronic configuration of a free atom is required for the correct description of the chemical bond in the system. The following electronic configurations were used for atoms: Au for [Xe]4f  ¹⁴4d¹⁰4s¹ and C for [He]2s²2p². The [Xe] and [He] states are core states. A ground state of both gold (4f  ¹⁴4d¹⁰4s¹) and carbon (2s²2p²) atoms is a state with an open shell. For such states, effects of spin polarizarion were considered.

The exchange-correlation functional E_XC was calculated in a local electron-spin density approximation (LSDA) in the Perdew–Zunger parameterization [13]. In the calculations, a GP lattice constant equal to its LDA optimized value was used. For integration in the reciprocal space, the Monkhorst–Pack scheme [14] with a grid of 5 × 5 × 5 k points in the Brillouin zone was applied.

The electronic structure of ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercells with a size of 5 × 5 was calculated taking into account the ground states of Au and carbon atoms in the k‑points of graphene supercell samples in the Brillouin zone along the M–Γ–K–M lines. This makes it possible to trace the dispersion of the Dirac points at the edges of the Brillouin zone.

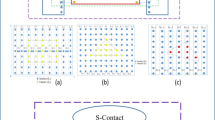
The DFT calculations were carried out for three different sites of Au_ads(111) adsorption on GP [4]: the bridge position (B site, Au_ads is located in a bridge region of the С–С bond on GP), hollows at the center (H site, Au_ads is located at the center of a six-member ring of the С–С bond on GP), and top position of an adatom (T site, Au_ads is located in the tetrahedral configuration of the С–С bond in GP) (Fig. 1).

Fig. 1.

Adsorption sites of the 5 × 5 supercell of a GP monolayer. B site (bridge position; location at the center of the C–C bond); T site (tetrahedral site; location on top); H site (hexagonal site; location at the center of a six-member ring): (a) defect-free GP, (b) GP containing one vacancy, and (c) GP containing one vacancy and adatoms.

Fig. 1.

(Contd.)

Calculations of the energy of adsorption of Au_ads adatoms and magnetic properties at the surface of GP structures were made in optimized GP supercells. The kinetic cutoff energy in the exchange correlation was 500 eV, which provided the convergence for the total energy of 10⁻⁵ eV/cell. Each studied supercell was relaxed earlier with the maximum tolerance of 0.01 eV/Å for force, 0.01 eV/ų for voltage, and the maximal shift of 0.001 Å, respectively.

The energy of Au_ads adatom adsorption was calculated using the formula [12]

$$\begin{gathered} E_{{{\text{ads}}}}^{{{\text{atom}}}} = \frac{1}{{m + n}}~{{E}_{{{\text{total}}}}}\left( {{\text{graphene}} + {\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right) \\ - \,\,\left[ {mE_{{{\text{iso}}}}^{{\text{C}}}\left( {{\text{graphene}}} \right) + nE_{{{\text{iso}}}}^{{{\text{Au}}}}\left( {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right)} \right], \\ \end{gathered} $$

(1)

where $E_{{{\text{ads}}}}^{{{\text{atom}}}}$ is the energy of the Au_ads adatom bonding with the GP surface, ${{E}_{{{\text{total}}}}}\left( {{\text{graphene}} + {\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right)$ is the total energy of the $\left( {{\text{graphene}} + {\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right)$ complex, i.e., crystalline GP with an adsorbed atom, $mE_{{{\text{iso}}}}^{{\text{C}}}\left( {{\text{graphene}}} \right)$ is the total energy of isolated GP, and $E_{{{\text{iso}}}}^{{{\text{Au}}}}\left( {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right)$ is the total energy of the isolated Au_ads adatom, as well as and m and n numerate carbon and adatom atoms in GP, respectively. The energy of an isolated atom in a vacuum box, whose sizes coincided with the sizes of the supercell of a crystalline GP plate.

Deformation of the GP monolayers during the adsorption of gold Au_ads(111) was calculated using the formula: $\frac{{d_{{{\text{C}} - {\text{C}}}}^{{{\text{free}}}} - d_{{{\text{C}} - {\text{C}}}}^{{{\text{ads}}}}}}{{d_{{{\text{C}} - {\text{C}}}}^{{{\text{free}}}}}}\,\,~ \times \,\,100$, where $d_{{{\text{C}} - {\text{C}}}}^{{{\text{free}}}}$ and $d_{{{\text{C}} - {\text{C}}}}^{{{\text{ads}}}}$ are the C–C bond lengths in pure GP and GP monolayers with adsorbed atoms, respectively.

The total and partial magnetic moments were estimated using the known technique. The exchange integrals in the Hamiltonian are taken into account in the following form: $H = ~\,\, - \sum\nolimits_{i \ne j} {{{J}_{{ij}}}{{{\text{S}}}_{i}}{{{\text{S}}}_{j}}}$, where ${{J}_{{ij}}}$ are the parameters of the magnetic exchange interaction between i and j atoms, and S_i is the total spin of atom i. The magnetic moment of atom i is related to the spin S_i by the following relationship: ${{M}_{i}} = g{{\mu }_{{\text{B}}}}{{{\text{S}}}_{i}}$, where $g$ is the Landé factor (gyromagnetic factor) and ${{\mu }_{{\text{B}}}}$ is the Bohr magneton (elementary magnetic moment).

3 RESULTS AND DISCUSSION

As is well known, in GP, each carbon atom is bonded to the other three carbon atoms. In accordance with the sp² hybridization of a carbon atom, which has two 2s and two 2p electrons in the valence state, the С–С bond length in GP changes.

According to the DFT calculations using the LDA (local density approximation) E_XC, the С–С bond length in pure GP (1.41 Å) was shorter than the C–Au bond length in the ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ structures studied by us.

3.1 Adsorption

The binding energy $E_{{{\text{ads}}}}^{{{\text{atom}}}}$ between the adatom and the surface depends on, e.g., the bond length (d) between the adatom and the surface. Evidently, if the average d length is large, then $E_{{{\text{ads}}}}^{{{\text{atom}}}}$ should be low. In the case of a large length of the bond between the adatom and the surface, physical adsorption takes place. If the bond length is short, then $E_{{{\text{ads}}}}^{{{\text{atom}}}}$ should rise due to the chemical adsorption.

The Au adsorption on GP depends on the time (t) of residence of the adatom and the distance (λ) passed by it to the substrate before desorption. These values are related to the energies of atoms for desorption $E_{{{\text{ads}}}}^{{{\text{atom}}}}$ and surface diffusion $E_{{\text{d}}}^{{{\text{atom}}}}$ by the relationship

$$\tau = \,\,~\nu _{{{\text{ads}}}}^{{ - 1}}~{\text{exp}}\left( {\frac{{E_{{{\text{ads}}}}^{{{\text{atom}}}}}}{{{{k}_{{\text{B}}}}T}}} \right),$$

(2)

where ${{\nu }_{{{\text{ads}}}}}$ is the frequency of desorption attempts, ${{k}_{{\text{B}}}}$ is the Boltzmann constant, and $T$ is temperature. Then we can write for λ

$$\lambda = ~\frac{a}{2}~\sqrt {\frac{{{{\;}}{{\nu }_{{\text{d}}}}}}{{{{\;}}{{\nu }_{{{\text{ads}}}}}}}} ~{\text{exp}}\left( {\frac{{E_{{{\text{ads}}}}^{{{\text{atom}}}} - E_{{\text{d}}}^{{{\text{atom}}}}}}{{2{{k}_{{\text{B}}}}T}}} \right),$$

(3)

where a is the distance of one atomic jump and ${{\nu }_{{\text{d}}}}$ is the frequency of diffusion attempts. Taking into account the experimental data on the kinetics of the deposition from the vapor phase and growth of Au particles on the graphite thin films [15, 16], the length λ for Au, e.g., at room temperature, is ∼400 nm. Taking this inti account and comsidering (3), for the adsorption of gold on graphite, the experimental value was obtained: $E_{{{\text{ads}}}}^{{{\text{atom}}}}$ = –0.64 eV.

The ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ atomic structures were earlier relaxed by the DFT LDA technique. Originally, the Au atom was located at at a distance of 2.5 Å from the GP surface and the GP monolayer was “frozen.” At the end of the relaxation, the sum of all forces acting in the system was ≤0.001 eV/Å. The ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ atomic structures for three different configurations (B site, H site, and T site) of Au_ads after relaxation were compared.

The deformation of the GP monolayer for Au_ads adsorption is small. The established equilibrium parameters of lattices, as well as the positions of carbon atoms in GP and the Au_ads adatom agree, with the known data [4–7]. The bond lengths between carbon atoms in GP and the distances between atomic pairs Au–C for the ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ systems after relaxation are determined. In the ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ system, the average distance between carbon and gold atoms was $d_{{{\text{eq}}}}^{{\text{T}}}$ = 2.56 Å for the binding position of Au–C atoms on top (T site). This agrees with the data $d_{{{\text{eq}}}}^{{\text{T}}}$ = 2.61 Å [7].

Figure 2 shows the scheme of a 5 × 5 ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercells optimized by us. In this case the binding energy characterizes the difference in energies of the relaxed GP structure in relation to that of the similar GP structure in which one Au atom is place in a vacuum.

Fig. 2.

Geometrical model of location of an Au_ads adatom on a 5 × 5 monolayer of the GP supercell containing 50 carbon atoms: (a) ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ GP supercell with Au_ads located in the bridge region (B site) between the С–С bond, (b) defect-free GP supercell containing one vacancy ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$, where Au_ads is located in the bridge region (B site) between the С–С bond, and (c) defective GP supercell ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ containing one vacancy, where Au_ads is located on top (T site) over a carbon atom.

The initial position of an Au_ads(111) adatom at the GP surface after relaxation of the${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ system changes slightly. This is due to the fact that an adsorbed Au_ads (111) atom creates a region of local compression of the surface with a ${\text{G}}{{{\text{P}}}_{{\text{V}}}}$ vacancy.

The adsorption energies $E_{{{\text{ads}}}}^{{{\text{atom}}}}$ were compared for the Au_ads adsorbed in three positions: on the top (T site), bridge (B site), and hollow (H site). For the ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ systems, the configurations of atomic binding for Au_ads–C with an adatom turned out to be more stable for the position on top (T site).

Calculations of $E_{{{\text{ads}}}}^{{{\text{atom}}}}$ for Au_ads adatoms at the GP surface using the LDA functional result in slightly overrated $E_{{{\text{ads}}}}^{{{\text{atom}}}}$ values in comparison with those obtained using LSDA data. Taking into account the spin polarization in the LSDA calculations makes it possible to correct the LDA calculated $E_{{{\text{ads}}}}^{{{\text{atom}}}}$ value.

With allowance for the spin splitting for the gold atom, the energy of exchange interaction in ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ was corrected. In this case, the LSDA-calculated $E_{{{\text{ads}}}}^{{{\text{atom}}}}$ value decreases, which is in reasonable agreement with the calculations [4, 5].

Table 1 shows the results of our DFT-LSDA calculations for 5 × 5 ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercells based on GP in comparison with the known data.

Table 1. DFT LSDA-calculated adsorption energies of Au_ads adatom (eV/atom) on 5 × 5 ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercells and average equilibrium distance ($d_{{{\text{eq}}}}^{{\text{T}}}$) between Au–C atoms. The LSDA data are shown for the binding place of Au–C atoms, where an Au_ads adatom is located on top (T site) of the surface

The results of the calculation of $E_{{{\text{ads}}}}^{{{\text{atom}}}}$ for a supercell based on defect-free graphene ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ are similar to the results of the studies [4, 5]. The $E_{{{\text{ads}}}}^{{{\text{atom}}}}$ of an Au_ads adatom in the bridge (B site) and hollow (H site) positions are degenerate values; i.e., Au_ads can easily diffuse to the GP surface in the ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ system from the top.

The calculated equilibrium $d_{{{\text{eq}}}}^{{\text{T}}}$(Å) distance between an Au_ads adatom and the nearest C atom at the GP plane is 2.56 Å, which agrees with the data [4–8]. The calculated $d_{{{\text{eq}}}}^{{\text{T}}}$(Å) distance weakly depends on the functional used in the DFT the calculation. The $d_{{{\text{eq}}}}^{{\text{T}}}$(Å) value is smaller for the ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ system with a GP monovacancy than for a defect-free GP ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$.

As is seen from Table 1, the energy of Au_ads adsorption by GP with a single vacancy ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ is almost an order of magnitude lower, than that on pure GP ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$. This effect of stabilization of the structure is caused by the hybridization of the d orbitals of Au: [Xe]4f  ¹⁴4d¹⁰4s¹ with sp² dangling bonds, present in the neighboring carbon atoms of GP with a single vacancy.

3.2 Energy of the Formation of Defects

Under real conditions, any crystal is nonideal and contains various defects. And the properties, in particular, the mechanical, electrophysical, optical, and physical properties of solid-state materials, depend on the concentration and energy of the formation of different types of defects.

If there is a vacancy on the surface near the adsorbed atom, the movement of atoms (both adsorbed and intrinsic) is probably through the vacancy mechanism. The higher the concentration of vacancies in a crystal the higher the probability of the “near” position of a vacancy. Since the energy of binding for impurity and intrinsic atoms with lattice atoms is different, the rates of heterodiffusion and self-diffusion will also be different. Evidently, the rate of diffusion through the vacancy mechanism is mainly determined by the concentration and energy of point defects.

The energy of the vacancy formation was calculated [11] in the case of a GP with a single vacancy (SV):

$$E_{f}^{{{\text{SV}}}} = E\left( {{\text{SV}} - {\text{graphene}}} \right) - ~\frac{{\left( {m - 1} \right)}}{m}E\left( {{\text{graphene}}} \right),$$

(4)

where $E\left( {{\text{graphene}}} \right)$ is the energy of the supercell of the initial GP containing m carbon atoms, $E\left( {{\text{SV}} - {\text{graphene}}} \right)$ is the energy of the same supercell of defective GP in which one carbon atom is removed from the cell.

The energy of the formation of a single vacancy on GP calculated using the LDA and LSDA functionals ($E_{f}^{{{\text{SV}}}} = ~$ 7.46 eV) coincide and are only slightly higher than the energy obtained using the PBE functional ($E_{f}^{{{\text{SV}}}}$ = 7.3 eV [11]; 7.7 eV [3]).

3.3 3.3. $G{{P}_{V}}\left\langle {A{{u}_{{ads}}}} \right\rangle$ Band Structure

The top of the valence state and the lower part of the conduction state in pure GP is known to de degenerate in the Dirac points (Fig. 3) of the Brillouin zone. The band structure of the 5 × 5 supercells based on a GP monolayer with an Au_ads adatom calculated by us along the highly symmetric M–Γ–K–M directions is presented in Fig. 4. The valence band of pure GP comes into contact with the neighboring energy bands with the zero band-gap energy ${{E}_{{\text{g}}}} = {{E}_{{\text{c}}}} - {{E}_{{\text{v}}}} \approx 0$ eV (E_c is the conduction band and E_v is the valence band). In the absence of impurity atoms and lattice defects, the movement of electrons within Eg is prohibited. However, the arrangement of energy bands in GP is similar to the arrangement of energy bands in semiconductors; therefore, the conduction of GP is worse than that of metals.

Fig. 3.

Hexagonal Brillouin zone of graphene. K and K' are Dirac points.

Fig. 4.

Calculated electronic band structure of a 5 × 5 supercell based on GP with an Au_ads adatom ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ along main M–Γ–K–M directions of the hexagonal Brillouin zone: (a) pure GP, (b) ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$, and (c) ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle .$ The Fermi level (${{E}_{{\text{F}}}}$) is zero. Adatom is adsorbed at the T site of GP.

Fig. 4.

(Contd.)

Figure 4a shows the electronic band structure of pure GP along the highly symmetric line of the Brillouin zone. The GP monolayer has a semiconductor band structure with a zero band-gap energy. As is seen from Fig. 4a, the valence band and the conduction band of GP join in the Dirac point (K-symmetry point) with the zero density of states.

The energy bands of the valence state and the conduction state of pure GP are characterized by linear dispersion in the vicinity of the Fermi energy in the Г point of the Brillouin zone. Such a band structure of GP (Fig. 4a) leads to a zero effective mass of electrons and holes and a high carrier mobility on the Dirac point. The band structure of the GP plane is a direct band-gap semiconductor.

The band structure of GP containing a ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ adatom is characterized by the hole nature of conduction (Fig. 4b). This is related to the fact that a monovalent Au_ads adatom is an acceptor for a tetravalent carbon atom. As a result of covalent bonding between Au–C, one electron is absent in one of the four covalent bonds which are a part of the GP lattice.

The same takes place in the ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ structure with a vacancy (Fig. 4c). An Au_ads adatom forms a covalent bond with one of the four neighboring carbon atoms. To form bonds with three other carbon atoms, a gold atom lacks a valence electron. In this case, it captures valence electrons from the covalent bond between the neighboring carbon atoms. Hence, in the ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ structure, an Au_ads adatom becomes a negatively charged ion and GP has hole conduction.

As is seen from Figs. 4b and 4c, the energy minimum of the valence band and energy maximum of the conduction band of GP structures occur at different points of the Brillouin zone; i.e., these structures are analogous to indirect-band-gap semiconductors. In the ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ structure, a band gap with an energy of ∼0.1 eV is formed. Incorporation of a vacancy into the ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ structure leads to widening of the ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ band gap.

3.4 Density of States

Figure 5 presents the total and partial spin-polarized density of states (PDOS) for gold atoms in 5 × 5 ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercells with a monovacancy. The electronic densities of states with the spin directed upward and downward are shown.

Fig. 5.

Calculated total and partial densities of states (PDOS) of 5 × 5 GP supercells for s, p, and d electrons of Au_ads: (a) DOS of a GP supercell: (1) pure GP and (2) GP with a monovacancy; (b) PDOS of a ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercell, and (c) PDOS of a ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ with a monovacancy.

Fig. 5.

(Contd.)

Fig. 5.

(Contd.)

Analysis of the total and partial spin-polarized densities of the electronic states of 5 × 5 GP supercells demonstrates that the vacancy + Au_ads adatom complex at the surface leads to a change in the DOS in the vicinity of the Fermi level. A noticeable contribution to the DOS near the Fermi level is made by the d electrons of gold.

Therefore, the arrangement of energy levels and thus the density of states depend on the GP properties (e.g., the size and concentration of vacancies) and on the contribution of the nature of the donor atom supplying a free electron.

3.5 Magnetic Moment

There are no experimental data for the magnetic properties of ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercells. For the defect-free GP supercell, the magnetic moment (m_cell (µ_B)) should be zero. Magnetism was studied by DFT assuming that there is a single vacancy of carbon in the ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercell. In this case, it was assumed that the vacancy is isolated and interaction between possible point defects in a crystal is excluded.

An increase in the number of vacancies in GP would lead to interaction between defects, which would enhance delocalization of the wave function of electrons in the region of the carbon deficiency. In other words, for the calculation, we considered a limiting case, in which one carbon atom bonded to other carbon atoms was removed from the ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercell.

The presence of a vacancy in the ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ structure leads to magnetic ordering. DFT calculations indicate that local ferromagnetic spin ordering takes place in the ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercell. In other words, the ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ system based on GP with a point defect (vacancy), similarly to other GP systems [11, 12], has a local magnetic moment.

Table 2 lists the magnetic moments for the ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ structures calculated by us.

Table 2.   DFT LSDA-calculated position of Au_ads adatom at the surface of GP (${{h}_{{\text{a}}}}$), average distance from the attached carbon atom (${{d}_{{{\text{eq}}}}}$) to Au_ads, and overall magnetization (${{m}_{{{\text{cell}}}}}$) of an Au_ads adatom adsorbed on 5 × 5 ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercells. The data are shown for the binding place of Au–C atoms, where an Au_ads adatom is located on top (T site) of the surface

Hence, ferromagnetism of the ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercell arises due to the carbon vacancy and interaction between the Au_ads adatom (4f  ¹⁴4d¹⁰4s¹) and the carbon atom. A gold atom with an unoccupied f level makes a contribution to the total ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ magnetization.

For the GP supercell with a carbon monovacancy, the calculated magnetic moment is higher than 1 ${{\mu }_{{\text{B}}}}$ (Table 2). The ${{\mu }_{{\text{B}}}}$ value for ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ is different from the values for analogous structures, e.g., ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{G}}{{e}_{{{\text{ads}}}}}} \right\rangle$ 1.77${{\mu }_{{\text{B}}}}$ [12]. The high density of states in the vicinity of the Fermi surface gives the total magnetic moment, which confirms the appearance of ferromagnetism in ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ defective GP due to the carbon vacancies.

It is established that, depending on the distance between the carbon vacancy and the Au_ads–C complex at the GP surface, the local magnetic moment can both increase (in the case of the carbon vacancy С50) and decrease (in the case of the carbon vacancy С25).

4 CONCLUSIONS

The ab initio calculations using density functional theory (DFT) in the local spin-density approximation (LSDA) for 5 × 5 ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercells and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ revealed the following information.

The position of adsorbed gold atoms on top (tetrahedral configuration, T site) of a carbon site in the surface monolayer of GP is energetically more favorable than the positions in the bridge regions between the C–C bonds (B site) and in hollows at the centers of the six-member rings of the C–C bonds (H site) of a GP cell.

The energy of formation of a carbon vacancy on GP ($E_{f}^{{{\text{SV}}}} = ~$ 7.46 eV), the band structure, and the density of states in the adsorbed ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ complexes, which are important for the electron-transport properties of GP materials, where charge carriers are localized and their movement includes a diffusion process, are calculated.

The adsorption energies ($E_{{{\text{ads}}}}^{{\text{T}}}$) of a gold atom (Au_ads) calculated in the LDA on GP supercells are relatively low, which is typical of, e.g., iron-group metals. Taking into account spin polarization allows correcting the adsorption energy of Au_ads of the mentioned grapheme structures. The value of the bond energies calculated in the LSDA with allowance for the spin correction is on average higher by 0.34 eV than the $E_{{{\text{ads}}}}^{{\text{T}}}$ value calculated by LDA.

It is shown that the energy of the Au_ads adsorption of the ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ structure is lower than that of defect-free ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$. The adsorption energy in ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ and ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ depends on the imperfection of the surface and becomes lower with a decrease in the number of defects.

Similarly to the adsorption energy, the magnetic moments (${{\mu }_{{\text{B}}}}$) calculated in the LSDA for 5 × 5 GP supercells with a monovacancy (${\text{G}}{{{\text{P}}}_{{\text{V}}}}$) and a defect-free cell with the adsorbed Au_ads atom differ from each other. Taking into account the spin-orbit interaction and splitting of the f atomic states of Au, the total calculated magnetic moment of the ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercell is 0.8 ${{\mu }_{{\text{B}}}}$. In the ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercell with a monovacancy, the Au atom also contributes to the total magnetic moment. In this case, the value of the total magnetic moment of ${\text{G}}{{{\text{P}}}_{{\text{V}}}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ rises to 1.01${{\mu }_{{\text{B}}}}$. The magnetic moment near the vacancy depends on the vacancy position at the surface. In the 5 × 5 ${\text{GP}}\left\langle {{\text{A}}{{{\text{u}}}_{{{\text{ads}}}}}} \right\rangle$ supercell, for, e.g., the С50 and С25 carbon vacancy, the partial magnetic moment is 0.83 and 0.65${{\mu }_{{\text{B}}}}$, respectively.