A Cell Model of an Ion-Exchange Membrane. Capillary-Osmosis and Reverse-Osmosis Coefficients

Abstract

The capillary-osmosis and reverse-osmosis coefficients of an ion-exchange membrane have been calculated as the kinetic coefficients of the Onsager matrix within the thermodynamics of nonequilibrium processes and on the basis of the cell model proposed previously by the author for charged porous layers. The membrane is assumed to consist of an ordered set of spherical completely porous charged particles placed into spherical shells filled with a binary electrolyte solution. Boundary value problems have been analytically solved to determine the capillary-osmosis and reverse-osmosis coefficients of such a membrane under the Kuwabara boundary condition imposed on the cell surface. The consideration has been implemented within the framework of small deviations of system parameters from their equilibrium values under the action of external fields. Different particular cases of the obtained exact analytical equations have been studied including the case of a binary symmetric electrolyte and an ideally selective membrane. It has been shown that, for the considered cell model of an ion-exchange membrane, the Onsager reciprocity theorem is violated; i.e., the found kinetic cross coefficients are unequal to each other. The violation is explained by the fact that the reciprocity theorem is valid only for systems implying the linear thermodynamics of irreversible processes, for which generalized flows are equal to zero at nonzero thermodynamic forces.

DENOTATIONS

Roman Symbols

a                       Is the particle radius

b                       Is the cell radius

d                       Is the electrical double layer thickness

$k$                      Is the Brinkman constant

${{k}_{{\text{D}}}} = {{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} k}} \right. \kern-0em} k}$   Is the Brinkman specific hydrodynamic permeability of an ion exchanger grain

$C$                      Is the electrolyte concentration

${{C}_{0}}$                    Is the equivalent concentration of an electrolyte occurring at equilibrium with a membrane

D and D₀         Are the diffusion coefficient and characteristic diffusion coefficient, respectively

$I$                       Is the flux density of mobile charges (electric current density)

$J$                       Is the diffusion flux density

j                       Is the dimensionless diffusion flux density

F₀                     Is the Faraday constant

h                       Is the membrane thickness

$m = {{{{{{\mu }}}^{{\text{i}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{i}}}}} {{{{{\mu }}}^{{\text{o}}}}}}} \right. \kern-0em} {{{{{\mu }}}^{{\text{o}}}}}}$                 Is the viscosity ratio between a liquid in a Brinkman medium the pure liquid

${{m}_{0}} = {\text{1 - }}{{{{\gamma }}}^{3}}$                  Is the membrane macroscopic porosity

L_ij                                Are the kinetic coefficients of the Onsager matrix

r                                    Is the radial coordinate

$R$                                  Is the gas constant

$T$                                  Is the absolute temperature

p                                   Is the pressure

${{p}_{0}} = RT{{C}_{0}}$              Is the characteristic osmotic pressure

${\text{Pe}} = \frac{{a{{U}_{0}}}}{{{{D}_{0}}}}$                   Is the Peclet number

${{R}_{{\text{b}}}} = \sqrt {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} k}} \right. \kern-0em} k}} = \sqrt {{{k}_{{\text{D}}}}}$ Is the Brinkman radius (width of a filtration zone in a porous medium)

${{s}^{2}} = {{{{a}^{2}}k} \mathord{\left/ {\vphantom {{{{a}^{2}}k} {{{{{\mu }}}^{{\text{i}}}}}}} \right. \kern-0em} {{{{{\mu }}}^{{\text{i}}}}}}$               Is a dimensionless parameter

${{s}_{0}}^{2} = m{{s}^{2}} = {{{{a}^{2}}} \mathord{\left/ {\vphantom {{{{a}^{2}}} {R_{{\text{b}}}^{2}}}} \right. \kern-0em} {R_{{\text{b}}}^{2}}}$  Is a dimensionless parameter

${{U}_{0}} = {{a{{p}_{0}}} \mathord{\left/ {\vphantom {{a{{p}_{0}}} {{{{{\mu }}}^{{\text{o}}}}}}} \right. \kern-0em} {{{{{\mu }}}^{{\text{o}}}}}}$   Is the characteristic filtration velocity

$U$                       Is the solvent (water) flux density;

v                         Is the velocity vector

Z_±                     Is the ion charge number (without a sign)

Greek Symbols

${{\gamma }} = {a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b}$        Is a dimensionless parameter

${{\delta }} = {d \mathord{\left/ {\vphantom {d a}} \right. \kern-0em} a}$       Is the dimensionless thickness of an electrical double layer

$\nabla$                  Is the gradient operator

ε₀ and ε         Are the dielectric constant and the relative dielectric permittivity of a medium, respectively

${{{{\mu }}}^{{\text{o}}}}$                   Is the viscosity of a pure liquid

${{{{\mu }}}^{{\text{i}}}}$                   Is the viscosity of a liquid in a Brinkman medium

μ                     Is the chemical potential

μ₀                   Is the standard chemical potential

φ                     Is the electric potential

–ρ_V                Is the volume density of the fixed charge of a porous skeleton (ion exchanger)

${{\bar {\rho }}} = \frac{{{{{{\rho }}}_{{\text{V}}}}}}{{{{F}_{0}}}}\,\,$     Is the exchange capacity of an ion exchanger grain (absolute value)

${{\sigma }} = \frac{{{{{{\rho }}}_{{\text{V}}}}}}{{{{F}_{0}}{{C}_{0}}}}$      Is the dimensionless exchange capacity

${{{{\bar {\rho }}}}_{0}} = \frac{{{{{{\mu }}}^{{\text{o}}}}{{D}_{ + }}}}{{{{k}_{{\text{D}}}}RT}}\,$ Is the characteristic exchange capacity

Φ_i                     Denotes the gradients of external forces applied to a cell and a membrane

Indices

“1”               Indicates a physical value of deviation from its equilibrium magnitude

“e”                Indicates an equilibrium value

“o”                Indicates a value that refers to the liquid shell of a cell

“i”                 Indicates a value that refers to a porous particle in a cell

̴                      Indicates a dimensionless value

“1” and “2” Indicate the left- and right-hand sides, respectively, of a membrane located in a measuring cell

m                   Indicates a value that refers to a membrane

±              Indicates a value that refers to cations/anions

INTRODUCTION

The cell method described in detail by Happel and Brenner in their well-known monograph [1] is widely and efficiently employed to study concentrated disperse systems, including membranes. A cell model of, e.g., an ion-exchange membrane implies, in particular, replacement of a real set of chaotically arranged ion exchanger grains by a periodic array of identical porous charged spheres enclosed by concentric spherical shells, which are filled with an electrolyte and form a porous layer. In the cell method, the effects of adjacent particles are taken into account by imposing specific boundary conditions on the surface of the liquid shell. It is assumed that the gradients of external forces applied to the porous layer coincide with the local gradients for the cells. The described approach is advantageous in the fact that all parameters, such as thermodynamic fluxes and forces, included in the equations for transport through the porous layer may be directly measured in experiments. In [2], a cell model of an ion-exchange membrane was formulated; a problem concerning the determination of kinetic coefficients was set and solved in the general form, and an exact algebraic expression was, for the first time, derived for hydrodynamic permeability ${{L}_{{11}}}$ of a charged membrane. The model formulated in [2] was then used to determine electroosmotic permeability ${{L}_{{12}}}$ and specific conductivity ${{L}_{{22}}}$ of a cation-exchange membrane, while, in [3], diffusion permeability ${{L}_{{33}}}$ and electrodiffusion coefficient ${{L}_{{23}}}$ were found. The proposed cell model was successfully verified using the experimental data obtained for a cast perfluorinated MF-4SC membrane and that modified with halloysite nanotubes functionalized with platinum and iron nanoparticles in aqueous HCl solutions, as well as for an extruded MF-4SC membrane and a number of 1 : 1 electrolytes (HCl, NaCl, KCl, LiCl, and CsCl). To determine the physicochemical and geometric parameters of the model, a special computational algorithm and a program were developed within the framework of the Mathematica® computing shell for the simultaneous optimization of specific conductivity and electroosmotic permeability with respect to experimental dependences.

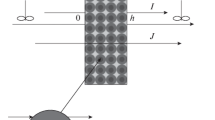
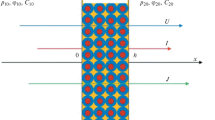
In this work, the gradients of pressure, electric potential, and chemical potential $\mu \left( C \right) = {{\mu }_{0}} + RT\ln \left( {{C \mathord{\left/ {\vphantom {C {{{C}_{0}}}}} \right. \kern-0em} {{{C}_{0}}}}} \right)$: ${{{{\Phi }_{1}} = \nabla p \approx \left( {{{p}_{{20}}} - {{p}_{{10}}}} \right)} \mathord{\left/ {\vphantom {{{{\Phi }_{1}} = \nabla p \approx \left( {{{p}_{{20}}} - {{p}_{{10}}}} \right)} h}} \right. \kern-0em} h}$, ${{{{\Phi }_{2}} = \nabla {{\varphi }} \approx \left( {{{{{\varphi }}}_{{20}}} - {{{{\varphi }}}_{{10}}}} \right)} \mathord{\left/ {\vphantom {{{{\Phi }_{2}} = \nabla {{\varphi }} \approx \left( {{{{{\varphi }}}_{{20}}} - {{{{\varphi }}}_{{10}}}} \right)} h}} \right. \kern-0em} h}$, ${{{{\Phi }_{3}} = \nabla \mu \left( C \right) \approx RT\left( {{{C}_{{20}}} - {{C}_{{10}}}} \right)} \mathord{\left/ {\vphantom {{{{\Phi }_{3}} = \nabla \mu \left( C \right) \approx RT\left( {{{C}_{{20}}} - {{C}_{{10}}}} \right)} {\left( {{{C}_{0}}h} \right)}}} \right. \kern-0em} {\left( {{{C}_{0}}h} \right)}}$, respectively, have been selected as independent thermodynamic forces, which are preset in the experiments. Here, ${{C}_{0}}$ is the equivalent concentration of an electrolyte brought in contact with a membrane, μ₀ is the standard chemical potential, h is the membrane thickness, $R$ is the gas constant, $T$ is the absolute temperature, and subscripts “1” and “2” indicate, respectively, the left- and right-hand sides of a membrane located in a measuring cell filled with a binary electrolyte solution (Fig. 1). In contrast to [2], the chemical potential gradient rather than the concentration gradient is used here to correctly derive the equations for the kinetic coefficients related to the existence of a concentration drop across the membrane, as in [3].

Fig. 1.

Membrane cell used to study nonequilibrium processes: (1, 2) donor and acceptor chambers, respectively, and (3) membrane.

Flux densities of a solvent (e.g., water), $U$; mobile charges (electric current density), $I$; and a solute (electrolyte diffusion flux density), $J$, have been taken as dependent thermodynamic parameters determined in the experiments. Then, the phenomenological transport equations for isothermal processes may be written as the following set linear equations:

$$\left\{ \begin{gathered} U = - \left( {{{L}_{{11}}}\nabla p + {{L}_{{12}}}\nabla {{\varphi }} + {{L}_{{13}}}\nabla \mu } \right), \hfill \\ I = - \left( {{{L}_{{21}}}\nabla p + {{L}_{{22}}}\nabla {{\varphi }} + {{L}_{{23}}}\nabla \mu } \right), \hfill \\ J = - \left( {{{L}_{{31}}}\nabla p + {{L}_{{32}}}\nabla {{\varphi }} + {{L}_{{33}}}\nabla \mu } \right). \hfill \\ \end{gathered} \right.$$

(1)

According to the Onsager reciprocity theorem, the matrix of kinetic coefficients must be symmetric: ${{L}_{{ik}}} = {{L}_{{ki}}}\,\,\left( {i \ne k} \right)$. However, as will be shown below, this property becomes invalid in our case. Here, we shall discuss the calculation of capillary-osmosis ${{L}_{{13}}}$ and reverse-osmosis ${{L}_{{31}}}$ coefficients of an ion-exchange membrane, with these coefficients being found by expressions that follow from Eq. (1):

$${{L}_{{13}}} = - {{\left. {\frac{U}{{\nabla {{\mu }}}}} \right|}_{{\nabla p = 0,\nabla {{\varphi }} = 0}}},$$

(2a)

$${{L}_{{31}}} = - {{\left. {\frac{J}{{\nabla p}}} \right|}_{{\nabla {{\mu }} = 0,\nabla {{\varphi }} = 0}}}.$$

(2b)

Relations (2) indicate that coefficient ${{L}_{{13}}}$ may be correctly measured only in the absence of drops of the pressure and electric potential and at preset constant chemical potential drop ${{{{\mu }}}_{{20}}} - {{{{\mu }}}_{{10}}} \approx h\nabla {{\mu }} = {\text{const}}$ across the membrane, while coefficient ${{L}_{{31}}}$ may be found in the absence of drops of the chemical and electric potentials and at preset constant pressure drop ${{p}_{{20}}} - {{p}_{{10}}} \approx h\nabla p = {\text{const}}$.

GENERAL FORMULATION OF THE PROBLEM

We shall simulate a charged membrane by a periodic array of porous spherical charged particles of the same radius $a$ enclosed by liquid spherical shells of radius $b$, which is selected in a manner such that the particle-to-cell volume ratio is equal to the volume fraction of particles in the disperse system:

$${{{{\gamma }}}^{3}} = {{\left( {{a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b}} \right)}^{3}} = 1 - {{m}_{0}},$$

(3)

where ${{m}_{0}}$ is the macroscopic porosity, which depends of the character of packing porous particles in a charged layer (membrane) (Fig. 2).

Fig. 2.

Unit cell of the membrane: (o) outer region (electrolyte solution) and (i) inner region (charged porous particle).

The mathematical formulation of the problem has been presented in [2]; here, it is not repeated for short. The denotations of the variables and parameters coincide with those in [2]. For the convenience of a reader, the list of the main denotations is presented at the beginning of the article. The flow of an incompressible liquid (electrolyte) at small Reynolds numbers (“creeping flow”) in the outer region $\left( {a < r < b} \right)$ is described by the Stokes vector differential equation supplemented with the spatial electric force. The flow of the liquid in the inner region $\left( {0 \leqslant r < a} \right)$ obeys the Brinkman vector differential equation [4], complicated by the same spatial electric force. Traditionally, a “Brinkman liquid” is assumed to be incompressible [5]. The electric potential satisfies the Poisson equation inside and outside of the particles, while the Nernst–Planck representation is used for the flux density of ions. Therewith, sources and sinks of charges are absent in the system, and the problem is considered under stationary conditions. Let, as in [2], $-{{{{\rho }}}_{{\text{V}}}}$ be the volume density of the porous skeleton fixed charge. To be more specific, the particle charge is taken to be negative (a cation-exchange membrane is simulated); then, ${{{{\rho }}}_{{\text{V}}}} > 0$. To make the analysis more convenient, we use dimensionless variables and values the same as in [2]:

$$\begin{gathered} \tilde {r} = {r \mathord{\left/ {\vphantom {r {a,\,\,\,\,{\mathbf{\tilde {v}}} = {{\mathbf{v}} \mathord{\left/ {\vphantom {{\mathbf{v}} {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}}}}} \right. \kern-0em} {a,\,\,\,\,{\mathbf{\tilde {v}}} = {{\mathbf{v}} \mathord{\left/ {\vphantom {{\mathbf{v}} {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}}}},\,\,\,\,\tilde {p} = {p \mathord{\left/ {\vphantom {p {{{p}_{0}},\,\,\,\,{{{{{\tilde {\sigma }}}}}_{{r{{\theta }}}}} = {{{{{{\sigma }}}_{{r{{\theta }}}}}} \mathord{\left/ {\vphantom {{{{{{\sigma }}}_{{r{{\theta }}}}}} {{{p}_{0}},}}} \right. \kern-0em} {{{p}_{0}},}}}}} \right. \kern-0em} {{{p}_{0}},\,\,\,\,{{{{{\tilde {\sigma }}}}}_{{r{{\theta }}}}} = {{{{{{\sigma }}}_{{r{{\theta }}}}}} \mathord{\left/ {\vphantom {{{{{{\sigma }}}_{{r{{\theta }}}}}} {{{p}_{0}},}}} \right. \kern-0em} {{{p}_{0}},}}}} \\ {{{{{\tilde {\sigma }}}}}_{{rr}}} = {{{{{{\sigma }}}_{{rr}}}} \mathord{\left/ {\vphantom {{{{{{\sigma }}}_{{rr}}}} {{{p}_{0}},}}} \right. \kern-0em} {{{p}_{0}},}}\,\,\,\,{{{\tilde {C}}}_{ \pm }}{\text{ = }}{{{{C}_{ \pm }}} \mathord{\left/ {\vphantom {{{{C}_{ \pm }}} {{{C}_{0}}}}} \right. \kern-0em} {{{C}_{0}}}}{\text{,}}\,\,\,\,{{\tilde {\varphi }}} = \frac{{{{\varphi }}{{F}_{0}}}}{{RT}}, \\ {{{\mathbf{j}}}_{ \pm }} = \frac{{{{{\mathbf{J}}}_{ \pm }}}}{{{{U}_{0}}{{C}_{0}}}},\,\,\,\,{{\nu }_{ \pm }} = {{{{D}_{0}}} \mathord{\left/ {\vphantom {{{{D}_{0}}} {{{D}_{ \pm }},}}} \right. \kern-0em} {{{D}_{ \pm }},}}\,\,\,\,{{\nu }_{{{\text{m}} \pm }}} = {{{{D}_{0}}} \mathord{\left/ {\vphantom {{{{D}_{0}}} {{{D}_{{{\text{m}} \pm }}},}}} \right. \kern-0em} {{{D}_{{{\text{m}} \pm }}},}} \\ {\text{Pe}} = \frac{{a{{U}_{0}}}}{{{{D}_{0}}}},\,\,\,\,{{\sigma }} = \frac{{{{{{\rho }}}_{{\text{V}}}}}}{{{{F}_{0}}{{C}_{0}}}},\,\,\,\,{{p}_{0}} = RT{{C}_{0}}, \\ {{U}_{0}} = {{a{{p}_{0}}} \mathord{\left/ {\vphantom {{a{{p}_{0}}} {{{{{\mu }}}^{{\text{o}}}},\,\,\,\,{{\delta }} = {d \mathord{\left/ {\vphantom {d {a,}}} \right. \kern-0em} {a,}}}}} \right. \kern-0em} {{{{{\mu }}}^{{\text{o}}}},\,\,\,\,{{\delta }} = {d \mathord{\left/ {\vphantom {d {a,}}} \right. \kern-0em} {a,}}}}\,\,\,\,m = {{{{{{\mu }}}^{{\text{i}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{i}}}}} {{{{{\mu }}}^{{\text{o}}}},}}} \right. \kern-0em} {{{{{\mu }}}^{{\text{o}}}},}} \\ {{s}^{2}} = {{{{a}^{2}}k} \mathord{\left/ {\vphantom {{{{a}^{2}}k} {{{{{\mu }}}^{{\text{i}}}},}}} \right. \kern-0em} {{{{{\mu }}}^{{\text{i}}}},}}\,\,\,\,s_{0}^{2} = m{{s}^{2}} = {{{{a}^{2}}} \mathord{\left/ {\vphantom {{{{a}^{2}}} {R_{{\text{b}}}^{2}}}} \right. \kern-0em} {R_{{\text{b}}}^{2}}}, \\ \end{gathered} $$

(4)

where ${{R}_{{\text{b}}}} = \sqrt {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} k}} \right. \kern-0em} k}}$ is the characteristic thickness of a filtration layer (Brinkman radius), ${{D}_{0}}$ is the scale of diffusion coefficients, $d = {{\left( {\frac{{{{C}_{0}}F_{0}^{2}}}{{{{\varepsilon }}{{{{\varepsilon }}}_{0}}RT}}} \right)}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ is the Debye radius, Pe is the Peclet number, and ${{F}_{0}}$ is the Faraday constant. Below, the tilde symbol will be omitted for convenience. Assuming the Debye radius to be negligibly small as compared with the particle radius, the electrical double layers (EDLs) are adequately displaced by jumps of the electric potential and ion concentrations across geometric interface $r = 1$ [2, 3]. In the absence of external forces ${{\Phi }_{i}}$ $\,\,\left( {i = 1,2,3} \right)$, each cell of the membrane is at equilibrium with an ambient quiescent electrolyte solution; i.e., the velocities and ion flux densities are equal to zero in this state. At the same time, equilibrium distributions of ions $C_{{{\text{e}} \pm }}^{{\text{o}}},\,\,C_{{{\text{e}} \pm }}^{{\text{i}}}$ and electric potential ${{\varphi }}_{{\text{e}}}^{{\text{o}}},\,\,{{\varphi }}_{{\text{e}}}^{{\text{i}}}$ are established in the system. The problem concerning the determination of the equilibrium concentrations and the potential was solved in [2] (see Eqs. (28)–(32)). Assuming that the imposition of an external field causes small deviations of the sought functions from their equilibrium values and linearizing all equations and boundary conditions of the boundary problem for the cell with respect to these small deviations (they have subscript 1), we arrive at the Laplace equations for the unknown potential and unknown nonequilibrium equivalent electrolyte concentration ${{C}_{1}} = {{Z}_{ + }}{{C}_{{1 + }}} = {{Z}_{ - }}{{C}_{{1 - }}}$ [2]:

$$\Delta {{{{\varphi }}}_{1}} = 0,\,\,\,\,\Delta {{C}_{1}} = 0.$$

(5)

These equations are valid throughout the cell.

The general solutions of Eqs. (5) were presented in [2]:

$$\begin{gathered} {{\varphi }}_{1}^{{\text{o}}} = \left( {{{G}^{{\text{o}}}}r + \frac{{{{H}^{{\text{o}}}}}}{{{{r}^{2}}}}} \right)\cos {\kern 1pt} {{\theta }},\,\,\,\,C_{1}^{{\text{o}}} = \left( {{{L}^{{\text{o}}}}r + \frac{{{{M}^{{\text{o}}}}}}{{{{r}^{2}}}}} \right)\cos {\kern 1pt} {{\theta }} \\ {\text{at }}1 < r \leqslant {1 \mathord{\left/ {\vphantom {1 {{{\gamma }}{\text{,}}}}} \right. \kern-0em} {{{\gamma }}{\text{,}}}} \\ \end{gathered} $$

(6)

$$\begin{gathered} {{\varphi }}_{1}^{{\text{i}}} = {{G}^{{\text{i}}}}r\cos {\kern 1pt} {{\theta }},\,\,\,\,C_{1}^{{\text{i}}} = {{L}^{{\text{i}}}}r\cos {\kern 1pt} {{\theta }}{\text{,}} \\ {\text{at }}0 \leqslant r < 1, \\ \end{gathered} $$

(7)

where integration constants ${{G}^{{{\text{o}}{\text{,i}}}}},\,\,{{L}^{{{\text{o}}{\text{,i}}}}},\,\,{{H}^{{\text{o}}}},\,\,{\text{and}}\,\,{{M}^{{\text{o}}}}$ are to be determined from the boundary conditions.

DETERMINATION OF CAPILLARY-OSMOSIS COEFFICIENT

Let us initially formulate the boundary conditions imposed on unit cell for this boundary value problem. The linearization of the conditions for the equality of electrochemical potentials of ions at the interface enables us to write the following [2, 3]:

$$C_{1}^{{\text{o}}} = {{{{\alpha }}}^{{\text{o}}}}\left( {{{\varphi }}_{1}^{{\text{i}}} - {{\varphi }}_{1}^{{\text{o}}}} \right),\,\,\,\,C_{1}^{{\text{i}}} = {{{{\alpha }}}^{{\text{i}}}}\left( {{{\varphi }}_{1}^{{\text{i}}} - {{\varphi }}_{1}^{{\text{o}}}} \right){\text{ at }}r = 1,$$

(8)

$$\begin{gathered} {{{{\alpha }}}^{{\text{o}}}} = \frac{{{{Z}_{ + }}{{{{\beta }}}_{ + }} + {{Z}_{ - }}{{{{\beta }}}_{ - }}}}{{{\sigma }}},\,\,\,\,{{{{\alpha }}}^{{\text{i}}}} = \frac{{{{Z}_{ + }} + {{Z}_{ - }}}}{{{\sigma }}}{{{{\beta }}}_{ + }}{{{{\beta }}}_{ - }}, \\ {{{{\beta }}}_{ \pm }} = \frac{{\exp \left( { \mp {{Z}_{ \pm }}{{\varphi }}_{{\text{e}}}^{{\text{i}}}} \right)}}{{{{{{\gamma }}}_{ \pm }}}}, \\ \end{gathered} $$

(9)

${{{{\gamma }}}_{ \pm }},\,\,\,\,{{{{\gamma }}}_{{\text{m}}}} = \sqrt {{{{{\gamma }}}_{ + }}{{{{\gamma }}}_{ - }}}$ are the coefficients of the equilibrium distributions for ions and molecules of the electrolyte in an ion exchanger grain (gel), respectively; and ${{\varphi }}_{{\text{e}}}^{{\text{i}}}$ is the equilibrium dimensionless electric potential in the grain, with this potential being found by equation ${{{{\beta }}}_{ + }} - {{{{\beta }}}_{ - }} = {{\sigma }}$ [2].

At interface $r = 1$, the conditions for equality between the radial components of ion fluxes must be fulfilled, with these conditions leading to the following set of equations relative to the unknown constants (see Eq. (43a) in [2]):

$$\begin{gathered} {\text{Pe}}{{u}_{{11}}}\left( {{{{{\beta }}}_{ + }} - 1} \right) = \frac{{{{L}^{{\text{i}}}} + {{Z}_{ + }}{{{{\beta }}}_{ + }}{{G}^{{\text{i}}}}}}{{{{\nu }_{{{\text{m}} + }}}}} \\ - \,\,\frac{{{{L}^{{\text{o}}}} - 2{{M}^{{\text{o}}}} + {{Z}_{ + }}\left( {{{G}^{{\text{o}}}} - 2{{H}^{{\text{o}}}}} \right)}}{{{{\nu }_{ + }}}}, \\ {\text{Pe}}{{u}_{{11}}}\left( {{{{{\beta }}}_{ - }} - 1} \right) = \frac{{{{L}^{{\text{i}}}} - {{Z}_{ - }}{{{{\beta }}}_{ - }}{{G}^{{\text{i}}}}}}{{{{\nu }_{{{\text{m}} - }}}}} \\ - \,\,\frac{{{{L}^{{\text{o}}}} - 2{{M}^{{\text{o}}}} - {{Z}_{ - }}\left( {{{G}^{{\text{o}}}} - 2{{H}^{{\text{o}}}}} \right)}}{{{{\nu }_{ - }}}}. \\ \end{gathered} $$

(10)

Here, taking into account the form of the general solution for radial velocity component ${{u}_{1}}$, the following denotation has been introduced:

$${{u}_{{11}}} \equiv \frac{{{{{\left. {{{u}_{1}}} \right|}}_{{r = 1}}}}}{{\cos {\kern 1pt} {{\theta }}}}.$$

(11)

Cell pressure gradient ${{\Phi }_{1}}$ was previously determined as $\nabla p = {{ - F} \mathord{\left/ {\vphantom {{ - F} V}} \right. \kern-0em} V}$, where $V = {{4{{\pi }}{{b}^{3}}} \mathord{\left/ {\vphantom {{4{{\pi }}{{b}^{3}}} 3}} \right. \kern-0em} 3}$ is the cell volume, while $F = - 4{{\pi }}Ba{{{{\mu }}}^{{\text{o}}}}{{U}_{0}}$ is the force applied from the side of a liquid to a porous charged particle [1, 2], this leading to

$${{\Phi }_{1}} = \nabla p = 3B{{{{\gamma }}}^{3}}\frac{{{{{{\mu }}}^{{\text{o}}}}{{U}_{0}}}}{{{{a}^{2}}}}.$$

(12)

Cell electric potential gradient ${{\Phi }_{2}}$ was determined in [3] as

$$\nabla {{\varphi }} = \frac{{RT}}{{a{{F}_{0}}}}\frac{{{{{\left. {{{\varphi }}_{1}^{{\text{o}}}} \right|}}_{{r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}{\text{;}{\theta }} = 0}}} - {{{\left. {{{\varphi }}_{1}^{{\text{o}}}} \right|}}_{{r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}{\text{;}{\theta }} = {{\pi }}}}}}}{{{2 \mathord{\left/ {\vphantom {2 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}}}.$$

(13)

Analogously to [3], let us introduce cell chemical potential gradient ${{\Phi }_{3}}$ as follows:

$$\nabla {{\mu }}\left( C \right) = \frac{{RT{{Z}_{0}}}}{a}\frac{{{{{\left. {C_{1}^{{\text{o}}}} \right|}}_{{r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}{\text{;}{\theta }} = 0}}} - {{{\left. {C_{1}^{{\text{o}}}} \right|}}_{{r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}{\text{;}{\theta }} = {{\pi }}}}}}}{{{2 \mathord{\left/ {\vphantom {2 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}}},$$

(14)

where ${{Z}_{0}} = {{\left( {{{Z}_{ + }} + {{Z}_{ - }}} \right)} \mathord{\left/ {\vphantom {{\left( {{{Z}_{ + }} + {{Z}_{ - }}} \right)} {{{Z}_{ + }}{{Z}_{ - }}}}} \right. \kern-0em} {{{Z}_{ + }}{{Z}_{ - }}}}$. As follows from Eq. (2a), when calculating capillary-osmosis coefficient ${{L}_{{13}}}$, the gradients of the electric potential and pressure across the membrane must be absent, while the chemical potential gradient must be constant:

$${{\Phi }_{3}} = \frac{{RT{{Z}_{0}}}}{a}{\text{cons}}{{{\text{t}}}_{3}}.$$

(15)

With allowance for Eq. (13), first condition ${{\Phi }_{2}} = 0$ nullifies the electric potential on the cell surface:

$${{\varphi }}_{1}^{{\text{o}}} = 0\,\,{\text{at}}\,\,r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}.$$

(16)

Substituting general solution (6) for the potential into Eq. (16), we obtain

$${{G}^{{\text{o}}}} = - {{{{\gamma }}}^{3}}{{H}^{{\text{o}}}}.$$

(17)

Taking into account Eq. (12), second condition ${{\Phi }_{1}} = 0$ yields $B = 0$, thus allowing us to use the set of algebraic equations (45a) and (47a), which were obtained in [2] by imposing the Kuwabara condition (absence of vorticity) on the cell surface, for determining some constants that are necessary for solving the hydrodynamic problem (see relations (23) and (24) in [2]):

$$A = B = D = E = 0,\,\,\,\,C = F = - \frac{{{{\sigma }}{{G}^{{\text{i}}}}}}{{m{{s}^{2}}}} = {{u}_{{11}}}.$$

(18)

With regard to Eq. (14), third condition (15) imposes the following boundary condition on the concentration:

$${{\left. {C_{1}^{{\text{o}}}} \right|}_{{r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}}}} = \frac{{{\text{cons}}{{{\text{t}}}_{3}}}}{{{\gamma }}}\cos {\kern 1pt} {{\theta }}{\text{,}}$$

(19)

which, being substituted into Eq. (6), leads to relation

$${{L}^{{\text{o}}}} = {\text{cons}}{{{\text{t}}}_{3}} - {{{{\gamma }}}^{3}}{{M}^{{\text{o}}}}.$$

(20)

Taking into account the pattern of solutions (6) and (7), boundary conditions (8), (17), and (19) yield two algebraic equations for the integration constants:

$$\begin{gathered} {{G}^{{\text{i}}}} = \frac{{{\text{cons}}{{{\text{t}}}_{3}}}}{{{{{{\alpha }}}^{{\text{o}}}}}} + \left( {1 - {{{{\gamma }}}^{3}}} \right)\left( {{{H}^{{\text{o}}}} + {{{{M}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{M}^{{\text{o}}}}} {{{{{\alpha }}}^{{\text{o}}}}}}} \right. \kern-0em} {{{{{\alpha }}}^{{\text{o}}}}}}} \right), \\ {{L}^{{\text{i}}}} = \frac{{{{{{\alpha }}}^{{\text{i}}}}}}{{{{{{\alpha }}}^{{\text{o}}}}}}\left( {{\text{cons}}{{{\text{t}}}_{3}} + \left( {1 - {{{{\gamma }}}^{3}}} \right){{M}^{{\text{o}}}}} \right). \\ \end{gathered} $$

(21)

Substituting Eqs. (17), (18), (20), and (21) into set (10), we find explicit expressions for constants ${{H}^{{\text{o}}}}\,{\text{and}}\,\,{{M}^{{\text{o}}}}$:

$${{H}^{{\text{o}}}} = - \frac{{3{\text{cons}}{{{\text{t}}}_{3}}}}{{{{{{\alpha }}}^{{\text{o}}}}{{\Delta }_{{\text{0}}}}}}{{h}^{{\text{o}}}},\,\,\,\,{{M}^{{\text{o}}}} = - \frac{{{\text{cons}}{{{\text{t}}}_{3}}}}{{{{{{\alpha }}}^{{\text{o}}}}{{\Delta }_{{\text{0}}}}}}{{m}^{{\text{o}}}},\,\,\,\,{\text{where}}$$

$$\begin{gathered} {{h}^{{\text{o}}}} = \frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}} + {{{{\alpha }}}^{{\text{i}}}}\left( {\frac{1}{{{{{{\nu }}}_{ - }}{{{{\nu }}}_{{{\text{m}} + }}}}} - \frac{1}{{{{\nu }_{ + }}{{\nu }_{{{\text{m}} - }}}}}} \right), \\ {{m}^{{\text{o}}}} = \left( {1 - {{{{\gamma }}}^{3}}} \right)\left( {{{\alpha }^{{\text{i}}}}\left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{{{\text{m}} - }}}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{{{\text{m + }}}}}}}} \right) - {{\alpha }^{{\text{o}}}}\left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}}} \right)} \right) \\ + \,\,\left( {2 + {{{{\gamma }}}^{3}}} \right)\left( {\frac{{{{Z}_{ - }}{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} - \frac{{{{Z}_{ + }}{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}} + {{\alpha }^{{\text{i}}}}_{{_{{}}^{{}}}}^{{_{{_{{}}^{{}}}}^{{}}}}} \right. \\ \times \,\,\left. {\left( {\frac{{{{Z}_{ + }}}}{{{{\nu }_{ + }}{{\nu }_{{{\text{m}} - }}}}} + \frac{{{{Z}_{ - }}}}{{{{\nu }_{ - }}{{\nu }_{{{\text{m}} + }}}}}} \right) - \frac{{{{\alpha }^{{\text{o}}}}}}{{{{\nu }_{ + }}{{\nu }_{ - }}}}\left( {{{Z}_{ + }} + {{Z}_{ - }}} \right)} \right), \\ \end{gathered} $$

(22)

$$\begin{gathered} {{\Delta }_{0}} = \left( {2 + {{{{\gamma }}}^{3}}} \right)\left( {1 - {{{{\gamma }}}^{3}}} \right) \\ \times \,\,\left( {\frac{1}{{{{\alpha }^{{\text{o}}}}}}\left( {\frac{{{{Z}_{ - }}{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} - \frac{{{{Z}_{ + }}{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}}} \right) + \left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}}} \right)} \right) \\ + \,\,\frac{{\left( {{{Z}_{ + }} + {{Z}_{ - }}} \right){{{\left( {2 + {{{{\gamma }}}^{3}}} \right)}}^{2}}}}{{{{\nu }_{ - }}{{\nu }_{ + }}}} + \frac{{{{{{\alpha }}}^{{\text{i}}}}}}{{{{{{\alpha }}}^{{\text{o}}}}}}\left( {1 - {{{{\gamma }}}^{3}}} \right) \\ \times \,\,\left( {\left( {1 - {{{{\gamma }}}^{3}}} \right)\left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{{{\text{m}} - }}}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{{{\text{m}} + }}}}}} \right)} \right. \\ \left. { + \,\,\left( {2 + {{{{\gamma }}}^{3}}} \right)\left( {\frac{{{{Z}_{ + }}}}{{{{\nu }_{ + }}{{\nu }_{{{\text{m}} - }}}}} + \frac{{{{Z}_{ - }}}}{{{{\nu }_{ - }}{{\nu }_{{{\text{m}} + }}}}}} \right)} \right). \\ \end{gathered} $$

(23)

The following denotations have been introduced here and below:

$$\begin{gathered} {{{{\delta }}}_{ \pm }} = \frac{{{{Z}_{ \pm }}{{{{\beta }}}_{ \pm }}}}{{{{{{\nu }}}_{{{\text{m}} \pm }}}}} \pm \frac{{{{\sigma Pe}}\left( {{{{{\beta }}}_{ \pm }} - 1} \right)}}{{m{{s}^{2}}}}{\text{,}} \\ \nu = \frac{{{{Z}_{ + }}{{\nu }_{ - }} + {{Z}_{ - }}{{\nu }_{ + }}}}{{{{\nu }_{ + }} - {{\nu }_{ - }}}},\,\,\,\,Z = \frac{{{{Z}_{ + }}}}{{{{\nu }_{ + }}}} + \frac{{{{Z}_{ - }}}}{{{{\nu }_{ - }}}}. \\ \end{gathered} $$

(24)

Capillary-osmosis coefficient ${{L}_{{13}}}$ (2a) is found as the ratio between cell filtration velocity $U$ and cell chemical potential gradient (14):

$$\begin{gathered} {{L}_{{13}}} = - \frac{U}{{{{\Phi }_{3}}}} = - \frac{{aU}}{{RT{{Z}_{0}}{\text{cons}}{{{\text{t}}}_{3}}}} \\ = - \frac{{a{{u}_{{11}}}{{U}_{0}}}}{{RT{{Z}_{0}}{\text{cons}}{{{\text{t}}}_{3}}}} = \frac{{a{{\sigma }}{{G}^{i}}{{U}_{0}}}}{{s_{0}^{2}RT{{Z}_{0}}{\text{cons}}{{{\text{t}}}_{3}}}}, \\ \end{gathered} $$

(25)

where ${{u}_{{11}}} = {U \mathord{\left/ {\vphantom {U {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}}$ is the dimensionless filtration velocity, whose value is found from relations (18), (21)–(24):

$${{u}_{{11}}} = - \frac{{\sigma {{G}^{{\text{i}}}}}}{{m{{s}^{2}}}} = - \frac{{{{\sigma }}{{{\operatorname{const} }}_{3}}}}{{m{{s}^{2}}{{\alpha }^{{\text{o}}}}}}\left( {1 - \frac{{1 - {{{{\gamma }}}^{3}}}}{{{{\Delta }_{0}}}}\left( {3{{h}^{{\text{o}}}} + \frac{{{{m}^{{\text{o}}}}}}{{{{\alpha }^{{\text{o}}}}}}} \right)} \right).$$

(26)

The following exact expression for the capillary-osmosis coefficient follows from relations (25) and (26):

$${{L}_{{13}}} = \frac{{R_{{\text{b}}}^{2}{{{{\rho }}}_{{\text{V}}}}}}{{{{{{\mu }}}^{{\text{o}}}}{{F}_{0}}{{Z}_{0}}{{\alpha }^{{\text{o}}}}}}\left( {1 - \frac{{\left( {{\text{1}} - {{{{\gamma }}}^{3}}} \right)}}{{{{{{\alpha }}}^{{\text{o}}}}{{\Delta }_{0}}}}\left( {{\text{3}}{{\alpha }^{{\text{o}}}}{{h}^{{\text{o}}}} + {{m}^{{\text{o}}}}} \right)} \right).$$

(27)

ANALYSIS OF CAPILLARY-OSMOSIS COEFFICIENT AND DISCUSSION OF RESULTS

The passage to important particular cases makes it possible to simplify exact equation (27) obtained for the capillary-osmosis coefficient. This equation is equally applicable to both a porous charged membrane and a concentrated dispersion of charged particles. This coefficient determines the osmotic transport of a solvent (water) through membrane pores. This transport develops in a membrane system under the action of an external concentration drop imposed on it. In the case of a highly concentrated dispersion of porous charged particles, expression (27) for the capillary-osmosis coefficient is essentially simplified:

$${{\left. {{{L}_{{13}}}} \right|}_{{{{\gamma }} = 1}}} = \frac{{R_{{\text{b}}}^{2}{{{{\rho }}}_{{\text{V}}}}}}{{{{{{\mu }}}^{{\text{o}}}}{{F}_{0}}{{Z}_{0}}{{\alpha }^{{\text{o}}}}}} = \frac{{R_{{\text{b}}}^{2}{{\rho }}_{{\text{V}}}^{2}}}{{{{{{\mu }}}^{{\text{o}}}}{{Z}_{0}}F_{0}^{2}\left( {{{Z}_{ + }}{{{{\beta }}}_{ + }} + {{Z}_{ - }}{{{{\beta }}}_{ - }}} \right){{C}_{0}}}}.$$

(28)

In the case of a 1:1 electrolyte and ideally selective ion exchanger grains $\left( {{{{{\gamma }}}_{{\text{m}}}} = + \infty } \right)$, expression (28) gives the following dimensional capillary-osmosis coefficient for a dispersion:

$${{\left. {{{L}_{{13}}}} \right|}_{{{{\gamma }} = 1}}} = \frac{{{{k}_{{\text{D}}}}{{{{\rho }}}_{{\text{V}}}}}}{{{\text{2}}{{{{\mu }}}^{{\text{o}}}}{{F}_{0}}}},$$

(29)

where ${{k}_{{\text{D}}}} = {{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} k}} \right. \kern-0em} k}$ is the Brinkman specific hydrodynamic permeability of an ion exchanger grain. This coefficient is independent of the electrolyte concentration.

Symmetric 1:1 Electrolyte

This is the most interesting case, because namely 1:1 electrolytes are most often used in experiments. In this case, we, from Eqs. (32a) presented in [2] and relations (9) and (24), obtain:

$$\begin{gathered} {{{{\alpha }}}^{{\text{o}}}} = \frac{{\sqrt {{{{{\sigma }}}^{2}} + {4 \mathord{\left/ {\vphantom {4 {{{\gamma }}_{{\text{m}}}^{2}}}} \right. \kern-0em} {{{\gamma }}_{{\text{m}}}^{2}}}} }}{{{\sigma }}},\,\,\,\,{{\alpha }^{{\text{i}}}} = \frac{2}{{{{\sigma \gamma }}_{{\text{m}}}^{2}}}{\text{,}} \\ \nu = \frac{{{{\nu }_{ + }} + {{\nu }_{ - }}}}{{{{\nu }_{ + }} - {{\nu }_{ - }}}},\,\,\,\,Z = \frac{1}{{{{\nu }_{ + }}}} + \frac{1}{{{{\nu }_{ - }}}}, \\ {{{{\delta }}}_{ \pm }} = \nu \frac{{{{{{\beta }}}_{ \pm }}}}{{{{{{\nu }}}_{{{\text{m}} \pm }}}}} \pm \frac{{\sigma {\text{Pe}}\left( {{{{{\beta }}}_{ \pm }} - 1} \right)}}{{m{{s}^{2}}}}{\text{,}}\,\,\,\,{{{{\beta }}}_{ \pm }} = \frac{{\sqrt {{{\sigma }^{2}} + {4 \mathord{\left/ {\vphantom {4 {{{\gamma }}_{{\text{m}}}^{2}}}} \right. \kern-0em} {{{\gamma }}_{{\text{m}}}^{2}}}} \pm \sigma }}{2}. \\ \end{gathered} $$

(30)

Substituting expressions (30) into Eq. (27) and taking into account definitions (23) and (24), we, after corresponding transformations carried out with regard to denotations (3) and (4), arrive at the following expressions:

$${{L}_{{13}}} = \frac{{{{k}_{{\text{D}}}}{{{{\rho }}}_{{\text{V}}}}}}{{{\text{2}}{{{{\mu }}}^{{\text{o}}}}{{F}_{0}}{{\alpha }^{{\text{o}}}}}}\left( {1 - \frac{{{{m}_{0}}}}{{{{\Delta }_{0}}}}\left( {\frac{{{{m}^{{\text{o}}}}}}{{{{\alpha }^{{\text{o}}}}}} + {\text{3}}{{h}^{{\text{o}}}}} \right)} \right),$$

(31)

where

$$\begin{gathered} \frac{{{{m}^{{\text{o}}}}}}{{{{\alpha }^{{\text{o}}}}}} + 3{{h}^{{\text{o}}}} = \left( {3 - {{m}_{0}}} \right) \\ \times \,\,\left[ {\frac{1}{{{{\alpha }^{{\text{o}}}}}}\left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} - \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}}} \right) + \frac{{{{{{\alpha }}}^{{\text{i}}}}}}{{{{{{\alpha }}}^{{\text{o}}}}}}\left( {\frac{1}{{{{\nu }_{ + }}{{\nu }_{{{\text{m}} - }}}}} + \frac{1}{{{{\nu }_{ - }}{{\nu }_{{{\text{m}} + }}}}}} \right) - \frac{{\text{2}}}{{{{\nu }_{ + }}{{\nu }_{ - }}}}} \right] \\ + \,\,3\left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}} + {{\alpha }^{{\text{i}}}}\left( {\frac{1}{{{{\nu }_{ - }}{{\nu }_{{{\text{m}} + }}}}} - \frac{1}{{{{\nu }_{ + }}{{\nu }_{{{\text{m}} - }}}}}} \right)} \right) \\ + \,\,{{m}_{0}}\left[ {\frac{{{{{{\alpha }}}^{{\text{i}}}}}}{{{{{{\alpha }}}^{{\text{o}}}}}}\left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{{{\text{m}} - }}}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{{{\text{m + }}}}}}}} \right) - \left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}}} \right)} \right], \\ \end{gathered} $$

(32)

$$\begin{gathered} {{\Delta }_{0}} = \left( {3 - {{m}_{0}}} \right){{m}_{0}}\left( {\frac{1}{{{{\alpha }^{{\text{o}}}}}}\left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} - \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}}} \right) + \left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}}} \right)} \right) \\ + \,\,\frac{{2{{{\left( {3 - {{m}_{0}}} \right)}}^{2}}}}{{{{\nu }_{ - }}{{\nu }_{ + }}}} + \frac{{{{\alpha }^{{\text{i}}}}}}{{{{\alpha }^{{\text{o}}}}}}{{m}_{0}} \\ \times \,\,\left( {{{m}_{0}}\left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{{{\text{m}} - }}}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{{{\text{m}} + }}}}}} \right) + \left( {3 - {{m}_{0}}} \right)\left( {\frac{1}{{{{\nu }_{ + }}{{\nu }_{{{\text{m}} - }}}}} + \frac{1}{{{{\nu }_{ - }}{{\nu }_{{{\text{m}} + }}}}}} \right)} \right). \\ \end{gathered} $$

(33)

Ideally selective membrane for pressure-driven membrane processes. In this case, we have

$$\begin{gathered} {{{{\gamma }}}_{{\text{m}}}}{\text{ = + }}\infty {\text{,}}\,\,\,\,{{{{\beta }}}_{ - }} = 0,\,\,\,\,{{{{\beta }}}_{ + }} = {{\sigma }}{\text{,}}\,\,\,\,{{{{\alpha }}}^{{\text{o}}}} = 1, \\ {{{{\alpha }}}^{{\text{i}}}} = 0,\,\,\,\,{{{{\delta }}}_{ + }} = \frac{{{\sigma }}}{{{{{{\nu }}}_{{{\text{m}} + }}}}} + \frac{{{{\sigma Pe}}\left( {{{\sigma }} - 1} \right)}}{{s_{0}^{2}}},\,\,\,\,{{{{\delta }}}_{ - }} = \frac{{{{\sigma Pe}}}}{{s_{0}^{2}}}. \\ \end{gathered} $$

(30а)

At the same time, expressions (31)–(33) are markedly simplified and yield the following dimensional expression for coefficient ${{L}_{{13}}}$:

$${{L}_{{13}}} = \frac{{3{{k}_{{\text{D}}}}{{{{\rho }}}_{{\text{V}}}}}}{{2{{{{\mu }}}^{{\text{o}}}}{{F}_{0}}}}\frac{1}{{{{m}_{0}}{{{{\delta }}}_{ + }}{{\nu }_{ + }} + \left( {3 - {{m}_{0}}} \right)}},$$

(34)

or

$${{L}_{{13}}} = \frac{{3{{k}_{{\text{D}}}}}}{{2{{{{\mu }}}^{{\text{o}}}}}}\frac{{{{\bar {\rho }}}{{C}_{0}}}}{{{{m}_{0}}{{\bar {\rho }}}\left( {\frac{{{{D}_{{{\text{m}} + }}}}}{{{{D}_{ + }}}} + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right) + \left( {3 - {{m}_{0}}\left( {1 + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right)} \right){{C}_{0}}}},$$

(35)

where it has been taken into account that ${{\sigma Pe = }}\frac{{s_{0}^{2}{{\bar {\rho }}}}}{{{{{{\nu }}}_{ + }}{{{{{\bar {\rho }}}}}_{0}}}}{\text{,}}\,\,\,\,{{\bar {\rho }}} = \frac{{{{{{\rho }}}_{{\text{V}}}}}}{{{{F}_{0}}}},$ while ${{{{\bar {\rho }}}}_{0}} = \frac{{{{{{\mu }}}^{{\text{o}}}}{{D}_{ + }}}}{{{{k}_{{\text{D}}}}RT}}$ is the characteristic scale of the exchange capacity. In the absence of macroporosity (m₀ = 0), Eq. (35) gives the following expression for the constant value of the capillary-osmosis coefficient: ${{\left. {{{L}_{{13}}}} \right|}_{{{{m}_{0}} = 0}}} = \frac{{{{k}_{{\text{D}}}}{{\bar {\rho }}}}}{{2{{{{\mu }}}^{{\text{o}}}}}}$, this expression coinciding with Eq. (29).

It is seen that expression (35) for the capillary-osmosis coefficient is directly proportional to the hydrodynamic permeability of a cation exchanger grain (gel) and inversely proportional to the solution viscosity. Note that, as follows from Eq. (35), the sign of coefficient L₁₃, is always positive at physically acceptable values of the key parameters of the system; i.e., the osmotic flux of the solvent is directed oppositely to the electrolyte concentration gradient, and the liquid penetrating through the membrane “tries” to dilute a more concentrated solution.

It should also be noted that the equation of the specific conductivity obtained previously for the case under consideration has the pattern structurally similar to Eq. (35):

$$\begin{gathered} {{L}_{{22}}} = \frac{{F_{0}^{2}{{D}_{ + }}{{C}_{0}}}}{{RT\left( {3 - {{m}_{0}}} \right)}}\left( {2{{m}_{0}}\left( {1 + \frac{{{{D}_{ - }}}}{{{{D}_{ + }}}}} \right)_{{_{{_{{}}^{{}}}}^{{_{{_{{}}^{{}}}}^{{}}}}}}^{{_{{_{{}}^{{_{{_{{}}^{{}}}}^{{}}}}}}^{{}}}}} \right. \\ + \,\,\left. {\frac{{9\left( {1 - {{m}_{0}}} \right)\left( {\frac{{{{D}_{{{\text{m}} + }}}}}{{{{D}_{ + }}}} + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right){{\bar {\rho }}}}}{{{{m}_{0}}{{\bar {\rho }}}\left( {\frac{{{{D}_{{{\text{m}} + }}}}}{{{{D}_{ + }}}} + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right) + \left( {3 - {{m}_{0}}\left( {1 + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right)} \right){{C}_{0}}}}} \right). \\ \end{gathered} $$

(36)

It follows from Eq. (35) that all curves for the capillary-osmosis coefficient of an ideally selective cation-exchange membrane have rectilinear asymptotics at low electrolyte concentrations

$${{\left. {{{L}_{{13}}}} \right|}_{{{{C}_{0}} \to 0}}} \simeq \frac{{3{{k}_{{\text{D}}}}}}{{2{{{{\mu }}}^{{\text{o}}}}}}\frac{{{{C}_{0}}}}{{{{m}_{0}}\left( {\frac{{{{D}_{{{\text{m}} + }}}}}{{{{D}_{ + }}}} + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right)}} \equiv {{b}_{0}}{{C}_{0}},\,\,\,\,{{m}_{0}} \ne 0,$$

(37)

and, at high electrolyte concentrations, they become constant:

$${{\left. {{{L}_{{13}}}} \right|}_{{{{C}_{0}} \to \infty }}} \simeq \frac{{3{{k}_{{\text{D}}}}}}{{2{{{{\mu }}}^{{\text{o}}}}}}\frac{{{{\bar {\rho }}}}}{{3 - {{m}_{0}}\left( {1 + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right)}} \equiv {{a}_{\infty }}.$$

(38)

As is seen from expressions (37) and (38), the slope of straight line (37) is always positive; i.e., ${{b}_{0}} > 0$. At the same time, ${{a}_{\infty }} > 0,$ provided that ${{{{\bar {\rho }}}} \mathord{\left/ {\vphantom {{{{\bar {\rho }}}} {{{{{{\bar {\rho }}}}}_{0}}}}} \right. \kern-0em} {{{{{{\bar {\rho }}}}}_{0}}}} < {3 \mathord{\left/ {\vphantom {3 {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}} - 1$ and ${{a}_{\infty }} < 0,\,$ if ${{{{\bar {\rho }}}} \mathord{\left/ {\vphantom {{{{\bar {\rho }}}} {{{{{{\bar {\rho }}}}}_{0}}}}} \right. \kern-0em} {{{{{{\bar {\rho }}}}}_{0}}}} > {3 \mathord{\left/ {\vphantom {3 {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}} - 1 > 2$. The latter case is not realized in practice, because ${{{{\bar {\rho }}}}_{0}} > {{\bar {\rho }}}$. Hence, for an ideally selective membrane, the ${{L}_{{13}}}\left( {{{C}_{0}}} \right)$ dependence monotonically increases from zero to an asymptotic value represented by relation (38). The nonideality of an ion exchange membrane qualitatively “deforms” the ${{L}_{{13}}}\left( {{{C}_{0}}} \right)$ dependence, and a maximum arises in it. Figure 3 shows the behavior of normalized capillary-osmosis coefficient ${{\bar {L}}_{{13}}} \equiv \left( {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} {{{k}_{{\text{D}}}}}}} \right. \kern-0em} {{{k}_{{\text{D}}}}}}} \right){{L}_{{13}}}$ calculated by exact equation (31) (curve 1, ${{{{\gamma }}}_{{\text{m}}}} = 0.527$) and approximate equation (35) (curve 2, ${{{{\gamma }}}_{{\text{m}}}} = + \infty$) for an ideally selective cation-exchange membrane at the same values of the physicochemical parameters which are characteristic of the cast perfluorinated MF-4SC cation-exchange membrane in a NaCl solution [11]: ${{D}_{{{\text{m}} + }}} = {{D}_{{{\text{m}} - }}} = 23.68$ µm²/s, ${{\bar {\rho } = 1}}{\text{.08}}$ mol/dm³, ${{{{\bar {\rho }}}}_{0}} = 2.18$ mol/dm³, and ${{m}_{0}} = 0.2$. It is seen that, at С₀ = 0.15 mol/dm³, an extreme is present in exact curve 1. This means a decrease in the osmotic permeability of the system at electrolyte concentrations above the aforementioned one probably due to a substantial (by a factor of 1.5) excess of the mobility of chlorine anions over the mobility of sodium cations. At the same time, if an ideally selective membrane with the same properties existed, no decrease in L₁₃ would be observed, and the coefficient would reach a marked positive value (curve 2). This may be explained by the fact that no flux of coions through an ideal membrane takes place.

Fig. 3.

Calculated dependences of normalized (1, 2) capillary-osmosis ${{\bar {L}}_{{13}}} = \left( {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} {{{k}_{{\text{D}}}}}}} \right. \kern-0em} {{{k}_{{\text{D}}}}}}} \right){{L}_{{13}}}$ (mol/dm³) and (3, 4) reverse-osmosis ${{\bar {L}}_{{31}}} = \left( {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} {{{k}_{{\text{D}}}}}}} \right. \kern-0em} {{{k}_{{\text{D}}}}}}} \right){{L}_{{31}}}$ (mol/dm³) coefficients on aqueous NaCl solution concentration ${{C}_{0}}$ (mol/dm³) for a cast perfluorinated MF-4SC membrane at (1, 3) ${{\gamma = 0}}{\text{.527}}$ and (2, 4) ${{\gamma = + }}\infty$: ideally selective cation-exchange membrane. See text for other parameters.

Ideal cation-exchange membrane (the case of excluded coions, ${{{{\gamma }}}_{{\text{m}}}} = 0$). In this case, the capillary-osmosis coefficient is equal to zero: ${{\left. {{{L}_{{13}}}\left( {{{C}_{0}}} \right)} \right|}_{{{{{{\gamma }}}_{{\text{m}}}}{\text{ = 0}}}}} = 0$. This is intuitively understandable, because there is no transport of coions through the membrane in this case; hence, they cannot transport solvent molecules through it in the absence of a pressure drop.

DETERMINATION OF REVERSE-OSMOSIS COEFFICIENT OF A CATION-EXCHANGE MEMBRANE AND DISCUSSION OF RESULTS

As follows from Eq. (2b), reverse-osmosis coefficient ${{L}_{{31}}}$ must be calculated in the absence of the electric and chemical potential gradients $\left( {{{\Phi }_{2}} = {{\Phi }_{3}} = 0} \right)$ and under a constant pressure gradient (${{\Phi }_{1}} = \nabla p = 3B{{{{\gamma }}}^{3}}\frac{{{{{{\mu }}}^{{\text{o}}}}{{U}_{0}}}}{{{{a}^{2}}}}$). This leads to the same boundary problem for a cell, the solution of which was found previously when calculating coefficient ${{L}_{{11}}}$ [2]. This solution can now be used to calculate coefficient ${{L}_{{31}}}$. The cell flux density of the salt is determined by the standard method [3]:

$$J = {{C}_{0}}{{U}_{0}}\frac{{{{{\left. {j_{{1r}}^{{\text{o}}}} \right|}}_{{r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}}}}}}{{\cos {\kern 1pt} {{\theta }}}},$$

(39)

where $j_{{1r}}^{{\text{o}}} = \frac{1}{{{{Z}_{0}}}}\left( {j_{{1r + }}^{{\text{o}}} + j_{{1r - }}^{{\text{o}}}} \right)$ is the radial component of the dimensionless local flux density of the salt, with this component being found on the cell surface by expressions (34a) presented for ion flux density in [2] taking into account Eqs. (6), (11), and (17), as well as relation ${{L}^{{\text{o}}}} = - {{{{\gamma }}}^{3}}{{M}^{{\text{o}}}}$, which is a consequence of condition ${{\Phi }_{3}} = 0$:

$$\begin{gathered} \frac{{{{{\left. {j_{{1r}}^{{\text{o}}}} \right|}}_{{r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}}}}}}{{\cos {\kern 1pt} {{\theta }}}} = {{u}_{{1{{\gamma }}}}} - \frac{1}{{{{Z}_{0}}{\text{Pe}}\cos {\kern 1pt} {{\theta }}}} \\ \times \,\left( {\left( {\frac{1}{{{{{{\nu }}}_{ + }}{{Z}_{ + }}}} + \frac{1}{{{{{{\nu }}}_{ - }}{{Z}_{ - }}}}} \right){{{\left. {\frac{{\partial C_{1}^{{\text{o}}}}}{{\partial r}}} \right|}}_{{r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}}}} + \left( {\frac{1}{{{{{{\nu }}}_{ + }}}} - \frac{1}{{{{{{\nu }}}_{ - }}}}} \right){{{\left. {\frac{{\partial {{\varphi }}_{1}^{{\text{o}}}}}{{\partial r}}} \right|}}_{{r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}}}}} \right) \\ = \frac{U}{{{{U}_{0}}}} + \frac{{3{{{{\gamma }}}^{3}}}}{{{{Z}_{0}}{\text{Pe}}}}\left( {\left( {\frac{1}{{{{{{\nu }}}_{ + }}{{Z}_{ + }}}} + \frac{1}{{{{{{\nu }}}_{ - }}{{Z}_{ - }}}}} \right){{M}^{{\text{o}}}} + \left( {\frac{1}{{{{{{\nu }}}_{ + }}}} - \frac{1}{{{{{{\nu }}}_{ - }}}}} \right){{H}^{{\text{o}}}}} \right). \\ \end{gathered} $$

(40)

Here, we have taken into account the expression for the radial velocity at cell boundary r = 1/γ. This expression may be found in [2]: ${{u}^{{\text{o}}}}(r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}) = {{u}_{{{\text{1}{\gamma }}}}}\cos {\kern 1pt} {{\theta }} = {{{U \mathord{\left/ {\vphantom {U U}} \right. \kern-0em} U}}_{0}}\cos {\kern 1pt} {{\theta }}$, i.e., ${{u}_{{{\text{1}{\gamma }}}}} = {{{U \mathord{\left/ {\vphantom {U U}} \right. \kern-0em} U}}_{0}}$.

When calculating the electroosmotic permeability coefficient, constants M^o and H^o were found from the conditions of equal normal components of ion fluxes at the interface:

$$\begin{gathered} {{M}^{{\text{o}}}} = \frac{{{\text{Pe}}{{u}_{{11}}}}}{{{{Z}_{ - }} + {{Z}_{ + }}}}\left( {\frac{{{{Z}_{ - }}\left( {{{{{\beta }}}_{ + }} - 1} \right){{\nu }_{{{\text{m}} + }}}}}{{\left( {1 - {{{{\gamma }}}^{3}}} \right){{{{\beta }}}_{ + }} + \left( {2 + {{{{\gamma }}}^{3}}} \right){{m}_{ + }}}}} \right. \\ + \,\,\left. {\frac{{{{Z}_{ + }}\left( {{{{{\beta }}}_{ - }} - 1} \right){{\nu }_{{{\text{m}} - }}}}}{{\left( {1 - {{{{\gamma }}}^{3}}} \right){{{{\beta }}}_{ - }} + \left( {2 + {{{{\gamma }}}^{3}}} \right){{m}_{ - }}}}} \right), \\ {{H}^{{\text{o}}}} = \frac{{{\text{Pe}}{{u}_{{11}}}}}{{{{Z}_{ - }} + {{Z}_{ + }}}}\left( {\frac{{\left( {{{{{\beta }}}_{ + }} - 1} \right){{\nu }_{{{\text{m}} + }}}}}{{\left( {1 - {{{{\gamma }}}^{3}}} \right){{{{\beta }}}_{ + }} + \left( {2 + {{{{\gamma }}}^{3}}} \right){{m}_{ + }}}}} \right. \\ - \left. {\frac{{\left( {{{{{\beta }}}_{ - }} - 1} \right){{{{\nu }}}_{{{\text{m}} - }}}}}{{\left( {1 - {{{{\gamma }}}^{3}}} \right){{{{\beta }}}_{ - }} + \left( {2 + {{{{\gamma }}}^{3}}} \right){{m}_{ - }}}}} \right). \\ \end{gathered} $$

(41)

Let us substitute Eq. (41) into Eq. (40) and take into account the expression for velocity u₁₁ at interface r = 1 (this expression was also found in [2]):

$$ - {{{{u}_{{11}}}} \mathord{\left/ {\vphantom {{{{u}_{{11}}}} B}} \right. \kern-0em} B} = {3 \mathord{\left/ {\vphantom {3 {\left( {m{{s}^{2}} + n{{\sigma Pe}}\left( {1 - {{{{\gamma }}}^{3}}} \right)} \right)}}} \right. \kern-0em} {\left( {m{{s}^{2}} + n{{\sigma Pe}}\left( {1 - {{{{\gamma }}}^{3}}} \right)} \right)}},$$

(42)

where

$$B = - \frac{{{U \mathord{\left/ {\vphantom {U {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}}}}{{f\left( {{{\gamma }};s} \right) + \frac{3}{{m{{s}^{2}} + n{{\sigma Pe}}\left( {1 - {{{{\gamma }}}^{3}}} \right)}}}},$$

(43)

$$\begin{gathered} f\left( {{{\gamma }};s} \right) \equiv 1 - \frac{{6{{\gamma }}}}{5} + \frac{{{{{{\gamma }}}^{6}}}}{5} \\ - \,\,\frac{{m{{{{\omega }}}_{3}}\left( s \right){{{\left( {1 - {{{{\gamma }}}^{3}}} \right)}}^{2}}}}{{3\left( {2{{{{\omega }}}_{1}}\left( s \right) - 4{{{{\omega }}}_{2}}\left( s \right) + m{{{{\omega }}}_{3}}\left( s \right)} \right)}}, \\ \end{gathered} $$

(44)

$$\begin{gathered} n = \frac{1}{{{{Z}_{ + }}{{{{\beta }}}_{ + }} + {{Z}_{ - }}{{{{\beta }}}_{ - }}}}\left[ {\frac{{{{{{\beta }}}_{ + }}\left( {{{{{\beta }}}_{ + }} - 1} \right){{\nu }_{{{\text{m}} + }}}}}{{\left( {1 - {{{{\gamma }}}^{3}}} \right){{{{\beta }}}_{ + }} + \left( {2 + {{{{\gamma }}}^{3}}} \right){{m}_{ + }}}}} \right. \\ \left. { - \,\,\frac{{{{{{\beta }}}_{ - }}\left( {{{{{\beta }}}_{ - }} - 1} \right){{\nu }_{{{\text{m}} - }}}}}{{\left( {1 - {{{{\gamma }}}^{3}}} \right){{{{\beta }}}_{ - }} + \left( {2 + {{{{\gamma }}}^{3}}} \right){{m}_{ - }}}}} \right],\,\,\,\,{{m}_{ \pm }} = \frac{{{{\nu }_{{{\text{m}} \pm }}}}}{{{{\nu }_{ \pm }}}}, \\ \end{gathered} $$

(45)

$$\begin{gathered} {{{{\omega }}}_{1}}(x) = 30\left( {\frac{{{\text{cosh}}{\kern 1pt} x}}{{{{x}^{4}}}} - \frac{{\sinh {\kern 1pt} x}}{{{{x}^{5}}}} - \frac{1}{{3{{x}^{2}}}}} \right), \hfill \\ {{{{\omega }}}_{2}}(x) = - \frac{{15}}{2}\left( {\frac{{{\text{cosh}}{\kern 1pt} x}}{{{{x}^{4}}}} - \frac{{\sinh {\kern 1pt} x}}{{{{x}^{5}}}}\left( {1 + {{x}^{2}}} \right) + \frac{2}{{3{{x}^{2}}}}} \right), \hfill \\ {{{{\omega }}}_{3}}(x) = - 90\left( {\frac{{{\text{cosh}}{\kern 1pt} x}}{{{{x}^{4}}}}\left( {1 + \frac{{{{x}^{2}}}}{6}} \right) - \frac{{\sinh {\kern 1pt} x}}{{{{x}^{5}}}}\left( {1 + \frac{{{{x}^{2}}}}{2}} \right)} \right). \hfill \\ \end{gathered} $$

(46)

For liquids with equal viscosities (m = 1), Eq. (44) acquires a simpler form with regard to Eq. (46):

$$\begin{gathered} {{\left. {f\left( {{{\gamma }};s} \right)} \right|}_{{m = 1}}} \equiv 1 - \frac{{6{{\gamma }}}}{5} + \frac{{{{{{\gamma }}}^{6}}}}{5} \\ - \,\,2\left( {\frac{1}{{s_{0}^{2}}} + \frac{1}{6} + \frac{1}{3}\frac{{\tanh {\kern 1pt} {{s}_{0}}}}{{\tanh {\kern 1pt} {{s}_{0}} - {{s}_{0}}}}} \right){{\left( {1 - {{{{\gamma }}}^{3}}} \right)}^{2}}. \\ \end{gathered} $$

(44a)

It may be shown that the multiplier before the term ${{\left( {1 - {{{{\gamma }}}^{3}}} \right)}^{2}}$ in expression (44a) decreases from –1/5 at s₀ = a/R_b = 0 to –1/3 at s₀ → ∞; i.e., it does not change significantly. The case of s₀ = 0 corresponds to a high permeability of a porous grain (large Brinkman radius), while s₀ → ∞ is consistent with a low permeability (small Brinkman radius). Then, identity (44a) yields:

$$\begin{gathered} {{\left. {\mathop {\lim }\limits_{s = {{s}_{0}} \to 0} f\left( {{{\gamma }};s} \right)} \right|}_{{m = 1}}} \equiv 1 - \frac{{6{{\gamma }}}}{5} + \frac{{{{{{\gamma }}}^{6}}}}{5} - \frac{1}{5}{{\left( {1 - {{{{\gamma }}}^{3}}} \right)}^{2}} \\ = \,\,\frac{4}{5} - \frac{{6{{\gamma }}}}{5} + \frac{{2{{{{\gamma }}}^{3}}}}{5} \in \left[ {0;\frac{4}{5}} \right], \\ \end{gathered} $$

(44b)

$$\begin{gathered} {{\left. {\mathop {\lim }\limits_{s = {{s}_{0}} \to \infty } f\left( {{{\gamma }};s} \right)} \right|}_{{m = 1}}} \equiv 1 - \frac{{6{{\gamma }}}}{5} + \frac{{{{{{\gamma }}}^{6}}}}{5} - \frac{1}{3}{{\left( {1 - {{{{\gamma }}}^{3}}} \right)}^{2}} \\ = \,\,\frac{2}{3} - \frac{{6{{\gamma }}}}{5} + \frac{{2{{{{\gamma }}}^{3}}}}{3} - \frac{{2{{{{\gamma }}}^{6}}}}{{15}} \in \left[ {0;\frac{2}{3}} \right]. \\ \end{gathered} $$

(44c)

Note that both functions (44b) and (44c) are monotonically decreasing. Taking into account Eqs. (39) and (12), as well as relations (42)–(46), we, from Eq. (2b), found the reverse-osmosis coefficient as

$$\begin{gathered} {{L}_{{31}}} \\ = \,\frac{{{{k}_{{\text{D}}}}{{C}_{0}}}}{{{{{{\mu }}}^{{\text{o}}}}}}\left( \begin{gathered} \frac{{m{{s}^{2}}f\left( {\sqrt[3]{{1 - {{m}_{0}}}};s} \right)}}{{3\left( {1 - {{m}_{0}}} \right)}} + \frac{1}{{1 + n\frac{{{{m}_{0}}{{\bar {\rho }}}}}{{{{{{\nu }}}_{ + }}{{{{{\bar {\rho }}}}}_{0}}}}}} \hfill \\ \times \,\,\left( {\frac{1}{{1 - {{m}_{0}}}} + \frac{3}{{{{Z}_{0}}}}\left( {\frac{{{{m}_{ + }}}}{{{{Z}_{ + }}}}\frac{{\left( {{{{{\beta }}}_{ + }} - 1} \right)}}{{{{m}_{0}}{{{{\beta }}}_{ + }} + \left( {3 - {{m}_{0}}} \right){{m}_{ + }}}} + } \right.} \right. \hfill \\ \left. {\left. { + \,\,\frac{{{{m}_{ - }}}}{{{{Z}_{ - }}}}\frac{{\left( {{{{{\beta }}}_{ - }} - 1} \right)}}{{{{m}_{0}}{{{{\beta }}}_{ - }} + \left( {3 - {{m}_{0}}} \right){{m}_{ - }}}}} \right)} \right) \hfill \\ \end{gathered} \right). \\ \end{gathered} $$

(47)

The first and second terms in Eq. (47) determine the transmembrane salt transport due to the convective water transfer and electrodiffusion of ions, respectively. When the permeability of ion exchanger grains is rather high (${{k}_{{\text{D}}}} \gg {{a}^{2}}$, i.e., s → 0), the first term in Eq. (47) may be ignored; when it is low (${{k}_{{\text{D}}}} \ll {{a}^{2}}$, i.e., s → ∞), the second term may be ignored.

In the case of zero macroporosity (${{m}_{0}}\,{\text{ = }}\,0$), Eq. (47) gives the following expression:

$${{\left. {{{L}_{{31}}}} \right|}_{{{{\gamma = }}1}}} = \frac{{{{k}_{{\text{D}}}}{{C}_{0}}}}{{{{{{\mu }}}^{{\text{o}}}}{{Z}_{0}}}}\left( {\frac{{{{{{\beta }}}_{ + }}}}{{{{Z}_{ + }}}} + \frac{{{{{{\beta }}}_{ - }}}}{{{{Z}_{ - }}}}} \right) = \frac{{{{k}_{{\text{D}}}}{{C}_{0}}}}{{{{{{\mu }}}^{{\text{o}}}}}}\left( {\frac{{{{{{\beta }}}_{ + }}{{Z}_{ - }} + {{{{\beta }}}_{ - }}{{Z}_{ + }}}}{{{{Z}_{ - }} + {{Z}_{ + }}}}} \right).$$

Let us present the expression of the capillary-osmosis coefficient under the same conditions for comparison:

$${{\left. {{{L}_{{13}}}} \right|}_{{{{\gamma }} = 1}}} = \frac{{{{k}_{{\text{D}}}}{{{{\rho }}}_{{\text{V}}}}}}{{{{{{\mu }}}^{{\text{o}}}}{{F}_{0}}{{Z}_{0}}{{{{\alpha }}}^{{\text{o}}}}}} = \frac{{{{k}_{{\text{D}}}}{{{{{\bar {\rho }}}}}^{2}}}}{{{{{{\mu }}}^{{\text{o}}}}{{Z}_{0}}\left( {{{Z}_{ + }}{{{{\beta }}}_{ + }} + {{Z}_{ - }}{{{{\beta }}}_{ - }}} \right){{C}_{0}}}}.$$

These equations are seen to be substantially different. Thus the Onsager reciprocity theorem is not fulfilled here. This fact has been confirmed by the data obtained in [6], where it was phenomenologically proven that, in the case of nonequilibrium thermodynamics, the matrix of kinetic coefficients is symmetric only in a particular case, in which the generalized thermodynamic fluxes are equal to zero, while the thermodynamic forces are unequal to zero. Note that we have revealed inequality ${{L}_{{ij}}} \ne {{L}_{{ji}}}$ for all cross coefficients calculated in terms of the cell model of an ion-exchange membrane. This question will be considered in detail in the next work of the author.

In the case of an ideally selective membrane, for pressure-driven processes (${{{{\gamma }}}_{{\text{m}}}} = + \infty$) and a 1:1 electrolyte, we have:

$$\begin{gathered} {{L}_{{31}}} \\ = \,\,\frac{{{{k}_{{\text{D}}}}{{C}_{0}}}}{{{{{{\mu }}}^{{\text{o}}}}}}\left( \begin{gathered} \frac{{m{{s}^{2}}f\left( {\sqrt[3]{{1 - {{m}_{0}}}};s} \right)}}{{3\left( {1 - {{m}_{0}}} \right)}} + \hfill \\ + \,\,\frac{1}{{1 + \frac{{\left( {{{\sigma }} - 1} \right){{{{\nu }}}_{{{\text{m}} + }}}}}{{{{m}_{0}}{{\sigma }}{{{{\nu }}}_{ + }} + \left( {3 - {{m}_{0}}} \right){{{{\nu }}}_{{{\text{m}} + }}}}}\frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}{{m}_{0}}}} \times \hfill \\ \times \,\,\left( {\frac{1}{{1 - {{m}_{0}}}} + } \right. \hfill \\ + \left. {\frac{3}{2}\left( {\frac{{\left( {{{\sigma }} - 1} \right){{{{\nu }}}_{{{\text{m}} + }}}}}{{{{m}_{0}}{{\sigma }}{{{{\nu }}}_{ + }} + \left( {3 - {{m}_{0}}} \right){{{{\nu }}}_{{{\text{m}} + }}}}} - \frac{1}{{\left( {3 - {{m}_{0}}} \right)}}} \right)} \right) \hfill \\ \end{gathered} \right). \\ \end{gathered} $$

(48)

In the case of zero macroporosity, Eq. (48) yields relation ${{\left. {{{L}_{{31}}}} \right|}_{{{{m}_{0}} = 0}}} = \frac{{{{k}_{{\text{D}}}}{{\bar {\rho }}}}}{{{\text{2}}{{{{\mu }}}^{{\text{o}}}}}}$, which coincides with expression (29). After identical transformations, expression (48) acquires the following form:

$$\begin{gathered} {{L}_{{31}}} = \frac{{{{k}_{{\text{D}}}}{{C}_{0}}}}{{{{{{\mu }}}^{{\text{o}}}}}} \\ \times \,\,\left( \begin{gathered} \frac{{m{{s}^{2}}f\left( {\sqrt[3]{{1 - {{m}_{0}}}};s} \right)}}{{3\left( {1 - {{m}_{0}}} \right)}} \hfill \\ + \,\,\frac{{{{m}_{0}}\frac{{{{D}_{{{\text{m}} + }}}}}{{{{D}_{ + }}}} + \left( {3 - {{m}_{0}}} \right)\frac{{{{C}_{0}}}}{{{{\bar {\rho }}}}}}}{{{{m}_{0}}\left( {\frac{{{{D}_{{{\text{m}} + }}}}}{{{{D}_{ + }}}} + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right) + \left( {3 - {{m}_{0}}\left( {1 + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right)} \right)\frac{{{{C}_{0}}}}{{{{\bar {\rho }}}}}}} \hfill \\ \times \,\,\left( {\frac{1}{{1 - {{m}_{0}}}} + \frac{3}{2}} \right. \hfill \\ \left. { \times \,\,\left( {\frac{{\left( {1 - \frac{{{{C}_{0}}}}{{{{\bar {\rho }}}}}} \right)}}{{{{m}_{0}}\frac{{{{D}_{{{\text{m}} + }}}}}{{{{D}_{{\text{ + }}}}}} + \left( {3 - {{m}_{0}}} \right)\frac{{{{C}_{0}}}}{{{{\bar {\rho }}}}}}} - \frac{1}{{\left( {3 - {{m}_{0}}} \right)}}} \right)} \right) \hfill \\ \end{gathered} \right). \\ \end{gathered} $$

(49)

In the case of an ideal cation-exchange membrane (the case of excluded coions, ${{\gamma }_{m}} = 0$), 1:1 electrolyte, and coinciding viscosities of liquids, m = 1, we have:

$${{L}_{{31}}} = \frac{{{{k}_{{\text{D}}}}{{C}_{0}}}}{{{{{{\mu }}}^{{\text{o}}}}}}\left( \begin{gathered} \frac{{\left( {1 - \frac{{6\sqrt[3]{{1 - {{m}_{0}}}}}}{5} + \frac{{{{{\left( {1 - {{m}_{0}}} \right)}}^{2}}}}{5}} \right)s_{0}^{2} - 2\left( {1 + \frac{{s_{0}^{2}}}{6} + \frac{1}{3}\frac{{s_{0}^{2}{\text{tanh}}{{s}_{0}}}}{{\tanh {{s}_{0}} - {{s}_{0}}}}} \right)m_{0}^{2}}}{{3\left( {1 - {{m}_{0}}} \right)}} \hfill \\ + \frac{{2{{m}_{0}} + 3\left( {1 - {{m}_{0}}} \right)\left( {\frac{{{{D}_{ + }}}}{{{{D}_{{{\text{m}} + }}}}} + \frac{{{{D}_{ - }}}}{{{{D}_{{{\text{m}} - }}}}}} \right)}}{{{{m}_{0}}\left( {1 - {{m}_{0}}} \right)\left( {2 + \left( {\frac{{{{D}_{ + }}}}{{{{D}_{{{\text{m}} + }}}}} - \frac{{{{D}_{ + }}}}{{{{D}_{{{\text{m}} - }}}}}} \right)\frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right)}} \hfill \\ \end{gathered} \right).$$

(50)

It follows from Eq. (50) that the reverse-osmosis coefficient of an ideal cation-exchange membrane is directly proportional to electrolyte concentration. Figure 3 shows variations in normalized reverse-osmosis coefficient ${{\bar {L}}_{{13}}} \equiv \left( {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} {{{k}_{{\text{D}}}}}}} \right. \kern-0em} {{{k}_{{\text{D}}}}}}} \right){{L}_{{13}}}$ of a cation-exchange membrane with a rise in the electrolyte concentration for the same of membrane–electrolyte system parameters, for which curves 1 and 2 were plotted. Curve 3 has been plotted for ${{\bar {L}}_{{13}}}$ by exact equation (47), while curve 4 has been plotted by Eq. (48) for an ideally selective membrane at m = 1 (equal viscosities) and s₀ = 0 (infinitely small size of ion exchanger grains). Figures 3a and 3b differ from each other by the ranges of variations in electrolyte concentration. As is seen in Fig. 3b, the cross coefficients do not differ significantly only at low electrolyte concentrations (below 0.1 M). At higher concentrations, marked quantitative and qualitative differences are observed between L₁₃ and L₃₁: the reverse-osmosis coefficient (curve 3) increases, while the capillary-osmosis coefficient (curve 1) decreases with a rise in electrolyte concentration. At the same time, no such substantial difference is observed between these coefficients calculated for ideally selective membranes (curves 2, 4).

Figure 4 illustrates the behavior of normalized reverse-osmosis coefficient ${{\bar {L}}_{{31}}} \equiv \left( {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} {{{k}_{{\text{D}}}}}}} \right. \kern-0em} {{{k}_{{\text{D}}}}}}} \right){{L}_{{31}}}$ with a rise in electrolyte concentration C₀ at different viscosity ratios between the liquids inside of the porous layer and inside of the liquid shell: m = 1 (Fig. 4a) and 5 (Fig. 4b). The value m = 5 corresponds to 20% porosity of the ion exchanger grain and coincides with macroporosity value m₀ = 0.2 chosen to construct the presented plots. In both figures, curves 1, 2, 3, and 4 correspond to the values of parameter ${{s}_{0}} \equiv {a \mathord{\left/ {\vphantom {a {\sqrt {{{k}_{{\text{D}}}}} }}} \right. \kern-0em} {\sqrt {{{k}_{{\text{D}}}}} }} = 0.1,\,\,\,\,1,{\text{ }}10,{\text{ and }}50$, respectively. The comparison between Figs. 4a and 4b indicates that an increase in the apparent viscosity of a Brinkman medium leads to a reduction in coefficient L₃₁, other conditions being equal. This reduction becomes stronger with an increase in parameter s₀ (a rise in the ion exchanger grain size). Therewith, the growth of the grain size leads to an increase in the reverse-osmosis permeability of the medium. Specific permeability k_D of the porous ion exchanger grain in Figs. 3 and 4 cannot be changed, because both coefficients L₁₃ and L₃₁ are normalized with respect to it. Curves 1 and 2 in Fig. 4 almost coincide with one another, while curve 3 is located close to them; hence, coefficient L₃₁ weakly depends on parameter s₀ within a range of its values from 0 to 10 and at electrolyte concentrations lower than 1 М. A further increase in this parameter by a half of an order of magnitude already leads to a marked growth of the reverse-osmosis permeability, which also grows with electrolyte concentration in all cases.

Fig. 4.

Calculated dependences of normalized reverse-osmosis coefficient ${{\bar {L}}_{{31}}} = \left( {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} {{{k}_{{\text{D}}}}}}} \right. \kern-0em} {{{k}_{{\text{D}}}}}}} \right){{L}_{{31}}}$ (mol/dm³) on aqueous NaCl solution concentration ${{C}_{0}}$ (mol/dm³) for a cast perfluorinated MF-4SC membrane at ${{\gamma = 0}}{\text{.527}}$; s₀ = (1) 0.1, (2) 1, (3) 10, and (4) 50; and m = (а) 1 and (b) 5. See text for other parameters.

Figure 5 shows the behavior of reverse-osmosis coefficient ${{\bar {L}}_{{31}}}$ with a rise in electrolyte concentration C₀ at different viscosity ratios between the liquids inside of the porous layer and inside of the liquid shell: m = 1 (Fig. 5a) and 5 (Fig. 5b) for a virtual MF-4SC membrane, as if it had an equilibrium distribution coefficient typical of reverse-osmosis membranes, ${{\gamma = 100}}$. It is clearly seen that the reverse-osmosis permeability of such a membrane is lower (other conditions being equal), and a twofold difference is reached at a NaCl concentration of 1 M. This effect is related to different signs of ion adsorption inside of the membrane matrix. In the first case (Fig. 4), the positive adsorption takes place; i.e., the ion concentration in the pores is higher than the equilibrium one. In the second case (Fig. 5) the sorption of the ions is negative; i.e., their concentration in the pores is decreased. This is quite natural, because reverse-osmosis membranes must retain a dissolved salt to a maximal extent. It is also worth noting that the difference between curves 1–3 in Fig. 5 is more substantial than that in Fig. 4.

Fig. 5.

Calculated dependences of normalized reverse-osmosis coefficient ${{\bar {L}}_{{31}}} = \left( {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} {{{k}_{{\text{D}}}}}}} \right. \kern-0em} {{{k}_{{\text{D}}}}}}} \right){{L}_{{31}}}$ (mol/dm³) on aqueous NaCl solution concentration ${{C}_{0}}$ (mol/dm³) for a virtual MF-4SC membrane at γ = 100; s₀ = (1) 0.1, (2) 1, (3) 10, and (4) 50; and m = (а) 1 and (b) 5. See text for other parameters.

Note that, as in previous works, at very low electrolyte concentrations, when the thicknesses of the outer and inner EDLs at the interfaces become comparable with the ion exchanger grain radius, the equations derived in this and previous works for the kinetic coefficients may lead to incorrect results. Here, we have ignored the EDL thicknesses to analytically solve the boundary value problem for an individual cell. This approach is quite justified for an ion-exchange membrane that operates in underlimiting regimes, when the electrolyte concentration near the interface is not extremely low. If electrodialysis is implemented in overlimiting regimes, when regions of spatial charges arise inside of diffusion layers and it is necessary to take into account the concomitant effects of electroconvection and dissociation of water molecules, the exactly formulated problem can be solved only numerically. Such models are known and have been published in, e.g., [7, 8]. It should be noted that there are other models of an ion-exchange membrane, e.g., microheterogeneous one [9, 10], which is actively developed by the researchers of the Kuban scientific school of membrane electrochemistry. The author intends to compare the microheterogeneous and cell models of an ion-exchange membrane in subsequent works.

It should also be noted that, to derive equations for the capillary-osmosis and reverse-osmosis coefficients of an anion-exchange membrane, it is necessary reverse the sign of ${{\sigma }}$ (or ${{\bar {\rho }}}$) in the equations obtained for these parameters.

CONCLUSIONS

In this work, the capillary-osmosis and reverse-osmosis coefficients of an ion-exchange membrane have been calculated in terms of thermodynamics of irreversible processes on the basis of the cell model that we developed previously for such membranes. The membrane is considered as an ordered array of porous charged spherical particles placed into spherical shells filled with a binary electrolyte solution. The consideration has been carried out within the framework of a small deviation of membrane system parameters from their equilibrium values in the presence of an external concentration field and a field of pressure. The Kuwabara boundary condition (the absence of liquid vorticity) has been imposed on the surfaces of liquid cells. The flows inside and outside of a porous particle have been described by the Brinkman equation and the Stokes equation of the “creeping flow,” respectively, taking into account the spatial electric force. Different limiting cases have been considered, in particular the cases of a symmetric 1:1 electrolyte and an ideally selective cation-exchange membrane. It has been shown that, for the considered cell model of an ion-exchange membrane, the Onsager reciprocity theorem is violated; i.e., the found kinetic cross coefficients are unequal to each other. This violation is explained by the fact that the reciprocity theorem is applicable only to nonequilibrium systems within the framework of linear thermodynamics of irreversible processes, for which the generalized fluxes are equal to zero at nonzero thermodynamic forces. The results of this study may be used not only for electrodialysis and electrofiltration through charged membranes, but also for the account of water transport in fuel cells, with this transport governing the lifetime of these devices. The developed model is applicable to any membranes carrying charges (in particular, to reverse-osmosis and nano-, ultra-, and microfiltration membranes).