Estimation of Methane Flow from the Bottom of the Kara Sea

Abstract

During the expedition of cruise 81 on R/V Akademik Mstislav Keldysh in 2020, extensive material, representing columns of bottom sediments up to 6 m deep in the Kara Sea, was selected. After the lithological description of the columns, sediment samples were taken from the different horizons for degassing of pore gases. The extracted gas samples were analyzed for the content of the main gases, such as methane (CH₄), carbon dioxide (CO₂), and light hydrocarbons. The characteristic features of changes in the CH₄ and CO₂ content with the depth of the bottom sediments at station 6879 (the Kara Sea shelf) were studied. A model of gas diffusion was constructed taking into account the biochemical reactions of methanogenesis and methane oxidation. The rate of methane formation can be estimated by the value J ≈ 3 × 10⁻¹⁰ μg s⁻¹ L⁻¹ (per liter of sediment). The coefficient of rate of methane consumption by microorganisms is K ≈ 0.5 × 10⁻¹⁰ s⁻¹. The methane flow from the bottom surface of the Kara Sea near station 6879 is q ≈ 3.47 × 10⁻¹ μL m⁻² yr⁻¹.

The question of the origin and distribution of gases in the layer of marine sediments on the Russian Arctic continental shelf is of great interest both for practical purposes of hydrocarbon exploration and for understanding the general biogeochemical processes in the shelf–sea–atmosphere system that affect the global climate [1]. Despite the abundant data on the seas in other regions, there are quite few results of studying the bottom sediments directly in the Arctic Ocean. This is related in particular to the difficulty of obtaining experimental material for in situ gas analysis and the challenging conditions of marine expeditions. This detailed analysis of the biogeochemical processes in the Kara Sea [2] is among the recent studies that can be distinguished. Work [3] examined the geology of the Kara Sea and its hydrocarbon potential, while work [4] provided a comprehensive analysis of the factors effecting gas emissions in the Laptev Sea.

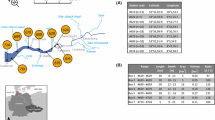
Despite the studies of organic matter (OM) and pore gases extracted from Arctic marine sediments, the processes involved in pore gas formation within marine sediments remain poorly studied. It is known that aerobic processes occur in the upper oxidized horizons of bottom sediments, while anaerobic processes take place in the lower reduced horizons where CH₄ and CO₂ are the final products of OM decomposition. The necessary experimental material was collected by the personnel from the Galimov Laboratory of Carbon Geochemistry, Institute of Geochemistry and Analytical Chemistry, Russian Academy of Sciences, during the expeditions on R/V Akademik Mstislav Keldysh (cruise 81, 2020) in the Kara Sea (Fig. 1). The present study aims to estimate the methane flow from the bottom of the Kara Sea based on the data obtained.

Fig. 1.

Stations of bottom sediment sampling during cruise 81 of R/V Akademik Mstislav Keldysh in 2020 in the Kara Sea (scale 1 : 10 000 000).

Extensive material, consisting of cores of bottom sediments up to six meters deep below the sea bottom surface, was collected [5]. After the lithological description of the columns, samples of sediments were collected from various horizons for degassing of pore gases. The extracted gas samples were analyzed for their content of major gases—methane (CH₄), carbon dioxide (CO₂), and light hydrocarbons. Later on, based on the experimental data obtained on the vertical profile of gas distribution in the marine sediment columns, a map of methane and CO₂ flow distribution from the bottom of the Kara Sea was constructed. In particular, Fig. 2 depicts the variation in CH₄ concentration with the depth of the bottom sediments at station 6879. This location was chosen for gas analysis as it is typical of the Kara Sea shelf and is far from the estuaries of the major rivers.

Fig. 2.

Distribution of methane with the depth of bottom sediments at station 6879 of the Kara Sea and model function, CH_4mod.

Depending on the geochemical conditions of the corresponding biotopes, microbial processes of sulfate reduction and methanogenesis can occur either concurrently or competitively. For instance, in the formation of CH₄ by acetate decarboxylation by acetoclastic methanogens, the processes of sulfate reduction and methanogenesis can take place concurrently. Competition arises if methanogens reduce CO₂ by hydrogen and there is a sufficient number of sulfate ions in the environment for the development of sulfate reducers and the production of hydrogen sulfide [6, 7]. In anaerobic conditions, carbon dioxide is rarely a limiting factor since it is constantly formed during fermentation reactions by the accompanying bacteria [8]. Sulfate reducers are capable of growing at lower hydrogen concentrations (dissimilatory sulfate reduction, i.e., sulfate respiration, is energetically more advantageous than methanogenesis) and using a wider range of substrates as electron donors than methanogens [9, 10]. It is known that anaerobic methane oxidation can occur through consortia of methane-oxidizing archaea from the ANME-1, -2, -3 groups and sulfate-reducing bacteria [11, 12]; however, the biochemistry of this process and the factors controlling the rate of anaerobic methane oxidation have not yet been studied sufficiently. The possibility that this process may be associated with nitrate reduction has also been demonstrated [13].

The above biochemical reactions with the involvement of microorganisms can be schematically represented as follows:

• Organoclastic sulphate reduction:

$$\begin{gathered} {\text{C}}{{{\text{H}}}_{{\text{2}}}}{\text{O}}{{({\text{N}}{{{\text{H}}}_{3}})}_{n}} + 0.5{\text{SO}}_{4}^{{2 - }} + n{\text{C}}{{{\text{O}}}_{2}} + n{{{\text{H}}}_{{\text{2}}}}{\text{O}} \\ \to \left( {1 + n} \right){\text{HCO}}_{3}^{ - } + 0.5{{{\text{H}}}_{{\text{2}}}}{\text{S}} + n{\text{NH}}_{4}^{ + }. \\ \end{gathered} $$

(1)

• Methanogenesis:

$$\begin{gathered} {\text{C}}{{{\text{H}}}_{{\text{2}}}}{\text{O}}{{({\text{N}}{{{\text{H}}}_{3}})}_{n}} + n{{{\text{H}}}^{ + }} \\ \to 0.5{\text{C}}{{{\text{O}}}_{2}} + 0.5{\text{C}}{{{\text{H}}}_{4}} + n{\text{NH}}_{4}^{ + }. \\ \end{gathered} $$

(2)

• Anaerobic oxidation of methane associated with sulfate reduction:

$${\text{C}}{{{\text{H}}}_{4}} + {\text{SO}}_{4}^{{2 - }} \to {\text{H}}{{{\text{S}}}^{ - }} + {\text{HCO}}_{3}^{ - } + {{{\text{H}}}_{{\text{2}}}}{\text{O}},$$

(3)

where n characterizes the degree of decomposition of buried organic matter (BOM).

The vertical distribution profile of gases and BOM in the sediment column can be described by the following full 1D-model, considering that there is no lateral transport.

For gases

$$\begin{gathered} \frac{{\Phi \left( x \right)\partial {{C}_{i}}\left( {x,t} \right)}}{{\partial t}} = \frac{{\partial \left[ {\Phi \left( x \right){{D}_{i}}\left( x \right)\frac{{\partial {{C}_{i}}\left( {x,t} \right)}}{{dx}}} \right]}}{{dx}} \\ - \;\frac{{\partial \left( {\Phi \left( x \right){v}\left( x \right){{C}_{i}}\left( {x,t} \right)} \right)}}{{dx}} + \Phi \left( x \right)\sum {R\left( {x,t} \right)} . \\ \end{gathered} $$

(4)

For buried organic matter (BOM),

$$\begin{gathered} \frac{{\left( {1 - \Phi \left( x \right)} \right)\partial O\left( {x,t} \right)}}{{dt}} = \frac{{\partial \left( {\left( {1 - \Phi \left( x \right)} \right)w\left( x \right)O\left( {x,t} \right)} \right)}}{{dx}} \\ + \;\left( {1 - \Phi \left( x \right)} \right)\sum {R\left( {x,t} \right)} , \\ \end{gathered} $$

(5)

where x (cm) is the depth below the bottom surface, t (yr) is the time, Φ(x) is porosity, D_i (cm² yr⁻¹) is the coefficient of diffusion of the i-component (gas) in the sediment, C_i (µM cm⁻³) is the concentration of the i-component (gas), О is the BOM concentration (dry weight, wt %) in the sediment, ${v}$ (cm yr⁻¹) is the rate of sediment accumulation, w (cm yr⁻¹) is the rate of BOM burial in the sediment, and $\sum R$ is the sum of biochemical reactions (1)–(3). In the simplest variant, at constant Φ and ${v}$, Eq. (4) for methane can be represented in the form C = C(CH₄):

$$\frac{{\partial C\left( {x,t} \right)}}{{\partial t}} = \frac{{D{{\partial }^{2}}\left( {C\left( {x,t} \right)} \right)}}{{{{\partial }^{2}}x}} - \frac{{{v}\partial \left( {C\left( {x,t} \right)} \right)}}{{\partial x}} + \frac{{dC\left( {x,t} \right)}}{{d{{t}_{{{\text{biol}}}}}}}.$$

(6)

It is commonly assumed that microbial consumption or the formation of chemical compounds in the pore water of sediments are the first-order reactions with respect to BOM that undergoes decomposition. Therefore, we offer the expression for methane consumption:

$$\frac{{dC\left( {x,t} \right)}}{{d{{t}_{{{\text{cons}}}}}}} = - KC\left( {x,t} \right),$$

(7)

where K is the coefficient of the rate of methane consumption (yr⁻¹). Under permanently steady flow conditions, methane is synthesized at a constant rate (J), determined by the balance of nutrient input and the time of doubling of the number of cells (the time of generation); i.e., we assume

$$\frac{{dC\left( {x,t} \right)}}{{d{{t}_{{{\text{prod}}}}}}} = J,~~J = {\text{const}}{\text{.}}$$

(8)

We represent the total contribution of microorganisms to the methane content in the form

$$\frac{{dC\left( {x,t} \right)}}{{d{{t}_{{{\text{biol}}}}}}} = J - KC\left( {x,t} \right).$$

(9)

The vertical distribution of methane in sediment that is steady-state and time-independent is described by the equation

$$\frac{{D{{d}^{2}}C\left( x \right)}}{{{{d}^{2}}x}} - \frac{{{v}dC\left( x \right)}}{{dx}} + J - KC\left( x \right) = 0.$$

(10)

In general form, Eq. (10) is rewritten as

$$\frac{{A{{d}^{2}}f\left( x \right)}}{{{{d}^{2}}x}} + \frac{{Bdf\left( x \right)}}{{dx}} + L + f\left( x \right) = 0,$$

(11)

where A, B, and L = const. The replacement f *(x) = L + f (x) leads (11) to have a simpler form:

$$\frac{{A{{d}^{2}}f\text{*}{\kern 1pt} \left( x \right)}}{{{{d}^{2}}x}} + \frac{{Bdf\text{*}{\kern 1pt} \left( x \right)}}{{dx}} + f\text{*}{\kern 1pt} \left( x \right) = 0.$$

(12)

The substitution f *(x) = E exp(−Rx) makes it possible to obtain the following quadratic equation for R:

$$A{{R}^{2}} - BR + 1 = 0,$$

(13)

where E = const and is determined by the boundary condition at х = 0; E = L + f(0).

If С = С₀ is the methane content at the sediment surface (x = 0) and C → C_a at x → ∞ (Fig. 2), then the solution of (10) with respect to (11)–(13) takes on the form

$$\begin{gathered} C\left( x \right) = \left( {{{C}_{0}} - \frac{J}{K}} \right)\exp \left( { - Rx} \right) + J{\text{/}}K, \\ {\text{where}}\quad R = - \frac{{v}}{{2D}} + \sqrt {{{{\left( {\frac{{v}}{{2D}}} \right)}}^{2}} + \frac{K}{D}} , \\ \end{gathered} $$

(14)

at low sedimentation rates ${v}$/D → 0, R → $\sqrt {K{\text{/}}D}$. It is known that strong currents flow to the northeast along the slope of the continental shelf in the area of sampling the column of station 6879. The sweep of sediment material is an argument in favor of the approximation made.

The value of R⁻¹, i.e., the reciprocal of $\sqrt {K{\text{/}}D}$, has the length and represents the scale (e⁻¹–interval) assigned by the ratio of diffusion and consumption of methane. This length is the depth of the sediment horizon at which the methane concentration is ≈63% (1 − e⁻¹) from the asymptotic value, C_a. If we accept that C_a = J/K ≈ 6 µg L⁻¹ for station 6879, then 1/$\sqrt {K{\text{/}}D}$ ≈ 315 cm. The estimates made for methane diffusion in the saline pore water in marine sediments [14] yield the value of D ≈ 4.6 × 10^–6 cm² s⁻¹. The coefficient of the rate of methane consumption (K) by microorganisms can be estimated as K ≈ 0.5 × 10⁻¹⁰ s⁻¹; J ≈ 3 × 10⁻¹⁰ µg s⁻¹ L⁻¹. In the 1970s–1980s, extensive geological studies of marine sediments were conducted on the coast of North America [15]. In particular, for anaerobic sediments at a depth of 200 m on the southeastern coast of the Gulf of Mexico, the value of K = 5 × 10⁻¹⁰ s⁻¹ was obtained. The coefficient of the rate of methane consumption (K) obtained in our study for bottom sediments in the Kara Sea is approximately ten times lower than in the Gulf of Mexico, which is quite reasonable in view of the significantly lower rates of organic carbon deposition and input rates in the Arctic seas, as well as the lower water and sediment temperatures.

The final model function describing the distribution of methane for station 6879 is as follows:

$$C{{\left( x \right)}_{{\bmod }}} = 6 - 5.4\exp \left( { - \frac{x}{{315}}} \right),$$

(15)

where x is the sediment depth, cm; С, µg L⁻¹.

Table 1 compares the values of С(x)_mod with the expedition measurements.

Table 1. Values of model function С(x)_mod for station 6879 of the Kara Sea

Using (16)

$$q = \frac{{DdC{{{\left( x \right)}}_{{\bmod }}}}}{{dx}},\quad x = 0,$$

(16)

we can estimate the methane flow from the seabed as q ≈ 7.9 × 10⁻¹¹ (µg cm⁻² s⁻¹) or q ≈ 3.47 × 10⁻¹ (μL m⁻² yr⁻¹). Then for the area of the Kara Sea equal to 893 400 km², the total methane flow from its seabed ≈22 t yr⁻¹.

Despite a number of simplifications, the constructed model makes it possible to describe correctly several features of methane distribution in the bottom sediments of the Kara Sea. Therefore, it is relevant to construct more detailed models of the formation and evolution of gas flows in marine sediments with the development of complex communities of microorganisms of various physiological groups.