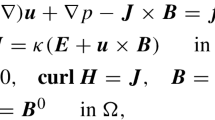Abstract
Explicit two-level in time and symmetric in space difference schemes constructed by approximating the 1D barotropic quasi-gas-/quasi-hydrodynamic systems of equations are studied. The schemes are linearized about a constant solution with a nonzero velocity, and, for them, necessary and sufficient conditions for the \({{L}^{2}}\)-dissipativity of solutions to the Cauchy problem are derived depending on the Mach number. These conditions differ from one another by at most twice. The results substantially develop the ones known for the linearized Lax–Wendroff scheme. Numerical experiments are performed to analyze the applicability of the found conditions in the nonlinear formulation to several schemes for different Mach numbers.






Similar content being viewed by others
REFERENCES
B. N. Chetverushkin, Kinetic Schemes and Quasi-Gas Dynamic System of Equations (MAKS, Moscow, 2004; CIMNE, Barcelona, 2008).
T. G. Elizarova, Quasi-Gas Dynamic Equations (Nauchnyi Mir, Moscow, 2007; Springer, Berlin, 2009).
Yu. V. Sheretov, Continuum Dynamics under Spatiotemporal Averaging (Regulyarnaya i Khaoticheskaya Dinamika, Moscow, 2009) [in Russian].
A. A. Zlotnik and B. N. Chetverushkin, “Parabolicity of the quasi-gasdynamic system of equations, its hyperbolic second-order modification, and the stability of small perturbations for them,” Comput. Math. Math. Phys. 48 (3), 420–446 (2008).
A. A. Zlotnik, “Parabolicity of a quasi-hydrodynamic system of equations and the stability of its small perturbations,” Math. Notes 83 (5), 610–623 (2008).
A. A. Zlotnik, “Energy equalities and estimates for barotropic quasi-gasdynamic and quasi-hydrodynamic systems of equations,” Comput. Math. Math. Phys. 50 (2), 310–321 (2010).
A. A. Zlotnik, “On construction of quasi-gas-dynamic systems of equations and the barotropic system with a potential body force,” Mat. Model. 24 (4), 65–79 (2012).
O. V. Bulatov and T. G. Elizarova, “Regularized shallow water equations and an efficient method for numerical simulation of shallow water flows,” Comput. Math. Math. Phys. 51 (1), 160–174 (2011).
A. Zlotnik and V. Gavrilin, “On a conservative finite-difference method for 1D shallow water flows based on regularized equations,” in Mathematical Problems in Meteorological Modeling, Mathematics in Industry, Vol. 24, Ed. by A. Bátkai, P. Csomós, A. Horányi (Springer, Cham, 2016), pp. 16–31.
V. Balashov, A. Zlotnik, and E. Savenkov, “Analysis of a regularized model for the isothermal two-component mixture with the diffuse interface,” Russ. J. Numer. Anal. Math. Model. 32 (6), 347–358 (2017).
T. G. Elizarova, A. A. Zlotnik, and M. A. Istomina, “Hydrodynamical aspects of the formation of spiral–vortical structures in rotating gaseous disks,” Astron. Rep. 62 (1), 9–18 (2018).
A. A. Sukhomozgii and Yu. V. Sheretov, “Stability analysis of a difference scheme for solving the shallow water equations,” in Applications of Functional Analysis in Approximation Theory (Tver. Gos. Univ., Tver, 2013), pp. 48–60 [in Russian].
A. Zlotnik and T. Lomonosov, “On conditions for weak conservativeness of regularized explicit finite-difference schemes for 1D barotropic gas dynamics equations,” in Differential and Difference Equations with Applications (Springer, Cham, 2018), pp. 635–647. https://arxiv.org/abs/1803.09899.
S. K. Godunov and V. S. Ryaben’kii, Difference Schemes: An Introduction to the Underlying Theory (Nauka, Moscow, 1977; North-Holland, Amsterdam, 1987).
R. D. Richtmyer and K. W. Morton, Difference Methods for Initial-Value Problems (Wiley, New York, 1967).
A. A. Zlotnik and T. A. Lomonosov, “On conditions for \({{L}^{2}}\)-dissipativity of linearized explicit QGD finite-difference schemes for one-dimensional gas dynamics equations,” Dokl. Math. 98 (2), 458–463 (2018).
A. A. Zlotnik, “Spatial discretization of the one-dimensional barotropic quasi-gasdynamic system of equations and the energy balance equation,” Mat. Model. 24 (10), 51–64 (2012).
A. A. Zlotnik, “On conservative spatial discretizations of the barotropic quasi-gasdynamic system of equations with a potential body force,” Comput. Math. Math. Phys. 56 (2), 303–319 (2016).
ACKNOWLEDGMENTS
This work was supported by the Russian Foundation for Basic Research, project nos. 19-01-00262 and 18-01-00587.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Translated by I. Ruzanova
Rights and permissions
About this article
Cite this article
Zlotnik, A.A., Lomonosov, T.A. Conditions for L2-Dissipativity of Linearized Explicit Difference Schemes with Regularization for 1D Barotropic Gas Dynamics Equations. Comput. Math. and Math. Phys. 59, 452–464 (2019). https://doi.org/10.1134/S0965542519030151
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0965542519030151