Skip to main content
SpringerLink
Log in

A theoretical measure technique for determining 3D symmetric nearly optimal shapes with a given center of mass

  • Published:
Computational Mathematics and Mathematical Physics Aims and scope Submit manuscript

Abstract

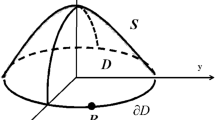
In this paper, a new approach is proposed for designing the nearly-optimal three dimensional symmetric shapes with desired physical center of mass. Herein, the main goal is to find such a shape whose image in (r, θ)-plane is a divided region into a fixed and variable part. The nearly optimal shape is characterized in two stages. Firstly, for each given domain, the nearly optimal surface is determined by changing the problem into a measure-theoretical one, replacing this with an equivalent infinite dimensional linear programming problem and approximating schemes; then, a suitable function that offers the optimal value of the objective function for any admissible given domain is defined. In the second stage, by applying a standard optimization method, the global minimizer surface and its related domain will be obtained whose smoothness is considered by applying outlier detection and smooth fitting methods. Finally, numerical examples are presented and the results are compared to show the advantages of the proposed approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. R. Butt, “Optimal shape design for differential inequalities,” PhD Thesis in Mathematics (University of Leeds, Leeds, 1988).

    MATH  Google Scholar 

  2. J. Haslinger and P. Neittaanmaki, Finite Element Approximation for Optimal Shape Design: Theory and Application (Wiley, New York, 1988).

    MATH  Google Scholar 

  3. O. Pironneau, “On optimal design in fluid mechanics,” J. Fluid Mech. 64, 97–110 (1974).

    Article  MathSciNet  MATH  Google Scholar 

  4. O. Pironneau, Optimal Shape Design for Elliptic Systems (Springer-Verlag, New York, 1983).

    MATH  Google Scholar 

  5. R. W. Ferguson, “Modeling orientation effects in symmetry detection: The role of visual structure,” Proceedings of the 22nd Annual Conference of the Cognitive Science Society (Inst. Res. Cognitive Sci. Univ. of Pennsylvania, Philadelphia, 2000), pp. 125–130.

    Google Scholar 

  6. D. Reisfeld, H. Wolfson, and Y. Yeshurun, “Context-free attentional operators: The generalized symmetry transform,” Int. J. Comput. Vision 14, (2) 119–130 (1995).

    Article  Google Scholar 

  7. H. Zabrodsky, S. Peleg, and D. Avnir, “Completion of occluded shapes using symmetry,” Computer Society Conference on Computer Vision and Pattern Recognition (1993), pp. 678–679.

    Google Scholar 

  8. M. Kazhdan, B. Chazelle, D. Dobkin, T. Funkhouser, and S. Rusinkiewicz, “A reflective symmetry descriptor for 3D models,” Algorithmica, 38 (1), 201–225 (2004).

    Article  MathSciNet  MATH  Google Scholar 

  9. P. M. Van, Space Tourism: Adventures in Earth Orbit and Beyond (Springer, New York, 2005).

    Google Scholar 

  10. D. I. Capuzzo, and H. Ishii, “Approximate solution of the Bellman equation of deterministic control theory,” Appl. Math. Optim. 102, 161–181 (1984).

    MathSciNet  Google Scholar 

  11. R. J. DiPerna, “Convergence of approximate solutions to conservation laws,” Arch. Ration. Mech. 82, 27–70 (1983).

    Article  MathSciNet  MATH  Google Scholar 

  12. M. Stefan, Variational Models for Microstructure and Phase Transitions (Lecture at the C.I.M.E. summer school Calculus of variations and geometric evolution problems, 1998).

    Google Scholar 

  13. L. Tartar, “Compensated compactness and applications to partial differential equations,” Nonlinear Anal. Mech: Heriot Watt Symp. 39, 136–212 (1979).

    MathSciNet  MATH  Google Scholar 

  14. M. Chipot and D. Kinderlehrer, “Equilibrium configurations of crystals,” Arch. Ration. Mech. 103, 237–277 (1988).

    Article  MathSciNet  MATH  Google Scholar 

  15. I. Fonseca, “Variational methods for elastic crystals,” Arch Ration. Mech. 97, 189–220 (1987).

    Article  MathSciNet  MATH  Google Scholar 

  16. E. Bonnetier and C. Conca, “Approximation of Young measures by functions and application to a problem of optimal design for plates with variable thickness,” Proc. R. Soc. Edinburgh, Sect. A 124, 399–422 (1994).

    Article  MathSciNet  MATH  Google Scholar 

  17. F. Maestre and P. Pedregal, “Quasiconvexification in 3D for a variational reformulation of an optimal design problem in conductivity,” Nonlinear Anal. 64, 1962–1976 (2006).

    Article  MathSciNet  MATH  Google Scholar 

  18. P. Pedregal, “Vector variational problems and applications to optimal design,” ESAIM Control Optim. Calc. Var. 11, 357–381 (2005).

    Article  MathSciNet  MATH  Google Scholar 

  19. J. E. Rubio, Control and Optimization: The Linear Treatment of Nonlinear Problems (Manchester Univ. Press, Manchester, 1986).

    MATH  Google Scholar 

  20. A. V. Kamyad, J. E. Rubio, and D. A. Wilson, “Optimal control of the multidimensional diffusion equation,” J. Optim. Theory Appl. 70, 191–209 (1991).

    Article  MathSciNet  MATH  Google Scholar 

  21. J. E. Rubio, “The global control of nonlinear elliptic equation,” J. Franklin Inst. 330 (1) 29–35 (1993).

    Article  MathSciNet  MATH  Google Scholar 

  22. A. Fakharzadeh, J., and J. E. Rubio, “Best domain for an elliptic problem in Cartesian coordinates by means of shape-measure,” Asian J. Control. 11, 536–554 (2009).

    Article  MathSciNet  Google Scholar 

  23. A. Fakharzadeh and J. E. Rubio, “Global solution of optimal shape design problems,” Z. Anal. Anwendungen 18, 143–155 (1999).

    Article  MathSciNet  MATH  Google Scholar 

  24. A. Fakharzadeh, J. and J. E. Rubio, “Shapes and measures,” IMA J. Math. Control Inf. 16, 207–220 (1999).

    Article  MathSciNet  MATH  Google Scholar 

  25. M. H. Mehneh, M. H. Farahi, and J. A. Eefahani, “On an optimal shape design problem to control a thermoelastic deformation under a prescribed thermal treatment,” Appl. Math. Model. 31, 663–675 (2007).

    Article  Google Scholar 

  26. A. Fakharzadeh, J. and J. E. Rubio, “Shape-measure method for solving elliptic optimal shape problems (fixed control case),” Bull. Iran. Math. Soc. 27, 41–63 (2001).

    MathSciNet  MATH  Google Scholar 

  27. A. Fakharzadeh, “A shape-measure method for solving free-boundary elliptic systems with boundary control function,” Iran. J. Numer. Anal. Optim. 3 (2), 47–65 (2013).

    Google Scholar 

  28. B. Mohammadi and O. Pironneau, Applied Shape Optimization for Fluids, 2nd ed. (Oxford Science, Oxford, 2010).

    MATH  Google Scholar 

  29. M. Andreodi, A. Janka, and J.-A. Desideri, “Free-form deformation parametrization for multi-level 3D shape optimization in aerodynamics,” Research Report (Inst. National de Recherch en Information et en Automatique, 2003).

    Google Scholar 

  30. G. Allalrf and F. Jouv, “A level-set method for variation and multiple loads structural optimization,” Comput. Methods Appl. Mech. Eng. 194, 3269–3290 (2005).

    Article  Google Scholar 

  31. B. George, R. Thomas, L. Finney, D. Maurice, and G. Weir, Calculus and Analytic Geometry (Wiley, New York, 2001).

    Google Scholar 

  32. A. Fakharzadeh, J. and Z. Rafei, “Best minimizing algorithm for shape-measure method,” J. Math. Comput. Sci. 5, 176–184 (2012).

    Google Scholar 

  33. M. Alan, Electromagnetic Field: Sources and Media (Wiley, New York, 1978).

    Google Scholar 

  34. A. Fakharzadeh, J., “Finding the optimum domain of a nonlinear wave optimal control system by measures,” J. Appl. Math. Comput. 13, 183–194 (2003).

    Article  MathSciNet  MATH  Google Scholar 

  35. M. H. Farahi, A. H. Borzabadi, H. H. Mehne, and A. V. Kamyad, “Measure theoretical approach for optimal shape design of a nozzle,” J. Appl. Math. Comput. 17, 315–328 (2005).

    Article  MathSciNet  MATH  Google Scholar 

  36. H. L. Royden, Real Analysis, 3rd ed. (Macmillan, New York, 1988).

    MATH  Google Scholar 

  37. P. C. Rosenbloom, “Qudques classes de problems exteremaux,” Bull. Soc. Math. France 80, 183–216 (1952).

    Article  Google Scholar 

  38. J. Nocedal and S. J. Wright, Numerical Optimization (Springer, New York, 2006).

    MATH  Google Scholar 

  39. H. A. Abbas, “Marriage in honey bees optimization (MBO): A haplometrosis polygynous swarming approach,” Congress on Evolutionary Computation (Seoul, Korea, 2001), pp. 207–214.

    Google Scholar 

  40. H. P. Kriegel, P. Kröger, E. Schubert, and A. Zimek, “LoOP: local outlier probabilities,” Proceedings of the 18th ACM Conference on Information and Knowledge Management, Hong Kong, China, November 2–6, 2009 (ACM, New York, 2009), pp. 1649–1652.

    Google Scholar 

  41. V. Barnett and T. Lewis, Outlier in Statistical Data (Wiley, New York, 1994).

    MATH  Google Scholar 

  42. D. Hawkins, Identification of Outliers (Chapman and Hall, London, 1980).

    Book  MATH  Google Scholar 

  43. H. P. Kriegel, P. Kröger, and A. Zimek, Outlier Detection Techniques (Tutorial Notes) (KDD, Washington, DC, 2010).

    Google Scholar 

  44. MATH2071: LAB # 5: Norms, Errors, and Condition Numbers, Retrieved from http://www.math.pitt.edu/sussmanm/ 2071Spring08/lab05/, October 6, 2014.

  45. D. R. Smith, Variational Methods in Optimization (Prentice-Hall, Englewood Cliffs, N.J, 1974).

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Shiraz University of Technology, Shiraz, Iran

    H. Alimorad D. & A. Fakharzadeh J.

Authors
  1. H. Alimorad D.
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Fakharzadeh J.
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Fakharzadeh J..

Additional information

The article is published in the original.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Alimorad D., H., Fakharzadeh J., A. A theoretical measure technique for determining 3D symmetric nearly optimal shapes with a given center of mass. Comput. Math. and Math. Phys. 57, 1225–1240 (2017). https://doi.org/10.1134/S0965542517070028

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0965542517070028

Keywords

Search

Navigation