Skip to main content
SpringerLink
Log in

Numerical simulation of the transition to chaos in a dissipative Duffing oscillator with two-frequency excitation

  • Published:
Computational Mathematics and Mathematical Physics Aims and scope Submit manuscript

Abstract

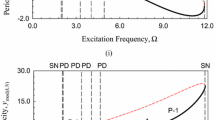
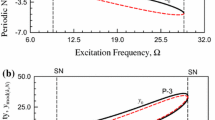
A mathematical modeling technique is proposed for oscillation chaotization in an essentially nonlinear dissipative Duffing oscillator with two-frequency excitation on an invariant torus in ℝ2. The technique is based on the joint application of the parameter continuation method, Floquet stability criteria, bifurcation theory, and the Everhart high-accuracy numerical integration method. This approach is used for the numerical construction of subharmonic solutions in the case when the oscillator passes to chaos through a sequence of period-multiplying bifurcations. The value of a universal constant obtained earlier by the author while investigating oscillation chaotization in dissipative oscillators with single-frequency periodic excitation is confirmed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. V. S. Anishchenko, Complex Oscillations in Simple Systems: Mechanisms of Formation, Structure, and Properties of Dynamic Chaos in Radiophysical Systems (Nauka, Moscow, 1990) [in Russian].

    Google Scholar 

  2. V. I. Gulyaev, T. V. Zavrazhina, and N. M. Zavrazhina, Universal Laws of Origin of Chaotic Motions in Nonlinear Mechanical Systems (VIPOL, Kiev, 1999) [in Russian].

    Google Scholar 

  3. F. C. Moon, Chaotic Vibrations (Mir, Moscow, 1990; Wiley, New York, 2004).

    MATH  Google Scholar 

  4. Yu. I. Neimark and P. S. Landa, Stochastic and Chaotic Oscillations (Nauka, Moscow, 1987; Kluwer, Dordrecht, 1992).

    Google Scholar 

  5. K. Huseyin, and R. Lin, “An Intrinsic Multiple-Scale Harmonic Balance Method for Nonlinear Vibration and Bifurcation Problems,” Int. J. Nonlinear Mech. 26, 727–740 (1991).

    Article  MATH  MathSciNet  Google Scholar 

  6. Q. Pei and L. Li, “The Chaotic Behavior of a Nonlinear Oscillator,” Appl. Math. Mech. 14, 377–387 (1993).

    MathSciNet  Google Scholar 

  7. R. Van Doorin, “On the Transition from Regular to Chaotic Behavior in the Duffing Oscillator,” J. Sound Vibration 123(2), 327–339 (1988).

    Article  MathSciNet  Google Scholar 

  8. K. Yagasaki, M. Sakata, and K. Kimura, “Dynamics of a Weakly Nonlinear System Subjected to Combined Parametric and External Excitation,” Trans. ASME J. Appl. Mech. 57(1), 209–217 (1990).

    Article  MATH  MathSciNet  Google Scholar 

  9. A. B. Belogorodtsev, “Theory of Regular and Chaotic Behavior of Weakly Nonlinear Oscillators with Quasi-Periodic Forcing,” Abstract of Papers of 2nd All-Union Conference on Nonlinear Oscillations of Mechanical Systems (Gorky, 1990), pp. 30–31.

  10. J. Brindley, “Noisy Periodicity and Nonchaotic Strange Attractors in Forced Nonlinear Oscillators,” Tagunsber Math. Forschungsinst. Oberwolfach. No. 42, 5 (1991).

  11. J. Wojewoda and T. Kapitaniak, “Oscillations of a Quasiperiodicially Forced System with Dry Friction,” J. Sound Vibration 163, 379–384 (1993).

    Article  MATH  Google Scholar 

  12. K. Yagasaki, “The Influence of Phase Locking on Chaotic Behavior in a Two-Frequency Perturbation of Duffing’s Equation, Mem. Fac. Eng. Tamagava Univ., No. 26, 15–21 (1991).

  13. Yu. N. Bibikov, Multifrequency Nonlinear Oscillations and Their Bifurcations (Leningr. Gos. Univ., Leningrad, 1991) [in Russian].

    MATH  Google Scholar 

  14. A. M. Samoilenko, Elements of the Mathematical Theory of Multifrequency Oscillations (Nauka, Moscow, 1987; Kluwer Academic, Dordrecht, 1991).

    Google Scholar 

  15. V. I. Arnol’d, Ordinary Differential Equations (Nauka, Moscow, 1971; MIT Press, Cambridge, Mass., 1973).

    Google Scholar 

  16. B. P. Demidovich, Lectures on Stability Theory (Nauka, Moscow, 1967) [in Russian].

    MATH  Google Scholar 

  17. G. Iooss and D. D. Joseph, Elementary Stability and Bifurcation Theory (Springer-Verlag, New York, 1980; Mir, Moscow, 1983).

    MATH  Google Scholar 

  18. V. I. Gulyaev, V. A. Bazhenov, E. A. Gotsulyak, et al., Stability of Periodic Processes in Nonlinear Mechanical Systems (Vishcha Shkola, Lviv, 1983) [in Russian].

    Google Scholar 

  19. M. M. Vainberg and V. A. Trenogin, Theory of Branching of Solutions of Nonlinear Equations (Nauka, Moscow, 1969; Noordhoff, Leyden, 1974).

    MATH  Google Scholar 

  20. A. Poincaré, Selected Works (Nauka, Moscow, 1971), Vols. 1–3 [in Russian].

    Google Scholar 

  21. M. J. Feigenbaum, “Universal Behavior in Nonlinear Systems,” Los Alamos Sci. 1(1), 4–27 (1980).

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. International Research and Educational Center for Information Technologies and Systems, National Academy of Sciences of Ukraine, pr. Akademika Glushkova 40, Kiev, 03680, Ukraine

    T. V. Zavrazhina

Authors
  1. T. V. Zavrazhina
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to T. V. Zavrazhina.

Additional information

Original Russian Text © T.V. Zavrazhina, 2007, published in Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki, 2007, Vol. 47, No. 10, pp. 1692–1700.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zavrazhina, T.V. Numerical simulation of the transition to chaos in a dissipative Duffing oscillator with two-frequency excitation. Comput. Math. and Math. Phys. 47, 1622–1630 (2007). https://doi.org/10.1134/S0965542507100041

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0965542507100041

Keywords

Search

Navigation