Skip to main content
SpringerLink
Log in

Bifurcation trees of period-1 motions in a periodically excited, softening Duffing oscillator with time-delay

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

A Correction to this article was published on 07 June 2019

This article has been updated

Abstract

In this paper, bifurcation trees of period-1 motions to chaos in a periodically excited, time-delay, softening Duffing oscillator are analytically predicted through an implicit mapping method. Discretization of the time-delay oscillator gives an implicit mapping. Stable and unstable periodic motions in such a time-delay, softening Duffing oscillator are achieved through the corresponding mapping structures. From the finite discrete Fourier series, harmonic frequency–amplitude characteristics for stable and unstable solutions of period-1 to period-4 motions are developed, and the singularity, catastrophes and quantity levels of harmonic amplitudes are presented. A symmetric period-1 motion with symmetric break generates three branches of period-1 motions to chaos. From the analytical prediction, periodic motions in the time-delay softening Duffing oscillator are simulated numerically. The bifurcation trees of period-1 motions to chaos in the time-delay softening Duffing oscillator are difficult to be obtained from the traditional analytical methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Change history

  • 07 June 2019

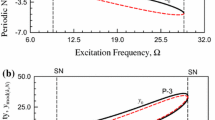
    In the original publication, Fig. 1a, b was published incorrectly. The corrected figure is given below.

References

  1. Duffing G (1918) Erzwunge Schweingungen bei veranderlicher eigenfrequenz. F. Viewig u. Sohn, Braunschweig

    MATH  Google Scholar 

  2. Hayashi C (1964) Nonlinear oscillations in physical systems. McGraw-Hill Book Company, New York

    MATH  Google Scholar 

  3. Nayfeh AH (1973) Perturbation methods. John Wiley, New York

    MATH  Google Scholar 

  4. Holmes PJ, Rand DA (1976) Bifurcations of Duffing equation: an application of catastrophe theory. Q Appl Math 35:495–509

    Article  Google Scholar 

  5. Nayfeh AH, Mook DT (1979) Nonlinear oscillation. John Wiley, New York

    MATH  Google Scholar 

  6. Holmes PJ (1979) A nonlinear oscillator with strange attractor. Philos Trans R Soc A 292:419–448

    Article  MathSciNet  MATH  Google Scholar 

  7. Ueda Y (1980) Explosion of strange attractors exhibited by the Duffing equations. Annu N Y Acad Sci 357:422–434

    Article  Google Scholar 

  8. Coppola VT, Rand RH (1990) Averaging using elliptic functions: approximation of limit cycle. Acta Mech 81:125–142

    Article  MathSciNet  MATH  Google Scholar 

  9. Roy T, Choudhury R, Tanriver U (2017) Analytical prediction of homoclinic bifurcations following a supercritical Hopf bifurcation. Discontinuity Nonlinearity Complex 6(2):209–222

    MATH  Google Scholar 

  10. Maaita JO (2016) A theorem on the bifurcations of the slow invariant manifold of a system of two linear oscillators coupled to a k-order nonlinear oscillator. J Appl Nonlinear Dyn 5(2):193–197

    Article  MathSciNet  MATH  Google Scholar 

  11. Yamgoué SB, Nana B, Pelap FB (2017) Approximate analytical solutions of a nonlinear oscillator equation modeling a constrained mechanical system. J Appl Nonlinear Dyn 6(1):17–26

    Article  MathSciNet  Google Scholar 

  12. Shayak B, Vyas P (2017) Krylov Bogoliubov type analysis of variants of the Mathieu equation. J Appl Nonlinear Dyn 6(1):57–77

    Article  MathSciNet  MATH  Google Scholar 

  13. Rajamani S, Rajasekar S (2017) Variation of response amplitude in parametrically driven single Duffing oscillator and unidirectionally coupled Duffing oscillators. J Appl Nonlinear Dyn 6(1):121–129

    Article  MathSciNet  Google Scholar 

  14. Luo ACJ (2012) Continuous dynamical systems. HEP/L&H Scientific, Beijing, Glen Carbon

    MATH  Google Scholar 

  15. Luo ACJ, Huang JZ (2012) Approximate solutions of periodic motions in nonlinear systems via a generalized harmonic balance. J Vib Control 18:1661–1871

    Article  MathSciNet  Google Scholar 

  16. Luo ACJ, Huang JZ (2012) Analytical dynamics of period-m flows and chaos in nonlinear systems. Int J Bifurc Chaos 22:1250093

    Article  MathSciNet  MATH  Google Scholar 

  17. Luo ACJ, Huang JZ (2012) Analytical routines of period-1 motions to chaos in a periodically forced Duffing oscillator with twin-well potential. J Appl Nonlinear Dyn 1:73–108

    Article  MATH  Google Scholar 

  18. Luo ACJ, Huang JZ (2012) Unstable and stable period-m motions in a twin-well potential Duffing oscillator. Discontinuity Nonlinearity Complex 1:113–145

    Article  MATH  Google Scholar 

  19. Wang YF, Liu ZW (2015) A matrix-based computational scheme of generalized harmonic balance method for periodic solutions of nonlinear vibratory systems. J Appl Nonlinear Dyn 4(4):379–389

    Article  Google Scholar 

  20. Luo ACJ (2013) Analytical solutions of periodic motions in dynamical systems with/without time-delay. Int J Dyn Control 1:330–359

    Article  Google Scholar 

  21. Luo ACJ, Jin HX (2014) Bifurcation trees of period-m motion to chaos in a time-delayed, quadratic nonlinear oscillator under a periodic excitation. Discontinuity Nonlinearity Complex 3:87–107

    Article  MATH  Google Scholar 

  22. Luo ACJ, Jin HX (2015) Complex period-1 motions of a periodically forced Duffing oscillator with a time-delay feedback. Int J Dyn Control 3:325–340

    Article  MathSciNet  Google Scholar 

  23. Luo ACJ, Jin HX (2014) Period-m motions to chaos in a periodically forced Duffing oscillator with a time-delay feedback. Int J Bifurc Chaos 24(10):1450126

    Article  MATH  Google Scholar 

  24. Luo ACJ (2015) Periodic flows in nonlinear dynamical systems based on discrete implicit maps. Int J Bifurc Chaos 25:1550044

    Article  MATH  Google Scholar 

  25. Luo ACJ, Guo Y (2015) A semi-analytical prediction of periodic motions in Duffing oscillator through mapping structures. Discontinuity Nonlinearity Complex 4(2):121–150

    Article  MathSciNet  MATH  Google Scholar 

  26. Guo Y, Luo ACJ (2017) Periodic motions in a double-well Duffing oscillator under periodic excitation through discrete mappings. Int J Dyn Control 5(2):223–238

    Article  MathSciNet  Google Scholar 

  27. Luo ACJ, Xing SY (2016) Symmetric and asymmetric period-1 motions in a periodically forced, time-delayed, hardening Duffing oscillator. Nonlinear Dyn 85(2):1141–1166

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical and Industrial Engineering, Southern Illinois University Edwardsville, Edwardsville, IL, 62026-1805, USA

    Siyuan Xing & Albert C. J. Luo

Authors
  1. Siyuan Xing
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Albert C. J. Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Albert C. J. Luo.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xing, S., Luo, A.C.J. Bifurcation trees of period-1 motions in a periodically excited, softening Duffing oscillator with time-delay. Int. J. Dynam. Control 7, 842–855 (2019). https://doi.org/10.1007/s40435-019-00520-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-019-00520-1

Keywords

Search

Navigation