INTRODUCTION

In recent years significant progress has been made in generating femtosecond and even attosecond extremely short light pulses [1–5]. The interest in their generation is mainly driven by the possibility of using such pulses to observe and control various ultrafast processes in matter, up to the dynamics of electrons in atoms and molecules [6–8]. Besides that, studying the nature and fundamental aspects of nonlinear optical phenomena on such timescales is of great interest as well [9–11]. The point is that, as numerous studies have shown, for such short light pulses the very nature of various processes of nonlinear light-matter interaction, such as the generation of optical harmonics [12, 13], the ionization of atoms [14, 15], coherent Rabi oscillations [16, 17] or the non-resonant excitation of quantum systems [18–20], undergoes fundamental changes.

One of the most important consequences of the unusual properties of the physics of subcycle pulses is the need to introduce a number of new physical quantities. These would have no significant practical relevance for long pulses containing many cycles of optical oscillations, but begin to play an important role in the case of subcycle pulses. One of these quantities is the electric pulse area defined by the expression

$${{\bar {S}}_{E}}(\bar {r}) = \int\limits_{ - \infty }^{ + \infty } \bar {E}(\bar {r},t{\kern 1pt} ')dt{\kern 1pt} '.$$
(1)

The electric pulse area (1) appears to be the most important quantity for describing the properties of unipolar half-cycle pulses, which represent the natural limit of pulse shortening when decreasing the number of optical cycles at a given central frequency. In particular, the value of the integral (1) determines the magnitude of the mechanical momentum transferred by a subcycle pulse when acting on a charged particle. It is also a key parameter that quantifies the effect of subcycle pulses on quantum systems in the case when the excitation pulse duration is shorter than the periods of resonant transitions in the system [18–21].

In addition, the electric pulse area (1) possesses the important property of being vortex-free in any non-magnetic medium:

$${\text{curl}}{\kern 1pt} {{\bar {S}}_{E}}(\bar {r}) = 0,$$
(2)

which follows directly from Maxwell’s equation [22–24]:

$${\text{curl}}{\kern 1pt} \bar {E}(\bar {r},t) = - \frac{1}{c}\frac{{\partial \bar {B}(\bar {r},t)}}{{\partial t}}.$$

In the simplest one-dimensional case, when linearly polarized light pulses with a plane wavefront propagate along the z-axis, Eq. (2) reduces to the simple form [22–24]

$$\frac{{d{{S}_{E}}}}{{dz}} = 0,\quad {\text{i}}{\text{.e}}.,\quad {{S}_{E}}(z) = {\text{const}}.$$
(3)

Thus, in the one-dimensional case, Eq. (3) represents the fundamental conservation rule of the electric area in space. The conservation rule (3) has been confirmed in many works on the subcycle pulse propagation in different media, including linear conducting media [25] and media with resonant [24, 26] or quadratic nonlinearity [27–31]. Due to its fundamental nature, the electric area conservation rule (3) can be applied to test the correctness of different approximations used to describe the propagation of subcycle pulses in different media.

In this paper, we will show what values the constant on the right-hand side of Eq. (3) can attain upon the propagation of subcycle pulses in non-magnetic media with both bound and free charges. Based on the obtained relations, we will analyze a number of approximate theoretical models, which are widely used to describe the interaction of subcycle pulses with different media, for their compatibility with the conservation rule of the electric area (3). It will be shown that for some approximations and some types of optical media violations of the conservation rule (3) are observed. These indicate the limited applicability of such approximate models and the possibility of obtaining unphysical results when using them uncritically.

GENERAL RELATIONS FOR THE VALUES OF THE ELECTRIC AREA

Consider the propagation of linearly polarized light pulses with a plane wavefront along the z-axis. The spatiotemporal dynamics of the electric field is then described using the one-dimensional wave equation:

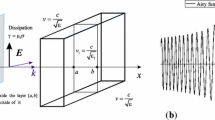
$$\frac{{{{\partial }^{2}}E}}{{\partial {{z}^{2}}}} - \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}E}}{{\partial {{t}^{2}}}} = \frac{{4\pi }}{{{{c}^{2}}}}\left( {\frac{{{{\partial }^{2}}P}}{{\partial {{t}^{2}}}} + \frac{{\partial j}}{{\partial t}}} \right),$$
(4)

where \(P(z,t)\) is the macroscopic polarization corresponding to bound charges in the medium, \(j(z,t)\) is the free-charge current density. In general, only at distances from the medium layer not exceeding the diffraction length such a one-dimensional consideration is valid. In addition, the one-dimensional model also describes the propagation of pulses in coaxial waveguides with no cut-off frequencies, so that the propagation of subcycle pulses, including unipolar pulses, turns out to be effectively one-dimensional [32].

The total field \(E(z,t)\) in the wave Eq. (4) is conveniently represented as the sum of the initial incident pulse and the medium emission. For the field emitted by a medium layer located in between the coordinates \({{z}_{1}}\) and \({{z}_{2}}\), the following general expression has been obtained in [33]:

$$\begin{gathered} {{E}_{{{\text{emit}}}}}(z,t) = - \frac{{2\pi }}{c}\int\limits_{{{z}_{1}}}^{{{z}_{2}}} \left[ {j\left( {z{\kern 1pt} ',t - \frac{{{\text{|}}z - z{\kern 1pt} '{\text{|}}}}{c}} \right)} \right. \\ \left. { + \;\frac{{\partial P}}{{\partial t}}\left( {z{\kern 1pt} ',t - \frac{{{\text{|}}z - z{\kern 1pt} '{\text{|}}}}{c}} \right)} \right]dz{\kern 1pt} '. \\ \end{gathered} $$
(5)

From Eq. (5) it is easy to obtain the expression for the electric area (1) emitted by the entire medium layer:

$$\begin{gathered} {{S}_{{{\text{emit}}}}}(z) = - \frac{{2\pi }}{c}\int\limits_{{{z}_{1}}}^{{{z}_{2}}} dz{\kern 1pt} '\int\limits_{ - \infty }^{ + \infty } j\left( {z{\kern 1pt} ',t - \frac{{{\text{|}}z - z{\kern 1pt} '{\text{|}}}}{c}} \right)dt \\ - \;\frac{{2\pi }}{c}\int\limits_{{{z}_{1}}}^{{{z}_{2}}} \left[ {P(z{\kern 1pt} ',t = + \infty ) - P(z{\kern 1pt} ',t = - \infty )} \right]dz{\kern 1pt} '. \\ \end{gathered} $$
(6)

In the case of a dielectric medium layer with no free charges in expressions (5) and (6) the first term disappears \(j(z,t) = 0\). In the case of a metal or plasma layer, where there are no bound charges, the macroscopic polarization is to be set zero instead \(P(z,t) = 0\).

A number of important conclusions can be directly drawn from the analysis of Eq. (6). Firstly, we note that Eq. (5) describes the emission of a medium layer both to the right and to the left. In this case, the radiation in both directions is identical only in the case of an infinitely thin medium layer. For a layer of finite thickness, due to the interference of radiation from different slices across the whole layer thickness the fields radiated by the layer to the right and to the left will be different. Nevertheless, their electric areas given by Eq. (6) will still be equal. This result is due to the infinite integration limits over time in Eq. (1), so that any time delays between the radiation from different parts of the medium do not play a role in the calculation of the electric area. Thus, Eq. (6) represents the electric area for both the radiation from a medium layer to the right and the radiation to the left.

Let us further assume that a subcycle pulse propagates in a dielectric medium without free charges, so that \(j(z,t) = 0\). We assume that the medium is in an equilibrium state with no induced macroscopic polarization before the pulse arrival and returns to this initial state after the pulse passage due to the inevitable presence of the relaxation of the macroscopic polarization. Then the integral in the second term on the right-hand side of (6) goes to zero:

$$\begin{gathered} {{S}_{{{\text{emit}}}}}(z) \\ = - \frac{{2\pi }}{c}\int\limits_{{{z}_{1}}}^{{{z}_{2}}} \left[ {P(z{\kern 1pt} ',t = + \infty ) - P(z{\kern 1pt} ',t = - \infty )} \right]dz{\kern 1pt} ' = 0. \\ \end{gathered} $$
(7)

The electric area radiated by the dielectric medium layer, or any part of it, is therefore zero. It should be noted that this conclusion is of a general type and is valid regardless of the specific characteristics of the incident pulse or the pulse sequence entering the medium and regardless of the parameters of the dielectric itself.

Let us now turn to the conservation rule of the electric area in the form (3). Assume the dielectric layer to have a finite thickness, the initial incident pulse with the electric area \({{S}_{{E,{\text{initial}}}}}\), the field radiated from the medium in the backward direction (i.e., reflected) having the electric area \({{S}_{{E,{\text{backward}}}}}\), and the field transmitted through the dielectric layer having the electric area \({{S}_{{E,{\text{forward}}}}}\). Since from that side of the layer the initial pulse comes from there is first the initial pulse passes through each spatial point and afterwards with some delay the reflected field does, the conservation rule of the electric area (3) takes the form

$${{S}_{{E,{\text{initial}}}}} + {{S}_{{E,{\text{backward}}}}} = {{S}_{{E,{\text{forward}}}}}.$$
(8)

The obtained relation (8) is also valid at any point inside the dielectric layer with the corresponding change of notation for the terms, if we rewrite it in the form:

$$\begin{gathered} {{S}_{{E,{\text{initial}}}}} + {{S}_{{E,{\text{backward}}}}}(z) + {{S}_{{E,{\text{forward}}}}}(z) \\ = {{S}_{E}}(z) = {\text{const}}. \\ \end{gathered} $$
(9)

The second term on the left-hand side of (9) is now the electric area of the backward radiation from that part of the layer which is located further along the propagation direction of the initial pulse relative to the given point in space. At the same time, the third term on the left-hand side of (9) is now the electric area of the forward radiation from the part of the layer that is located earlier in the propagation direction of the initial pulse relative to this point in space. Note that the first term on the left-hand side of (9), i.e., the electric area of the initial pulse, is by definition constant and does not depend on the z coordinate, unlike the other two terms.

The field radiated from a dielectric layer or any part of it, both forwards and backwards, always has zero electric area according to Eq. (7). Hence, for any dielectric medium in Eq. (9) we obtain:

$${{S}_{{E,{\text{backward}}}}}(z) = {{S}_{{E,{\text{forward}}}}}(z) \equiv 0.$$
(10)

Accordingly, Eq. (9), which expresses the electric area conservation rule, takes the form:

$${{S}_{E}}(z) = {\text{const}} = {{S}_{{E,{\text{initial}}}}}.$$
(11)

Thus, the electric area as a function of the coordinate in space can take as its constant value any one equal to the electric area of the initial pulse incident on a dielectric medium. Note that the obtained expressions (7), (10), (11) are valid only for a dielectric medium in which there are only bound charges, but are not obeyed in the presence of free charges in the medium, i.e., if \(j(z,t) \ne 0\) on the right-hand side in Eqs. (5) and (6). In the following chapters, the obtained relations (6)–(11) will be applied to analyze the correctness of several approximate approaches for the theoretical description of the propagation of subcycle pulses in various linear and nonlinear media.

To illustrate the obtained relation (11), let us consider the propagation of a unipolar half-cycle pulse through a layer of a two-level medium. The response of a two-level medium is described by the standard equations for the dynamics of the medium density matrix [34]:

$$\frac{{\partial {{\rho }_{{12}}}(z,t)}}{{\partial t}} = - \frac{{{{\rho }_{{12}}}(z,t)}}{{{{T}_{2}}}}$$
$$ + \,i{{\omega }_{{12}}}{{\rho }_{{12}}}(z,t) - \frac{i}{\hbar }{{d}_{{12}}}E(z,t)n(z,t),$$
$$\frac{{\partial n(z,t)}}{{\partial t}} = - \frac{{n(z,t) - {{n}_{0}}(z)}}{{{{T}_{1}}}} + \frac{4}{\hbar }{{d}_{{12}}}E(z,t){\text{Im}}{\kern 1pt} {{\rho }_{{12}}}(z,t),$$
$$P(z,t) = 2{{N}_{0}}{{d}_{{12}}}{\text{Re}}{\kern 1pt} {{\rho }_{{12}}},$$
(12)

where \(E\) is the electric field strength, \(P\) is the induced macroscopic polarization of the medium, \({{\rho }_{{12}}}\) is the off-diagonal element of the density matrix of the two-level medium, \(n = {{\rho }_{{11}}} - {{\rho }_{{12}}}\) is the population difference in the two-level medium, \({{d}_{{12}}}\) is the dipole moment of the resonant transition, \({{\omega }_{{12}}}\) is the transition frequency, \({{N}_{0}}\) is the particle density, \({{n}_{0}}\) is the equilibrium population difference in the absence of the electric field (\({{n}_{0}} = 1\) for an absorbing medium), \({{T}_{1}}\) is the lifetime of the upper level, \({{T}_{2}}\) is the phase relaxation time in the medium, c is the speed of light in vacuum, \(\hbar \) is the reduced Planck’s constant.

The system of Eqs. (12) was solved numerically together with the wave Eq. (4) in the absence of any currents \(j(z,t) = 0\). In the calculations we considered the layout, when a unipolar half-cycle pulse of a non-zero electric area (1), i.e., a pulse of Gaussian shape, hits normally an optically thick layer of a two-level medium:

$$E(z = 0,t) = {{E}_{0}}{{e}^{{ - {{t}^{2}}/{{\tau }^{2}}}}},$$
(13)

with the pulse amplitude \({{E}_{0}}\) and the duration \(\tau \). The results of the numerical simulations are shown in Fig. 1. The amplitude of the initial pulse \({{E}_{0}}\) and the spatial density of particles \({{N}_{0}}\) were chosen as variable parameters. The thickness of the medium layer was chosen to be one order of magnitude larger than the wavelength of the resonant transition. As can be seen from Fig. 1, the conservation rule of the electric area in space (3) is satisfied for all parameter values considered. Moreover, the obtained constant values of the electric area are in all cases exactly equal to the electric area of the initial incident pulse (13) (the corresponding values are represented by crosses on the vertical axis in Fig. 1). Thus, the results of the numerical simulations are in exact agreement with the general analytical results obtained above and given by Eqs. (10) and (11).

Fig. 1.
figure 1

(Color online) Spatial dependence of the electric area (1) when a unipolar half-cycle pulse of Gaussian shape (13) passes through a layer of a two-level medium. The thickness of the medium layer \(L = 20\) μm, the medium parameters \({{d}_{{12}}} = 10{\kern 1pt} \) D, \({{\omega }_{{12}}}{{ = 10}^{{15}}}{\kern 1pt} \) s–1, \({{n}_{0}} = 1\), \({{T}_{1}} = 100{\kern 1pt} \) fs, \({{T}_{2}} = 20{\kern 1pt} \) fs, the duration of the incident pulse \(\tau = 1{\kern 1pt} \) fs. The incident pulse amplitude \({{E}_{0}}\) and the spatial density of resonant centers \({{N}_{0}}\) were varied. Crosses of the respective colors on the vertical axis mark the values of the electric area of the initial incident pulses (13) for all considered parameter sets. The black dashed vertical lines indicate the boundaries of the medium layer.

Full size image

PROPAGATION OF SUBCYCLE PULSES IN A TWO-LEVEL MEDIUM

We start our consideration with approximate models of the coherent propagation of subcycle pulses in a resonant optical medium. The simplest approach, but also the most important from a methodological viewpoint, is to describe the medium in terms of a two-level model. This situation was first studied in detail in the works of E.M. Belenov and A.V. Nazarkin [35–37], where the propagation of subcycle pulses in an amplifying or absorbing two-level resonant medium was studied in the limit of pulse durations \(\tau \) much shorter than the period of the resonant transition of the medium, i.e.,

$${{\omega }_{{12}}}\tau \ll 1.$$

In this limiting case, a sine-Gordon equation of the following form was obtained for the spatiotemporal dynamics of the electric field in the medium:

$$\frac{{{{\partial }^{2}}\Psi }}{{\partial {{z}^{2}}}} - \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}\Psi }}{{\partial {{t}^{2}}}} = \alpha \sin \Psi ,$$
(14)

where the following quantity is used:

$$\Psi (z,t) = \frac{{2{{d}_{{12}}}}}{\hbar }\int\limits_{ - \infty }^t E(z,t{\kern 1pt} ')dt{\kern 1pt} ',$$

i.e., the time integral of the electric field with a finite upper limit. Here d12 is the dipole moment of the resonant transition in a two-level medium, α is the coupling factor:

$$\alpha = \frac{{8\pi {{\omega }_{{12}}}{{N}_{0}}d_{{12}}^{2}{{n}_{0}}}}{{\hbar {{c}^{2}}}},$$

the sign of which depends on whether the medium is amplifying or absorbing.

Let we now consider the limit \(t \to + \infty \) in the sine-Gordon equation (14). Assume that we are dealing with limited in time electromagnetic pulses, so that the electric field everywhere goes to zero at \(t \to + \infty \). Such a complete damping of the field in any real medium is provided by the dissipation mechanisms inevitably present in it, leading to a gradual decay of the field in the course of time. As the electric field goes to zero at \(t \to + \infty \), the time-domain derivative of \(\Psi (z,t)\) and hence the second term on the left-hand side of Eq. (14) also goes to zero. The value \(\Psi (z,t)\) in such a limit turns into the electric area (up to a constant factor), and Eq. (14) takes the form:

$$\frac{{{{d}^{2}}{{S}_{E}}}}{{d{{z}^{2}}}} = \frac{{\hbar \alpha }}{{2{{d}_{{12}}}}}\sin \frac{{2{{d}_{{12}}}{{S}_{E}}}}{\hbar }.$$
(15)

The comparison of the conservation rule for the electric area (3) and the sine-Gordon equation for the electric area (15) shows that these equations are compatible only if the right-hand side of Eq. (15) equals zero:

$$\frac{{2{{d}_{{12}}}}}{\hbar }{{S}_{E}}(z) = {\text{const}} = 0, \pm \pi , \pm 2\pi , \pm 3\pi , \ldots ,$$
(16)

i.e., only if the electric area is constant in space and is a multiple of \(\pi \) (in the units \(\hbar {\text{/}}2{{d}_{{12}}}\)). However, according to the obtained expression (11), the value of the constant in Eq. (3) can take any value in a dielectric medium. In fact, Maxwell’s equations in their general form do not impose any restrictions on the possible values of the electric pulse area and, in particular, do not imply any quantization of this quantity. On the contrary, Maxwell’s equations allow the existence and stable propagation of any unipolar pulses in space at the speed of light, regardless of the value of their electric area [38–40].

The reason for this contradiction in this case is the elimination of all relaxation terms in the equations for the response of a two-level resonant medium upon the derivation of Eq. (14). As a result, under such conditions only those pulses can stably propagate in the two-level medium, at the trailing edge of which the induced medium polarization returns exactly to its initial zero value, i.e., when the right-hand side of (15) vanishes. At the same time, keeping all relaxation terms in the equations for the medium response would avoid the appearance of any artificial quantization of the electric area according to Eq. (16). Note also that if the relaxation processes in the medium are neglected, the medium oscillators, excited even by a very short pulse, can oscillate infinitely long, while continuously emitting electromagnetic waves, which would also violate the energy conservation law.

It is worth noting that, although Eq. (15) is simpler than the sine-Gordon equation (14) and allows us to easily find spatially uniform solutions for the electric area (16), it is not suitable for the numerical simulations. Indeed, in order to find a particular solution of Eq. (15) it is necessary to set the initial conditions at some point in space. For this purpose, it is not sufficient to know only the electric area of the initial pulse incident on the medium. In fact, on the side of the medium from which the initial pulse is incident, the incident pulse first passes through each point and then with some delay the reflected field passes. Therefore, in order to set the initial conditions for the electric area at any point in Eq. (15), we need to know in advance the value of the electric area of the reflected (or transmitted) field. However, these values can only be obtained by numerically solving the sine-Gordon equation (14) for the electric field strength. Hence, the general sine-Gordon equation (14) must be solved in order to find out the electric area \({{S}_{E}}(z)\).

Figure 2 shows the results of the numerical modeling of a unipolar half-cycle pulse (13) passing through a layer of a two-level medium by means of the sine-Gordon equation (14). As can be seen from Fig. 2, although the electric area appears to be constant in space, it only takes discrete values according to Eq. (16). In this case, the specific value of the electric area is determined by the value of the electric area of the initial incident half-cycle pulse (13). More precisely, for each of the solutions (16) there is an interval of values of the electric area of the initial pulse (13), within which the electric area \({{S}_{E}}(z)\) converges exactly to this solution out of the discrete set (16). It is important to emphasize that, as shown in Fig. 2, the resulting value of the electric area in space is in general significantly different from the electric area of the initial incident pulse, which contradicts the exact analytical solution (11).

Fig. 2.
figure 2

(Color online) Spatial dependence of the electric area (1), when a unipolar half-cycle pulse of Gaussian shape (13) passes through a layer of a two-level medium described by the sine-Gordon equation (14). The thickness of the medium layer is \(L = 20\) μm, the medium parameters are \({{d}_{{12}}} = 10\) D, \({{\omega }_{{12}}}{{ = 10}^{{15}}}\) s–1, \({{N}_{0}} = \) 1019 cm–3, \({{n}_{0}} = 1\), and the duration of the incident pulse is \(\tau = 1{\kern 1pt} \) fs. The amplitude of the incident pulse \({{E}_{0}}\) was varied. Crosses on the vertical axis indicate the values of the electric area of the initial incident pulses (13) for the corresponding values of their amplitude \({{E}_{0}}\). The black vertical lines indicate the boundaries of the medium layer.

Full size image

Our conclusion is therefore that the sine-Gordon equation (14) is not in accordance with the fundamental conservation rule of the electric area (3). This means that the sine-Gordon equation (14) can only have a limited applicability range and all its solutions must be modified to ensure that the fundamental conservation rule of the electric area is fulfilled.

UNIDIRECTIONAL APPROXIMATION FOR SUBCYCLE PULSES

The most commonly used approximation to describe the propagation of ultra-short pulses is the slowly varying envelope approximation (SVEA). However, for subcycle pulses this approximation becomes obviously incorrect already for pulses with just a few cycles, and even more so for subcycle pulses.

The unidirectional approximation [41, 42] is often used as a possible alternative that allows simplification of the corresponding theoretical models for subcycle pulses. This approximation is based on the neglecting of the backward propagating wave and implies that the field in the medium moves only in the direction of the incident pulse with a velocity equal to or close to the respective linear velocity.

As shown by the authors in [43], for the propagation of a half-cycle unipolar pulse in the framework of the unidirectional approximation in plasma the electric area is not conserved. Instead, it decreases exponentially as the pulse moves deeper into the plasma. At the same time, even in the unidirectional approximation, the fundamental conservation rule (3) remains valid for the propagation of a half-cycle unipolar pulse in a dielectric medium [44].

To clarify the origin of the resulting deviations from the conservation rule (3), we first recall the results obtained earlier in this paper for dielectric media. Namely, as mentioned above, radiation from a dielectric layer, or any part of it, both forward and backward always has zero electric area according to Eq. (7). In particular, this means that the electric area of that part of the field going in the backward direction is zero, see Eq. (10). Thus, neglecting the presence of the reflected wave does not lead to a violation of the conservation rule of the electric area (3). Thus, in the case of subcycle pulse propagation in a dielectric medium, applying the unidirectional approximation does not lead to any deviations from the exact conservation rule (3).

Let us now consider the opposite situation, when a subcycle pulse propagates in a plasma or metal with no bound charges, i.e., \(P(z,t) = 0\), so that there are only free charges. In such a case, only the first term in Eq. (6) remains, which contains the current density of free charges \(j(z,t)\) under the integral sign, and this integral in Eq. (6) in general does not equal zero. Thus, the electric area of the plasma layer emission is different from zero. The reason for this peculiarity can be understood directly from Eq. (6). In fact, the first term in (6) represents the total charge passing through the cross section of the plasma layer perpendicular to the polarization direction of the incident field. Due to the one-dimensional problem setup, which implies infinitely large sizes of the medium layer in transverse dimensions, and due to the presence of free charges in the medium, such a total charge will generally be non-zero. This means that there is a parallel charge transfer in the transverse plane, which in the one-dimensional problem does not lead to the formation of uncompensated charges anywhere. Instead, it determines a non-zero value of the electric area of the emitted field from a metal or plasma layer. It should be noted that this result is valid not only for a medium in which free charges were initially present, but also for a dielectric medium in which the ionization and formation of free charges occur under the action of the incident subcycle pulse itself.

In this case, the conservation rule in the form (8) or (9) is still valid in the sense discussed above for the case of a dielectric medium. However, in the case of a plasma medium, the electric area of the reflected field \({{S}_{{E,{\text{backward}}}}}\), i.e., the field radiated in the backward direction by a medium layer or any part of this layer, is different from zero. Hence, according to (8) and (9) the electric area of the field that has passed through the plasma layer or any part of this layer is different from the electric area of the initial pulse \({{S}_{{E,{\text{initial}}}}}\) (or series of pulses) incident on the medium.

This result means that neglecting the presence of the reflected field upon the propagation of subcycle pulses in a plasma or metal inevitably leads to a deviation from the exact conservation rule of the electric area (3). Since the unidirectional approximation implies that the reflected (backward) wave is not taken into account, we conclude that the electric area conservation rule (3) will always be violated when describing the one-dimensional propagation of subcycle pulses in a plasma or metal within the framework of the unidirectional approximation. This conclusion is in agreement with the results of [43] and the subsequent comment [45]. At the same time, it explains the reason for the alleged violation of the conservation rule (3) obtained by the authors in [43].

PROPAGATION OF SUBCYCLE PULSES IN A LINEAR DISPERSIVE MEDIUM (PLASMA)

Let us further consider the propagation of subcycle pulses in a linear medium with strong dispersion. We start from the results of [46], where some exactly solvable models of the interaction of ultra-short pulses containing one or more field oscillations with some classes of dielectrics and conductors were investigated. The one-dimensional Klein–Fock–Gordon equation for the propagation of a plane linearly-polarized wave in a cold, collisionless, homogeneous and fully ionized gas plasma is used there as the basic universal model for describing unsteady wave processes in media with dispersion. The induced current density \(j(z,t)\) in such a plasma is given by the following eq-uation:

$$\frac{{\partial j}}{{\partial t}} = \frac{{{{\Omega }^{2}}}}{{4\pi }}E,$$
(17)

where \(\Omega \) is the plasma frequency. Substituting this expression into the right-hand side of the wave Eq. (4), we obtain:

$$\frac{{{{\partial }^{2}}E}}{{\partial {{z}^{2}}}} - \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}E}}{{\partial {{t}^{2}}}} = \frac{{{{\Omega }^{2}}}}{{{{c}^{2}}}}E.$$
(18)

Let us now integrate the obtained Eq. (18) over time in infinite limits, taking into account that all processes of pulses interaction with the medium are limited in time. Then the electric field and its time-domain derivative become zero everywhere at \(t \to \pm \infty \) so that the following equation for the spatial distribution of the electric area \({{S}_{E}}(z)\) is obtained from Eq. (18):

$$\frac{{{{d}^{2}}{{S}_{E}}}}{{d{{z}^{2}}}} = \frac{{{{\Omega }^{2}}}}{{{{c}^{2}}}}{{S}_{E}}.$$
(19)

The general solution of Eq. (19) has the form:

$${{S}_{E}}(z) = {{C}_{1}}{{e}^{{\Omega z/c}}} + {{C}_{2}}{{e}^{{ - \Omega z/c}}}.$$
(20)

Except for the trivial special case \({{C}_{1}} = {{C}_{2}} = 0\), Eq. (20) obviously contradicts the conservation rule of the electric area (3).

The above consideration once again demonstrates the importance and usefulness of the conservation rule of the electric area (3). In this case, the discrepancy is due to the neglecting the current damping in a dispersive medium. Indeed, we can take into account the collisions in the plasma by adding a relaxation term to the right-hand side of the dynamical Eq. (17) with the effective relaxation coefficient \(\gamma \):

$$\frac{{\partial j}}{{\partial t}} = - \gamma j + \frac{{{{\Omega }^{2}}}}{{4\pi }}E,$$
(21)

so that instead of Eq. (19) we obtain:

$$\frac{{{{d}^{2}}{{S}_{E}}}}{{d{{z}^{2}}}} = \frac{{{{\Omega }^{2}}}}{{{{c}^{2}}}}{{e}^{{ - \gamma t}}}\int\limits_{ - \infty }^t {{e}^{{\gamma t{\kern 1pt} '}}}E(t{\kern 1pt} ')dt{\kern 1pt} '{{{\text{|}}}_{{t \to + \infty }}} = 0.$$
(22)

Here, the expression on the right-hand side tends to zero at \(t \to + \infty \) since the integral over time in the last factor tends to a finite constant value due to the assumed limited pulse duration in time. The general solution of Eq. (22) is then written in the following simple form:

$${{S}_{E}}(z) = {{C}_{1}} + {{C}_{2}}z,$$
(23)

where it is necessary to set \({{C}_{2}} = 0\) in order to avoid the infinite increase or decrease in the electric area in space, which has no physical meaning. This is now exactly the conservation rule of the electric area (3), which confirms the fundamental importance of taking into account the relaxation processes in a dispersive medium to obtain a correct description of subcycle pulse propagation in it.

In order to verify the obtained relations (22) and (23), a joint numerical solution of Eqs. (4) and (21) was performed. The unipolar half-cycle pulse (13) was again used as the initial incident pulse. The results of the numerical simulations for different values of the relaxation coefficient \(\gamma \) are shown in Fig. 3. It can be seen that the electric area conservation rule (3) is exactly fulfilled according to Eq. (23). At the same time, the specific value of the constant on the right-hand side of Eq. (3) depends strongly on the value of the relaxation coefficient \(\gamma \), and the value of the electric area decreases rapidly as the relaxation in the plasma decreases.

Fig. 3.
figure 3

(Color online) Spatial dependence of the electric area (1) when a unipolar half-cycle pulse of Gaussian shape (13) passes through a layer of the dispersive plasma at different values of the relaxation coefficient \(\gamma \). The thickness of the medium layer \(L = 20\) μm, the plasma frequency of the medium \(\Omega = 3 \times {{10}^{{14}}}\) s–1, the incident pulse has the duration \(\tau = 1{\kern 1pt} \) fs and the amplitude \({{E}_{0}}{{ = 10}^{5}}\) ESU.

Full size image

At the same time, the numerical solution of Eq. (18) for a collisionless plasma (i.e., at zero relaxation coefficient \(\gamma \)) shows that for any values of the parameters of the plasma layer and the incident pulse, the electric area goes everywhere to zero, i.e., this solution corresponds to the general solution (20) in the special case when \({{C}_{1}} = {{C}_{2}} = 0\). The reason for this behavior of the electric area can be understood from the following general considerations. According to the general solution of the wave Eq. (5), the plasma layer keeps radiating until the density of the free-charge currents becomes zero everywhere, i.e., it must be \(j(z,t) \to 0\) at \(t \to + \infty \). However, by direct integration of Eq. (17) it is easy to obtain that:

$$j(z,t) = \frac{{{{\Omega }^{2}}}}{{4\pi }}\int\limits_{ - \infty }^t E(z,t{\kern 1pt} ')dt{\kern 1pt} ',$$
(24)

so that at \(t \to + \infty \) the current density is directly proportional to the value of the electric area at this point. Then it follows directly from Eq. (24) that the zero value of the current density entails the zero value of the electric area in the whole space. Thus, although the general solution (20) means in general spatially-inhomogeneous solutions for a plasma layer without losses, only solutions with zero electric area are physically possible in such a medium.

It is also of interest to consider how the value of the electric area (constant in space) shown in Fig. 3 depends on the thickness of the plasma layer. The corresponding numerical simulation results are shown in Fig. 4 (in logarithmic scale) at a fixed value of the relaxation coefficient \(\gamma \) (red circles). Note that the values of the electric area shown in Fig. 3 are equal, in particular, to the electric area of the pulse transmitted through the plasma layer. Indeed, from the side of the plasma layer opposite to that from which the initial pulse (13) arrives, only the field that has passed through the entire plasma layer passes through each point. Hence, the graph in Fig. 4 shows, among others, the dependence of the electric area of the pulse transmitted through the plasma layer on the thickness of this layer.

Fig. 4.
figure 4

(Color online) Dependence of the constant value of the electric area on the right-hand side of Eq. (3) on the thickness of the plasma layer when a unipolar half-cycle pulse of Gaussian shape (13) passes through it: the results of numerical simulations (red circles) and the exact analytical solution (27) (blue solid line). The green dashed line shows the approximate analytical solution (28) obtained in [43] under the unidirectional approximation. The plasma frequency of the medium is \(\Omega = 3 \times {{10}^{{14}}}\) s–1, the relaxation coefficient is \(\gamma {{ = 10}^{{14}}}\) s–1, the incident pulse has the duration \(\tau = 1{\kern 1pt} \) fs and the amplitude \({{E}_{0}}{{ = 10}^{5}}\) ESU. The cross on the vertical axis indicates the value of the electric area of the initial incident pulse (13).

Full size image

The dependence of the electric area of the transmitted pulse on the thickness of the plasma layer, shown in Fig. 4, can be described analytically. To do this, consider the standard problem of the normal incidence of a plane wave of the frequency \(\omega \) on a plane-parallel plate of the thickness \(L\) made of a material with the refractive index \(n(\omega )\). If the amplitude of the incident plane wave is equal to \({{A}_{{{\text{inc}}}}}\), the amplitude of the transmitted wave \({{A}_{{{\text{tr}}}}}\) is determined by the expression [47]

$${{A}_{{{\text{tr}}}}} = \frac{{4n(\omega )}}{{{{{(n(\omega ) + 1)}}^{2}} - {{{(n(\omega ) - 1)}}^{2}}{{e}^{{2i\omega Ln(\omega )/c}}}}}{{A}_{{{\text{inc}}}}}.$$
(25)

The refractive index for a plasma or metal within the Drude–Lorentz model has the form:

$$n(\omega ) = \sqrt {1 - \frac{{{{\Omega }^{2}}}}{{\omega (\omega + i\gamma )}}} ,$$
(26)

which follows directly from Eq. (21).

Let us now go in Eq. (25) and (26) to the limit \(\omega \to 0\). As can be seen from Eq. (1), the electric area is actually the Fourier spectral component of the field at the zero frequency. Thus, in this limit, the spectral components \({{A}_{{{\text{inc}}}}}\) and \({{A}_{{{\text{tr}}}}}\) turn into the electric areas of the incident pulse \({{S}_{{{\text{inc}}}}}\) and the field \({{S}_{{{\text{tr}}}}}\) that has passed through the layer, respectively. Let us now consider what happens to the right-hand side of Eq. (25) in this limiting case \(\omega \to 0\). By combining (25) and (26) and omitting the terms with powers of \(\omega \) higher than one, we can easily obtain the limiting expression:

$${{S}_{{{\text{tr}}}}} \to \frac{1}{{1 + \frac{{{{\Omega }^{2}}L}}{{2\gamma c}}}}{{S}_{{{\text{inc}}}}}.$$
(27)

Expression (27) thus represents the value of the constant on the right-hand side of the conservation rule (3) in the case of subcycle pulse propagation through a plasma or metal layer described by the Drude–Lorentz model (21), (26).

The analytically calculated dependence (27) is shown in Fig. 4 by a solid blue line. It is easy to see that the numerical results are in perfect agreement with the theoretical curve (27). Note that in the limit \(\gamma \to 0\) (ideal collisionless plasma) the expression on the right-hand side of (27) goes to zero, which is also in full agreement with the numerical simulation results described above.

The obtained dependence can be confronted with the results of [43], where an analytical solution for the electric area of a pulse propagating in a plasma was obtained in the unidirectional approximation. In particular, in the notation of the model used (21), the dependence of the electric area of the propagating pulse on the propagation length obtained in [43] can be written in the form

$${{S}_{E}}(z) = {{S}_{E}}(0)\exp \left( { - \frac{{{{\Omega }^{2}}}}{{2\gamma c}}z} \right),$$
(28)

i.e., the electric area decreases exponentially as the pulse propagates in the layer. The dependence (28) is also shown in Fig. 4 (green dashed line) for clarity. As can be clearly seen from the comparison of two curves in Fig. 4, the unidirectional approximation describes very poorly the real behavior of the electric area vs the thickness of the plasma layer. Upon the exact solution of the full (bidirectional) wave Eq. (4) the electric area of the transmitted pulse decreases when increasing the layer thickness much slower than the exponential law (28) according to the dependence, which turns out to be quite close to the power-law one \( \sim {\kern 1pt} {{L}^{{ - 1}}}\). The main reason for such a significant discrepancy, as already noted in the previous section, is the complete neglecting the backward wave within the unidirectional approximation. In fact, the unidirectional approximation is based on the assumption that the macroscopic polarization induced in the medium provides only a small perturbation of the incident pulse. In the case of a plasma layer with the parameters shown in Figs. 3 and 4, the significant reflection occurs at a layer thickness of just about one micron. Thus, the assumption of a small perturbation of the incident pulse by the medium layer is obviously violated.

Finally, it is also worth noting that in the limit \(\omega \to 0\) the following asymptotic expression is valid for the wavenumber of a monochromatic wave in a plasma or metal with the dispersion relation (26):

$$k(\omega ) = \frac{\omega }{c}n(\omega ) \sim \sqrt \omega \to 0,$$

i.e., the wavenumber vanishes in this limit. This result means that, when solving the problem of a monochromatic plane wave propagation through a medium layer (26), the amplitudes of both the forward and backward waves inside the layer, which are proportional to \({{e}^{{ \pm ik(\omega )z}}}\) in the limit \(\omega \to 0\) do not depend on the coordinate z, i.e., they are constant in space (inside the medium layer). This conclusion also contradicts the approximate solution (28), according to which the electric area of the forward wave within the medium layer (26) should decay exponentially.

CONCLUSIONS

In conclusion, this paper has theoretically addressed the correctness issues of approximate theoretical models used to describe the propagation of extremely short pulses in various media. The fundamental conservation rule of the electric area, derived directly from Maxwell’s equations in the one-dimensional setup, has been used as the main criterion of correctness.

The analysis performed has shown that some commonly used approximations lead to the violation of the electric area conservation rule. In particular, this applies to the sine-Gordon equation for coherent propagation of subcycle pulses in a two-level resonant medium and the unidirectional approximation for the propagation of subcycle pulses in metals or plasma. The main reasons for the violation of this conservation rule are either the neglect of dissipation processes in the medium or the neglect of the backward wave. In these cases, it is necessary to correct all the solutions obtained within the framework of these approximate models by adding some extra correction terms that guarantee the conservation of the electric area.

It is important to note that the proposed approach can be used directly to determine the applicability limits of any other approximation for the propagation of subcycle pulses in arbitrary linear and nonlinear media. Such an analysis can also be based on the use of other conservation laws, in particular the energy conservation law. However, in the case of subcycle pulses it is the electric area (1) which turns out to be the most convenient quantity for checking the accuracy of theoretical models due to its linear dependence on the electric field and its crucial role in the pulse interaction with quantum systems.