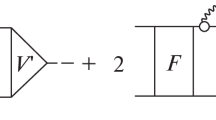Spreading Widths of Giant Monopole Resonance in the Lead Region: Random Matrix Approach

The microscopic calculation of the decay width of giant monopole resonance (GMR) anticipates the mixing of one-phonon states with configurations of increasing complexity. To this aim we develop the effective approach for description of monopole excited states that are obtained in the quasiparticle random phase approximation (QRPA), with regard of the coupling between one- and two-phonon states. Based on the QRPA one-phonon states, we generate the coupling and two-phonon states by means of the Gaussian orthogonal ensemble (GOE) distribution. Within our approach the spreading width of the GMRs in ^204,206,208Pb are described by means of a random matrix approach on two energy scales. It is demonstrated that the main contribution into the decay of the GMR is determined by a small number of two-phonon states strongly coupled to low-energy surface vibrations. While a vast majority of the coupling matrix elements (that are small in value and following the GOE distribution) are responsible for the fine structure of the GMR spreading width. A remarkable agreement between the results of the full microscopic calculations (based on QRPA phonons coupled by means of the microscopic coupling matrix elements with calculated two-phonon states) with those of the developed approach confirms the vitality of the proposed ideas.

INTRODUCTION

Response of a finite quantum system to external excitations is one of the oldest but still among most important subjects in quantum many-body theory. Evidently, the increase of the excitation energy results in rise of level density of the excited states of such a system. Consequently, decay properties of the single-particle states and collective excitations of a system under consideration may be described statistically above the particle emission threshold, with a high degree of disorder (see in context of nuclear physics, e.g., [1, 2]).

Among various phenomena, related to this concept, the decay of giant nuclear resonances (GRs) remains to be a topical subject in nuclear structure theory during a few decades [3–7]. Giant resonance states can be excited, for instance, by the nucleon-nucleus scattering, by stripping of a nucleon from the projectile in the collision of two nuclei, or by electromagnetic radiation. Contrary to the above statistical concept, GRs involve many nucleons in a coherent motion and are characterized by definite quantum numbers (spin, parity, isospin), rather than a chaotic dynamics of uncorrelated particles.

Yet the analysis of nuclear collective properties of GRs requires as well the consideration of their coupling with a stochastic background of compound states (see, e.g., [8–11] and references therein). According to a general wisdom, the wave function of a particular GR is rather spread over the eigenstates of the nuclear Hamiltonian, carrying the same quantum numbers. In other words, in microscopic approaches, for a particular reaction GR serves as a doorway state that is coupled to a set of background states via real coupling matrix elements (see, e.g., [12, 13]).¹ As a result, such a state manifests itself as a broad maximum in the strength function $S(E) = \sum\nolimits_k {\text{|}}\langle k{\text{|}}F{\text{|}}0\rangle {{{\text{|}}}^{2}}\delta (E - {{E}_{k}})$. Here the matrix element $\langle k{\text{|}}F{\text{|}}0\rangle$ of the operator F, acting on the initial state ${\text{|}}0\rangle$, creates the eigenstates of the nuclear Hamiltonian. It is generally accepted that the decay evolution of the doorway states over the hierarchy of more complex configurations to compound states determines the spreading width ${{\Gamma }^{ \downarrow }}$. Together, with the Landau damping $({{\Gamma }_{L}})$ and the escape width $({{\Gamma }^{ \uparrow }})$, the spreading width forms the decay width Γ = ${{\Gamma }_{L}} + {{\Gamma }^{ \downarrow }} + {{\Gamma }^{ \uparrow }}$ of a GR. We recall that the Landau damping describes the fragmentation of one-particle–one-hole $(1p{-} 1h)$ excitations, while the escape width corresponds to direct particle emission into the continuum.

With recent development of semiconductor detectors and computer facilities there is a desire to understand, at least, the basic principles of decay mechanisms of various GRs, their common and distinctive properties. The general idea on GR decay properties as a consequence of the coupling of high-lying modes with the lowest collective vibrational modes [3] requires further development in light of discussion on the role of order and disorder in nuclei [14, 15]. We recall, however, that the analysis of spreading widths, associated with the cascade of couplings and their fragmentations due to these couplings (cf. [16–19]), is a real challenge for nuclear structure theory. In fact, even modern computer facilities are unable to trace the decay of the doorway state over the hierarchy due to the tremendous numerical obstacles. Nowadays, most successful attempts in this direction are restricted by the consideration of the microscopic coupling between one-phonon and two-particle-two-hole $(2p{-} 2h)$ or two-phonon configurations (see, e.g., discussion in [4, 6, 20–24]).

In this paper we suggest the alternative approach, based on ideas of the Random Matrix Theory (RMT) [1, 25], which enables us to count effectively the problem of the hierarchy at the description of spreading widths. To provide a detailed overview of our approach we consider only spherical or near-spherical nuclei around ²⁰⁸Pb, and focus our attention on the decay width $\Gamma \approx {{\Gamma }_{L}} + {{\Gamma }^{ \downarrow }}$ of the GMRs. The escape width $({{\Gamma }^{ \uparrow }}$) is neglected in our approach, since its contribution is negligible for heavy nuclei. It is noteworthy that a wide interest to the decay properties of GMRs stems from the intention to extrapolate from these properties the incompressibility of uniform nuclear matter (see for a review [26–28]). More importantly for our discussion, that in the description of GMRs there is a need for inevitable accounting of the microscopic coupling between one-phonon and $2p{-} 2h$ configurations for correct interpretation of experimental data (see details for a chain of nuclei in [29]). Furthermore, it was stated that more complex configurations may further improve the agreement with the experimental data. We shall demonstrate that GMR spreading widths can be successfully simulated by means of the RMT approach, based on the microscopic QRPA calculations.

THEORETICAL FRAMEWORK

It appears that the main mechanism responsible for spreading widths differs for different GRs. In particular, it was shown in [21] that the coupling with the low-lying surface vibrations provides quite satisfactory description of the width of the isoscalar quadrupole GR (ISQGR). It seems that the Landau damping yields the major contribution to the gross structure of the isovector dipole GR (IVDGR) [30–32]. However, the incorporation of ideas, borrowed from the RMT, providing the effective counting of the two-phonon configurations, contributed additionally to redistribution of the isovector dipole strength distribution [33, 34].

Successful description of the IVDGRs within the RMT approach in the lead region suggests to describe the GMR in the same vein. To demonstrate the validity of our approach we shall compare the results of: (i) the microscopic calculations, based on the coupling between one-phonon and two-phonon configurations, so called phonon–phonon coupling (PPC); (ii) the random matrix approach based on the one-phonon approximation; and (iii) available experimental data for ^204,206,208Pb nuclei. To this aim we employ the modern development of the quasiparticle–phonon model, where the single-particle spectrum and the residual interaction are determined making use of the Skyrme interaction without any further adjustments [35].

Hereafter, we use the parameter set of SLy4 [36, 37], which is adjusted to reproduce the nuclear matter properties, as well as nuclei charge radii, binding energies of doubly magic nuclei. The pairing correlations are generated by a zero-range volume force. The pairing constant is taken as –280 MeV fm³ [33]. In order to limit the pairing single-particle space, we have used the smooth cutoff at 10 MeV above the Fermi energies [38]. Below, for a self-contained discussion of our approach developed in Section 3, the main features of the PPC approach and the doorway model based on the RMT ideas will be overviewed briefly.

Phonon–Phonon Coupling Model

By means of the finite rank separable approximation [39, 38] for the residual interaction we perform the QRPA calculations in very large two-quasiparticle spaces. The cutoff of the discretized continuous part of the single-particle spectra is taken at the energy of 100 MeV. This is sufficient to exhaust practically all the sum rules [40, 24]. The QRPA solutions are treated as quasi-bosons with quantum numbers ${{\lambda }^{\pi }}$. Among these solutions there are one-phonon states ${{\omega }_{{\lambda i}}}$ corresponding to collective GRs and pure two-quasiparticle states.

To construct wave functions of the excited 0⁺ states up to 20 MeV we take into account all two-phonon terms that are built from the phonons of different multipolarities ${{\lambda }^{\pi }}{{ = 0}^{ + }}{{,1}^{ - }}{{,2}^{ + }}{{,3}^{ - }}{{,4}^{ + }}$, coupled to 0⁺ state. In other words, we build two-phonon configurations that consist of the phonon compositions ${{[\lambda _{i}^{\pi } \otimes \lambda _{j}^{\pi }]}_{{{{\lambda }^{\pi }}{{{ = 0}}^{ + }}}}}$ (see details in [10, 24, 41]). Following the basic ideas of the quasiparticle–phonon model [5], the Hamiltonian is then diagonalized in a space spanned by states composed of one and two phonons coupled by means of the microscopic coupling matrix elements (see details in [35, 42]). The diagonalization results in eigenstates ${\text{|}}0_{\nu }^{ + }\rangle$ with corresponding energies ${{\omega }_{\nu }}$.

The basic steps of the calculations of the strength distribution of the GMR, $b(E0,E)$, in the PPC approach for ²⁰⁸Pb are discussed in [41]. In brief, we define the strength distribution as

$$b(E0,E) = \sum\limits_\nu {\text{|}}\langle 0_{\nu }^{ + }{\text{|}}{{\hat {M}}_{{\lambda {{{ = 0}}^{ + }}}}}{\text{|}}{{0}^{ + }}\rangle {{{\text{|}}}^{2}}\rho (E - {{E}_{\nu }}),$$

(1)

where ${\text{|}}\langle 0_{\nu }^{ + }{\text{|}}{{\hat {M}}_{{\lambda {{{ = 0}}^{ + }}}}}{\text{|}}{{0}^{ + }}\rangle {{{\text{|}}}^{2}}$ is the transition probability from the ground state ${\text{|}}{{0}^{ + }}\rangle$ to the excited state ${\text{|}}0_{\nu }^{ + }\rangle$. The transition operator of the GMR is defined as

$${{\hat {M}}_{{\lambda {{{ = 0}}^{ + }}}}} = \sum\limits_{i = 1}^A r_{i}^{2}{\kern 1pt} .$$

(2)

The strength distribution is described with the aid of the Lorentzian function

$$\rho (\omega - {{\omega }_{\nu }}) = \frac{1}{{2\pi }}\frac{\Delta }{{{{{(\omega - {{\omega }_{\nu }})}}^{2}} + {{\Delta }^{2}}{\text{/}}4}},$$

(3)

with $\Delta = 1$ MeV.

The QRPA analysis provides the location of the GMR in ^204,206,208Pb in the energy region ${{E}_{x}} = 8{-} 20$ MeV. In particular, in nucleus ²⁰⁸Pb there is one, strongly dominating peak in the strength distribution at 14.6 MeV (see Fig. 1). The PPC yields a detectable redistribution of the GMR strength in comparison with the RPA results. It results in the 1 MeV downward shift of the main peak. Our analysis shows that the major contribution to the strength distribution is brought about by the coupling between the ${{{{[0}^{ + }}]}_{{RPA}}}$ and ${{{{[3}^{ - }} \otimes {{3}^{ - }}]}_{{RPA}}}$ components [41].

Fig. 1.

(Color online) $E0$ strength function, $b(E0,E)$, for ²⁰⁸Pb as a function of energy. The dotted (black) line connects the RPA results, and the solid (blue) line connects the PPC results. The random matrix approach on one energy scale is applied for three values of the coupling strengths, $\sigma = 30$ (red dashed line), 60 (red dot-dashed line), and 90 keV (red solid line).

Random Matrix Theory Approach

Let us recapitulate the basic steps of the statistical description of the GMR fragmentation based on ideas from the RMT [33, 34]. In our approach the one-phonon states are generated by means of the QRPA calculations, while the coupling matrix elements between the one- and two-phonon states are replaced by random matrix elements of the GOE-type. Namely, we consider a doorway Hamiltonian

$${{H}_{{{{\lambda }^{\pi }}}}} = {{H}_{d}} + {{H}_{b}} + V,$$

(4)

where the Hamiltonian ${{H}_{d}} = \sum\nolimits_i^{{{N}_{d}}} {{{\omega }_{i}}Q_{i}^{ + }{{Q}_{i}}}$ is characterized by energies ${{\omega }_{i}}$ obtained from the microscopic calculations of the monopole phonon states, and the N_d one-phonon states constitute the doorway states. The background states ${{N}_{b}}$ are two-phonon and possibly more complex states, are eigenstates of the Hamiltonian ${{H}_{b}} = \sum\nolimits_k^{{{N}_{b}}} {{{\Omega }_{k}}a_{k}^{ + }{{a}_{k}}}$ with eigenstates ${\text{|}}b;{{\Omega }_{k}}\rangle$ and corresponding energies ${{\Omega }_{k}}$. The number of background states is much larger than the number of doorway states, ${{N}_{b}} \gg {{N}_{d}}$.

We recall that the Hamiltonian ${{H}_{{{{\lambda }^{\pi }}}}}$ represents a set of good quantum numbers, ${{\lambda }^{\pi }}$, and the QRPA phonons as well as all background states fulfill these quantum numbers. We assume no coupling between different doorway states or between different background states, $\langle d{\text{|}}V{\text{|}}d'\rangle = 0$ and $\langle b{\text{|}}V{\text{|}}b'\rangle = 0$, but all coupling takes place between the doorway states and the complex background states, $\langle d{\text{|}}V{\text{|}}b\rangle$ = ${{V}_{{db}}} \Rightarrow {{V}_{{{{d}_{i}},{{b}_{k}}}}}$ = $\langle d;{{\omega }_{i}}{\text{|}}V{\text{|}}b;{{\Omega }_{k}}\rangle$. As discussed above, the microscopic coupling (PPC) matrix elements are replaced by a random interaction where the matrix elements ${{V}_{{{{d}_{i}},{{b}_{k}}}}}$ are Gaussian distributed random numbers,

$$P({{V}_{{{{d}_{i}},{{b}_{k}}}}}) = \frac{1}{{\sigma \sqrt {2\pi } }}\exp \left( {\frac{{ - V_{{{{d}_{i}},{{b}_{k}}}}^{2}}}{{2{{\sigma }^{2}}}}} \right),$$

(5)

with the width or strength $\sigma = \sqrt {\langle V_{{{{d}_{i}},{{b}_{k}}}}^{2}\rangle }$ and fulfilling ${{V}_{{{{d}_{i}},{{b}_{k}}}}} = {{V}_{{{{b}_{k}},{{d}_{i}}}}}$. The one-phonon states are thus considered as doorway states to the fragmentation of E0‑strength on background states.

Thus, our aim is to describe microscopically the one-phonon GMRs states, and attempt a random matrix inspired treatment of the coupling to complex surrounding states, here viewed as two-phonon states. The quality of the random treatment can then be studied by comparing results with the microscopic PPC model predictions. The use of the random matrix distribution yields the backshifting of the main peak. In fact, with increasing the coupling strength $\sigma = 30$, 60, and 90 keV the peak of the strength distribution of monopole excitations is gradually pushed down in strength in case of ²⁰⁸Pb (see Fig. 1). At the same time the peak is pushed down to lower excitation energies. Note, in this case there is only an average strength that does not produce any preferences in the coupling between one- and two-phonon states of different one-phonon nature. There seems to be no way to come close to the PPC result in the RMT model for any coupling strength. The reason for this is that the density of two-phonon states increases with excitation energy, as ${{\rho }_{{2 - {\text{ph}}}}} \propto {{E}^{3}}$ [34]. With a random Gaussian distributed coupling between the one-phonon and the two-phonon states, the number of two-phonon states with high energies are much larger than the number of the matrix elements coupled to low two-phonon energies. Consequently, the increase of the repulsion (the coupling strength σ) between the one- and two-phonon states pushes the main peak of the strength function down in energy, while the high-lying tail appears as well. This picture deviates more and more from the PPC result as the coupling strength σ is increased.

RANDOM MATRIX THEORY ON DIFFERENT ENERGY SCALES

In order to resolve the arising problem we turn to the successful attempts to understand the fine structure of the ISQGR with the aid of the wavelet analysis [21]. In the heart of this analysis there is the idea on presence of different energy scales, responsible for fluctuations of the cross section of any resonance (see also analysis within simple models in [16, 19]). The essence of the analysis [21] guides us to suppose that it would be useful to study the decomposition of the full model space on different subspaces, responsible for different decay mechanisms. In practical terms it means the separation of the coupling matrix elements on two classes: (i) the coupling matrix elements responsible for the strong coupling between low-lying vibrations and the doorway states; (ii) the coupling matrix elements between the doorway states and large background of incoherent states.

To illuminate this suggestion we consider the distribution of microscopic coupling matrix elements ${{W}_{{i,j}}}$ (calculated in the PPC approach) for ²⁰⁶Pb, taken as a typical example (see Fig. 2). The distribution of all coupling matrix elements is well reproduced by a (truncated) Cauchy distribution. We recall that stable distributions, such as the Cauchy distribution, have long tails and infinite variance. However, considering truncated Cauchy distributions, according to the central limit theorem, the resulting shape (the average of the sum) is driving the Gaussian distribution. Indeed, the distribution of the bulk of coupling matrix elements (basically, small in value) follow approximately the Gaussian distribution. While large coupling matrix elements are distributed on irregular tails. In the energy interval 8–20 MeV the number of one-phonon QRPA states are 27, 28, and 15, while the number of two-phonon states coupled to 0⁺ are 2126, 2210, and 914 for ²⁰⁴Pb, ²⁰⁶Pb, and ²⁰⁸Pb, respectively. The rms-value of the many matrix elements corresponding to the Gaussian distribution (the central part in Fig. 2) is approximately ${{\sigma }_{2}} \approx 30$ keV for ^204,206,208Pb, which we shall use in the random matrix approach (see below).

Fig. 2.

(Color online) Distribution of the coupling matrix elements between monopole one- and two-phonon QRPA states. The probabilities $P({{W}_{{i,j}}})$ are shown on log scale for ²⁰⁶Pb (black solid line). A fit to a Cauchy distribution is shown by red dashed line. The Gaussian distribution of the matrix elements, used for the weak coupling with ${{\sigma }_{2}} =$ 30 keV, is shown by a dot-dashed line.

Taking the above analysis into account, we model the random matrix Hamiltonian in the following way:

$$\hat {H} = {{\hat {H}}_{0}} + {{\hat {H}}_{1}} + {{\hat {H}}_{2}}.$$

(6)

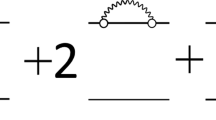
Here, the term ${{\hat {H}}_{0}}$ describes doorway states. These states are associated with the 0⁺ one-phonon states calculated within the QRPA. The two-phonon Hamiltonians are

$${{\hat {H}}_{k}} = {{\hat {H}}_{{k0}}} + {{\hat {V}}_{k}},\quad k = 1,2,$$

(7)

where ${{\hat {H}}_{{k0}}}$ describes two-phonon states that consist of the phonon compositions as ${{[\lambda _{i}^{\pi } \otimes \lambda _{j}^{\pi }]}_{{{{\lambda }^{\pi }}{{{ = 0}}^{ + }}}}}$, with en-ergies ${{E}_{{ij}}} = E({{\lambda }_{i}}) + E({{\lambda }_{j}})$, built by means of one- phonon states with ${{\lambda }^{\pi }}{{ = 0}^{ + }}$, 1^–, 2⁺, 3^–, and 4⁺. The term ${{\hat {H}}_{{10}}}({{\hat {H}}_{{20}}})$ is coupled strongly (weakly) to the one-phonon states by means of the random force ${{\hat {V}}_{{1(2)}}}$. In this case the strong (weak) coupling matrix elements are Gaussian random variables with zero mean value and a second moment $\sigma _{1}^{2}(\sigma _{2}^{2})$ between the doorway states and the background states. The two-phonon states that belong to the term ${{\hat {H}}_{{10}}}$ have a low-level density, typically 1 state per MeV. The states that belong to the term ${{\hat {H}}_{{20}}}$ correspond to the rest of the two-phonon states. The matrix representation of the discussed Hamiltonian is displayed on Fig. 3.

Fig. 3.

(Color online) Schematic view of the random matrix Hamiltonian on two energy scales. First submatrix describes the one-phonon QRPA states with energies ${{E}_{i}}{{(0}^{ + }})$. Middle submatrix is associated with the two-phonon states with energies ${{E}_{{i,j}}}$ that are strongly coupled to the one-phonon states with the random coupling ${{V}_{1}}$. Third submatrix is associated with the two-phonon states with energies ${{E}_{{k,l}}}$ that are weakly coupled to the one-phonon states with the random coupling ${{V}_{2}}$. There is no coupling between one-phonon states, or between two-phonon states. Only one- and two-phonon states are coupled.

At this point there are a few comments in order. Thus, we have to determine the main principle how to select the strongest coupling matrix elements for our random matrix approach. To this aim we propose the procedure without performing the full PPC calculations, where the matrix elements actually are calculated. The QRPA provides the energy and the electric transition matrix element of the one-phonon state, corresponding to a given multipolarity ${{\lambda }^{\pi }}$, to the ground state ${\text{|}}{{0}^{ + }}\rangle$, i.e., $B(E\lambda ) \propto {\text{|}}\langle {{\omega }_{{{{\lambda }^{\pi }}}}}{\text{|}}\hat {E}(\lambda ){\text{|}}{{0}^{ + }}\rangle {{{\text{|}}}^{2}}$. Evidently, the most collective vibrations (phonons) of different multipolarity are of main interest for us. Therefore, the electric transition matrix element of each phonon state is subsequently transformed to Weisskopf single-particle units, ${{B}_{{s.p.}}}{{(\lambda )}_{i}}$ by dividing the calculated transition strength by the Weisskopf estimate [12] for transition from the ground state 0⁺ to the excited states ${{\lambda }^{\pi }}$. On the other hand, keeping in mind the fact that two-phonon states are formed from the tensor product of identical multipole operators counted at different energies, we consider the joint product of their transition probabilities to the ground state ${{M}_{{i,j}}} = {{B}_{{s.p.}}}{{(E\lambda )}_{i}}{{B}_{{s.p.}}}{{(E\lambda )}_{j}}$.

In Table 1 the ten largest microscopic coupling matrix elements, obtained by means of the PPC approach, are compared with the $M$-values for the corresponding two-phonon compositions in the case of ²⁰⁸Pb. It can be seen that the selection of the two-phonon states with the largest M-values is in fair agreement with the largest values of ${\text{|}}{{W}_{{i,j}}}{\text{|}}$. Out of the two-phonon states with the ten strongest matrix elements, nine are found by this simplified rule. The only exception is the two-phonon state with $E = 16.1$ MeV, which is built on the connection of the first $3_{1}^{ - }$ vibration with the pure two-quasiparticle $3_{{41}}^{ - }$ state. Additionally, two-phonon states with two 0⁺ RPA phonons, coupled to 0⁺, appear to have very small coupling matrix elements with the one-phonon 0⁺ RPA phonons, and are neglected in this process. The reason why the two-phonon states with two 0⁺ phonons give a small coupling to the one-phonon 0⁺ state is a geometrical factor, as described in Appendix B of [35].

Table 1. Characteristics of ten largest matrix elements between a two-phonon state coupled to ${{\lambda }^{\pi }}{{ = 0}^{ + }}$, and the one-phonon RPA 0⁺ state at 14.6 MeV carrying the strongest monopole transition strength to the ground state in ²⁰⁸Pb. First column: the configuration of the two-phonon states is given in terms of two coupled QRPA phonons. Second column: the corresponding energies. Third column: the corresponding PPC matrix elements. Fourth column: the product of transition matrix elements, ${{M}_{{i,j}}}$, in terms of single-particle Weisskopf units (see text)

The ten energies, shown in Table 1, are evenly distributed over the considered energy interval with about one state per MeV, and the rms-strength of the PPC calculated coupling matrix elements is ${{\sigma }_{1}} = 588$ keV. Similar results are obtained for ^204,206Pb with the rms values of the ten strongest matrix elements ${{\sigma }_{1}} = 560$, 590 keV, respectively. Thus, given these results, we shall consider the group of strongly coupled matrix elements with the coupling strength ${{\sigma }_{1}} \approx 600$ keV and with the density ${{\rho }_{1}} = 1$ MeV^–1.

Figure 4 shows the strength distributions of monopole excitations for different values of the random coupling matrix elements strength ${{\sigma }_{1}}$ between the subspace of two-phonon states and the one-phonon GMR state. These strength distributions are obtained by ensemble averaging over 100 realizations. Each realization is calculated with the aid of the coupling matrix elements randomly generated by means of the Gaussian distribution (5). We recall that Eq. (5) approximates (according to the central limit theorem) the resulting shape (the average of the sum) random generations of the coupling matrix elements for each considered value ${{\sigma }_{1}}$. If the weak part of the interaction is neglected in the RMT model (${{\sigma }_{2}} = 0$), the strength function is gradually broadened as the strong interaction (${{\sigma }_{1}}$) is increased (see Fig. 4). Switching on the strong as well as the week interactions, with the chosen values ${{\sigma }_{1}} = 600$ keV and ${{\sigma }_{2}} = 30$ keV, the RMT results are in a quite good agreement with those of the PPC (see Fig. 5). It is notable that the strength distribution of the GMR, obtained in this case, is rather close to the experimental distribution [43].

Fig. 4.

(Color online) Monopole transition strength $b(E0,E)$ versus the transition energy $E$ in the case of ²⁰⁶Pb. The results are shown for different values of the strong coupling strength, ${{\sigma }_{1}}$, assuming the week coupling strength ${{\sigma }_{2}} = 0$. For a comparison the result, obtained by means of the PPC theory, is shown by blue solid line.

Fig. 5.

(Color online) Monopole transition strength $b(E0,E)$ versus the transition energy $E$ in the case of ²⁰⁶Pb. The results, obtained by means of: (i) the two-scale RMT approach are connected by (red) solid line; (ii) the microscopic PPC calculations are connected by (blue) dashed line; (iii) the QRPA approach are connected by (black) dotted line. For a comparison the experimental data [43] shown by (black) squares with error bars, smoothly interpolated, are connected by (black) thin line.

The experimental and calculated positions of the energy centroids, E_c and the width of the GMRs for the three considered lead isotopes are shown in Table 2. The values of E_c and $\Gamma$ have been computed in the energy region 10.5–18.5 MeV and defined by means of the energy-weighted moments ${{m}_{k}} = \int b(E0,E){\kern 1pt} {{E}^{k}}{\kern 1pt} dE$: (i) ${{E}_{{\text{c}}}}\, = \,{{m}_{1}}{\text{/}}{{m}_{0}}$; (ii) $\Gamma = 2.35\sqrt {{{m}_{2}}{\text{/}}{{m}_{0}} - {{{\left( {{{m}_{1}}{\text{/}}{{m}_{0}}} \right)}}^{2}}}$. Applying the RMT approach, based on two energy scales, to the calculation of the monopole strength distribution for ^204,208Pb, we obtain quite satisfactory agreement with the experimental data [43]. On the other hand, the agreement between the results of the microscopic PPC and the RMT calculations of the monopole strength distribution (see Figs. 5–7) is quite remarkable.

Table 2. Lorentzian fits of measured [43] and calculated in the RMT, PPC approaches the values of centroid energy ${{E}_{{\text{c}}}}$ and width $\Gamma$ of $E0$ strength function $b(E0,E)$, shown in Figs. 5–7. The values of ${{E}_{{\text{c}}}}$ and $\Gamma$ have been computed in the energy region 10.5–18.5 MeV

Fig. 6.

(Color online) Same as in Fig. 5 but for ²⁰⁴Pb.

Fig. 7.

(Color online) Same as in Fig. 5 but for ²⁰⁸Pb. The RMT results are connected by dashed (red) line, while the PPC results are connected by solid (blue) line.

SUMMARY

In this paper we have suggested the effective approach for description of the GMR spreading width. It is shown that this description can be successfully fulfilled by means of the microscopic calculations of the QRPA states alone, that are mixed by means of the coupling matrix elements with two-phonon states, generated with the aid of the GOE distribution.

Within the framework of our approach the two-phonon model space is decomposed on two subspaces that are differently coupled to the QRPA states. We have demonstrated that two energy scales, corresponding to large and small coupling strengths of two-phonon states to one-phonon states, provide a better description naturally, accounting for fine structure effects. On the larger energy scale the gross structure and structure effects of the GMRs are defined; that includes the random coupling to surface vibrations of a few strongest coupling matrix elements. The weaker coupling on a smaller energy scale is also important, and is particularly responsible for the fine structure of the strength function in the energy region around the GMR. Similar studies were performed in [21] for the ISQGRs, where the characteristic scales have been discussed, motivated from a wavelet analysis of the measured strength functions. In contrast to the latter case, we provided the recipe of the selection of the most important coupling matrix elements that determine the large scale of the strength (see Section III).

To illustrate the quality of our approach, all numerical calculations have been done on the basis of the Skyrme forces SLy4. Our major goal was to elucidate the efficiency of the proposed approach than rather to reproduce with the high accuracy experimental data by selecting, for example, the specific Skyrme functional (e.g., [29]). Consequently, our attempts were aimed to obtain a better understanding of the gross structure of the resonance and, basically, to reproduce the microscopic PPC result by modest means. The remarkable agreement between the results of the PPC and the RMT calculations for the GMR strength distribution of ^204,206,208Pb confirms the vitality and validity of our approach. Noteworthy is the fact that our approach can be readily extended with the proposition of the mixing with three-phonon states. While it is a laborious task in microscopic calculations.