1 INTRODUCTION

In the past decade, a great deal of effort was mounted in low-energy theoretical nuclear physics on developing a unified description of properties of both ground and excited states of nuclei up to energies in the range between 30 and 35 MeV [2–6]—first of all, the properties of pygmy dipole and giant multipole resonances (PDR and GMR, respectively). A dominant trend in the development along these lines consisted in applying and evolving self-consistent approaches based on the use of energy density functionals. This made it possible to obtain unified and, by and large, quite successful descriptions of the aforementioned properties in terms of a moderately small number of parameters (for an overview, see [3–5]). However, a vigorous development of the experimental base in these realms [4, 7, 8], especially in the energy region of the pygmy dipole resonance, ever brings about new questions to the respective microscopic theory [3, 9]. For example, the upbend of the radiative strength function in the range between 1 and 3 MeV [8] calls for an explanation. The problem of describing the fine structure of pygmy dipole and giant multipole resonances [7] is worthy of special note, since, in this problem, any details of the theory that lead to the redistribution of the strength are of importance [10, 11].

From the physics point of view, this problem is understandable but only in principle—it is necessary to take reliably into account coupling to phonons, or quasiparticle–phonon interaction, in addition to standard methods of the random-phase approximation (RPA) and quasiparticle random-phase approximation (QRPA). This problem was discussed in detail in the theory, but there is a large room for improvements of the existing approaches. We believe that the development within a consistent quantum many-body formalism, primarily within the method of quantum Green’s functions, on the basis of extending the self-consistent Theory of Finite Fermi Systems (TFFS) [12–14] is a very promising approach. This is a general purpose of our present study and, possibly, several future studies.

In the region of a self-consistent description of the properties of the ground state and several low-lying collective states, a large amount of work was performed by physicists from Kurchatov Institute, so that it can be said that the second step in the development of TFFS methods was made [5, 15, 16]. There, use was made primarily of the method of an effective density functional involving the Fayans parameters [15]. In all of the numerous problems considered in those studies, the role of quasiparticle–phonon interaction was found to be quite significant and to be crucial for explaining experimental data. In the opinion of the present authors, those studies owed their success to the use of the quantum method of many-body theory—more precisely, the Green’s function method.

Simultaneously, the Green’s function method was used to describe the pygmy dipole and giant multipole resonances both within non-self-consistent [6, 17, 18] and self-consistent [19, 20] approaches. The difference between the methods used in [17] and in [18] was that, in [18], the drawback of the method applied in [17] was removed—namely, an approximate method of a chronological decoupling of diagrams (MCDD), or (in more modern terms) the time-blocking approximation (TBA), was proposed. The aforementioned drawback was immaterial for explaining the properties of the \(\text{M}\)1 resonance, which lies in the energy region of the pygmy dipole resonance [21, 22]. Moreover, the respective approach was in fact applied earlier within Nuclear Field Theory and in describing electric giant multipole resonances [23, 24] with the use of an averaging parameter of 600 keV. More recently, the method was substantially modified and, for problems in nuclei that involve pairing, was called the quasiparticle time-blocking approximation (QTBA) [25–27]. However, the main physics content of the method—that is, the inclusion of quasiparticle–phonon interaction only in the particle–hole propagator (in terms of TFFS)—remained unchanged, even though the derivation relied on an alternative approach based on the Bethe–Salpeter equation.

A new approach in the theory of pygmy dipole and giant multipole resonances was considered in [1]. This approach was based on a consistent inclusion of effects of quasiparticle–phonon interaction in the TFFS framework with the aim of extending this theory to the energy region of pygmy dipole and giant multipole resonances in magic nuclei. Only complex configurations involving phonons and belonging to the \(1p1h\otimes\textrm{phonon}\) type were taken into account in that study. Despite the limitations of this approach—for example, the absence of two-phonon configurations (see [28])—it turned out to be possible to obtain a number of new effects, such as the dynamical tadpole effect, phonon-exchange effective interaction mediated by the exchange of phonons in various channels, and the first and second variations of the effective interaction in the phonon field. In [1], use was made of a substantial assumption for the first, \(\delta^{(1)}V\), and second, \(\delta^{(2)}V\), variations of the vertex in the phonon field—namely, only free terms in the equations for these variations of the vertex were taken into account. This approximation led to taking into account only complex configurations of the \(1p1h\otimes\textrm{phonon}\) type. In the present study, we go beyond this approximation, obtaining and employing exact expressions for \(\delta^{(1)}V\) and \(\delta^{(2)}V\) and deriving, with the aid of them, new equations for the vertex.

In a sense, a somewhat unexpected result was obtained in [1]. Owing to one of the two \(g^{2}\) corrections to the vertex that were used—specifically, the correction containing the phonon-production amplitude \(g\)—the new vertex was dependent on the energy variable \(\varepsilon_{1}\) off the mass shell, \(\varepsilon_{1}=\varepsilon_{\lambda_{1}}\). This dependence is of interest in itself and does not appear in the main observables—transition energies and probabilities. However, it seems reasonable to simplify the problem and to study a model where there is no such dependence. Herein lies a ‘‘model character’’ of our model—that is, the use of only one correction (of greatest importance!) to the vertex. We will see that this approach makes it possible to clarify the situation concerning the inclusion of quasiparticle–phonon interaction, at least within the broad range of extensions of the standard TFFS framework.

In the present study, we consider only the \(1p1h\otimes\textrm{phonon}\) and two-phonon configurations in magic nuclei. As usual, we use the existence of the small parameter \(g^{2}\). Very often, we give a symbolic form of our formulas, which are mostly representable in terms of Feynman diagrams, so that one can readily reconstruct their final form.

2 SOME RESULTS OF THE SELF-CONSISTENT THEORY OF FINITE FERMI SYSTEMS

Within the standard TFFS framework, the effective field (vertex) \(V\), which describes the nuclear polarizability, is the main quantity in problems associated with the interaction of a nucleus with an external field \(V^{0}(\omega)\) of energy \(\omega\). The equation for this effective field has the symbolic form [12]

$$V=e_{q}V^{0}+FAV,$$
(1)

where

$$A_{12}(\omega)=\int G_{1}(\varepsilon)G_{2}(\varepsilon-\omega)d\varepsilon.$$
(2)

The total particle–hole interaction amplitude \(\Gamma\) satisfies the equation

$$\Gamma=F+FA\Gamma.$$
(3)

Within the TFFS framework, the phonon-production amplitude \(g\) satisfies the homogeneous equation (in a symbolic form) [12]

$$g=FAg.$$
(4)

In Eqs. (1), (3), and (4), \(F\) is the effective Landau–Migdal interaction, which, in the self-consistent theory of finite Fermi systems [15], is specified as the second variational derivative of the energy density functional, while \(A\) is the particle–hole propagator, which is an integral of two Green’s functions. These equations correspond to the ordinary RPA approach for magic nuclei, which is formulated in terms of Green’s functions. The subscripts stand for the set of single-particle quantum numbers: 1\(\equiv(n_{1},j_{1},l_{1},m_{1})\equiv\lambda_{1}\).

In [13, 29, 30], a quantity that we called a phonon tadpole [31] was introduced. In general, it is the variation of the amplitude \(g_{1}\) for the production of a phonon with angular momentum \(L_{1}\) in the field \(g_{2}\) of another phonon with angular momentum \(L_{2}\), but, by definition, the quantity \(g_{12}\) with \(L_{1}=L_{2}=L\) appears in the phonon tadpole. The amplitude \(g_{12}\) for the production of two phonons satisfies the equation that can be obtained as the variation of Eq. (4) for the amplitude \(g_{1}\) for the production of one phonon in the field \(g_{2}\) of another phonon; that is,

$$g_{12}=\delta_{1}FAg_{2}+F(\delta_{1}A)g_{2}+FAg_{12},$$
(5)

where

$$\delta_{1}A=Gg_{1}GG+GGg_{1}G.$$
(6)

Equation (5) is an integral equation involving two free terms. This equation was solved only in the coordinate representation in the aforementioned studies of the physicists from Kurchatov Institute. In their remaining studies, they used a realistic estimate for the two-phonon production amplitude \(g_{11}\), which determines the phonon tadpole. The estimate in question was based on the following ansatz for the quantity \(\delta_{1}F\equiv\delta F\) appearing in Eq. (5):

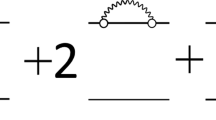
$$\delta F=\left(\frac{\delta F}{\delta\rho}\right)Ag.$$
(7)

As was mentioned in the Introduction, the physics content of the previous studies that relied on the Green’s function method was that the authors included the \(g^{2}\) correction only in the particle–hole propagator (2). In TFFS terms, this means that the equation of the diagrammatic form in Fig. 1 for the vertex \(V^{\prime}\) was solved. Physically, this also corresponds to the approach within Nuclear Field Theory [23, 24] for giant multipole resonances. Hereafter, the digit 2 in front of a graph or the corresponding expression means that there are two graphs or expressions of a similar type. In order to obtain a more accurate description, it is necessary to use the recipe that was proposed in [18] for improving this approach [that is, MCDD or TBA] and which is based on the introduction of the Heaviside step function in the respective equation. The generalized MCDD propagator is of a rather complicated form. It is described in detail elsewhere [6].

Fig. 1
figure 1

Equation for the vertex \(V^{\prime}\) with allowance for the simplest propagator involving quasiparticle-phonon interaction [17, 21]. Straight and wavy lines represent the Green’s functions \(G\) and \(D\), respectively; open circles with one wavy line stand for the phonon-production amplitude \(g\); and rectangles correspond to the effective interaction \(F\).

Full size image

In Fig. 1, the diagrams without phonons correspond to the RPA approach formulated in terms of the standard theory of finite Fermi systems—that is, to Eq. (1) with the propagator in (2).

3 EXACT EXPRESSIONS FOR THE FIRST AND SECOND VARIATIONS OF THE VERTEX, \(\delta^{(1)}V\) AND \(\delta^{(2)}V\)

In order to obtain the \(g^{2}\) correction to the vertex \(V\) (1), we use, as was done in [1], the expression

$$\tilde{V}=V+\Delta V(g,V),$$
(8)

where, according to our model,

$$\Delta V=\delta^{(2)}VD.$$
(9)

Here, \(\delta^{(2)}V\) is the second-order variation of the vertex \(V\) (1) in the phonon field. It is shown in Fig. 2.

Fig. 2
figure 2

Diagrammatic representation of the \(g^{2}\) correction (9) to the vertex \(V\) (1).

Full size image

First of all, we obtain the quantity \(\delta^{(2)}A\) for our case of identical phonons in \(\delta^{(2)}V\). In order to avoid confusion of the phonon index in \(g\) with the single-particle indices, we introduce here the notation \(\tilde{1}\) for phonons. In our case, we have \(\tilde{1}=\tilde{2}\) (Fig. 2), which corresponds to \(\delta^{(2)}V=\delta^{\tilde{1}}\delta^{\tilde{1}}V\). Varying the quantity \(\delta^{(2)}A\), we obtain five terms shown in Fig. 3: that is,

Fig. 3
figure 3

Diagrammatic representation of expression (10).

Full size image
$$\delta^{(2)}A=\delta^{\tilde{1}}\delta^{\tilde{1}}G_{1}G_{2}=2G_{1}g_{\tilde{1}}G_{4}g_{\tilde{1}}G_{3}G_{2}$$
(10)
$${}+2G_{1}g_{\tilde{1}\tilde{1}}G_{3}G_{2}+G_{1}g_{\tilde{1}}G_{3}G_{2}g_{\tilde{1}}G_{4}.$$

Even from here, one can see that the graph at the center corresponds to the future tadpole effect, which is absent in Fig. 1.

The quantities \(\delta^{(1)}V\) and \(\delta^{(2)}V\) are obtained by varying Eq.(1) in the phonon field [1];that is,

$$\delta^{(1)}V=\delta^{(1)}FAV+F\delta^{(1)}AV+FA\delta^{(1)}V,$$
(11)
$$\delta^{(2)}V=\delta^{(1)}\delta^{(1)}V=F\delta^{(2)}AV$$
$${}+2\delta^{(1)}F\delta^{(1)}AV+2\delta^{(1)}FA\delta^{(1)}V$$
$${}+2F\delta^{(1)}A\delta^{(1)}V+\delta^{(2)}FAV+FA\delta^{(2)}V.$$

In [1], the quantities \(\delta^{(1)}V\) and \(\delta^{(2)}V\) were taken into account approximately—that is, only the free terms in Eq. (11) were considered. This approximation led to taking into account the only configurations of the \(1p1h\otimes\textrm{phonon}\) type.

In this study, we do not use this approximation and transform Eq. (11) to exact expressions for \(\delta^{(1)}V\) and \(\delta^{(2)}V\).

We recast Eg. (11) for \(\delta^{(1)}V\) and \(\delta^{(2)}V\) into the form (symbolically, as usual)

$$(1-FA)\delta^{(1)}V=(\delta^{(1)}V)_{0},$$
(12)
$$(1-FA)\delta^{(2)}V=(\delta^{(2)}V)_{0},$$

where \((\delta^{(1)}V)_{0}\) and \((\delta^{(2)}V)_{0}\) are the free terms of Eq. (11). Its alternative form is

$$\delta^{(1)}V=(1-FA)^{-1}(\delta^{(1)}V)_{0},$$
(13)
$$\delta^{(2)}V=(1-FA)^{-1}(\delta^{(2)}V)_{0}.$$

Following [30], we introduce \(d\Gamma\) (in order to avoid confusion with the ordinary variation for \(\Gamma\) in (3), we used this notation instead of \(\delta\Gamma\) in [30]):

$$d\Gamma=\delta^{(1)}F+FAd\Gamma.$$
(14)

Below, we employ the following symbolic expressions obtained from Eqs. (3) and (14):

$$\Gamma=(1-FA)^{-1}F,$$
(15)
$$d\Gamma=(1-FA)^{-1}\delta^{(1)}F.$$

Substituting the free terms \((\delta^{(1)}V)_{0}\) and \((\delta^{(2)}V)_{0}\) of Eqs. (11) into (13) and employing Eq. (15), we obtain exact expressions for \(\delta^{(1)}V\) and \(\delta^{(2)}V\) in the form

$$\delta^{(1)}V=d\Gamma AV+\Gamma\delta AV,$$
(16)
$$\delta^{(2)}V=\Gamma\delta^{(2)}AV+2d\Gamma\delta AV+2d\Gamma A\delta^{(1)}V+$$
$$2\Gamma\delta A\delta^{(1)}V+d^{(2)}\Gamma AV.$$

They already contain \(\Gamma\) and \(d\Gamma\) instead of \(F\) and \(\delta F\). We introduce the quantity

$$d^{(2)}\Gamma=\delta^{(2)}F+FAd^{(2)}\Gamma,$$
(17)

or

$$d^{(2)}\Gamma=(1-FA)^{-1}\delta^{(2)}F.$$
(18)

The exact expressions obtained for \(\delta^{(1)}V\) and \(\delta^{(2)}V\) are shown in Fig. 4.

Fig. 4
figure 4

Exact expressions for the first and second variations \(\delta^{(1)}V\) and \(\delta^{(2)}V\) of the vertex V in the phonon field. The rectangles with \(\Gamma\), \(d\Gamma\), and \(d^{(2)}\Gamma\) stand for, respectively, \(\Gamma\) (4), \(d\Gamma\) (14), and \(d^{(2)}\Gamma\) (17).

Full size image

It is noteworthy that the expressions for \(\delta^{(1)}V\) and \(\delta^{(2)}V\) are ‘‘exact’’ in the sense that they involve precisely the quantities that are inherent in the theory of finite Fermi systems: for the vertex \(V\) in Eq. (1), these are the amplitudes \(\Gamma\) (3), the phonon-production amplitudes \(g\) (4), and \(d\Gamma\) (14). In this sense, everything complies here with the original TFFS ideas [12]. A fundamental distinction from what we have in [1] is that below, we use the exact expressions (16) for \(\delta^{(1)}V\) and \(\delta^{(2)}V\), Fig. 4, instead of the free terms of Eqs. (11) for them. Expressions (16), Fig. 4, are the first main result of our present study.

4 NEW EQUATION FOR THE EFFECTIVE FIELD

4.1 \(1p1h\otimes\textrm{phonon}\) Configurations and Total Interaction Amplitude \(\Gamma\)

Let us consider our original formula (8) for the vertex. One can readily see that expression (8) is the first iteration of the equation (if \(V\) in Eq. (1) is the zero-order iteration); that is

$$\tilde{V}=V+\Delta V(g,\tilde{V}),$$
(19)

where \(\Delta V(g,\tilde{V})\) already contains the new vertex \(\tilde{V}\) in the quantities \(\delta^{(1)}V\) and \(\delta^{(2)}V\) from (16). By employing Eqs. (1) and (19), we can then obtain

$$\tilde{V}=V^{0}+FA\tilde{V}+(1-FA)\Delta V(g,\tilde{V}).$$
(20)

We substitute the exact expressions \(\delta^{(1)}V\) and \(\delta^{(2)}V\) (16) (which already involve \(\tilde{V}\)) into Eq. (20) and use relations (15) and (18). As a result, we obtain a new equation for \(\tilde{V}\) in the form

$$\tilde{V}=e_{q}V^{0}+FA\tilde{V}+2FGgDGgGG\tilde{V}$$
(21)
$${}+FGgGDGgG\tilde{V}+2FGg_{\tilde{1}\tilde{1}}DGG\tilde{V}$$
$${}+4FGGgG\Gamma GDgGG\tilde{V}+2FGgGGDd\Gamma GG\tilde{V}$$
$${}+2\delta FDGgGG\tilde{V}+2\delta FDGG\Gamma GgGG\tilde{V}$$
$${}+\delta FDGGd\Gamma GG\tilde{V}+\delta^{(2)}FGG\tilde{V}.$$

This equation contains 10 integral terms instead of 12 ones in Eq. (16) in [1]. (We note that, in its analytic form, we write digit 4 in the first line of Eq. (21) instead of digit 2 in its graphical representation.) Equation (21) can readily be represented in a graphic form. For our purpose of taking into account two-phonon configurations, it is better, however, to employ the amplitude \(\Gamma\) rather than the quantity \(d\Gamma\) in Eq. (21). Therefore, we transform Eq. (14) for \(d\Gamma\) into an expression for it; that is,

$$d\Gamma=\delta F+\Gamma A\delta F=\delta F+\Gamma GG\delta F.$$
(22)

Substituting Eq. (22) into Eq. (21), we obtain the following equation for \(\tilde{V}\):

$$\tilde{V}=e_{q}V^{0}+FA\tilde{V}+2FGgDGgGG\tilde{V}+FGgGDGgG\tilde{V}$$
(23)
$${}+2FGg_{\tilde{1}\tilde{1}}DGG\tilde{V}$$
$${}+4FGGgG\Gamma GDgGG\tilde{V}$$
$$+2FGGgDG\delta FGG\tilde{V}{}{}+2\delta FDGgGG\tilde{V}$$
$$+2FGGgDG\Gamma GG\delta FGG\tilde{V}{}{}+2\delta FDGG\Gamma GgGG\tilde{V}$$
$$+\delta FDGG\delta FGG\tilde{V}{}{}+\delta FDGG\Gamma GG\delta FGG\tilde{V}+\delta^{(2)}FGG\tilde{V}.$$

It includes only the quantities \(\delta F\) and \(\Gamma\). A graphic representation of this equation is shown in Fig. 5.

Equation (23) (Fig. 5) is the second main result of our article.

Fig. 5
figure 5

Graphic representation of Eq. (23).

Full size image

We have obtained a substantial generalization of Eq. (16), Fig. 6, in [1]. We now compare this with Eq. (23), Fig. 5. For the sake of simplicity, we number our formulas in accordance with their lines in Eq. (23) and Fig. 5; that is,

$$\tilde{V}=\tilde{V}^{1}+\tilde{V}^{\textrm{tad}}+\tilde{V}^{3}_{n}+\tilde{V}^{4}_{n}+\tilde{V}^{5}_{n}+\tilde{V}^{6}_{n},$$
(24)

Here, the superscript means only lines in Eq. (23), Fig. 5. The subscript \(n\) in the four terms indicates that these terms contain new parts in relation to what we had in [1].

1. We have obtained perfect agreement with the results in [1] in line 1 and in line 2 for the term \(\tilde{V}^{\textrm{tad}}\).

2. However, there are significant differences. As might have been expected, the terms that first contain the amplitude \(g\) do not appear here because of the absence of the first \(g^{2}\) correction in the form \(gGD\delta^{(1)}V\) to the vertex. But in addition to the terms containing \(F\) and \(\delta F\) (as in [1]), there appeared here five terms containing the total interaction amplitude \(\Gamma\). This makes it possible to obtain two-phonon configurations (see next section).

4.2 \(1p1h\otimes\textrm{Phonon}\) and Two-Phonon Configurations

Equation (23) makes it possible to introduce two-phonon configurations upon employing the expansion of the amplitude \(\Gamma\) in phonons; that is,

$$\Gamma(\omega)=\sum_{s}\frac{g^{s}g^{s*}}{\omega-\omega_{s}},$$
(25)

where \(g^{s}\) satisfies Eq. (4). This expansion is appropriate precisely for calculating pygmy dipole and giant multipole resonances, since an enormous number of phonons is used in them as a rule. Therefore, the expansion in Eq. (25) nearly exhausts the amplitude \(\Gamma\). In principle, one should add the regular part of the amplitude \(\Gamma\). However, this approach leads to substantial complications associated with the problem of finding the regular part of the amplitude and is not constructive at this stage. It will be considered in the near future.

Substituting expansion (25) into the quantity \(2gGD\Gamma Gg\), which plays the role of phonon-exchange interaction, we arrive at the symbolic relation

$$gDG\Gamma Gg=gGgDDgGg,$$
(26)

which is shown in Fig. 6.

Fig. 6
figure 6

Graphic representation of Eq. (26).

Full size image

In order to obtain a new equation for the vertex \(\tilde{V}\), it is necessary to substitute expression (25) into all five terms of Eq. (23), Fig. 5, that contain the amplitude \(\Gamma\). We then obtain the result shown in Fig. 7:

$$\tilde{V}=e_{q}V^{0}+FA\tilde{V}+2FGgDGgGG\tilde{V}+FGgGDGgG\tilde{V}$$
(27)
$${}+2FGg_{\tilde{1}\tilde{1}}DGG\tilde{V}$$
$$+4FGGgGgDDgGgGG\tilde{V}$$
$$+2FGGgD\delta FGG\tilde{V}{}{}+2\delta FDGgGG\tilde{V}$$
$$+2\delta FDGG\delta FGG\tilde{V}{}{}+\delta^{(2)}FDGG\tilde{V}$$
$$+\delta FGGgDDgGG\delta FGG\tilde{V}$$
$${}+2FGGgGgDDgGG\delta FGG\tilde{V}$$
$$+2\delta FGGgDDgGgGG\tilde{V}.$$
Fig. 7
figure 7

Equation (27) in the diagrammatic representation.

Full size image

The lines in Eq. (27) and Fig. 7 correspond to each other.

Figure 7 and Eq. (27) are the third main result of our present study.

5 DISCUSSION OF THE NEW EQUATION FOR THE EFFECTIVE FIELD \(\tilde{V}\)

5.1 General Description. Comparison with [1]

By employing the standard diagram technique, we can see that Eq. (27), Fig. 7, contains both \(1p1h\otimes\textrm{phonon}\) configurations in all lines, with the exception of the RPA part of Eq. (1) in line 1, and two-phonon configurations in lines 3, 6, 7, and 8 of Eq. (27). This can readily be understood by mentally making transverse cuts of the terms in Fig. 7.

Let us now number the terms in Eq. (27), Fig. 7, according to their lines; that is,

$$\tilde{V}=\tilde{V}^{1}+\tilde{V}^{\textrm{tad}}+\tilde{V}^{3}_{2\textrm{phon}}$$
(28)
$${}+\tilde{V}^{4}+\tilde{V}^{5}+\tilde{V}^{6}_{2\textrm{phon}}+\tilde{V}^{7}_{2\textrm{phon}}+\tilde{V}^{8}_{2\textrm{phon}},$$

where the superscripts 1–8 mean only the number of a line in Eq. (27), Fig. 7. The subscripts 2phon mean that the respective terms contain two-phonon configurations. Some terms in Eq. (28) include two terms.

1. We have reached perfect agreement between Eq. (16), Fig. 6, in [1] and Eq. (27), Fig. 7, in line 1 and in line 2 for the terms \(\tilde{V}^{\textrm{tad}}\).

2. Four terms in lines 4 and 5 coincide with the terms in lines 4 and 6 in Fig. 6 from [1], where they were obtained and discussed.

3. The terms in lines 6, 7, and 8—that is, \(\tilde{V}^{6}_{2\textrm{phon}}+\tilde{V}^{7}_{2\textrm{phon}}+\tilde{V}^{8}_{2\textrm{phon}}\)—contain two-phonon configurations and the quantities \((\delta F)^{2}g^{2}\) and \(\delta Fg^{3}\).

All terms in lines 4–8 contain \(\delta F\). This quantity is expressed in terms of the amplitude of the three-quasiparticle effective interaction as [13]

$$\delta_{s}F=WGg_{s}G.$$
(29)

As is well known, the role of this interaction is by and large modest. This gives grounds to believe that the quantitative contribution of these terms is small. For the problem of studying static properties, this was shown in [16] by means of a direct calculation with the aid of Eq. (7). Therefore, we will not discuss these terms here and examine below only the terms involving \(\tilde{V}^{3}_{2\textrm{phon}}\) (see next subsection). We will derive general expressions for them but, first of all, consider, in a more detailed form, new two-phonon phonon-exchange interactions stemming from the exchange of two phonons and playing the role of a new effective interaction between nucleons.

5.2 Terms \(\tilde{V}^{3}_{2\textrm{phon}}\) (line 3). Two-phonon Configurations. Comparison with the TBA Model

The two-phonon terms in line 3 have the form

$$\tilde{V}^{3}_{2\textrm{phon}}=FGGF_{\textrm{ind}\_1}^{2\textrm{phonon}}GG\tilde{V}$$
(30)
$${}+FGGF_{\textrm{ind}\_2}^{2\textrm{phonon}}GG\tilde{V}.$$

Here, we have introduced the two-phonon phonon-exchange interactions \(F^{2\textrm{phonon}}_{\textrm{ind}\_1}\) and \(F_{\textrm{ind}\_2}^{2\textrm{phonon}}\). For the first of the two-phonon graphs in Fig. 7, we have

$$(F^{2\textrm{phonon}}_{\textrm{ind}})_{1234\_1}(\varepsilon_{1},\varepsilon_{3},\omega)$$
(31)
$${}=\sum_{56ss^{\prime}}g^{s}_{15}g^{s*}_{63}g^{s^{\prime}}_{52}g^{s^{\prime}*}_{46}I_{56ss^{\prime}\_1}\delta(\varepsilon_{1}-\varepsilon_{2}+\varepsilon_{4}-\varepsilon_{3}),$$
$$I_{56ss^{\prime}\_1}(\varepsilon_{1},\varepsilon_{3})=\int G_{5}(\varepsilon_{1}-\omega_{1})$$
(32)
$${}\times G_{6}(\varepsilon_{3}-\omega_{1})D_{s}(\omega_{1})D_{s^{\prime}}(\omega_{1}-\omega)d\omega_{1},$$

where we have introduced the notation \((\varepsilon_{1}-\varepsilon_{2})=(\varepsilon_{3}-\varepsilon_{4})=\omega\). The result of integration is given by expression (35).

In the case of the second graph for \(F^{2\textrm{phonon}}_{\textrm{ind}}\), which appears in the ‘‘crossed’’ graph in line 3, Fig. 7, we have

$$(F^{2\textrm{phonon}}_{\textrm{ind}})_{1234\_2}(\varepsilon_{1},\varepsilon_{4},\omega)$$
(33)
$${}=\sum_{56ss^{\prime}}g^{s}_{15}g^{s*}_{46}g^{s^{\prime}}_{52}g^{s^{\prime}*}_{63}I_{56ss^{\prime}\_2}\delta(\varepsilon_{1}-\varepsilon_{2}+\varepsilon_{4}-\varepsilon_{3}),$$

where

$$I_{56ss^{\prime}\_2}(\varepsilon_{1},\varepsilon_{4})=\int G_{5}(\varepsilon_{1}-\omega_{1})$$
(34)
$${}\times G_{6}(\varepsilon_{4}+\omega_{1})D_{s}(\omega_{1})D_{s^{\prime}}(\omega_{1}-\omega)d\omega_{1},$$
$$I_{56ss^{\prime}\_1}=\frac{(1-n_{5})n_{6}}{(\varepsilon_{3}+\varepsilon_{5}-\varepsilon_{6}-\varepsilon_{1})(\varepsilon_{1}-\varepsilon_{5}-\omega_{s})(\varepsilon_{1}-\varepsilon_{5}-\omega-\omega_{s}^{\prime})}$$
(35)
$${}-\frac{n_{5}(1-n_{6})}{(\varepsilon_{3}+\varepsilon_{5}-\varepsilon_{6}-\varepsilon_{1})(\varepsilon_{1}-\varepsilon_{5}+\omega_{s})(\varepsilon_{1}-\varepsilon_{5}-\omega+\omega_{s}^{\prime})}$$
$${}+\frac{(1-n_{5})n_{6}}{(\varepsilon_{3}+\varepsilon_{5}-\varepsilon_{6}-\varepsilon_{1})(\varepsilon_{3}-\varepsilon_{6}+\omega_{s})(\varepsilon_{3}-\varepsilon_{6}-\omega+\omega_{s}^{\prime})}$$
$${}-\frac{n_{5}(1-n_{6})}{(\varepsilon_{3}+\varepsilon_{5}-\varepsilon_{6}-\varepsilon_{1})(\varepsilon_{3}-\varepsilon_{6}-\omega_{s})(\varepsilon_{3}-\varepsilon_{6}-\omega-\omega_{s}^{\prime})}+\frac{(1-n_{5})(1-n_{6})}{(\varepsilon_{1}-\varepsilon_{5}-\omega_{s})(\varepsilon_{3}-\varepsilon_{6}-\omega_{s})(\omega_{s}+\omega_{s}^{\prime}-\omega)}$$
$${}+\frac{n_{5}n_{6}}{(\varepsilon_{1}-\varepsilon_{5}+\omega_{s})(\varepsilon_{3}-\varepsilon_{6}+\omega_{s})(\omega_{s}+\omega_{s}^{\prime}+\omega)}+\frac{(1-n_{5})(1-n_{6})}{(\varepsilon_{1}-\varepsilon_{5}-\omega-\omega_{s}^{\prime})(\varepsilon_{3}-\varepsilon_{6}-\omega-\omega_{s}^{\prime})(\omega_{s}+\omega_{s}^{\prime}+\omega)}$$
$${}+\frac{n_{5}n_{6}}{(\varepsilon_{1}-\varepsilon_{5}-\omega+\omega_{s}^{\prime})(\varepsilon_{3}-\varepsilon_{6}-\omega+\omega_{s}^{\prime})(\omega_{s}+\omega_{s}^{\prime}-\omega)}$$
$${}+\frac{(1-n_{5})(1-n_{6})}{(\varepsilon_{3}+\varepsilon_{5}-\varepsilon_{6}-\varepsilon_{1})(\varepsilon_{1}-\varepsilon_{5}-\omega_{s})(\varepsilon_{1}-\varepsilon_{5}-\omega-\omega_{s}^{\prime})}$$
$${}-\frac{n_{5}n_{6}}{(\varepsilon_{3}+\varepsilon_{5}-\varepsilon_{6}-\varepsilon_{1})(\varepsilon_{1}-\varepsilon_{5}+\omega_{s})(\varepsilon_{1}-\varepsilon_{5}-\omega+\omega_{s}^{\prime})}$$
$${}+\frac{(1-n_{5})n_{6}}{(\varepsilon_{1}-\varepsilon_{5}-\omega_{s})(\varepsilon_{3}-\varepsilon_{6}-\omega_{s})(\omega_{s}+\omega_{s}^{\prime}-\omega)}+\frac{n_{5}(1-n_{6})}{(\varepsilon_{1}-\varepsilon_{5}+\omega_{s})(\varepsilon_{3}-\varepsilon_{6}+\omega_{s})(\omega_{s}+\omega_{s}^{\prime}+\omega)}$$
$${}+\frac{(1-n_{5})n_{6}}{(\varepsilon_{1}-\varepsilon_{5}+\omega_{s})(\varepsilon_{3}-\varepsilon_{6}+\omega_{s})(\omega_{s}+\omega_{s}^{\prime}+\omega)}+\frac{n_{5}(1-n_{6})}{(\varepsilon_{1}-\varepsilon_{5}-\omega_{s})(\varepsilon_{3}-\varepsilon_{6}-\omega_{s})(\omega_{s}+\omega_{s}^{\prime}-\omega)}.$$

The expression for \(I_{56ss^{\prime}\_2}\) is similar. We see that the two-phonon denominators \([\omega\pm(\omega_{s}+\omega^{\prime}_{s})]^{-1}\) appear both in the \(pp\) (\(n_{\lambda_{5}}n_{\lambda_{6}}\)) and \(hh\) \((1-n_{\lambda_{5}})(1-n_{\lambda_{6}})\) terms and in the \(hp\) \(((1-n_{\lambda_{5}})n_{\lambda_{6}})\) and \(ph\) \((n_{\lambda_{5}}(1-n_{\lambda_{6}}))\) terms, where \(pp\) (\(hh\)) corresponds to two particles (holes) above (below) the Fermi surface, while \(hp\) (\(ph\)) corresponds to a hole and a particle on the opposite sides of the Fermi surface.

The two-phonon terms in line 3 in Eq. (35) contain complex \(1p1h\otimes\textrm{phonon}\) and two-phonon configurations. These configurations, including those that correspond to ground-state correlations, can be seen by mentally making transverse cuts of the respective diagrams. Our two-phonon configurations also contain two-phonon ground-state correlations with the denominators \([\omega+(\omega_{s}+\omega_{s}^{\prime})]^{-1}\). Thus, the \(1p1h\otimes\textrm{phonon}\) configurations are present not only in line 1 but also in line 3 in Fig. 7; that is, we have obtained a substantially more complex structure than in [1].

Expression (35) contains both \(1p1h\otimes\textrm{phonon}\) and two-phonon configurations and is rather cumbersome. In order to simplify it and to compare the result with the TBA result [19, 32], we attempted (without success!) to reduce them by means of a computer to a form containing only terms that involve \([\omega\pm(\omega_{s}+\omega_{s}^{\prime})]^{-1}\). The result of transforming the two formulas has the form (36) and the form (37),

$$I_{56ss^{\prime}\_1}(\varepsilon_{1},\varepsilon_{3},\omega)=\frac{1}{(\varepsilon_{3}+\varepsilon_{\lambda_{5}}-\varepsilon_{\lambda_{6}}-\varepsilon_{1})}$$
(36)
$${}\times\bigg{(}\frac{1-n_{\lambda_{5}}}{(\varepsilon_{1}-\varepsilon_{\lambda_{5}}-\omega_{s})(\varepsilon_{1}-\varepsilon_{\lambda_{5}}-\omega-\omega_{s}^{\prime})}$$
$${}-\frac{n_{\lambda_{5}}}{(\varepsilon_{1}-\varepsilon_{\lambda_{5}}+\omega_{s})(\varepsilon_{1}-\varepsilon_{\lambda_{5}}-\omega+\omega_{s}^{\prime})}$$
$${}+\frac{(1-n_{\lambda_{5}})n_{6}}{(\varepsilon_{3}-\varepsilon_{\lambda_{6}}+\omega_{s})(\varepsilon_{3}-\varepsilon_{\lambda_{6}}-\omega+\omega_{s}^{\prime})}$$
$${}-\frac{n_{\lambda_{5}}(1-n_{6})}{(\varepsilon_{3}-\varepsilon_{\lambda_{6}}-\omega_{s})(\varepsilon_{3}-\varepsilon_{\lambda_{6}}-\omega-\omega_{s}^{\prime})}\bigg{)}$$
$${}+\frac{1}{(\varepsilon_{1}-\varepsilon_{\lambda_{5}}+\omega_{s})(\varepsilon_{3}-\varepsilon_{\lambda_{6}}+\omega_{s})(\omega_{s}+\omega_{s}^{\prime}+\omega)}$$
$${}+\frac{1}{(\varepsilon_{1}-\varepsilon_{\lambda_{5}}-\omega_{s})(\varepsilon_{3}-\varepsilon_{\lambda_{6}}-\omega_{s})(\omega_{s}+\omega_{s}^{\prime}-\omega)},$$
$$I_{56ss^{\prime}\_2}(\varepsilon_{1},\varepsilon_{4},\omega)=\frac{1}{(\varepsilon_{4}+\varepsilon_{1}-\varepsilon_{\lambda_{6}}-\varepsilon_{\lambda_{5}})}$$
(37)
$${}\times\bigg{(}\frac{1-n_{\lambda_{5}}}{(\varepsilon_{1}-\varepsilon_{\lambda_{5}}-\omega_{s})(\varepsilon_{1}-\varepsilon_{\lambda_{5}}-\omega-\omega_{s}^{\prime})}$$
$${}-\frac{n_{\lambda_{5}}}{(\varepsilon_{1}-\varepsilon_{\lambda_{5}}+\omega_{s})(\varepsilon_{1}-\varepsilon_{\lambda_{5}}-\omega+\omega_{s}^{\prime})}$$
$${}-\frac{(1-n_{\lambda_{5}})(1-n_{6})}{(\varepsilon_{\lambda_{6}}-\varepsilon_{4}+\omega_{s})(\varepsilon_{\lambda_{6}}-\varepsilon_{4}-\omega+\omega_{s}^{\prime})}$$
$${}+\frac{n_{\lambda_{5}}n_{6}}{(\varepsilon_{\lambda_{6}}-\varepsilon_{4}-\omega_{s})(\varepsilon_{\lambda_{6}}-\varepsilon_{4}-\omega-\omega_{s}^{\prime})}\bigg{)}$$
$${}+\frac{1}{(\varepsilon_{1}-\varepsilon_{\lambda_{5}}+\omega_{s})(\varepsilon_{4}-\varepsilon_{\lambda_{6}}-\omega_{s})(\omega_{s}+\omega_{s}^{\prime}+\omega)}$$
$${}+\frac{1}{(\varepsilon_{1}-\varepsilon_{\lambda_{5}}-\omega_{s})(\varepsilon_{4}-\varepsilon_{\lambda_{6}}+\omega_{s})(\omega_{s}+\omega_{s}^{\prime}-\omega)}.$$

Here, one can see a considerable difference from the two-phonon version in the studies based on the time-blocking approximation [19, 32]. On one hand, our method for introducing two-phonon configurations according to Fig. 7 leads to a more complicated dependence on \(\omega\) and makes it possible to include both \(1p1h\otimes\textrm{phonon}\) configurations and two-phonon configurations. On the other hand we obtained, in line 3, a complication of the graphs in line 1, and this is natural for our model. Specifically, the \(FGGgDg\) graph in line 1 is supplemented with the \(FGGF^{2\textrm{phon}}_{\textrm{ind}}\) graph—that is, the exchange of one phonon is supplemented with exchange of two phonons. However, the respective formulas in line 3, Eq. (30), become very cumbersome. Therefore, it is necessary, first of all, to consider other models of the inclusion of \(1p1h\otimes\textrm{phonon}\) and two-phonon configurations in the equation for the vertex.

6 CONCLUSIONS

The present study, which continues and develops further the analysis reported in [1], relied on nuclear quantum many-body theory—more precisely, on the method of quantum Green’s functions. We have studied a model in which one takes into account only one (the main) \(g^{2}\) correction to the vertex \(V\)—the basic important ingredient of the theory of finite Fermi systems. (This is the aspect because of which our present analysis has a model character.) As in [1], we have confirmed (that is, obtained as a particular case) the earlier model of taking into account complex configurations [17] and the TBA model [18] (the latter under the condition that one uses the TBA recipe, if necessary). At the same time, we have naturally confirmed the results obtained earlier in [1] that concern the new dynamical tadpole effect and the presence of terms containing variations of the effective interaction in the phonon field, \(\delta F\). These are two effects in which our approach differs from all previous models and methods. The new results of the present study are the following: (i) In contrast to [1], we have obtained and employed exact expressions for two variations of the vertex in the phonon field rather than approximate expressions for them. (ii) This made it possible to obtain an equation for the vertex \(\tilde{V}\) in a form that contains, in addition to the ordinary effective interaction \(F\) in the theory of finite Fermi systems, the total particle–hole interaction amplitude \(\Gamma\). (iii) By expanding this amplitude in RPA phonons, we have derived a new equation for \(\tilde{V}\) in a form that contains complex configurations—both \(1p1h\otimes\textrm{phonon}\) ones and two-phonon ones. These results are of paramount importance for a further development of a generalized theory of finite Fermi systems. However, the terms that we have obtained above with allowance for two-phonon configurations turned out to be very cumbersome for an ultimate analysis, to say nothing of the calculations. This means that the model that we have examined in the present study calls for an additional analysis, which we are going to perform in the near future.