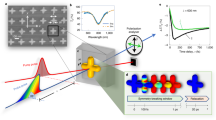
The sub- and picosecond optical response dynamics of the metal–dielectric metasurface based on gold nanospheres placed in a layer of bismuth-substituted yttrium iron garnet has been studied via the pump–probe femtosecond spectroscopy with time resolution. It is shown that the plasmon modes of the metasurface demonstrate bulk gold dynamics, while the observed relaxation of the polariton mode is slowed down by several picoseconds. The difference arise because of the detection of different processes at the wavelengths of the plasmon and polariton modes by the probe beam.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
One of the promising fields of nanophotonics is the development of technique for controlling light using metasurfaces [1, 2], that are two-dimensional subwavelength scale arrays of nanoparticles called metaatoms [3]. Metaatoms make excitation of various resonant electromagnetic modes possible, which provides enhancement of electromagnetic field energy localization inside the structure, the increase of the interaction time of light with the medium, and the control of incident light scattering. These structures have found an extensive application in biomedicine [4], sensing [5], integral [6] and topological [7] photonics, photovoltaics [8], neuromorphic [9] and analog [10] computing, nonlinear optics [11], and light control [12, 13]. The optical response of metasurfaces can be tuned by various external stimulus, for example, by electric [14] and magnetic fields [15–17], temperature [18], and laser pulses [19–22].
Noble metal nanoparticles with plasmon resonances are often used as metaatoms [17, 23–25]. The effect of ultrashort laser pulses on bulk noble metals has been widely studied by the pump–probe technique. First, the pump pulse causes the nonequilibrium dynamics of the electron gas, then the energy is redistributed, and the system comes into the equilibrium due to electron–electron, electron–phonon and phonon–phonon collisions [26–28]. These processes have typical times of hundreds of femtoseconds, few picoseconds and few nanoseconds, respectively. The induced changes in the dielectric permittivity can be observed by detecting the reflection or transmission of the probe pulse.
On the one hand, metasurfaces are sensitive to dielectric permittivity changes near a resonance, therefore they can be used to efficiently detect ultrafast processes [29]. On the other hand, an increase in interaction time of a pump beam with a medium in metasurfaces provides the stronger impact of an incident laser pulse on a structure [30]. Moreover, additional ultrafast processes may appear due to nanostructuring, for example, vibrational resonances of nanospheres with a frequency of tens of picoseconds [31]. Excitation of various electromagnetic modes by the pump beam may also cause additional ultrafast processes. Plasmon-induced transfer of electrons from gold nanoparticles to the semiconductor with subsequent relaxation were detected in metal–semiconductor metasurfaces [32]. In these structures, different dynamics of the ultrafast optical response for resonant and non-resonant pump wavelengths are observed.
Thus, several processes can occur simultaneously in metasurfaces on sub- and picosecond time scales. The optical response of multimodal systems to a medium perturbation can differ significantly depending on the excited resonance type [4]. One of the types of multimodal systems are hybrid metal–dielectric metasurfaces [16, 17, 33–35]. The presence of metallic and dielectric components in the same structure makes it possible to excite both plasmon and polariton modes. The perturbation of the medium has different effects on various modes. Therefore, the presence of processes with several timescales in hybrid metasurface leads to diverse dynamics of the optical response in the vicinity of resonances of different types.
In this paper, diverse ultrafast dynamics of the optical response are experimentally observed in a hybrid metal–dielectric Au-Bi:YIG metasurface by probing at the frequencies of polariton and plasmon modes.
The studied sample is a hybrid metal–dielectric metasurface (HMDM) [17] based on a two-dimensional periodic square array of gold nanospheres covered with a layer of bismuth-substituted yttrium iron garnet (Bi:YIG). First, periodically arranged nanodisks were obtained from a gold film on a quartz substrate by electron beam lithography. Then, the nanodisks were annealed at the temperature of 950°C for 10 min and melted to form spherical droplets. The Bi:YIG layer was sputtered on top of the nanospheres by magnetron deposition and annealed at the temperature of 750°C during 15 min for crystallization. The radius of the gold nanospheres was \({{R}_{1}} = 55\) nm, the array period in both directions was \(d = 600\) nm, Bi:YIG layer thickness was \(h = 95\) nm, the radius of Bi:YIG hemispheres over the gold particles was \({{R}_{2}} = 80\) nm. The sample supports various resonant electromagnetic excitations in the visible spectral range, in particular, the quasi-waveguide mode (QWG) and surface lattice resonances (SLR). These modes have a different nature and therefore different electromagnetic field localization. SLR arise from the coherent radiation of localized plasmons in the array, and, therefore, they are localized inside and in the vicinity of the gold nanospheres. QWG is associated with the waveguide for a diffracted beam within the Bi:YIG layer and is localized mainly in the garnet. More detailed characterization of the HMDM and the observed resonances, as well as the pattern of the sample, can be found in [16, 17].
Time-resolved pump–probe femtosecond spectroscopy was used to study ultrafast processes in the metasurface. The radiation source was a Ti:sapphire laser with a regenerative amplifier of 70-fs pulse duration, 800-nm central wavelength and 1-kHz repetition rate. The normally incident pump beam was linearly polarized along one of the periodicity axis. It excited dipole SLR, which led to resonant radiation absorption in the HMDM [17]. The fluence of the pump beam J was varied from 0 to 1.2 mJ/cm2.
To perform spectroscopy, a supercontinuum was generated by the probe beam in the spectral range from 450 to 1400 nm using a sapphire plate. Wavelengths greater than 750 nm were cut off by a shortpass filter. The wide spectral range of the supercontinuum allowed the probe beam to detect several electromagnetic modes of a multiresonant metasurface at once for each delay time between pump and probe pulses. The angle of incidence of the p-polarized probe beam was 17°.
Experimental observation of the optical response dynamics was carried out by measuring the differential transmittance:
where \(T(\lambda ,\tau )\) is the transmittance of the sample under the pump beam influence, \(T(\lambda )\) is the unperturbed transmittance, τ is the time delay between pump and probe pulses.
The differential transmittance spectra of the HMDM were measured in a wide spectral range for various delay times and fluences of the pump beam. Figure 1 shows a two-dimensional evolution map of the \(\Delta T{\text{/}}T\) spectra. Figure 2 shows its cross sections at different delay times and wavelengths for the fluence of \(J = 0.6\) J/cm2.
(Color online) (a) Cross sections of differential transmittance \(\Delta T{\text{/}}T(\lambda )\) for different delay times. (b) \(\Delta T{\text{/}}T(\tau )\) cross sections for different wavelengths normalized on maximum, the wavelengths are marked with arrows in the panel (a); the inset shows the cross section at 523 nm near zero value of \(\Delta T{\text{/}}T\).
A femtosecond laser pump pulse is resonantly absorbed by gold nanospheres, which leads to temperature increase of the electron gas and the associated change in the dielectric permittivity of gold [36, 37]. Therefore, the high sensitivity of the HMDM electromagnetic modes to the excitation within the probe spectral range leads to the resonant enhancement of the \(\Delta T{\text{/}}T\) value. Several noteworthy features are observed in the \(\Delta T{\text{/}}T\) spectra. There are two peaks in the vicinity of 540 nm, two peaks in the vicinity of 630 nm and the peak at 730 nm. As it was shown earlier [16, 17], these peaks are spectrally close to the excitation wavelengths of the QWG, the quadrupole SLR and the dipole SLR, respectively. The dip in the short-wavelength part of the spectrum occurs due to a growth of the gold absorption associated with the increase in the d-transition probability at high temperatures of the electron gas [36, 37].
Figure 2b shows the time cross sections of the differential transmittance normalized to the maximum value for several wavelengths. \(\Delta T{\text{/}}T\) dynamics in the vicinity of the dipole SLR at the wavelength of 730 nm is typical for the ultrafast optical response of gold at this wavelength [26, 28, 38]. An absorbed pump pulse excites free electron gas to the highly non-equilibrium state, which is not described by the Fermi distribution. During the thermalization time \({{\tau }_{{ee}}}\) the electron gas relaxes into a Fermi state with elevated temperature by electron–electron collisions. The thermalization process is a rise at the \(\Delta T{\text{/}}T\) time dependence, while its completion corresponds to an extremum. In addition to collisions with each other, hot electrons also can collide with lattice and transfer energy to phonons. Since the probability of the scattering is significantly less than that of electron–electron process, the electron–phonon relaxation time \({{\tau }_{{ep}}}\) greatly exceeds \({{\tau }_{{ee}}}\). The thermalization of electrons is described by the kinetic Boltzmann equation [39] at short time, and by two-temperature model later [40].
The electron–phonon relaxation in Fig. 2b corresponds to the exponential decay after reaching the extremum. The thermalization time \({{\tau }_{{ee}}} = 160\) fs and electron–phonon relaxation time \({{\tau }_{{ep}}} = 2.4\) ps were obtained using the experimental data fitting, the method is described in details in [29]. The values correspond to the data reported in the literature [38]. The gold’s phonon subsystem, having reached equilibrium with the electron one, begins to give off the heat to the garnet. This happens at the hundreds of picoseconds timescale and is beyond the scope of consideration. \(\Delta T{\text{/}}T\) dependences on time in the vicinity of the quadrupole SLR and at the short-wavelength dip also correspond to the typical optical response dynamics of gold (Fig. 2b). Consequently, the dynamics of the optical response in the sub- and picosecond time scale is mainly determined by the processes in gold in a wide spectral region. The differences at the large delays are related to the different spectral dependence of the electron and phonon temperatures contributions to the dielectric permittivity.
However, the dynamics of differential transmittance in the vicinity of the QWG shows significant dissimilarity (Fig. 3a). \(\Delta T{\text{/}}T\) reaches its extremum at longer delay time \({{\tau }_{1}}\), and then maintains the extremum values during \({{\tau }_{{\text{2}}}}\) of the order of several hundred femtoseconds, in contrast to other spectral regions. After that a relaxation is observed with a typical time of \({{\tau }_{3}} > {{\tau }_{{ep}}}\). Thus, there is a slowdown in the ultrafast optical response at the QWG wavelengths.
(Color online) (a) \(\Delta T{\text{/}}T(\tau )\) cross sections for several wavelengths near the QWG normalized on the maximum value; the inset: \(\Delta T{\text{/}}T(\lambda )\) spectrum near the QWG and arrows indicating considered wavelengths. (b) Normalized \(\Delta T{\text{/}}T(\tau )\) cross sections at 527 nm wavelength for several fluences; the inset shows normalized \(\Delta T{\text{/}}T(\tau )\) cross sections at 730 nm wavelength for the same fluences.
Moreover, the behavior of differential transmittance near the quasi-waveguide mode varies depending on the considered spectral position: the times \({{\tau }_{1}}\), \({{\tau }_{2}}\), \({{\tau }_{3}}\) increase while moving from the maximum of differential transmittance at the wavelength of 530 nm to the short-wavelength region (Fig. 3a). At the wavelengths where \(\Delta T{\text{/}}T\) values are close to 0, differential transmittance evolution takes a qualitatively different shape: there is negative extremum at first, then \(\Delta T{\text{/}}T\) passes through 0 to the positive values during subpicosecond time (Fig. 2b, inset). However, the low signal-to-noise ratio does not allow us to obtain reliable times. In the spectral region where \(\Delta T{\text{/}}T < 0\), the dynamics is also described by the processes typical for gold.
The shape of \(\Delta T{\text{/}}T(\tau )\) dependence for other pump fluences is qualitatively preserved, but the times change (Fig. 3b). In the spectral vicinity of plasmon resonances and in the region of the interband transition, \(\Delta T{\text{/}}T\) relaxation slows down with an increase of J (Fig. 3b, inset). This change is related to the electron–phonon relaxation time dependence on the temperature of the lattice [27, 41]. In the spectral vicinity of the QWG existence the differential transmittance dynamics lag became more pronounced with an increase of J. An increase of \({{\tau }_{1}}\), \({{\tau }_{2}}\) and \({{\tau }_{3}}\) was observed.
The \(\Delta T{\text{/}}T(J)\) dependences at fixed delay times were also measured (Fig. 4). In the vicinity of the dipole plasmon resonance the expected [26, 38] linear dependence on the fluence was observed for all the studied delay times. Linear dependence was also observed in the remaining spectral regions, with the exception of the QWG resonance. In its vicinity \(\Delta T{\text{/}}T\) rises with an increase of J sublinearly. The divergence from linear dependence was more pronounced at short delay times (Fig. 4b). Similar to \(\Delta T{\text{/}}T(\tau )\) dependence, \(\Delta T{\text{/}}T(J)\) varies in the spectral vicinity of the QWG at the blue slope of the resonance (Fig. 4a): \(\Delta T{\text{/}}T(J)\) dependence diverges stronger for shorter wavelengths. If differential transmittance is close to zero, the dependence on fluence shows an extremum and changes the sign of \(\Delta T{\text{/}}T\). As \(\Delta T{\text{/}}T < 0\), the dependence becomes linear. To compare the different wavelengths, \(\Delta T{\text{/}}T(J)\) normalization was performed in Fig. 4 in a way that linear parts of \(\Delta T{\text{/}}{{T}_{{{\text{norm}}}}}\) at low fluences coincides for all wavelengths.
In conclusions, an anomalous picosecond optical transmittance dynamics of the Au-Bi:YIG hybrid metasurface was experimentally detected in the narrow spectral window corresponding to the excitation of a quasi-waveguide mode by a probe beam. The studied multimodal metasurface possesses modes that are different in nature and localization configurations. Plasmon modes are localized in the vicinity of nanospheres, therefore the dielectric permittivity change of gold contributes dominantly to the \(\Delta T{\text{/}}T\) evolution. Since the dip in the differential transmittance spectrum is associated with an interband transition in gold, \(\Delta T{\text{/}}T\) dynamics at the wavelength is also determined by the dielectric permittivity evolution of gold. In turn, the quasi-waveguide mode is localized in the garnet layer, thus a change in the garnet state will have a stronger effect on it than on the other features in the spectrum. Probing at the wavelengths near quasi-waveguide modes makes it possible to detect a process that did not appear at other resonances: differential transmittance demonstrates dependencies of \(\Delta T{\text{/}}T(\tau )\) and \(\Delta T{\text{/}}T(J)\) qualitatively different from the curves obtained for the rest of the spectral range. In addition to changing a state of the garnet layer, another possible mechanism of the observed differences in dynamics is a change in the configuration of the waveguide due to the thermal expansion of the gold nanospheres.
REFERENCES
A. I. Kuznetsov, A. E. Miroshnichenko, M. L. Brongersma, Y. S. Kivshar, and B. S. Luk’yanchuk, Science (Washington, DC, U. S.) 354, aag2472 (2016).
M. R. Shcherbakov, S. Liu, V. V. Zubyuk, A. Vaskin, P. P. Vabishchevich, G. Keeler, T. Pertsch, T. V. Dolgova, I. Staude, I. Brener, and A. A. Fedyanin, Nat. Commun. 8, 17 (2017).
N. Meinzer, W. L. Barnes, and I. R. Hooper, Nat. Photon. 8, 889 (2014).
D. Rodrigo, A. Tittl, N. Ait-Bouziad, A. John-Herpin, O. Limaj, C. Kelly, D. Yoo, N. J. Wittenberg, S.‑H. Oh, H. A. Lashuel, and H. Altug, Nat. Commun. 9, 2160 (2018).
D. Ray, T. V. Raziman, C. Santschi, D. Etezadi, H. Altug, and O. J. F. Martin, Nano Lett. 20, 8752 (2020).
Z. Wang, Y. Xiao, K. Liao, T. Li, H. Song, H. Chen, S. M. Z. Uddin, D. Mao, F. Wang, Z. Zhou, B. Yuan, W. Jiang, N. K. Fontaine, A. Agrawal, A. E. Willner, and X. Hu, Nanophotonics 11, 3531 (2022).
A. S. Ustinov, A. S. Shorokhov, and D. A. Smirnova, JETP Lett. 114, 719 (2021).
S. Makarov, A. Furasova, E. Tiguntseva, A. Hemmetter, A. Berestennikov, A. Pushkarev, A. Zakhidov, and Y. Kivshar, Adv. Opt. Mater. 7, 1800784 (2019).
C. Wu, H. Yu, S. Lee, R. Peng, I. Takeuchi, and M. Li, Nat. Commun. 12, 1 (2021).
X. Zhang, Y. Zhou, H. Zheng, A. E. Linares, F. C. Ugwu, D. Li, H.-B. Sun, B. Bai, and J. G. Valentine, Nano Lett. 21, 8715 (2021).
K. I. Okhlopkov, A. Zilli, A. Tognazzi, D. Rocco, L. Fagiani, E. Mafakheri, M. Bollani, M. Finazzi, M. Celebrano, M. R. Shcherbakov, C. D. Angelis, and A. A. Fedyanin, Nano Lett. 21, 10438 (2021).
F. Qin, L. Ding, L. Zhang, F. Monticone, C. C. Chum, J. Deng, S. Mei, Y. Li, J. Teng, M. Hong, S. Zhang, A. Alu, and C.-W. Qiu, Sci. Adv. 2, e1501168 (2016).
A. D. Gartman, A. S. Ustinov, A. S. Shorokhov, and A. A. Fedyanin, JETP Lett. 114, 441 (2021).
S. Lepeshov and A. Krasnok, Nat. Nanotechnol. 16, 615 (2021).
D. O. Ignatyeva, D. M. Krichevsky, V. I. Belotelov, F. Royer, S. Dash, and M. Levy, J. Appl. Phys. 132, 100902 (2022).
A. V. Chetvertukhin, A. I. Musorin, T. V. Dolgova, H. Uchida, M. Inoue, and A. A. Fedyanin, J. Magn. Magn. Mater. 383, 110 (2015).
A. I. Musorin, A. V. Chetvertukhin, T. V. Dolgova, H. Uchida, M. Inoue, B. S. Luk’yanchuk, and A. A. Fedyanin, Appl. Phys. Lett. 115, 151102 (2019).
S. Abdollahramezani, O. Hemmatyar, M. Taghinejad, H. Taghinejad, Y. Kiarashinejad, M. Zandehshahvar, T. Fan, S. Deshmukh, A. A. Eftekhar, W. Cai, E. Pop, M. A. El-Sayed, and A. Adibi, Nano Lett. 21, 1238 (2021).
V. Zubyuk, L. Carletti, M. Shcherbakov, and S. Kruk, APL Mater. 9, 060701 (2021).
P. A. Shafirin, V. V. Zubyuk, A. A. Fedyanin, and M. R. Shcherbakov, Nanophotonics 11, 4053 (2022).
A. Basiri, Md Z. E. Rafique, J. Bai, S. Choi, and Y. Yao, Light Sci. Appl. 11, 102 (2022).
Y. Wu, L. Kang, H. Bao, and D. H. Werner, ACS Photon. 7, 2362 (2020).
M. Mayer, M. J. Schnepf, T. A. F. König, and A. Fery, Adv. Opt. Mater. 7, 1800564 (2019).
J. Wang, A. Coillet, O. Demichel, Z. Wang, D. Rego, A. Bouhelier, P. Grelu, and B. Cluzel, Light Sci. Appl. 9, 50 (2020).
V. G. Kravets, A. V. Kabashin, W. L. Barnes, and A. N. Grigorenko, Chem. Rev. 118, 5912 (2018).
C.-K. Sun, F. Vallée, L. H. Acioli, E. P. Ippen, and J. G. Fujimoto, Phys. Rev. B 50, 15337 (1994).
R. Groeneveld, R. Sprik, and A. D. Lagendijk, Phys. Rev. B 51, 11433 (1995).
N. Del Fatti, R. Bouffanais, F. Vallée, and C. Flytzanis, Phys. Rev. Lett. 81, 922 (1998).
I. A. Novikov, M. A. Kiryanov, P. K. Nurgalieva, A. Yu. Frolov, V. V. Popov, T. V. Dolgova, and A. A. Fedyanin, Nano Lett. 20, 8615 (2020).
V. V. Zubyuk, P. P. Vabishchevich, M. R. Shcherbakov, A. S. Shorokhov, A. N. Fedotova, S. Liu, G. Keeler, T. V. Dolgova, I. Staude, I. Brener, and A. A. Fedyanin, ACS Photon. 6, 2797 (2019).
G. V. Hartland, Chem. Rev. 111, 3858 (2011).
H. Harutyunyan, A. B. F. Martinson, D. Rosenmann, L. K. Khorashad, L. V. Besteiro, A. O. Govorov, and G. P. Wiederrecht, Nat. Nanotechnol. 10, 770 (2015).
J. Guan, J. E. Park, S. Deng, M. J. H. Tan, J. Hu, and T. W. Odom, Chem. Rev. 122, 15177 (2022).
Á. Barreda, F. Vitale, A. E. Minovich, C. Ronning, and I. Staude, Adv. Photon. Res. 3, 2100286 (2022).
M. G. Barsukova, A. I. Musorin, A. S. Shorokhov, and A. A. Fedyanin, APL Photon. 4, 016102 (2019).
R. Rosei, F. Antonangeli, and U. M. Grassano, Surf. Sci. 37, 689 (1973).
M. Guerrisi, R. Rosei, and P. Winsemius, Phys. Rev. B 12, 557 (1975).
T. Stoll, P. Maioli, A. Crut, and F. Vallée, Eur. Phys. J. B 87, 1 (2014).
N. Del Fatti, C. Voisin, M. Achermann, S. Tzortzakis, D. Christofilos, and F. Vallée, Phys. Rev. B 61, 16956 (2000).
S. I. Anisimov, B. L. Kapeliovich, and T. L. Perel’man, Sov. Phys. JETP 39, 375 (1974).
S.-S. Wellershoff, J. Hohlfeld, J. Güdde, and E. Matthias, Appl. Phys. A 69, S99 (1999).
Funding
This work was supported by the Russian Science Foundation (project no. 22-22-00856). The samples characterization equipment was provided under the Moscow State University development program.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
The authors declare that they have no conflicts of interest.
Rights and permissions
Open Access. This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kiryanov, M.A., Ostanin, G.S., Dolgova, T.V. et al. Anomalous Picosecond Optical Transmittance Dynamics in Au-Bi:YIG Hybrid Metasurface. Jetp Lett. 117, 196–201 (2023). https://doi.org/10.1134/S0021364022603220
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0021364022603220