Quasi-one-dimensional (1D) linear-chain ternary iron chalcogenides AFeX2 (A = K, Rb; X = S, Se) have recently begun to attract some attention due to their wide range of possible applications. Recent studies have shown that the antiferromagnetic state can be effectively controlled using the Neel Spin–Orbit Torque (NSOT) field [1–4]. It is shown that the limiting factor for the rate of state change and, consequently, the operating frequency is the magnon velocity in the antiferromagnetic crystal [5]. This new discovery suggests that AFeS2 are promising compounds for this purpose due to their high magnon velocities; i.e., KFeS2 has a magnon velocity of 90 km/s with fr-equencies up to 10 THz [6], while other known antiferromagnetic systems have values in the range of 10‒40 km/s. Other work suggests that doped iron chalcogenides AFeX2 are possible candidates for high temperature superconductivity [7].

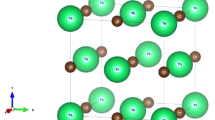
The AFeX2 (A = K, Rb; X = S, Se) compounds crystallize into monoclinic structure Fig. 1 with C2/c space group [8]. The main motif of the crystal structure is a chain of [FeX4] tetrahedral sharing a common edge and aligned along the crystallographic axis c [8]. These chains are cross-linked by alkali atoms to form a three-dimensional structure. The chains are characterized by the short Fe–Fe distance (2.815 Å) [8] not much exceeding the Fe–Fe distance of metallic iron (2.48 Å). Previous neutron diffraction experiments on powdered samples [8] have shown that KFeSe2 is a three-dimensional antiferromagnetic compound with \({{T}_{{\text{N}}}} = 310\) K and magnetic moment on Fe ions of 3 \({{\mu }_{{\text{B}}}}\).

Fig. 1.
figure 1

(Color online) Crystal structure of KFeSe2. The FeSe4 tetrahedra, with Fe drawn as the orange sphere in the center and Se as the green sphere at the corners, are highlighted in transparent green color. Large violet spheres denote K ions.

Full size image

As shown in our previous work [9], in order to correctly describe a KFeS2 crystal in terms of the density functional theory, it is necessary to use the DFT + U approximation. Strongly non-localized states of Fe 3d electrons cannot be satisfactorily described by the Generalized Gradient Approximation (GGA), and it is necessary to introduce a Hubbard-like correction to take these electrons into account explicitly. In [10] for KFeS2 we used the rotationally invariant LSDA + U approach [11] with parameters \(U = 1.5{\kern 1pt} \) eV and \(J = \) 2 eV, where U is the on-site Coulomb repulsion and J is the exchange interaction. The parameter values had been approbated on the electronic structure, magnetic subsystem, and phonon spectrum of the KFeS2 crystal. Due to the lack of experimental data necessary for selecting the parameters U and J for KFeSe2, we will use standard DFT as the first approach to the vibrational properties of KFeSe2. Calculations were performed in VASP [12–15] a part of MedeA software package. The GGA-PBEsol was used as the functional for the exchange-correlation energy [16]. The CUTOFF-energy for the plane wave basis set was selected to be equal to 500 eV. Integration over the Brillouin zone was performed on a Monkhorst–Pack 7 × 3 × 5 grid, which corresponds to actual spacing of 0.178 × 0.182 × 0.191 Å–1. An equilibrium geometry has been obtained after several stages of full structure relaxation, which includes optimization of atomic positions, cell shape, and cell volume. The fully optimized equilibrium structure was used for calculation of the phonon density of states. The phonon density of states was obtained making use of MedeA PHONON module, which implements a direct approach of harmonic approximation [17]. The calculations were carried out in the antiferromagnetic state of the crystal.

The phonon densities of states, total and element specific, were calculated as described above and are presented in Fig. 2. Each vibrational mode is simultaneously Raman and infrared active and belongs to one of the two irreducible representations of the C2 point-group symmetry corresponding to the structure of KFeSe2. The phonon density of states could be divided into two distinct areas: the low and high-frequency areas. The low-frequency area extends up to 4 THz, it shows Debye-like frequency dependence (approximately up to 3 THz), and the dominant contribution to this area comes from K and Se atoms. The high-frequency area shows a significant amount of phonon density of states and consists of only vibrational modes of Fe and Se atoms. Because of the large number of high-frequency vibrational modes, the Debye model cannot be applied for a fine analysis of the vibrational properties of the system, such as the lattice specific heat or mean-square displacement of atoms.

Fig. 2.
figure 2

(Color online) Calculated phonon density of states in KFeSe2: element-specific (K, Fe and Se atoms from the bottom towards the top) and the total PDOS (the bottom).

Full size image

The phonon density of states enables to calculate lattice contribution to the specific heat directly by using the quasi-harmonic approximation. The lattice heat capacity is determined as follows:

$$\begin{gathered} C(T) \\ = D{{k}_{{\text{B}}}}\int\limits_0^\infty g(\omega ){{\left( {\frac{{\hbar \omega }}{{2{{k}_{{\text{B}}}}T}}} \right)}^{2}}\frac{{\exp (\hbar \omega {\text{/}}{{k}_{{\text{B}}}}T)}}{{{{{\left[ {\exp (\hbar \omega {\text{/}}{{k}_{{\text{B}}}}T) - 1} \right]}}^{2}}}}d\omega , \\ \end{gathered} $$

where D is the number of degrees of freedom in the unit cell; \(g(\omega \)) is the total phonon density of states (Fig. 2, bottom), \(\hbar \) and \({{k}_{{\text{B}}}}\) are the reduced Planck and Boltzmann constants, respectively; and T is the temperature.

The calculated lattice contribution to the specific heat is presented in Fig. 3. The lattice heat capacity reaches a value of 96 J K–1 mol–1 at a temperature of 300 K and does not exceed Dulong–Petit law’s limit (about 99 J K–1 mol–1).

Fig. 3.
figure 3

(Color online) Temperature dependence of the lattice specific heat of KFeSe2.

Full size image

To summarize, phonon density of states has been calculated utilizing DFT and direct approach of harmonic approximation. Lattice contribution to the heat capacity was calculated using PDOS. The lattice specific heat could be used in a future detailed analysis of magnetic properties of KFeSe2 such as magnetic specific heat and entropy of magnetic subsystem. Is should be noted that the system under consideration potentially cannot be correctly described in terms of standard non-U DFT approach, and it is necessary to introduce Hubbard-like corrections to system energy functional. So, in the case of magnetically ordered compounds right choice of the Hubbard parameter is necessary for the correct description of magnetic ground state and magnetic moment value [9].