Angular Dependence of the Polarization Transfer to the Proton in the $e\vec {p} \to e\vec {p}$ Process

The dependence of the longitudinal polarization transfer to the proton in the $e\vec {p} \to e\vec {p}$ process on the proton scattering angle has been numerically analyzed for the case where the initial (at rest) proton is partially polarized along the direction of motion of the detected recoil proton. The analysis is based on the results of JLab polarization experiments on measuring the ratio of the Sachs form factors in the $\vec {e}p \to e\vec {p}$ process using the Kelly (2004) and Qattan (2015) parameterizations for their ratio, in the kinematics of the SANE Collaboration experiment (2020) on measuring the double spin asymmetry in the $\vec {e}\vec {p} \to ep$ process. It is shown that the violation of the scaling of the Sachs form factors leads to a significant increase in the magnitude of the polarization transfer to the proton in comparison with the case of dipole dependence.

INTRODUCTION

The proton electric (${{G}_{E}}$) and magnetic (${{G}_{M}}$) form factors, the so-called Sachs form factors (SFFs), have been experimentally studied since the 1950s in the elastic scattering of unpolarized electrons by a proton. All experimental data on the behavior of the SFFs have been obtained using the Rosenbluth technique based on the application of the Rosenbluth cross section (within the one-photon exchange approximation) for the $ep \to ep$ process in the rest frame of the initial proton [1]:

$$\frac{{d\sigma }}{{d{{\Omega }_{e}}}} = \frac{{{{\alpha }^{2}}{{E}_{2}}\mathop {\cos }\nolimits^2 ({{\theta }_{e}}{\text{/}}2)}}{{4E_{1}^{3}\mathop {\sin }\nolimits^4 ({{\theta }_{e}}{\text{/}}2)}}\frac{1}{{1 + {{\tau }_{p}}}}\left( {G_{E}^{2} + \frac{{{{\tau }_{p}}}}{\varepsilon }G_{M}^{2}} \right).$$

(1)

Here, ${{\tau }_{p}} = {{Q}^{2}}{\text{/}}4{{M}^{2}}$, ${{Q}^{2}} = 4{{E}_{1}}{{E}_{2}}\mathop {\sin }\nolimits^2 ({{\theta }_{e}}{\text{/}}2)$ is the squared 4-momentum transfer to the proton; M is the proton mass; ${{E}_{1}}$ and ${{E}_{2}}$ are the energies of the initial and final electrons, respectively; ${{\theta }_{e}}$ is the electron scattering angle; ε is the degree of linear (transverse) polarization of the virtual photon [2–5]; and $\alpha = 1{\text{/}}137$ is the fine-structure constant.

As follows from Eq. (1), the main contribution to the cross section for the $ep \to ep$ process at large ${{Q}^{2}}$ values is from the term proportional to $G_{M}^{{{\kern 1pt} 2}}$; hence, the extraction of the contribution of $G_{E}^{{{\kern 1pt} 2}}$ even at ${{Q}^{2}}\; \geqslant$ 2 GeV² is a challenging problem [6, 7].

Using the Rosenbluth technique, the dipole dependence of the SFF on Q² in the range ${{Q}^{2}}\;\leqslant \;6$ GeV² was established [6, 7]. The ${{G}_{E}}$ and ${{G}_{M}}$ values turned out to be connected by the scaling relation ${{G}_{M}} \approx {{\mu }_{p}}{{G}_{E}}$, as a result of which the following approximate equality is valid for the ratio $R \equiv {{\mu }_{p}}{{G}_{E}}{\text{/}}{{G}_{M}}$ (${{\mu }_{p}} = 2.79$ is the proton magnetic moment):

$$R \approx {\text{ }}1.$$

(2)

Akhiezer and Rekalo [3] proposed a method for measuring the R ratio based on the phenomenon of polarization transfer from the initial electron to the final proton in the $\vec {e}p \to e\vec {p}$ process. The precision experiments based on this method, performed at the Thomas Jefferson National Accelerator Facility (JLab, United States) [8–10], revealed that the R ratio decreases rapidly with an increase in ${{Q}^{2}}$, which indicates violation of the SFF dipole dependence (scaling). This decrease turned out to be linear in the range 0.4 GeV² ⩽ ${{Q}^{2}}$ ⩽ 5.6 GeV².

Measurements of the R ratio, repeated with a higher accuracy [11–15] in a wide range of ${{Q}^{2}}$ values up to 8.5 GeV², using both the Akhiezer–Rekalo method [3] and the Rosenbluth technique [15], only confirmed the discrepancy of the results.

Experimental values of R were obtained by the SANE collaboration [16] using the third approach [17]: they were extracted from the measurements of the double spin asymmetry in the $\vec {e}\vec {p} \to ep$ process in the case of partial polarization of the electron beam and proton target. The degree of polarization of the proton target (${{P}_{t}}$) was ${{P}_{t}} = (70 \pm 5)$%. The experiment was performed at two electron beam energies ${{E}_{1}}$, 5.895 and 4.725 GeV, and two ${{Q}^{2}}$ values, 2.06 and 5.66 GeV². The R values extracted in [16] are in agreement with the results of the previous polarization experiments carried out at the JLab [8–14].

The fourth method for measuring the R ratio was proposed in [18–22]; it is based on the polarization transfer from the initial to the final proton in the elastic process

$$e({{p}_{1}}) + \vec {p}{\kern 1pt} ({{q}_{1}},{{s}_{1}}) \to e({{p}_{2}}) + \vec {p}{\kern 1pt} ({{q}_{2}},{{s}_{2}})$$

(3)

in the case where initial (at rest) and final protons are fully or partially polarized and have a common spin quantization axis, coinciding with the direction of motion of the detected recoil proton. This method can also be applied in the two-photon exchange approximation; it allows one to measure the squared moduli of generalized SFFs [20]. This line of research was started in [18].

Note that Akhiezer and Rekalo (see [4], pp. 211–215) performed also general calculation of the $e\vec {p} \to e\vec {p}$ cross section in the Breit system for the case of partially polarized initial and final protons. However, they analyzed this cross section in [4] by analogy with [3] and overlooked a more interesting case, which is considered here and was discussed in [18–22].

Based on the results of JLab’s polarization experiments, aimed at measuring the R ratio in the $\vec {e}p \to e\vec {p}$ process, a numerical analysis of the ${{Q}^{2}}$ dependence of the ratio of the cross sections without and with proton spin flip, the polarization asymmetry in the $e\vec {p} \to e\vec {p}$ process, and the longitudinal polarization transfer to the proton in the kinematics of the experiment [16] in the case where the initial (at rest) and final protons are polarized and have a common spin quantization axis, coinciding with the direction of motion of the detected final recoil proton, was performed in [21, 22]. It was shown that the polarization transfer to the proton is fairly sensitive to the form of the dependence of the SFF ratio R on ${{Q}^{2}}$, i.e., to the choice of the parameterization for the R ratio.

In this study, based on the results of JLab’s polarization experiments on measuring the SFF ratio in the $\vec {e}p \to e\vec {p}$ process, using the Kelly [23] (2004) and Qattan [24] (2015) parameterizations for their ratio, in the kinematics of SANE’s experiment [16] on measuring the double spin asymmetry in the $\vec {e}\vec {p} \to ep$ process, a numerical analysis of the dependence of the longitudinal polarization transfer to the proton in the $e\vec {p} \to e\vec {p}$ process on the proton scattering angle is performed for the case where the initial (at rest) proton is partially polarized along the direction of motion of the detected recoil proton.

CROSS SECTION FOR THE $e\vec {p} \to e\vec {p}$ PROCESS IN THE REST FRAME OF THE INITIAL PROTON

Let us consider the spin 4-vectors ${{s}_{1}}$ and ${{s}_{2}}$ of the initial and final protons with 4-momenta ${{q}_{1}}$ and ${{q}_{2}}$ in process (3) in an arbitrary reference frame. The conditions of orthogonality (${{s}_{i}}{{q}_{i}} = 0$) and normalization ($s_{i}^{2} = - 1$) make it possible to determine unambiguously the expressions for their time and space components ${{s}_{i}} = ({{s}_{{i0}}},{{{\mathbf{s}}}_{i}})$ in terms of their 4-velocities ${{v}_{i}} = {{q}_{i}}{\text{/}}M$ ($i = 1,2$):

$${{s}_{i}} = ({{s}_{{i0}}},{{{\mathbf{s}}}_{i}}),\quad {{s}_{{i0}}} = {{{\mathbf{v}}}_{i}}{\kern 1pt} {{{\mathbf{c}}}_{i}},\quad {{{\mathbf{s}}}_{i}} = {{{\mathbf{c}}}_{i}} + \frac{{({{{\mathbf{c}}}_{i}}{{{\mathbf{v}}}_{i}}){\kern 1pt} {{{\mathbf{v}}}_{i}}}}{{1 + {{v}_{{i0}}}}},$$

(4)

where the unit 3-vectors ${{{\mathbf{c}}}_{i}}$ (${\mathbf{c}}_{i}^{2} = 1$) are spin quantization axes.

In the laboratory reference frame, where ${{q}_{1}} = (M,{\mathbf{0}})$ and ${{q}_{2}} = ({{q}_{{20}}},{{{\mathbf{q}}}_{2}})$, the spin quantization axes ${{{\mathbf{c}}}_{1}}$ and ${{{\mathbf{c}}}_{2}}$ are chosen so as to coincide with the direction of motion of the final proton:

$${\mathbf{c}} = {{{\mathbf{c}}}_{1}} = {{{\mathbf{c}}}_{2}} = {{{\mathbf{n}}}_{2}} = {{{\mathbf{q}}}_{2}}{\text{/|}}{{{\mathbf{q}}}_{2}}{\text{|}}.$$

(5)

Then the spin 4-vectors of the initial (${{s}_{1}}$) and final (${{s}_{2}}$) protons take the form

$${{s}_{1}} = (0,{{{\mathbf{n}}}_{2}}),\quad {{s}_{2}} = ({\text{|}}{{{\mathbf{v}}}_{2}}{\text{|}},{{v}_{{20}}}{\kern 1pt} {{{\mathbf{n}}}_{2}}),\quad {{{\mathbf{n}}}_{2}} = {{{\mathbf{q}}}_{2}}{\text{/|}}{{{\mathbf{q}}}_{2}}{\text{|}}.$$

(6)

The method proposed in [18–22] is based on the expression for the differential cross section for pro-cess (3) in the laboratory reference frame for the case where the initial and final protons are polarized and have a common spin quantization axis ${\mathbf{c}}$ (5):

$$\frac{{d{{\sigma }_{{{{\delta }_{1}},{{\delta }_{2}}}}}}}{{d{{\Omega }_{e}}}} = {{\omega }_{ + }}{{\sigma }^{{ \uparrow \uparrow }}} + {{\omega }_{ - }}{{\sigma }^{{ \downarrow \uparrow }}},$$

(7)

$${{\sigma }^{{ \uparrow \uparrow }}} = {{\sigma }_{M}}{\kern 1pt} G_{E}^{2},\quad {{\sigma }^{{ \downarrow \uparrow }}} = {{\sigma }_{M}}\frac{{{{\tau }_{p}}}}{\varepsilon }{\kern 1pt} G_{M}^{2},$$

(8)

$${{\sigma }_{M}} = \frac{{{{\alpha }^{2}}{{E}_{2}}\mathop {\cos }\nolimits^2 ({{\theta }_{e}}{\text{/}}2)}}{{4E_{1}^{{{\kern 1pt} 3}}\mathop {\sin }\nolimits^4 ({{\theta }_{e}}{\text{/}}2)}}\frac{1}{{1 + {{\tau }_{p}}}}.$$

(9)

Here, ${{\omega }_{ \pm }}$ are polarization factors:

$${{\omega }_{ + }} = (1 + {{\delta }_{1}}{{\delta }_{2}}){\text{/}}2,\quad {{\omega }_{ - }} = (1 - {{\delta }_{1}}{{\delta }_{2}}){\text{/}}2,$$

(10)

where ${{\delta }_{{1,2}}}$ are the doubled projections of the spins of the initial and final protons on the spin quantization axis c (5). Note that Eq. (7) is valid at $- 1\;\leqslant \;{{\delta }_{{1,2}}}\;\leqslant \;1$.

Formula (7), as well as (1), is the sum of two terms, one of which contains only $G_{E}^{{{\kern 1pt} 2}}$, while the other contains only $G_{M}^{{{\kern 1pt} 2}}$. Averaging and summing Eq. (7) over the polarizations of the initial and final protons yields another representation [19, 20] for the Rosenbluth cross section (1), ${{\sigma }_{R}} = d\sigma {\text{/}}d{{\Omega }_{e}}$, in the form

$${{\sigma }_{R}} = {{\sigma }^{{ \uparrow \uparrow }}} + {{\sigma }^{{ \downarrow \uparrow }}}.$$

(11)

Therefore, the physical meaning of the representation of Rosenbluth formula (1) as the sum of two terms, one containing only $G_{E}^{{ 2}}$ and the other containing only $G_{M}^{{ 2}}$, is that it is the sum of the cross sections without (${{\sigma }^{{ \uparrow \uparrow }}}$) and with (${{\sigma }^{{ \downarrow \uparrow }}}$)proton spin flip in the case where the initial (at rest) proton is fully polarized along the direction of motion of the final proton. It is often stated in the literature, including textbooks on physics of elementary particles, that SFFs are used simply for convenience, because they make the Rosenbluth formula simple and concise. Since these formal conclusions about the advantages of using the SFFs can be found, in particular, in well-known monographs published many years ago [25, 26], they are considered as undoubtful and still reproduced in the literature (see, e.g., [27]).

Cross section (7) can be presented in the form

$$d{{\sigma }_{{{{\delta }_{1}},{{\delta }_{2}}}}}{\text{/}}d{{\Omega }_{e}} = (1 + {{\delta }_{2}}{{\delta }_{f}})({{\sigma }^{{ \uparrow \uparrow }}} + {{\sigma }^{{ \downarrow \uparrow }}}),$$

(12)

$${{\delta }_{f}} = {{\delta }_{1}}({{R}_{\sigma }} - 1){\text{/}}({{R}_{\sigma }} + 1),$$

(13)

$${{R}_{\sigma }} = {{\sigma }^{{ \uparrow \uparrow }}}{\text{/}}{{\sigma }^{{ \downarrow \uparrow }}},$$

(14)

where ${{\delta }_{f}}$ is the degree of the longitudinal polarization of the final proton. If the initial proton is fully polarized (${{\delta }_{1}} = 1$), ${{\delta }_{f}}$ coincides with the conventional definition of the polarization asymmetry:

$$A = ({{R}_{\sigma }} - 1){\text{/}}({{R}_{\sigma }} + 1).$$

(15)

As follows from (8), the ratio of the cross sections without and with proton spin flip, ${{R}_{\sigma }}$ (14), can be expressed in terms of the experimentally measurable value $R \equiv {{\mu }_{p}}{\kern 1pt} {{G}_{E}}{\text{/}}{{G}_{M}}$:

$${{R}_{\sigma }} = \frac{{{{\sigma }^{{ \uparrow \uparrow }}}}}{{{{\sigma }^{{ \downarrow \uparrow }}}}} = \frac{\varepsilon }{{{{\tau }_{p}}}}{\kern 1pt} \frac{{G_{E}^{2}}}{{G_{M}^{2}}} = \frac{\varepsilon }{{{{\tau }_{p}}{\kern 1pt} \mu _{p}^{2}}}{\kern 1pt} {{R}^{2}}.$$

(16)

To use the standard notation, Eq. (13) for the degree of longitudinal polarization of the final proton can be rewritten as follows:

$${{P}_{r}} = {{P}_{t}}({{R}_{\sigma }} - 1){\text{/}}({{R}_{\sigma }} + 1),$$

(17)

where ${{\delta }_{f}}$ and ${{\delta }_{1}}$ are replaced with ${{P}_{r}}$ and ${{P}_{t}}$, respectively.

Formula (17) makes it possible to express the R ratio in terms of ${{P}_{r}}{\text{/}}{{P}_{t}}$. Indeed, having inverted the relation in (17), we arrive at

$${{R}^{2}} = \mu _{p}^{2}{\kern 1pt} \frac{{{{\tau }_{p}}}}{\varepsilon }\frac{{1 + {{R}_{p}}}}{{1 - {{R}_{p}}}},\quad {{R}_{p}} = \frac{{{{P}_{r}}}}{{{{P}_{t}}}}.$$

(18)

The obtained Eq. (18) allows one to derive ${{R}^{2}}$ from the results of experiments on measuring the polarization transfer to the proton, ${{P}_{r}}$, in the process $e\vec {p} \to e\vec {p}$ when the initial (at rest) proton is partially polarized along the direction of motion of the detected recoil proton.

The results of the numerical calculations of the polarization transfer ${{P}_{r}}$ to the proton (17) as a function of the proton scattering angle both with preserved scaling (i.e., in the case of the dipole dependence ($R = {{R}_{d}}$)) and with scaling violated are presented below; two parameterizations ($R = {{R}_{j}}$ and $R = {{R}_{k}}$) are considered:

$${{R}_{d}} = 1,$$

(19)

$$R_{j}^{{ - 1}} = 1 + 0.1430{\kern 1pt} {{Q}^{2}} - 0.0086{\kern 1pt} {{Q}^{4}} + 0.0072{\kern 1pt} {{Q}^{6}},$$

(20)

where the expression for ${{R}_{j}}$ (20) was proposed in [24]; ${{R}_{k}}$ corresponds to the Kelly parameterization [23]; the corresponding formulas are omitted.

KINEMATICS OF THE PROCESS

Let us consider the dependences of the energies of the final electrons and protons on the energy of the initial electron beam and the electron and proton scattering angles in the laboratory reference frame, where ${{q}_{1}} = (M,{\mathbf{0}})$. Using the 4-momentum conservation law ${{p}_{1}} + {{q}_{1}} = {{p}_{2}} + {{q}_{2}}$, we obtain expressions for the scattered electron energy ${{E}_{2}}$ and the squared 4-momentum transfer to the proton ${{Q}^{2}} = - {{({{q}_{1}} - {{q}_{2}})}^{2}}$ as functions of the electron scattering angle ${{\theta }_{e}}$:

$${{E}_{2}} = {{E}_{1}}{\text{/}}(1 + \frac{{{{E}_{1}}}}{M}{\kern 1pt} (1 - \cos ({{\theta }_{e}})),$$

(21)

$${{Q}^{2}} = 2E_{1}^{2}(1 - \cos ({{\theta }_{e}})){\text{/}}\left( {1 + \frac{{{{E}_{1}}}}{M}(1 - \cos ({{\theta }_{e}})} \right),$$

(22)

where the ${{\theta }_{e}}$ is the angle between the vectors ${{{\mathbf{p}}}_{1}}$ and ${{{\mathbf{p}}}_{2}}$, $\cos ({{\theta }_{e}}) = {{{\mathbf{p}}}_{1}}{{{\mathbf{p}}}_{2}}{\text{/|}}{{{\mathbf{p}}}_{1}}{\kern 1pt} ||{\kern 1pt} {{{\mathbf{p}}}_{2}}{\text{|}}$.

The final electron energy ${{E}_{2}}$ and proton energy ${{E}_{{2p}}}$ are related to ${{Q}^{2}}$ in the laboratory reference frame:

$${{E}_{2}} = {{E}_{1}} - {{Q}^{2}}{\text{/}}2M,\quad {{E}_{{2p}}} = M + {{Q}^{2}}{\text{/}}2M,$$

(23)

$$\begin{gathered} {{E}_{2}} = {{E}_{1}} - 2M{{\tau }_{p}},\quad {{E}_{{2p}}} = M(1 + 2{{\tau }_{p}}), \\ {{\tau }_{p}} = {{Q}^{2}}{\text{/}}4{{M}^{2}}. \\ \end{gathered} $$

(24)

The dependence of ${{E}_{{2p}}}$ and ${{Q}^{2}}$ on the proton scattering angle ${{\theta }_{p}}$, which is the angle between the vectors ${{{\mathbf{p}}}_{1}}$ and ${{{\mathbf{q}}}_{2}}$, $\cos ({{\theta }_{p}}) = {{{\mathbf{p}}}_{1}}{{{\mathbf{q}}}_{2}}{\text{/|}}{{{\mathbf{p}}}_{1}}{\kern 1pt} ||{\kern 1pt} {{{\mathbf{q}}}_{2}}{\text{|}}$, has the form

$${{E}_{{2p}}} = M{\kern 1pt} \frac{{{{{({{E}_{1}} + M)}}^{2}} + E_{1}^{{{\kern 1pt} 2}}\mathop {\cos }\nolimits^2 ({{\theta }_{p}})}}{{{{{({{E}_{1}} + M)}}^{2}} - E_{1}^{{{\kern 1pt} 2}}\mathop {\cos }\nolimits^2 ({{\theta }_{p}})}},$$

(25)

$${{Q}^{2}} = \frac{{4{{M}^{2}}E_{1}^{{{\kern 1pt} 2}}\mathop {\cos }\nolimits^2 ({{\theta }_{p}})}}{{{{{({{E}_{1}} + M)}}^{2}} - E_{1}^{{{\kern 1pt} 2}}\mathop {\cos }\nolimits^2 ({{\theta }_{p}})}}.$$

(26)

The inverse relations between $\cos ({{\theta }_{e}})$, $\cos ({{\theta }_{p}})$ and ${{E}_{2}}$, ${{E}_{{2p}}}$ can be written as

$$\cos ({{\theta }_{e}}) = 1 - \frac{{{{Q}^{2}}}}{{2{{E}_{1}}{{E}_{2}}}} = 1 - \frac{{M{{Q}^{2}}}}{{{{E}_{1}}(2M{{E}_{1}} - {{Q}^{2}})}},$$

(27)

$$\cos ({{\theta }_{p}}) = \frac{{{{E}_{1}} + M}}{{{{E}_{1}}}}\sqrt {\frac{{{{\tau }_{p}}}}{{1 + {{\tau }_{p}}}}} .$$

(28)

In elastic process (3) the electron scattering angle ${{\theta }_{e}}$ changes from 0° to 180°, while ${{Q}^{2}}$ changes in the range of $0\;\leqslant \;{{Q}^{2}}\;{\kern 1pt} \leqslant \;Q_{{\max }}^{2}$ ($0\;\leqslant \;{{\tau }_{p}}\;\leqslant \;{{\tau }_{{\max }}}$), where

$$Q_{{\max }}^{2} = \frac{{4ME_{1}^{{{\kern 1pt} 2}}}}{{(M + 2{{E}_{1}})}},\quad {{\tau }_{{\max }}} = \frac{{E_{1}^{{{\kern 1pt} 2}}}}{{M(M + 2{{E}_{1}})}}.$$

(29)

Let us write the following useful relation:

$$\sqrt {\frac{{{{\tau }_{{\max }}}}}{{1 + {{\tau }_{{\max }}}}}} = \frac{{{{E}_{1}}}}{{M + {{E}_{1}}}}.$$

(30)

According to Eq. (22), at ${{\theta }_{e}} = 0$ we have ${{Q}^{2}} = 0$ and ${{\tau }_{p}} = 0$. However, if follows from Eq. (28) that $\cos ({{\theta }_{p}}) = 0$ in this case, which corresponds to proton scattering by 90°.

In the case of electron backscattering $({{\theta }_{e}} = 180^\circ )$, when ${{\tau }_{p}} = {{\tau }_{{\max }}}$, it follows from Eqs. (28) and (30) that $\cos ({{\theta }_{p}}) = 1$ and ${{\theta }_{p}} = 0^\circ$. Thus, the electron scattering by an angle ranging from 0° to 180° ($0^\circ \;\leqslant \;{{\theta }_{e}}\;\leqslant \;180^\circ$) leads to a change in the proton scattering angle from 90° to 0°.

The results of calculating the dependence of the electron scattering angle ${{\theta }_{e}}$ and proton scattering angle ${{\theta }_{p}}$ on the squared momentum transfer ${{Q}^{2}}$ to the proton at the electron beam energies used in SANE’s experiment [16], ${{E}_{1}} = 4.725$ and 5.895 GeV, are plotted in Fig. 1. The lines with marks ${{\theta }_{{e4}}},{{\theta }_{{p4}}}$ and ${{\theta }_{{e5}}},{{\theta }_{{p5}}}$ correspond to these plots.

Fig. 1.

(Color online) Electron scattering angle ${{\theta }_{e}}$ and proton scattering angle ${{\theta }_{p}}$ versus ${{Q}^{2}}$ at the electron beam energies used in the experiment [16]. The ${{\theta }_{{e4}}},{{\theta }_{{p4}}}$, and ${{\theta }_{{e5}}},{{\theta }_{{p5}}}$ lines are plotted for ${{E}_{1}} = 4.725$ and 5.895 GeV.

The data on the electron and proton scattering angles (in radians) at electron beam energies ${{E}_{1}} = 5.895$ and 4.725 GeV and ${{Q}^{2}} = 2.06$ and 5.66 GeV² are listed in Table 1, which contains also the values of $Q_{{\max }}^{2}$ (29) for the maximally possible ${{Q}^{2}}$ values at ${{E}_{1}} = 5.895$ and 4.725 GeV.

Table 1. Electron scattering angle ${{\theta }_{e}}$ and proton scattering angle ${{\theta }_{p}}$ (in radians) in the kinematics of experiment [16]

POLARIZATION OF THE VIRTUAL PHOTON IN THE $ep \to ep$ PROCESS

The $\varepsilon$ value entering the expression for the Rosenbluth cross section,

$$\varepsilon = (1 + 2(1 + {{\tau }_{p}}){{\tan }^{2}}({{\theta }_{e}}{\text{/}}2){{)}^{{ - 1}}}$$

(31)

with the range of variation $0\;\leqslant \;\varepsilon \;\leqslant \;1$ is generally identified in the literature with the degree of longitudinal polarization of the virtual photon. Sometimes it is also referred to as the polarization parameter or simply the virtual photon polarization. The physical meaning of the ε value is rarely understood correctly; in this context we should the absolutely correct words from [28]: “Let us introduce another set of kinematical variables: ${{Q}^{{{\kern 1pt} 2}}}$, and the degree of the linear polarization of the virtual photon, ε.”

Expression (31) for ε is a function of the electron scattering angle ${{\theta }_{e}}$. An expression for ε, which differs from (31) and makes it possible to calculate the dependences of the quantities of interest on, e.g., ${{Q}^{2}}$ or the proton scattering angle ${{\theta }_{p}}$, is given below; it was derived using the results of [5]:

$${{\varepsilon }^{{ - 1}}} = 1 + \frac{{{{{({{E}_{1}} - {{E}_{2}})}}^{2}} + 2({{E}_{1}} - {{E}_{2}})M}}{{2{{E}_{1}}{{E}_{2}} - ({{E}_{1}} - {{E}_{2}})M}}.$$

(32)

Here, ${{E}_{1}},{{E}_{2}}$ are the energies of the initial and final electrons, respectively. Note that Eqs. (23) and (24) must be used for ${{E}_{2}}$; they depend explicitly on only ${{Q}^{2}}$; in turn, the dependence of ${{Q}^{2}}$ on the angles ${{\theta }_{e}}$ and ${{\theta }_{p}}$ is determined by Eqs. (22) and (26).

The dependence of the degree of linear (transverse) polarization ε (32) of the virtual photon on the squared momentum transfer to the proton, ${{Q}^{2}}$, at the electron beam energies used in SANE’s experiment [16] is presented in Fig. 2.

Fig. 2.

(Color online) ${{Q}^{2}}$-dependence of the degree of linear polarization of the virtual photon, ε (32), for the electron beam energies of 4.725 and 5.895 GeV, used in the experiment [16].

It follows from Fig. 2 that $\varepsilon$ is a function of ${{Q}^{2}}$, which decreases from 1 to 0. In the case of electron scattered forward (${{\theta }_{e}} = 0^\circ$), when ${{Q}^{2}} = 0$, $\varepsilon = 1$; for a backscattered electron (${{\theta }_{e}} = 180^\circ$), when ${{Q}^{2}} = Q_{{\max }}^{2}$, $\varepsilon = 0$. The $Q_{{\max }}^{2}$ values for the energies ${{E}_{1}} = 4.725$ and 5.895 GeV are listed in Table 1; they amount to 8.066 and 10.247 GeV², respectively. Specifically at these points, the lines in Fig. 2 intersect the abscissa axis.

Figure 3 presents the dependence of the degree of linear polarization of the virtual photon (ε) on the electron and proton scattering angles (${{\theta }_{e}}$ and ${{\theta }_{p}}$, respectively) at the electron beam energies used in SANE’s experiment [16]. Note that the angle ${{\theta }_{e}}$ in the left panel of Fig. 3 changes from 0° to 180°, while in the right panel ${{\theta }_{p}}$ changes from 90° to 0°. This order of counting the angles ${{\theta }_{e}}$ and ${{\theta }_{p}}$ corresponds to the range of variation $0\;\leqslant \;{{Q}^{2}}\;{\kern 1pt} \leqslant \;Q_{{\max }}^{2}$ for each plot.

Fig. 3.

(Color online) Degree of linear polarization of the virtual photon, ε, versus the (left panel) electron scattering angle ${{\theta }_{e}}$ and (right panel) proton scattering angle ${{\theta }_{p}}$ (in degrees) at the electron beam energies of 5.895 and 4.725 GeV, used in the experiment [16].

The following regularities can be established based on the plots in Fig. 3: a smaller (larger) ε value corresponds to a higher electron beam energy ${{E}_{1}}$ for the same angle ${{\theta }_{e}}$ (${{\theta }_{p}}$).

ANGULAR DEPENDENCE OF THE POLARIZATION TRANSFER TO THE PROTON IN THE $e\vec {p} \to e\vec {p}$ PROCESS

In the laboratory reference frame, the degree of the longitudinal polarization transfer from the initial to the final proton in process (3) in the case of a proton target partially polarized along the direction of motion of detected recoil proton is determined by Eq. (17). Currently, the experiment aimed at measuring this parameter appears to be quite real, because such a target with a high degree of polarization,${{P}_{t}} = (70 \pm 5)$%, was in principle developed and even used in SANE’s experiment [16]. For this reason it would be most expedient to perform the proposed experiment on the facility used in [16] at the same value ${{P}_{t}} = 0.70$, electron beam energies ${{E}_{1}} = 4.725$ and 5.895 GeV, and squared momentum transfers to the proton ${{Q}^{2}} = 2.06$ and 5.66 GeV². The difference between the proposed experiment and the experiment [16] is that the electron beam must be unpolarized, and the detected recoil proton with longitudinal polarization must move strictly along the spin quantization axis of the proton target. This condition stems from the requirements imposed on the spin quantization axis for both the initial and final protons (5). The procedure of measuring the degrees of longitudinal and transverse polarizations of the final proton was developed and applied in the experiments [8–13]. To derive the $R$ ratio (18) in the proposed experiment, one must only measure the degree of longitudinal polarization of the recoil proton, which is an advantage in comparison with the method [3] used in [8–13].

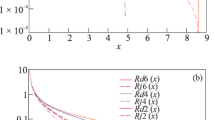
The calculated dependences of the longitudinal polarization transfer to the proton, ${{P}_{r}}$ (17), on the proton scattering angle ${{\theta }_{p}}$ for the electron beam energies of 5.895 and 4.725 GeV and for ${{P}_{t}} = 0.70$ are plotted in Fig. 4. Figure 4a shows the dependence in the entire range of variation in the angles ${{\theta }_{p}} \in (90^\circ ,0^\circ )$. In Fig. 4b the range of variation ${{\theta }_{p}} \in (47^\circ ,18^\circ )$ corresponds to the kinematics of the experiment [16], where 2.06 GeV² ⩽ ${{Q}^{2}}{\kern 1pt}$ ⩽ 5.66 GeV² (see Table 1). The $Pd5$, $Pk5$, and $Pj5$ ($Pd4$, $Pk4$, and $Pj4$) lines correspond to the electron beam energy ${{E}_{1}} = 5.895$ (${{E}_{1}} = 4.725$) GeV. In turn, the $Pd5$ and $Pd4$ lines were plotted for $R = {{R}_{d}}$ (19) for the case of dipole dependence; the $Pk5$ and $Pk4$ lines correspond to the Kelly parameterization [23] ($R = {{R}_{k}}$); and the $Pj5$ and $Pj4$ lines were plotted for $R = {{R}_{j}}$ (20) in the case of the Qattan parameterization [24].

Fig. 4.

(Color online) (a) Dependence of ${{P}_{r}}$ (17) on the proton scattering angle ${{\theta }_{p}}$ for the ${{E}_{1}}$ and ${{P}_{t}}$ values used in the experiment [16] in the entire range of variation in the angle ${{\theta }_{p}} \in (90^\circ ,0^\circ )$. (b) The same dependence in the range ${{\theta }_{p}} \in (47^\circ ,18^\circ )$, in which 2.06 GeV² ⩽ ${{Q}^{2}}{\kern 1pt}$ ⩽ 5.66 GeV². The $Pd$, $Pj$, and $Pk$ lines correspond to the dipole dependence (19), the Qattan parameteriza-tion (20) [24], and the Kelly parameterization [23].

It follows from the plots in Fig. 4 that the polarization transfer to the proton depends fairly strongly on the type of the R parameterization. In the case of SFF scaling violation, i.e., at $R = {{R}_{k}}$ and $R = {{R}_{j}}$, it essentially increases in magnitude in comparison with the case of dipole dependence, when $R = {{R}_{d}}$; the following inequalities are valid for all ${{\theta }_{p}}$ in this case: ${\text{|}}Pd5{\text{|}} < {\text{|}}Pk{\text{5|}} < {\text{|}}Pj5{\text{|}}$ and ${\text{|}}Pd4{\text{|}} < {\text{|}}Pk4{\text{|}} < {\text{|}}Pj4{\text{|}}$. Thus, the $Pk$ lines for the Kelly parameterization [23] occupy an intermediate position between $Pd$ and $Pj$.

To estimate quantitatively the difference between $Pj$, $Pk$, and $Pd$, Table 2 was compiled, which contains the degrees of the longitudinal polarization of the final proton, $Pj5$, $Pd5$, $Pj4$, $Pd4$, $Pk5$, and $Pk4$, and their relative differences ${{\Delta }_{{dj}}}$ and ${{\Delta }_{{dk}}}$ (in percent) at two electron beam energies (5.895 and 4.725 GeV) and two ${{Q}^{2}}$ values (2.06 and 5.66 GeV²) (${{\Delta }_{{dj}}} = (Pj - Pd){\text{/}}Pj$, ${{\Delta }_{{dk}}} = (Pk - Pd){\text{/}}Pk$).

Table 2. Degree of longitudinal polarization of the recoil proton ${{P}_{r}}$ (17) at electron beam energies ${{E}_{1}} = 5.895$ and 4.725 GeV and values ${{Q}^{2}} = 2.06$ and 5.66 GeV². The values in the columns for $Pd$, $Pj$, and $Pk$ correspond to the dipole dependence (19), the Qattan parameterization (20) [24], and the Kelly parameterization [23]. The corresponding electron and proton scattering angles (in degrees) are given in the columns for ${{\theta }_{e}}$ and ${{\theta }_{p}}$

It follows from Table 2 that, at ${{Q}^{2}} = 2.06$ GeV², the relative difference between $Pj5$ and $Pd5$ is 16.6%; the difference between $Pj4$ and $Pd4$ is approximately the same: 16.1%. At ${{Q}^{2}} = 5.66$ GeV² this difference decreases to 9.1 and 6.4%, respectively.

The difference between ${{\Delta }_{{dj}}}$ and ${{\Delta }_{{dk}}}$ in Table 2 is small; it varies from 2 to 6%. This difference can be explained by the fact that the Kelly parameterization [23] was proposed in 2004, prior to the experiments [12, 13], whose results were taken into account in [24] and made it possible to obtain a more accurate parameterization.

CONCLUSIONS

Proceeding from the results of JLab’s polarization experiments on measuring the ratio of the Sachs form factors in the $\vec {e}p \to e\vec {p}$ process, using the Kelly [23] (2004) and Qattan [24] (2015) parameterizations for this ratio, in the kinematics of SANE’s experiment [16] (2020) on measuring the double spin asymmetry in the $\vec {e}\vec {p} \to ep$ process, a numerical analysis of the dependence of the longitudinal polarization transfer to the proton in the $e\vec {p} \to e\vec {p}$ process on the proton scattering angle was performed for the case where the initial (at rest) proton is partially polarized along the direction of motion of the detected recoil proton. It has been found that the polarization transfer to the proton is fairly sensitive to the parameterization of the ratio of the Sachs form factors, which opens possibilities for a new independent measurement of this ratio in the $e\vec {p} \to e\vec {p}$ process.

It follows from the calculations that the violation of the scaling of the Sachs form factors leads to a significant increase in the magnitude of the polarization transfer to the proton, ${\text{|}}{{P}_{r}}{\text{|}}$, as compared to the case of the dipole dependence; the ${\text{|}}{{P}_{r}}{\text{|}}$ value obtained with the Kelly parameterization [23] is between the results obtained for the dipole dependence and Qattan parameterization [24]. Obviously, the parameterization [24], being based on a wider set of experimental data in comparison with the Kelly parameterization, including, in particular, the results reported in [12, 13], is more accurate and objective and leads to small differences from the results obtained with the Kelly parameterization.