On Laser-Induced High-Order Wave Mixing and Harmonic Generation in a Graphene Quantum Dot

We present results of numerical investigations of high-order wave mixing/harmonic generation (HWM/HHG) with many-body interaction processes derived by a strong two-frequency circular laser field in a graphene quantum dot (GQD). The influence of the relative phase of such a laser field on the spectrum of high-order harmonics generated in the GQD is shown. This may allow controlling the polarization of the generated harmonics. The GQD is described by the nearest neighbor tight-binding (TB) model. The multiparticle interaction is considered in an extended Hubbard approximation. We solve quantum kinetic equations in on-site representations for charged carriers by method have already applied by us, and obtain a general formula for high-order wave mixing/harmonic generation processes in GQD. The considerable enhancement of the HWM/HHG yield due to the matching of the symmetries of the light-wave–dot system takes place for the GQD with the particular group symmetry. The analysis of obtained results confirms enough efficiency of HWM/HHG in GQDs of the triangular and hexagonal shapes with zigzag edges at certain phases of a two-frequency circular laser field.

With the advent of lasers, it is growing interest to the main processes of the interaction of intense laser fields with crystals considered in nonlinear optics and nano-optics. The latter is transformation of a few pump photons to a single photon of higher energy, higher harmonic generation, or, in general, higher-order wave mixing: sum-difference-frequency generation [1]. The high harmonic generation (HHG) [2] is a highly nonperturbative process that goes beyond the nonlinear optics regimes. Up to the past decade, a study has focused on HHG in atomic and molecular gases [3]. Newly began to extend HHG to two-dimensional (2D) crystals and nanostructures, such as semimetallic graphene. The unique electronic and optical properties of graphene as an effective nonlinear optical material has been discussed in many theoretical [4–21] and experimental [22, 23] studies that consider various extreme nonlinear optical effects, in particular, high-order wave mixing (HWM)/HHG, which takes place in strong coherent radiation fields in the multiphoton regime at excitation of such nanostructures [24]. Indeed, the zero bandgap of the monolayer semimetal graphene limits the pristine graphene applicability in contrast to, for example, bilayer graphene [25]. For many nonlinear effects, the graphene energy gapless is the fundamental restriction, particularly for valleytronics. The latter is are impossible due to the inversion symmetry of such a system [26]. In [27] light-induced valley-selective excitations are demonstrated, and it has expected the significant valley-selective HHG in pristine graphene by using the combination of two counter-rotating circularly polarized fields, the fundamental and its second harmonic the so-called bicircular laser field. On the other hand, the problem of a zero energy gap in graphene also has been solved by decreasing the lateral size of graphene [28]. Among carbon nanostructures, there are of interest as a nonlinear medium the graphene nanoribbons [28, 29], graphene-like quantum dots, such as closed-convex fullerenes of different basic symmetry [20, 21], and graphene quantum dots (GQDs) of various finite sizes. The graphene nanostructure can be characterized by whether the sublattice symmetry is reserved. GQD has a gap that can be controlled by its lateral size, shape, and type of edge [28, 30, 31]. At the same time, such nanostructure exhibits optical properties that are fundamentally different from those of the pristine graphene [32, 33], and the GQDs have the same outstanding properties as the monolayer graphene [4]. The advantage of GQDs over graphene nanoribbons [34, 35] is the limitation of quasiparticles in space. Since the space limitation prevents the propagation of the electron wave packet deposited into also one additional dimension and, therefore, it increases the efficiency of the HHG [36–39]. Thus, it is of interest to study the influence of the relative phase of a two-frequency circular laser field on the spectrum of generated high-order harmonics in a GQD. The matching of the symmetries of the light-wave–dot system can take place for the GQD with the particular group symmetry. The latter has been crucial for HHG yield and can enhance the rates of harmonic generation. It may be controlled by the relative phase difference between the two frequencies of the pump wave. This can make it possible to control the polarization of the generated harmonics, as is usually done with HHG in gases [40].

In this work, we consider the multiphoton HHG in the plane quasi zero-dimensional GQDs of the triangular and hexagonal shapes with zigzag edges driven by the effective two-frequency circular field created by the two counter-rotating circularly polarized fields of the intense coherent radiation. The role of the phase of a high-intensity two-frequency circular field on the HHG process in the GQD plane has been studied. The closed set of differential equations for the single-particle density matrix at the GQD-strong laser field multiphoton interaction is solved numerically in the scope of the microscopic theory. The Coulomb electron–electron interaction (EEI) is described in the Hubbard approximation. The obtained solutions indicate the significance of the influence of total pump wave symmetry on the nonlinear optical response by GQD, taking into account that quantum dots have different shapes with diverse point-group symmetries, and the multiphoton HHG rates will be controlled by the intense two-frequency circular coherent radiation relative phase.

We will study a neutral planar GQD bounded in the $xy$ plane. We will consider a strong electromagnetic (EM) wave propagating perpendicular to the $xy$ plane. In this case, the EM wave becomes a homogeneous quasi-periodic electric field, i.e., a two-frequency circular field with strength ${\mathbf{E}} = ({{E}_{x}},{{E}_{y}})$:

$$\begin{gathered} {{E}_{x}}\left( t \right) = f\left( t \right) \\ \times \;\left( {{{E}_{{01}}}\cos \left( {\omega t + \phi } \right) + {{E}_{{02}}}\cos \left( {2\omega t + \phi } \right)} \right), \\ \end{gathered} $$

(1)

$$\begin{gathered} {{E}_{y}}\left( t \right) = f\left( t \right) \\ \times \;\left( {{{E}_{{01}}}\sin \left( {\omega t + \phi } \right) - {{E}_{{02}}}\sin \left( {2\omega t + \phi } \right)} \right), \\ \end{gathered} $$

(2)

where ϕ is the two-frequency phase and ${{E}_{{01}}}$ and ${{E}_{{02}}}$ are the strength amplitudes of the two counter-rotating circularly polarized fields of the fundamental pump wave with corresponding carrier frequencies ω and $2\omega$, constructing the so-called “trefoil” [27], $f\left( t \right) = \mathop {\sin }\nolimits^2 \left( {\pi t{\text{/}}\mathcal{T}} \right)$ is the slowly varying envelope with the pulse duration $\mathcal{T}$. The latter is taken to be 20 wave periods: $\mathcal{T} = 40\pi {\text{/}}\omega$.

Next, we use the method already applied in [37, 38]. The initial density matrix will be calculated from the empirical tight-binding (TB) Hamiltonian, i.e., the TB Hamiltonian dressed by the Coulomb interaction [28]. This approach has been widely used in the strong field physics community [12, 21, 41–47]. Briefly, this suggestion is justified as follows. The free GQD Hamiltonian reads

$${{\widehat H}_{{\text{0}}}} = - \sum\limits_{i,j,\sigma } t_{{ij}}^{0}c_{{i\sigma }}^{\dag }{{c}_{{j\sigma }}} + \frac{1}{2}\sum\limits_{i,j} {{V}_{{ij}}}{{n}_{i}}{{n}_{j}} + \frac{U}{2}\sum\limits_{i\sigma } {{n}_{{i\sigma }}}{{n}_{{i\overline \sigma }}},$$

(3)

where the operators $c_{{i\sigma }}^{\dag }$, ${{c}_{{i\sigma }}}$ satisfy anticommutation rules. The electron density operator is ${{n}_{{i\sigma }}} = c_{{i\sigma }}^{\dag }{{c}_{{i\sigma }}}$ and ${{n}_{i}} = {{n}_{{i \uparrow }}} + {{n}_{{i \downarrow }}}$ is the total electron density for the site i. The first term in the free Hamiltonian (3) is the kinetic energy part of the TB Hamiltonian with the bare tunneling matrix elements $t_{{ij}}^{0}$. The second and third terms in Eq. (3) correspond to the EEI within the extended Hubbard approximation with inter-site $\sim {\kern 1pt} {{V}_{{ij}}}$ and on-site $\sim {\kern 1pt} U$ Coulomb repulsion energies. The inter-site Coulomb repulsion is described by the distance ${{d}_{{ij}}}$ between the nearest-neighbor pairs varied over the system: $\sim {\kern 1pt} {{V}_{{ij}}} = V{{d}_{{\min }}}{\text{/}}{{d}_{{ij}}}$ (${{d}_{{\min }}}$ is the minimal nearest-neighbor distance). The EEI interaction part in Eq. (3) contains products of four fermionic operators. We have treated Coulomb interaction in the scope of phenomenological Hartree–Fock approximation. Using the Hartree–Fock decomposition [28], the Hamiltonian (3) can be approximated as:

$$\begin{gathered} \widehat H_{{\text{0}}}^{{HF}} \simeq - \sum\limits_{i,j,\sigma } t_{{ij}}^{0}c_{{i\sigma }}^{\dag }{{c}_{{j\sigma }}} + U\sum\limits_i \left( {{{{\bar {n}}}_{{i \uparrow }}}{{n}_{{i \downarrow }}} + {{{\bar {n}}}_{{i \downarrow }}}{{n}_{{i \uparrow }}}} \right) \\ + \;\sum\limits_{i,j} {{V}_{{ij}}}{{{\bar {n}}}_{j}}{{n}_{i}} - \sum\limits_{i,j,\sigma } {{V}_{{ij}}}c_{{i\sigma }}^{\dag }{{c}_{{j\sigma }}}\left\langle {c_{{i\sigma }}^{\dag }{{c}_{{j\sigma }}}} \right\rangle , \\ \end{gathered} $$

(4)

where $\left\langle {c_{{i\sigma }}^{\dag }{{c}_{{j\sigma }}}} \right\rangle$ is the mean-field density matrix and ${{\bar {n}}_{{i\sigma }}} = \left\langle {c_{{i\sigma }}^{\dag }{{c}_{{i\sigma }}}} \right\rangle$. Now in Eq. (4) we have only the product of two fermionic operators and the Hamiltonian (4) can be written as

$$\widehat H_{{\text{0}}}^{{HF}} = - \sum\limits_{i,j,\sigma } {{t}_{{ij}}}\left( {\left\langle {c_{{i\sigma }}^{\dag }{{c}_{{j\sigma }}}} \right\rangle } \right)c_{{i\sigma }}^{\dag }{{c}_{{j\sigma }}}.$$

(5)

This is effectively a one-body TB Hamiltonian given with the renormalized transfer energy ${{t}_{{ij}}}$ that depends on the mean-field density matrix. One can define the ground state $\rho _{{0ij}}^{{\left( \sigma \right)}}$ density matrix self-consistently [45], and then calculate renormalized transfer energy ${{t}_{{ij}}}\left( {\rho _{{0ij}}^{{\left( \sigma \right)}}} \right)$ or apply a phenomenological approach [28]. That is, one can take ${{t}_{{ij}}}$ to be equal to experimentally measured hopping integral for graphene nanostructures and proceed to evaluate density matrix elements with respect to the ground state, i.e., the fully occupied valence band of the empirical TB Hamilto-nian (5). Note that this approximation is not valid for the systems with the ground state essentially different from the fully occupied valence band. For example, the excitonic condensate [45]. However, for the graphene nanostructures, the experimental evidence for such phenomena is absent. Hence, the free Hamiltonian is taken in the form

$$\widehat H_{{\text{0}}}^{{HF}} \simeq - \sum\limits_{\left\langle {i,j} \right\rangle \sigma } {{t}_{{ij}}}c_{{i\sigma }}^{\dag }{{c}_{{j\sigma }}} + U\sum\limits_i ({{\bar {n}}_{{i \uparrow }}} - {{\bar {n}}_{{0i \uparrow }}}){{n}_{{i \downarrow }}}$$

$$ + \;U\sum\limits_{i\sigma } ({{\bar {n}}_{{i \downarrow }}} - {{\bar {n}}_{{0i \downarrow }}}){{n}_{{i \uparrow }}} + \sum\limits_{\left\langle {i,j} \right\rangle } {{V}_{{ij}}}({{\bar {n}}_{j}} - {{\bar {n}}_{{0j}}}){{n}_{i}}$$

(6)

$$ - \;\sum\limits_{\left\langle {i,j} \right\rangle \sigma } {{V}_{{ij}}}c_{{i\sigma }}^{\dag }{{c}_{{j\sigma }}}\left( {\left\langle {c_{{i\sigma }}^{\dag }{{c}_{{j\sigma }}}} \right\rangle - {{{\left\langle {c_{{i\sigma }}^{\dag }{{c}_{{j\sigma }}}} \right\rangle }}_{0}}} \right).$$

In this representation, the initial value of the density matrix ${{\left\langle {c_{{i\sigma }}^{\dag }{{c}_{{j\sigma }}}} \right\rangle }_{0}}$ is calculated with respect to TB Hamiltonian (5) at the fixed ${{t}_{{ij}}}$. That is, in the static limit the Hartree–Fock Hamiltonian for EEI vanishes. Thus, the EEI in the Hartree–Fock approximation is relevant only for quantum dynamics initiated by the pump laser field. The light-GQD interaction is described in the length-gauge via the pure scalar potential:

$${{\widehat H}_{{{\text{int}}}}} = e\sum\limits_{i\sigma } {{{\mathbf{r}}}_{i}}{\mathbf{E}}\left( t \right)c_{{i\sigma }}^{\dag }{{c}_{{i\sigma }}},$$

with the position vector ${{{\mathbf{r}}}_{i}}$ and the elementary charge e. From the Heisenberg equation $i\hbar \partial \widehat L{\text{/}}\partial t = \left[ {\widehat L,\widehat H} \right]$, we will obtain evolutionary equations for the single-particle density matrix $\rho _{{ij}}^{{\left( \sigma \right)}} = \left\langle {c_{{j\sigma }}^{\dag }{{c}_{{i\sigma }}}} \right\rangle$. We will also assume that the system relaxes at a rate γ to the equilibrium $\rho _{{0ij}}^{{\left( \sigma \right)}}$ distribution. To describe a closed set of equations for the single-particle density matrix $\rho _{{ij}}^{{\left( \sigma \right)}}$, EEI will be considered under the Hartree–Fock approximation and the Hamiltonian (3) is approximated by (6). Thus, the following equation for the density matrix is obtained:

$$\begin{gathered} i\hbar \frac{{\partial \rho _{{ij}}^{{\left( \sigma \right)}}}}{{\partial t}} = \sum\limits_k \left( {{{\tau }_{{kj\sigma }}}\rho _{{ik}}^{{\left( \sigma \right)}} - {{\tau }_{{ik\sigma }}}\rho _{{kj}}^{{\left( \sigma \right)}}} \right) + \left( {{{V}_{{i\sigma }}} - {{V}_{{j\sigma }}}} \right)\rho _{{ij}}^{{\left( \sigma \right)}} \\ + \;e{\mathbf{E}}\left( t \right)\left( {{{{\mathbf{r}}}_{i}} - {{{\mathbf{r}}}_{j}}} \right)\rho _{{ij}}^{{\left( \sigma \right)}} - i\hbar \gamma \left( {\rho _{{ij}}^{{\left( \sigma \right)}} - \rho _{{0ij}}^{{\left( \sigma \right)}}} \right), \\ \end{gathered} $$

(7)

and the matrices ${{V}_{{i\sigma }}}$ and ${{\tau }_{{ij\sigma }}}$ are defined in terms of the density matrix $\partial \rho _{{ij}}^{{\left( \sigma \right)}}$ as

$${{V}_{{i\sigma }}} = \sum\limits_{j\alpha } {{V}_{{ij}}}\left( {\rho _{{jj}}^{{\left( \alpha \right)}} - \rho _{{0jj}}^{{\left( \alpha \right)}}} \right) + U\left( {\rho _{{ii}}^{{\left( {\bar {\sigma }} \right)}} - \rho _{{0ii}}^{{\left( {\bar {\sigma }} \right)}}} \right),$$

(8)

$${{\tau }_{{ij\sigma }}} = {{t}_{{ij}}} + {{V}_{{ij}}}\left( {\rho _{{ji}}^{{\left( \sigma \right)}} - \rho _{{0ji}}^{{\left( \sigma \right)}}} \right).$$

(9)

Next, we numerically diagonalize the TB Hamiltonian ${{\widehat H}_{0}}$. Note that EEI in the Hartree–Fock limit is included in empirical hopping integral between the nearest-neighbor atom ${{t}_{{ij}}}$ which is chosen to be close to experimental data ${{t}_{{ij}}} = 2.7\;{\text{eV}}$ [28]. For all calculations we have taken $V = 0.3U$ [48, 49]. We neglected the lattice vibrations in the Hamiltonian. With the numerical diagonalization, we find eigenstates ${{\psi }_{\mu }}\left( i \right)$ and eigenenergies ${{\varepsilon }_{\mu }}$ ($\mu = 0,1,...,N - 1$). The results of numerical diagonalization are shown in the corresponding figure. One can see that without tunneling, all energy levels degenerate. So, the tunneling removed the degeneracy and led to the formation of the band of valence states below the Fermi level, ${{\varepsilon }_{\mu }} = 0$, a band of the conduction states above the Fermi level, and a gap across the Fermi level (see also [28]). The quantum dynamics of the GQD in a periodically strong wave field is governed by a closed set of differential Eqs. (7), which should be solved with the proper initial conditions. We construct primarily a density matrix $\rho _{{0ij}}^{{\left( \sigma \right)}}$ via the filling of electron states in the valence band in accordance with the zero temperature Fermi–Dirac distribution $\rho _{{0ij}}^{{\left( \sigma \right)}} = \sum\nolimits_{\mu = N/2}^{N - 1} \psi _{\mu }^{ * }\left( j \right){{\psi }_{\mu }}\left( i \right)$, with the eigenstate ${{\psi }_{\mu }}\left( i \right)$ of the Hamiltonian $\widehat H_{0}^{{TB}}$. The equation of motion for the density matrix is solved by performing the time integration of Eq. (7) with the standard fourth-order Runge–Kutta algorithm. We will define the HHG spectrum evaluating by the F-ourier transformation ${\mathbf{a}}\left( \Omega \right)$ of the dipole acceleration ${\mathbf{a}}(t) = {{d}^{2}}{\mathbf{d}}{\text{/}}d{{t}^{2}}$. The dipole is defined as d(t) = $\left\langle {\sum\nolimits_{i\sigma } {{{\mathbf{r}}}_{i}}c_{{i\sigma }}^{\dag }{{c}_{{i\sigma }}}} \right\rangle$. We normalize the dipole acceleration by the factor ${{a}_{0}} = {{\bar {\omega }}^{2}}\bar {d},$ where $\bar {\omega } = 1\;{\text{eV/}}\hbar$ and $\bar {d} = 1$ Å. The power radiated at a given frequency is proportional to ${{\left| {{\mathbf{a}}\left( \Omega \right)} \right|}^{2}}$. The GQDs have the zigzag edges for all cases. We assume the excitation frequency is $\omega = 0.1\;{\text{eV/}}\hbar$, which is much smaller than the typical gaps $U \simeq 3\;{\text{eV}}$, $V \simeq 0.3U$. The relaxation rate is taken to be $\hbar \gamma$ = 50 meV. For the most calculations, the wave field given by Eqs. (1) and (2) is assumed to be two-frequency circular laser field. The phase of the wave is $\varphi = 0$ in almost all cases. Initially, the component ${\text{|}}{{a}_{x}}\left( \Omega \right){\text{|}}$ is plotted, the results for ${\text{|}}{{a}_{y}}\left( \Omega \right){\text{|}}$ are identical. The x axis is in the plane of Figs. 1 and 2, and it is directed along x to the right.

Fig. 1.

Schematic diagram of a two-frequency circular field of an EM wave at ϕ = (a) 0 and (b) 3π/2.

Fig. 2.

Schematic diagram of the lattice of the (a) triangular and (b) hexagonal GQDs with N = 97 and 96 atoms and zigzag edges, respectively. The distance between nearest neighbor atoms is $a \simeq 1.42{\kern 1pt}$ Å.

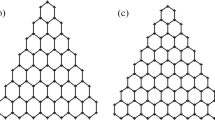
Figure 1 schematically demonstrates a two frequency circular EM field, Figs. 2 and 3, respectively, show the graphene lattice and the TB energy spectrum in the vicinity of the Fermi level, ${{\varepsilon }_{\mu }} = 0$, for triangular and hexagonal GQDs for similar numbers of carbon atoms. To compare the HHG rates, in further figures we have plotted all results for the harmonic emission spectra via the normalized atom number N of the dot. Further, we investigated the HHG spectra dependence on the relative phase the two-frequency circular laser field specified by Eqs. (1) and (2). Figures 4a and 4b show the dependence of ${\text{|}}{{a}_{x}}\left( \Omega \right){\text{|}}$ via two-frequency phase ϕ, respectively, for triangular and hexagonal GQDs. The wave frequencies are taken as $\omega = 0.1\;{\text{eV/}}\hbar$ and $\omega = 0.2\;{\text{eV/}}\hbar$, and two amplitudes of the field strength are ${{E}_{{01}}} = {{E}_{{02}}}$ = 0.1 V/Å. The total EM field is identical for $\phi = 0$ and $\phi = 2\pi$. As expected, the total harmonic probability is modulated as the “trefoil” of the two-frequency circular field is rotated. For unbounded in space graphene at the low-frequency pump wave, the HHG spectrum is isotropic with respect to the polarization vector of the two-frequency circular field rotation. For high frequencies, the isotropy vanishes, but due to the carbon hexagonal cell symmetry the optical response with respect to the polarization vector of the driven two-frequency circular field has a periodic character with a period $2\pi {\text{/}}3$, and the lower-order current-driven harmonics follow the expected pattern, maximizing when the electrons are driven into the steeper walls [27]. For GQD in the “trefoil” of the two-frequency circular field, we see a completely different picture. In this case, we have a strong anisotropy. The different ϕ lead to different HHG rates for the same harmonic. To clarity, Fig. 5 shows the HHG rate for the efficient harmonics H19 and H20 versus the two frequency phase. In particular, we have a maximum for H20 for the triangular GQD at the phase $\phi = 5\pi {\text{/}}12$, meanwhile for the hexagonal one the phases $\phi = 2\pi {\text{/}}3$, $5\pi {\text{/}}3$ are preferable. For the latter the spectrum is identical for $\phi = 0$ and $\phi = \pi$ due the threefold symmetry. Here, each π change in ϕ results in $2\pi {\text{/}}3$ rotation of the trefoil, yielding an equivalent configuration (as for unbounded graphene [27]). As Fig. 5 shows, for $\phi = 3\pi {\text{/}}2$ (the field configuration is given in Fig. 1b) for triangular GQD, the corresponding curve for H19, i.e., the $(3n + 1)$ harmonic following the polarization of the fundamental ω pulse, have the maximum, when symmetries of the “trefoil” of the two-frequency circular field and triangular GQD are coinciding, and the electrons are driven into the steeper walls by the “trefoil” of the two-frequency circular field. The H20 (as for $(3n + 2)$) harmonic following the polarization of the fundamental $2\omega$ pulse, have not the maximum at $\phi = 3\pi {\text{/}}2$ due to symmetry (see also [27]). As Fig. 5 shows, in both cases of GQDs the maximum at the defined phase for H19 will correspond to the minimum at the same phase for H20, and vice versa, due to the periodic character of the pump wave and energy conservation. Figure 4b shows that for any ϕ in hexagonal GQD the $3n$ harmonics are missing due to symmetry. We also verified that these results are independent of the specific directions of rotation of the two counter-rotating circularly polarized driven fields of the pump wave. That is, we have the same results with a simultaneous change in the helicity of both fields (see also [27]). Further, in order to clarify the main aspects of HHG of the effective two-frequency circular field in GQD, in Fig. 6 the component ${\text{|}}{{a}_{x}}\left( \Omega \right){\text{|}}$ is plotted at different amplitudes ${{E}_{{01}}},{{E}_{{02}}}$. In Fig. 7 the same is presented for hexagonal GQDs. As shown in Figs. 6 and 7, in a strong laser field, multiphoton harmonics will become equally significant for both triangular and hexagonal GQDs in the two-frequency circular field of the pump wave, and the cutoff energies will shift to the blue range. The considerable enhancement of the HHG spectrum due to the matching of the symmetries of the light-wave–dot system takes place as for the triangular, then the hexagonal GQD with the particular group symmetry. In both cases, the HHG spectra have a multistep plateau structure, which is associated with the excitations of energy eigenstates between the unoccupied energy levels and the occupied level [28]. The harmonic cutoff energy $\hbar \omega {{N}_{{{\text{cut}}}}}$ increases sufficiently compared to the HHG cutoff energies in a linearly polarized laser field when ${{E}_{{01}}} = 0$ or ${{E}_{{02}}} = 0$. Figures 6 and 7 show that in the latter linearly polarized wave for considered zigzag edge GQDs, due to the absence of the inversion symmetry, both odd and even harmonics are present in the HHG emission spectrum. In contradistinction with linearly polarized pump wave, as Fig. 7 demonstrates for hexagonal GQD in the two-frequency circular laser field, the HHG emission spectrum has the $(3n + 1)$ harmonics following the polarization of the fundamental ω pulse (left-handed circular polarization), whereas $(3n + 2)$ harmonics following the polarization of the second $2\omega$ pulse (right-handed circular polarization), while $3n$ harmonics are missing due to symmetry, just as in driven by two-frequency circular field atomic media [50, 51], and pristine graphene [27]. In Fig. 6 for triangular GQD the $3n$ harmonics are appearing due to inverse symmetry being broken. To show clearly the differences, Figs. 8a and 8b separately show the results for HHG emission spectra generated by a strong two-frequency circular field of pump wave in GQDs at a similar number of atoms respectively for triangular and hexagonal shapes. As Fig. 8 shows, for the considered two frequency phase $\phi = 0$ the HHG probabilities increase for hexagonal structures. In Fig. 8 we see the typical non-perturbative behavior of HHG with a multiple plateau structure. Note that the spectra shown in Fig. 8a, as well in Fig. 4, are especially richer. This is a consequence not only of the interference of the two different contributions, intraband and interband [21], but due to broken inverse symmetry in triangular GQD when the $3n$ harmonics appear. At that, Fig. 8 shows the dominant plateau shifted to the higher frequencies, in particular, for N = 97 and 96, we have an efficient multiphoton generation of harmonics from 15th to 40th and from 10th to 30th, respectively.

Fig. 3.

The eigenenergies in the (a) triangular and (b) hexagonal GQDs with N = 97 and 96 atoms and zigzag edges, respectively.

Fig. 4.

(Color online) Harmonic emission versus the two-frequency phase ϕ. The HHG emission spectra in the strong-field regime via dipole acceleration Fourier transformation ${{N}^{{ - 1}}}{\text{|}}{{a}_{x}}\left( \Omega \right){\text{|/}}{{a}_{0}}$ (in arbitrary units) versus the harmonic number and the two-frequency phase ϕ in the (a) triangular and (b) hexagonal GQDs with N = 97 and 96 atoms and zigzag edges, respectively. The wave frequencies are ω = 0.1 eV/ℏ and 2ω = 0.2 eV/ℏ and field strengths are ${{E}_{{01}}} = {{E}_{{02}}}$ = 0.1 V/Å. The EEI energies are $U = 3$ eV and $V = 0.9$ eV. The relaxation rate is ℏγ = 50 meV.

Fig. 5.

(Color online) Emission probability of (1, 2) the H20 harmonic in the (1) hexagonal and (2) triangular GQDs and (3, 4) the H19 harmonic in the (3) triangular and (4) hexagonal GQDs in the strong field regime via dipole acceleration Fourier transformation ${{N}^{{ - 1}}}{\text{|}}{{a}_{x}}\left( \Omega \right){\text{|/}}{{a}_{0}}$ (in arbitrary units) versus the two-frequency phase ϕ. The relaxation rate is ℏγ = 50 meV. The wave two frequencies are $\omega = 0.1\;{\text{eV/}}\hbar$, and field strengths are ${{E}_{{01}}} = {{E}_{{02}}}$ = 0.1 V/Å. The spectra are shown for typical moderate EEI energies $U = 3$ eV and $V = 0.9$ eV. The curves are presented in order as they intersect with the y axis.

Fig. 6.

(Color online) Same as in Fig. 4 but versus the pump wave harmonic number for the triangular GQD with N = 97 atoms at the phase $\phi = 0$ and at the field strengths (1) ${{E}_{{01}}} = {{E}_{{02}}}$ = 0.1 V/Å, (2) ${{E}_{{01}}}$ = 0.1 V/Å, ${{E}_{{02}}} = 0$, and (3) ${{E}_{{02}}}$ = 0.1 V/Å, ${{E}_{{01}}} = 0$.

Fig. 7.

(Color online) Same as in Fig. 6 but for the hexagonal GQD with $N = 96$ atoms.

Fig. 8.

Same as in Fig. 6 but for the two-frequency circular field at $\phi = 0$ in the (a) triangular and (b) hexagonal GQDs with N = 97 and 96 atoms and zigzag edges, respectively. In (b) the $3n$ harmonics missing due to symmetry in hexagonal GQD is driven by a two-frequency circular field.

To summarize, note that we have studied the influence of the effective two-frequency circular field of counter-rotating circularly polarized fields of fundamental pump wave on GQD, in particular, the phase of such a field. The microscopic theory has been used to describe the extreme nonlinear response of such nanostructure to intense coherent radiation. A closed system of differential equations for a one-particle density matrix in the multiphoton interaction of a GQD with a strong laser field is solved numerically for dots of the triangular and hexagonal shapes with zigzag edges. Numerical results show that, due to different sublattice symmetries, the same phases give different partial yields in the HHG spectra for triangular and hexagonal GQDs with a similar number of atoms. The phase $\phi \ne 0$ of the two-frequency circular field does not violate the inversion symmetry, and $3n$ harmonics are absent in the hexagonal GQD regardless of ϕ. The obtained results show that GQDs with the limitation of quasiparticles in space can serve as an effective medium for the generation of even and odd high-order harmonics in a two-frequency circular field of the wave with already moderate intensity. The probability of HHG increases at certain phases. The total HHG probability may be modulated as the “trefoil” of the two-frequency circular field is rotated. The harmonic cutoff energy $\hbar \omega {{N}_{{{\text{cut}}}}}$ increases sufficiently compared to the HHG cutoff energy in the linearly polarized laser field case. Due to the absence of inverse symmetry of the sublattice in triangular GQDs in all cases considered, as well as in hexagonal GQDs in a linearly polarized wave, harmonics of both odd and even order appear during generation, regardless of the two-frequency phase. For a two-frequency circular laser field interacting with a hexagonal GQD, we see a completely different picture. In this case, we have emission spectra of high harmonics, since $3n + 1$ are caused by the fundamental, $3n + 2$ are caused by the second harmonic of the pump wave, and $3n$ harmonics are absent due to the symmetry for the hexagonal GQD. Thus, we offer interesting systems for light-wave nanoelectronics and nonlinear optics. This is a potential way to increase the quantum yield and energy of emitted photons during HHG in graphene-like quantum dots, which should also allow one to control the polarization of the generated harmonics.