1 INTRODUCTION

The Lieb lattice is a two-dimensional square lattice of atoms of type A with atoms of type B located in the middle of the bonds between atoms of type A (see Fig. 1). The Lieb lattice is one of the simplest bipartite lattices, i.e., lattices with the sites that can be divided into two subsets A and B, where the nearest neighbors of sites A are sites B and vice versa. It was named after E.H. Lieb, who proved rigorous statements concerning the Hubbard model on bipartite lattices [1]. The Lieb lattice gained wide popularity owing to the presence of flat or nondispersive bands in its electron spectrum [2–5]. The absence of the kinetic energy of electrons in such bands leads to the essential role of arbitrarily small interactions between them and to the emergence of unusual correlated states of the electron system. The meaning of this statement can be clarified by comparing the physics of flat electron bands with the physics of flat bands of two-dimensional electrons in a high magnetic field. An experimental realization of the Lieb lattice is the CuO2 sublattice in high-temperature cuprate superconductors, which are also studied in numerous works (see, e.g., [6–9]). Similar structures, which can be referred to as distorted Lieb lattices, arise in water nanodroplets [10, 11]. Edge-centered cubic lattices, which are three-dimensional generalizations of the Lieb lattice, appear in hydrogen sulfide type high-Tc superconductors [12, 13] and as three-dimensional sublattices in various perovskites [14–16].

Fig. 1.
figure 1

(Color online) (Left) Original Lieb lattice and (right) the Lieb lattice arising as a result of the development of instability; the hopping integrals are indicated. Blue circles denote site atoms of type A and red circles are edge atoms of type B.

Full size image

Thus, the physics of compounds with the Lieb lattice is interesting and important for research. This work is aimed at the study of the electronic instability of the Lieb lattice. Analyzing the behavior of the electron and lattice energies, we demonstrate that the electron energy decreases owing to the displacements of the edge atoms from the bond centers. Under certain conditions, the increase in the elastic energy does not compensate the decrease in the electron energy; i.e., the Lieb lattice becomes unstable. Near such instability, lattices of this type are characterized by soft modes and anharmonic phonons. The development of instability results in a double-well shape of the potential energy of edge atoms as a function of displacements. Thus, the number of equilibrium positions of edge atoms on bonds is doubled, and a quantum tunneling of these atoms between equilibrium positions becomes possible. This gives rise to new excitations, quantum tunneling modes, which can be strongly coupled to the electron system.

Further, in Section 2, using the tight-binding method, we consider the structure of the electron spectrum of the Lieb lattice, its dependence on the displacements of the edge atoms along the bonds, and the presence of a flat band. In Section 3, we analyze the changes in the electron energy and in the energy of the ion lattice resulting from the displacements of edge atoms, and we find the conditions for the Lieb lattice instability. In Section 4, we discuss the experimental manifestations of the instability under study, its dependence on the lattice parameters, the relation between this instability and the Peierls instability [17], and the relation of the model under study to the one-dimensional polyethylene model or the Su–Schrieffer–Heeger (SSH) model [18, 19].

2 STRUCTURE OF THE ELECTRON SPECTRUM

The electron spectrum of any compound is determined not only by the structure of its crystal lattice but also by the valence states of atoms forming the lattice. Let us first consider a simple case, where atoms of type A and atoms of type B each have one valence state  \(\varphi _{i}^{{\text{A}}}\) and \(\varphi _{j}^{{\text{B}}}\), respectively. The solution of the Schrödinger equation is sought by the tight-binding method, i.e., in the form

$$\psi (r) = \sum\limits_{i \in {\text{A}}} {{a}_{i}}\varphi _{i}^{{\text{A}}}(\mathbf{r} - {\mathbf{r}_{i}}) + \sum\limits_{j \in {\text{B}}} {{b}_{j}}\varphi _{j}^{{\text{B}}}(\mathbf{r} - {\mathbf{r}_{j}}),$$
(1)

where \({{a}_{i}}\) and \({{b}_{i}}\) are the coefficients in the series expansion. The first and second sums are taken over the square lattice sites and lattice edges, respectively. Taking into account the hopping integrals only between the nearest neighbors, we obtain the following set of equations for the coefficients of the expansion:

$$({{\varepsilon }_{{\text{A}}}} - \varepsilon ){{a}_{i}} + \sum\limits_{j = 1}^4 {{t}_{{ij}}}{{b}_{j}} = 0,$$
(2)
$$({{\varepsilon }_{{\text{B}}}} - \varepsilon ){{b}_{j}} + \sum\limits_{j = 1}^2 {{t}_{{ij}}}{{a}_{i}} = 0.$$
(3)

Here, the sums are taken over the nearest neighbors, εA and εB are the energies of the respective lattice sites, and the hopping integrals are nonzero only for the nearest neighbors, \({{t}_{{ij}}} = {{t}_{{ji}}} = t\). All hopping integrals are the same only in the undistorted Lieb lattice, where the edge atoms are located exactly at the bond centers. Since our aim is to study the instability with respect to the displacement of the decorating atoms along the bonds, we assume the same absolute values of displacements of the decorating atoms and introduce two values of the hopping integrals, \({{t}_{{ij}}} = {{t}_{1}},{{t}_{2}}\), for the shortened and elongated bonds, respectively, i.e., \({{t}_{1}} > {{t}_{2}}\).

We begin to solve Eqs. (2) and (3) at the energy ε = εB. In this case, all equations (3) are satisfied at \({{a}_{i}} = 0\). Then, Eqs. (2) give N conditions for \(2N\) variables \({{b}_{j}}\); i.e., they lead to N linearly independent solutions for \({{b}_{j}}\). Thus, the energy ε = εB corresponds to an N-fold degenerate band (flat band). It is easy to understand its origin, because B atoms are effectively isolated under the condition \({{a}_{i}} = 0\) in the tight-binding approximation.

Then, at ε ≠ εB, using Eqs. (3) we can exclude the variables \({{b}_{j}}\) and obtain the equations only for the variables \({{a}_{i}}\):

$$\left( {{{\varepsilon }_{{\text{A}}}} + \frac{{{{\gamma }_{i}}}}{{\varepsilon - {{\varepsilon }_{{\text{B}}}}}} - \varepsilon } \right){{a}_{i}} + \frac{{{{t}_{1}}{{t}_{2}}}}{{\varepsilon - {{\varepsilon }_{{\text{B}}}}}}\sum\limits_{j \in i} {{a}_{j}} = 0.$$
(4)

Here, the sum is taken over the nearest neighbors of the ith site, and \({{\gamma }_{i}}\) are determined by the sums over the bonds adjacent to the ith site:

$${{\gamma }_{i}} = \sum\limits_{j \in i} t_{{ij}}^{2} = {{\alpha }_{i}}t_{1}^{2} + {{\beta }_{1}}t_{2}^{2},$$
(5)

where \({{\alpha }_{i}}\) and \({{\beta }_{i}}\) are natural numbers satisfying the condition \({{\alpha }_{i}} + {{\beta }_{i}} = 4\), i.e., in general, \({{\gamma }_{i}}\) may randomly have different values depending on the displacements of the decorating atoms.

The latter means that we deal with a difficult problem of determining the spectrum of a disordered system. However, it seems reasonable to assume that two atoms located at four bonds are displaced toward the site under study, and the other two atoms are displaced away from this site. This assumption is supported by an analogy with the physics of ice, in particular, with the first rule of ice: two protons are located near the oxygen ion, and two others are situated at some distance from it [4, 20, 21]. Physically, this rule is due to a decrease in the energy of the Coulomb interaction between ions. Under such assumption, all parameters \({{\gamma }_{i}}\) have the same value \(2t_{1}^{2} + 2t_{2}^{2}\). As a result, we arrive at a simpler model, which does not involve any disorder. Having this in mind, we accept below that the displacements of decorated atoms obey the ice rule; i.e., we use the condition \({{\gamma }_{i}} = 2t_{1}^{2} + 2t_{2}^{2}\) to determine the electron spectrum. The deviations from this condition can be treated as local perturbations of the site energy giving rise to the formation of local levels within the band gap, which will be considered elsewhere.

Using the condition based on the ice rules, we obtain from Eqs. (4) the following expressions for the dispersion laws in two energy bands:

$$\begin{gathered} {{\varepsilon }_{{{\text{c}}{\text{,v}}}}} = \frac{{{{\varepsilon }_{{\text{B}}}} + {{\varepsilon }_{{\text{A}}}}}}{2} \\ \pm \;\sqrt {{{{\left( {\frac{{{{\varepsilon }_{{\text{B}}}} - {{\varepsilon }_{{\text{A}}}}}}{2}} \right)}}^{2}} + 2t_{1}^{2} + 2t_{2}^{2} + 2{{t}_{1}}{{t}_{2}}(\cos {{k}_{x}} + \cos {{k}_{y}})} . \\ \end{gathered} $$
(6)

Here, we assume that εA < εB; then the minus and plus signs correspond to the lower (valence) and upper (conduction) bands, respectively. The band edges are given by the expressions

$${{\varepsilon }_{{{\text{c}}{\text{,v}}}}} = \frac{{{{\varepsilon }_{{\text{B}}}} + {{\varepsilon }_{{\text{A}}}}}}{2} \pm \sqrt {{{{\left( {\frac{{{{\varepsilon }_{{\text{B}}}} - {{\varepsilon }_{{\text{A}}}}}}{2}} \right)}}^{2}} + 2({{t}_{1}} - {{t}_{2}}{{)}^{2}}} ,$$
(7)

and the band gap width is

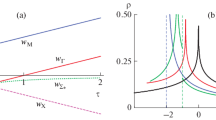
$${{\varepsilon }_{{\text{g}}}} = 2\sqrt {{{{\left( {\frac{{{{\varepsilon }_{{\text{B}}}} - {{\varepsilon }_{{\text{A}}}}}}{2}} \right)}}^{2}} + 2({{t}_{1}} - {{t}_{2}}{{)}^{2}}} .$$
(8)

Under the chosen condition εA < εB, the flat ε = εB band, as easily seen, is located within the band gap near the bottom of the conduction band. The electron energies as functions of the wave vector and the schematic density of states are shown in Figs. 2 and 3, respectively. Note that under the condition \({{t}_{1}} = {{t}_{2}}\), i.e., for the undistorted Lieb lattice, the flat band touches the bottom of the conduction band. Under the additional condition εA → εB, the band gap width tends to zero, and we obtain a semimetal with the flat band at the energy at which the conduction and valence bands touch each other. We can also demonstrate that the flat band in the case of the undistorted Lieb lattice \(({{t}_{1}} = {{t}_{2}})\) is preserved even taking into account the hoppings between the nearest neighbors in sublattice B (see the hopping integrals \({{t}_{3}}\) in Fig. 1). In the opposite case, i.e., under the condition \({{t}_{1}} \ne {{t}_{2}}\), this band exhibits a nonzero dispersion.

Fig. 2.
figure 2

(Color online) Example of the electron spectrum in the Lieb lattice. Band gaps become narrower with a decrease in the energy difference εB – εA and with a decrease in the difference of hopping integrals \({{t}_{1}} - {{t}_{2}}\). The dispersion increases with hopping integrals.

Full size image
Fig. 3.
figure 3

(Color online) Density of states corresponding to the spectrum shown in Fig. 2. The line within the band gap schematically represents the \(\delta \) function.

Full size image

3 ENERGIES OF THE ELECTRON AND ION SYSTEMS: INSTABILITY CONDITIONS

It can be seen from Eqs. (6) and (7) that the energy levels of the valence band become lower with the decrease in the displacements of the edge atoms, i.e., when t1 ≠ t2. Let us calculate the energy gain in the electron system as a function of the displacement of edge atoms. Assuming that all atoms are displaced by the same small distances x, we use the expressions for the hopping integrals \({{t}_{{1,2}}} = t \mp \alpha x\), where t, α > 0 and x < 0. Then, there are 3N valence electrons in the system, 2N of them completely fill the valence band, and N electrons fill half the flat band. The gain in the electron energy per unit cell due to the nonzero displacement of the edge atoms can be represented as the doubled integral of the valence band energy εv(k) over the occupied Brillouin zone. Without expansion of rather cumbersome expressions in terms of x2, the result can be represented in the form

$$\delta E(x) = - \frac{4}{{{{\pi }^{2}}}}\int\limits_0^{\pi /2} d{{q}_{x}}\int\limits_0^{\pi /2} d{{q}_{y}}[({{q}_{x}},{{q}_{y}},x) - f({{q}_{x}},{{q}_{y}},0)],$$
(9)
$$f({{q}_{x}},{{q}_{y}},x) = \sqrt {{{\Delta }^{2}} + 16{{t}^{2}}(\mathop {\cos }\nolimits^2 {{q}_{x}} + \mathop {\cos }\nolimits^2 {{q}_{y}}) + 16{{\alpha }^{2}}{{x}^{2}}(\mathop {\sin }\nolimits^2 {{q}_{x}} + \mathop {\sin }\nolimits^2 {{q}_{y}})} ,$$
(10)

where Δ = εB – εA. The first term of the expansion of Eq. (10) in terms of \({{x}^{2}}\) has the form

$$\delta {{E}_{1}} = - C{{x}^{2}},$$
(11)
$$C(\alpha ,\Delta ,t) = \frac{{32{{\alpha }^{2}}}}{{{{\pi }^{2}}}}\int\limits_0^{\pi /2} \int\limits_0^{\pi /2} \frac{{(\mathop {\sin }\nolimits^2 {{q}_{x}} + \mathop {\sin }\nolimits^2 {{q}_{y}})d{{q}_{x}}d{{q}_{y}}}}{{\sqrt {{{\Delta }^{2}} + 16{{t}^{2}}(\mathop {\cos }\nolimits^2 {{q}_{x}} + \mathop {\cos }\nolimits^2 {{q}_{y}})} }}.$$

The function \(C(\alpha ,\Delta ,t)\) can be explicitly calculated in different limiting cases, and its numerical values at arbitrary values of the arguments are illustrated in Fig. 4. Expressions (11) also demonstrate that the change in the electron energy at the displacement of edge atoms is always negative, which implies the electron instability of the Lieb lattice. The gain in the electron energy increases with the decrease in the difference Δ of the atomic energies and with the decrease in the hopping integral t. It also increases with α, which characterizes the dependence of the overlapping integral on the interatomic distance.

Fig. 4.
figure 4

(Color online) Integral in (11) versus the parameters Δ = εB – εA and t. The region corresponding to the maximum values of the integral is highlighted.

Full size image

While calculating the gain in electron energy (11), the kinetic energy of electrons and the energy of the interaction of electrons with the ionic core were taken into account. Using a phenomenological approach, we now consider the change in the energy of the ion system under the displacement of the edge atoms and write this energy in the form of the following sum of the first two terms of the power expansion in the displacement:

$$\delta {{E}_{2}}(x) = D{{x}^{2}} + F{{x}^{4}}.$$
(12)

Here, the constant F is positive, corresponding to the repulsion between A and B ions at extremely small distances between them, and the determination of the sign of the constant D is more complicated; we discuss it below in detail. First, we assume that \(D > 0\). These assumptions imply the stability of the Lieb lattice if only the energy of the ion system is taken into account. Then, using Eqs. (11) and (12), we find

$$\delta E = (D - C){{x}^{2}} + F{{x}^{4}},\quad {{x}_{ \pm }} = \pm \sqrt {\frac{{C - D}}{{2F}}} .$$
(13)

The first of these formulas demonstrates that the lattice is unstable at \(C > D\), whereas the second formula determines the equilibrium displacements of the edge atoms, when the electron subsystem induces instability.

The above assumption that D > 0 is based on the inclusion of the Coulomb interaction of the edge B ion only with the A nearest neighbors. However, the Coulomb interaction decreases slowly with increasing distance, and therefore, the Coulomb interaction of the B edge ion with more distant neighbors should also be taken into account because it can change the sign of the constant D. Indeed, it was shown in [22] that only the inclusion of the long-range interaction between edge ions without involving the electron energy can lead to the instability of the Lieb lattice or square ice lattice (in the terminology of [22]). The results obtained in [22] can also be interpreted in such a way that the inclusion of the long-range interaction between B ions makes a negative contribution to the coefficient of x2 in Eq. (12). In our opinion, the relation between the positive contribution of the interaction between the nearest neighbors and the negative contribution of the interaction between distant neighbors is close to the problem of the degeneracy of proton configurations that satisfy the ice rules [23–25].

Summarizing the above, we conclude that the inclusion of the long-range Coulomb interaction significantly reduces the positive constant D obtained from estimates of the interaction between the nearest neighbors. In this case, the contribution to the instability of the electron energy can become dominant, especially with an increase in the constant α and a decrease in the constants t and Δ. Thus, the inclusion of the long-range Coulomb interaction between ions only enhances the probability of emergence of an instability in the Lieb lattice.

4 DISCUSSION OF THE RESULTS

In the previous sections, we described the instability of the Lieb lattice caused by a decrease in the electron energy induced by displacements of the edge atoms along the bonds. In this section, we consider the effect of this instability on the physical characteristics of real materials, which can be more or less correctly described in terms of the Lieb lattice. We also discuss the relation of our model to other models and studies, in which the electron instability plays a significant role.

The best-known implementation of the Lieb lattice is the two-dimensional CuO2 sublattice of cuprate superconductors, and the most common interpretation for the superconducting transition temperature in these compounds involves soft phonon modes and anharmonic phonons related to vibrations of the atoms of this sublattice (see [9, 26, 27]). These papers contain numerous references to the experimental studies of soft phonon modes and anharmonic phonons, as well as various theoretical interpretations of the origin of these phonon features. However, all such theoretical interpretations differ from our model, which is actually based only on the topology of the Lieb lattice.

Note that almost all of our results can also be applied to a three-dimensional generalization of the Lieb lattice, namely, to a cubic lattice of sulfur ions with protons located at the centers of its edges (the chemical formula of this compound is H3S). Such a compound is produced at a high pressure and transforms to the superconducting state at temperatures above 200 K [12, 28]. In this case, a high superconducting transition temperature is also probably due to anharmonic phonons. Moreover, a transition to the state with an asymmetric hydrogen bond, i.e., to the state with displacements of protons from the bond center, is also observed in this case [12]. The presence of an asymmetric hydrogen bond implies a pronounced instability of the lattice. In this case, the formation of quantum tunneling modes due to the tunneling of protons along bonds is possible, leading to an interesting and important problem of the interaction of tunneling modes with electrons and their effect on superconductivity.

Superconductivity is not the only phenomenon in which the analyzed instability manifests itself. Indeed, instability can manifest itself not only in anharmonic phonons but also in static distortions. In this regard, it is worth discussing the relation of the instability under study to ferroelectricity. Ferroelectrics are usually classified into displacement- and order–disorder-type ferroelectrics. The first type includes a number of compounds with the perovskite structure, e.g., barium titanate BaTiO3 and lead zirconate PbZrO3. These compounds include three-dimensional TiO3 and ZrO3 lattices serving as sublattices in the corresponding crystals. They could be considered as three-dimensional generalizations of the Lieb lattice, to which our results can be easily adapted. They also exhibit a decrease in the energy if oxygen ions are displaced along the edges, which can be interpreted as the driving force of their ferroelectric characteristics. In the case of a pronounced instability, each edge ion has two stable equilibrium positions. The distribution of ions over these positions can be described by pseudospin variables within the Ising model, in which either an order–disorder or a ferroelectric transition occurs [29, 30].

The electron instability under study can cause the asymmetry of the hydrogen bond and disorder in the proton subsystem in many three-dimensional modifications of ice [21]. Moreover, it was shown in [10, 11] that square ice, which is close to the Lieb lattice, can be realized in ice nanodroplets. The difference is a rather strong deviation of protons, i.e., edge ions, from bond centers. These deviations can be considered as an experimental confirmation of the aforementioned instability.

Let us now determine the conditions under which instability manifests itself most clearly, i.e., the conditions under which the bonds are asymmetric and symmetric. As mentioned in the preceding section, the condition of a pronounced instability or a double-well potential has the form C > D, where D is determined by the elastic energy of the ion lattice (a phenomenological constant in our work), and C is given in Eqs. (11). It follows from Eqs. (11) that C increases with a decrease in Δ and t. This means that the role of the electron instability will be larger in compounds with close values of the energy of valence electrons (the maximum is attained if the energies are equal, Δ = 0). The value of t characterizes the hopping integrals between the nearest neighbors for the undistorted lattice. Correspondingly, the larger the distance between atoms, i.e., the lattice constant, the smaller the t value. The lattice constant can be varied in two ways: by a specific choice of atoms and by the applied pressure. In the latter case, if the instability at zero pressure is so pronounced that the bonds are asymmetric, then the lattice constant decreases with increasing pressure; hence, t increases and C decreases. At a sufficiently high pressure, one can expect a small effect of instability, and a transition to the symmetric phase with a single-well potential. Near the transition between the double-well and single-well potentials, the height of the potential barrier will be low, and the quantum tunneling of edge atoms and the formation of tunneling modes can be expected. In other words, the corresponding vibrations of edge atoms become anharmonic. Thus, the pressure is one of the parameters controlling the strength of instability.

With a decrease in Δ and in the distance between the two minima of the potential, i.e., with a decrease in t1 − t2, the gaps between the bands shown in Fig. 2 decrease. In the limiting case \(\Delta = 0\) and \({{t}_{1}} = {{t}_{2}}\), two bands with a pronounced dispersion should touch the flat zone. If the Fermi level of the system coincides with this energy, there are two types of electrons near the Fermi level: some electrons with a high density of states, but with a zero group velocity, and other electrons with a low density of states, but with a high group velocity. This situation is of interest both for the normal conductivity and for the formation of a superconducting state.

Then, according to Sections 2 and 3, the instability under study is obviously quite similar to the Peierls instability [17]; i.e., the latter could be treated in the framework of our model. In fact, our model can be considered as a generalization of the Peierls model for the two-dimensional case. The relation of our model to the one-dimensional model of polyethylene is also of interest. In the latter, there are two phases with the displacement of atoms to the left and to the right, and bound electron states that can carry an electric current under the applied electric field exist at the boundary of such phases. In our case, the ice rule implies the equality \({{\gamma }_{i}} = 2t_{1}^{2} + 2t_{2}^{2}\) (see Section 2). If the ice rule is violated, this equality becomes invalid, which can be considered as a local perturbation leading to the formation of bound states of electrons within the band gap. When the edge atoms hop along the bonds (in the case of asymmetric bonds), such a defect together with an electron moves across the sample; i.e., it can be a charge carrier similar to those in ice physics [21]. In this respect, such charge carriers can be considered as two-dimensional generalizations of charge carriers in the Su–Schrieffer–Heeger model [18].