An increase in the efficiency of the interaction between light radiation and matter is one of the fundamental problems of modern quantum technologies (see, e.g., [1]). Currently available materials allow strong and ultrastrong coupling at this interaction [2]. Strong matter–field coupling implies the periodic energy exchange between two-level systems (TLSs) such as atoms, quantum dots, and excitons and the quantized field of a cavity [3–5].

The strong-coupling regime appears if the single-photon Rabi frequency \(2{{g}_{0}}\) exceeds the spontaneous decay rate, dephasing rate, and losses in the cavity; modern experiments with cold atoms allow the observation of vacuum Rabi splitting reached with a single atom (see, e.g., [3]). However, the improvement of the collective matter–field coupling parameter is a more important practical problem for quantum informatics involving various physical systems of quantum information processing and transmission (see [6, 7]). The Rabi splitting frequency in this case depends on the collective coupling parameter \(g = \sqrt N {{g}_{0}}\) between TLSs and field, which demonstrates an increase in the field–matter coupling parameter by a factor of \(\sqrt N \), where N is the number of TLSs interacting with the single-mode cavity field. In this case, the effective Dicke spin, which can be assigned to the ensemble of TLSs, behaves as a giant quantum oscillator effectively coupled to one quantized mode described by the parameter g (see [8]).

Researchers have recently focused on obtaining the (collective) ultrastrong coupling regime of TLSs with the cavity field (cf. [2, 9, 10]). In particular, the ultrastrong coupling regime occurs after one bypass around a traditional Fabry–Perot cavity at the collective coupling of the ensemble TLSs to the quantized (multimode) field (see [2, 9, 11, 12]).

At the same time, a small volume of the cavity and a high dipole moment of TLSs make it possible to reach a high collective coupling parameter g or even g0, which can be comparable with the frequency ωph of the cavity field; i.e., g0/ωph ~ 0.01–1 [1]. The ultrastrong coupling regime with g0/ωph = 0.12 was experimentally achieved with superconducting flow qubits coupled to the mode of a transmission line resonator in the microwave frequency range [10]. The achievement of ultrastrong coupling of the field to the atomic or semiconductor TLSs is an important and very difficult problem because the parameter g0/ωph is very small, 10–6 and 10–3, respectively, in existing experiments (cf. [3, 13]).

In this work, to achieve ultrastrong coupling between the quantized field and matter, we propose for the first time to use certain topological properties of network structures. More precisely, we propose to organize an artificial structure (material) in the form of a graph (network), which allows ultrastrong coupling between the collective spin of ultrastrong TLSs located at nodes and modes of waveguides, which are edges of the graph (cf. [14]). We suggest that the topology of such a graph (network) corresponds to a power-law node degree distribution, which is widely used in information science to study various information processes in real networks [15]. In particular, hubs that can appear in such networks ensure much faster and reliable information transmission [16].

The main aim of this work is to determine the effect of the network architecture on the Rabi splitting and the appearance of a high-temperature phase transition to the superradiant state.

The phenomenon of superradiance is usually discussed in two limiting cases. First, superradiance is considered in significantly nonequilibrium systems including TLSs and a field under certain conditions for the characteristic times of relaxation and collective processes in a medium (see, e.g., [17–20]). Second, superradiance is considered as a result of a second order phase transition occurring in the thermodynamically equilibrium system consisting of TLSs and the quantized field (see, e.g., [21, 22]). Obviously, such a division is physically conditional because the total thermodynamic equilibrium in the system including TLSs and the quantized field is hardly possible. However, it is possible sometimes to obtain coupled states of atomic or exciton systems and the quantized field that are close in properties to thermodynamically equilibrium states and can demonstrate collective superradiance effects and/or Bose–Einstein condensation (cf. [13, 23, 24]). In this case, it is necessary to preliminarily prepare the medium and field for the observation of the phase transition, where the influence of weak relaxation processes on the effect itself is insignificant. This procedure is based on the thermalization of coupled states of matter and field (dressed states or polaritons) during which relaxation processes play an important role (see, e.g., [25, 26]). The discussed phase transition is well distinguishable in experiment from significantly nonequilibrium phase transitions (e.g., lasing), which can occur in the same system but at other pump parameters, difference between the populations of TLSs, etc. (see, e.g., [13, 27]). In this work, we consider the thermodynamically equilibrium phase transition to the superradiant state within the topological model of the coupling of TLSs to quantized radiation, which can be implemented by means of various physical systems having specificity in thermalization. The study of this specificity is an extensive theoretical and experimental problem and is beyond the scope of this work.

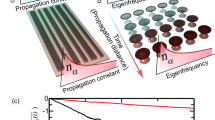
The proposed model consists of N TLSs that are localized at nodes of the graph, as shown in Fig. 1, and are in a thermodynamically equilibrium state at the temperature T. The number of edges kj connecting the jth node to other nodes is called the degree of this node.

Fig. 1.
figure 1

(Color online) Samples of network structures with power-law node degree (photon channel) distributions \(p(k) \propto {{k}^{{ - \gamma }}}\) with the power-law exponent γ = (a) 1.5, (b) 2.5, and (c) 5 shown in panel (d) on a log–log scale. The inset in panel (d) shows \(\langle k\rangle \) and ζ versus γ on a log–lin scale for the network architecture with N = 100 nodes and kmin = 2.

Full size image

Various physical implementations of the material with the graph architecture shown in Fig. 1 are possible. In particular, two-level atoms can be used as TLSs; they can be confined on the surface of a two-dimensional (photonic crystal) structure using the Casimir–Polder effect [28]. In this case, the corresponding confining potentials of individual atoms induced by the attractive van der Waals forces form an array of microcavities (cf. [29]). Coupling between atoms can be ensured by the same (photonic crystal) system of waveguides [30] or, e.g., using the technology of direct laser writing of waveguide structures, which is widely used currently to fabricate quantum (photon) chips (see, e.g., [31]). In this case, waveguides which have ultralow losses of 0.1 dB/cm serve as the edges of the graph. Another method to prepare aperiodic structures under consideration is based on the use of laser-induced microtraps for an ensemble of cold atoms (see, e.g., [32–34]).

A microstructure with a network interface can be developed using the existing technological methods to control the topology of exciton-polaritons in semiconductor Fabry–Perot microcavities with a high Q factor [35]. These methods are very physically diverse and are aimed at the modification of the common microcavity to obtain the required topological characteristics. Alternatively, an array of micropillars, which are microcavities with quantum dots and can be placed at nodes of the graph, as shown in Fig. 1. The considered artificial materials are of great interest for studying various phase transitions, as well as the Bose–Einstein condensation of exciton-polaritons, which can occur at high temperatures.

Finally, a different promising method to implement graphs shown in Fig. 1 involves fiber optic technologies, which allow the design of metanetworks for quantum communication and quantum Internet (see [36, 37]).

The interaction of the photon field with a system of TLSs within the waveguide graph structure shown in Fig. 1 is described by the Hamiltonian

$$\begin{gathered} H = \hbar \sum\limits_i^N \frac{{{{\omega }_{{0,i}}}\sigma _{i}^{z}}}{2} + \hbar {{\omega }_{{{\text{ph}}}}}\frac{1}{N}\sum\limits_i^N \sum\limits_v^{{{k}_{i}}} a_{v}^{\dag }{{a}_{v}} \\ + \;\frac{{\hbar g}}{{\sqrt N }}\sum\limits_i^N \sum\limits_v^{{{k}_{i}}} \left( {{{a}_{v}}\sigma _{i}^{ + } + a_{v}^{\dag }\sigma _{i}^{ - }} \right), \\ \end{gathered} $$
(1)

where \({{a}_{v}}(a_{v}^{\dag })\) is the annihilation (creation) operator of a photon of the mode of the vth waveguide, \(\sigma _{i}^{z}\) is the population inversion operator for the ith TLS, ω0,i is the resonance frequency of transition of the ith TLS from the ground to excited state, g is the coupling constant of TLSs to the photon field having the frequency ωph, and ℏ is the reduced Planck constant; for convenient further presentation, we accept ℏ = kB = 1, where kB is the Boltzmann constant. Hamiltonian (1) commutes with the operator of the number of excitations Nex, i of the ith node given by the expression

$${{N}_{{{\text{ex}},i}}} = \sum\limits_i^N \frac{{\sigma _{i}^{z}}}{2} + \sum\limits_v^{{{k}_{i}}} a_{v}^{\dag }{{a}_{v}}.$$
(2)

We use the mean field approximation within the thermodynamic grand canonical ensemble approach implying a nonzero chemical potential μ, which can be included by substituting ω0,i = Ω0,i + μ and ωph = Ωph + μ into Eq. (1) (see [38]). In addition, we assume that all photon modes are in coherent states \(\left| {{{\alpha }_{v}}} \right\rangle \) determined by the relation \({{a}_{v}}\left| {{{\alpha }_{v}}} \right\rangle = {{\alpha }_{v}}\left| {{{\alpha }_{v}}} \right\rangle \), where \({{\alpha }_{v}}\) is the same real parameter for all nodes. This approximation is justified if modes are strongly overlapped and have similar physical characteristics (cf. [22]). Averaging of Eq. (1) over coherent states \(\left| {{{\alpha }_{v}}} \right\rangle \) gives

$$H = \sum\limits_i^N \frac{{{{\Omega }_{{0,i}}}\sigma _{i}^{z}}}{2} + {{\Omega }_{{{\text{ph}}}}}\langle k\rangle {{\Lambda }^{2}} + \frac{{g\Lambda }}{{\sqrt N }}\sum\limits_i^N \left( {\sigma _{i}^{ + } + \sigma _{i}^{ - }} \right),$$
(3)

where \(\Lambda \equiv {{\alpha }_{v}} = \sqrt {{{N}_{{{\text{ph}}}}}} \) is the order parameter for Eq. (3) and Nph is the average number of photons in the network structure.

Further, we determine the density of excitations \(\rho \equiv \frac{1}{N}\langle \sum\nolimits_i^N {{{N}_{{{\text{ex}},i}}}} \rangle \), which is the normalized average total number of excitations and can be obtained from Eq. (2) in the form

$$\rho = \frac{{\langle k\rangle {{\Lambda }^{2}}}}{N} + \frac{1}{2}{{S}_{z}},$$
(4)

where \({{S}_{z}} = \frac{1}{N}\sum\nolimits_{i = 1}^N {\langle \sigma _{i}^{z}\rangle } \) is the average collective population inversion. In the mean field approximation, the partition function Z(N, T) = Tr(e–βH), where the Hamiltonian is given by Eq. (3), has the form

$$\begin{array}{*{20}{c}} {Z(N,T) = {{e}^{{ - \beta {{\Omega }_{{{\text{ph}}}}}\langle k\rangle {{\Lambda }^{2}}}}}} \\ { = \prod\limits_i^N 2\cosh \left[ {\frac{\beta }{2}\sqrt {\Omega _{{0,i}}^{2} + 4\frac{{{{g}^{2}}k_{i}^{2}}}{N}{{\Lambda }^{2}}} } \right],} \end{array}$$
(5)

where \(\beta \equiv 1{\text{/}}T\). Then, we suggest that the number of nodes is sufficiently large, \(N \gg 1\), and the structure of the network allows the transition to the continuous distribution \(p(k)\): \(\frac{1}{N}\sum\nolimits_i {...} \to \int_{{{k}_{{\min }}}}^{{{k}_{{\max }}}} {...} p(k)dk\), where \({{k}_{{\min }}}\) and \({{k}_{{\max }}}\) are the minimum and maximum degrees of the kth node (see [14]). In this case, using Eq. (5) and assuming that all TLSs are identical so that \({{\Omega }_{{0,i}}} = {{\Omega }_{0}}\), we obtain

$$\begin{array}{*{20}{l}} {{{\Omega }_{{{\text{ph}}}}} = \frac{{{{g}^{2}}}}{{\langle k\rangle }}\int\limits_{{{k}_{{\min }}}}^{{{k}_{{\max }}}} \frac{{{{k}^{2}}}}{\Gamma }\tanh \left[ {\frac{{\beta \Gamma }}{2}} \right]p(k)dk;} \end{array}$$
(6a)
$$\begin{array}{*{20}{l}} {\rho = \langle k\rangle \frac{{{{\Lambda }^{2}}}}{N} - \frac{1}{2}\int\limits_{{{k}_{{\min }}}}^{{{k}_{{\max }}}} \frac{{{{\Omega }_{0}}}}{\Gamma }\tanh \left[ {\frac{{\beta \Gamma }}{2}} \right]p(k)dk,} \end{array}$$
(6b)

where \(\Gamma \equiv \sqrt {\Omega _{0}^{2} + 4\frac{{{{k}^{2}}}}{N}{{g}^{2}}{{\Lambda }^{2}}} \) = \(\sqrt {\Omega _{0}^{2} + 4{{k}^{2}}g_{0}^{2}{{\Lambda }^{2}}} \).

The system of Eqs. (6a) and (6b) describes the main properties of the order parameter Λ appearing in Eq. (6a) as an implicit variable and the density of excitations ρ given by Eq. (6b) in the thermodynamically equilibrium state. To solve the system of Eqs. (6a) and (6b), it is also necessary to determine the chemical potential μ for various topologies of the network. To this end, we consider the networks with the power-law node degree distribution function [16]

$$p(k) = \frac{{(\gamma - 1)k_{{\min }}^{{\gamma - 1}}}}{{{{k}^{\gamma }}}},$$
(7)

where γ is the power-law exponent. The network with distribution function (7) satisfies the normalization condition \(\int_{{{k}_{{\max }}}}^{ + \infty } {p(k)} dk = \frac{1}{N}\), which means that the network with N nodes has more than one node with \(k > {{k}_{{\max }}}\). According to Eq. (7), \({{k}_{{\max }}} = {{k}_{{\min }}}{{N}^{{\frac{1}{{\gamma - 1}}}}}\).

The statistical properties of the network are described by the first, (\(\langle k\rangle \)), and second, (\(\langle {{k}^{2}}\rangle \), moments of the node degree distribution given by the expression (cf. [14])

$$\langle {{k}^{m}}\rangle = \int\limits_{{{k}_{{\min }}}}^{{{k}_{{\max }}}} {{k}^{m}}p(k)dk,\quad m = 1,2.$$
(8)

The parameter \(\zeta = \frac{{\langle {{k}^{2}}\rangle }}{{\langle k\rangle }}\) determines the main statistical properties of the considered network. The power-law exponent regions 1 < γ < 2, 2 < γ < 3, and γ > 3 correspond to anomalous, scale-free, and random regimes for \(\langle k\rangle \) and \(\zeta \), respectively. The properties of networks with distribution (7) at γ = 2 and 3 are calculated separately.

Figures 1a–1c show numerically simulated network structures referring to the (a) anomalous, (b) scale-free, and (c) random regimes. There are various algorithms of generation of such networks with the distribution close to Eq. (7) (see, e.g., [16]). Since the number of nodes in practice is always limited (N = 100 for Fig. 1), the numerically determined node degree distribution is discrete. It is represented by points in Fig. 1d that are the probabilities that the nodes of the networks in Figs. 1a–1c have the degrees corresponding to these probabilities. The dotted lines in Fig. 1d are approximations of these points by Eq. (7) with the power-law exponents γ = (red) 1.5, (green) 2.5, and (blue) 5 in the log–log scale.

The key feature of networks shown in Figs. 1a–1c is the presence of hubs, which are clearly seen as several points in the lower right corner of Fig. 1d. The largest hub has the degree \({{k}_{{\max }}}\). The network in the anomalous regime usually has the maximum number of hubs (see Fig. 1a). On the contrary, the network with the power-law node degree distribution in the random regime is close in characteristics to a network with the Poisson distribution for \(p(k)\). The number of hubs decreases with increasing γ; see the blue line in Fig. 1d.

Figure 2 shows the self-consistent numerical solutions of the system of Eqs. (6a) and (6b) for (a) the order parameter Λ and (b) the normalized chemical potential μ/g as functions of the density of excitations ρ for Δ/g = 0 and 9, where Δ = ωph – ω0 in the limit \(T \to 0\). The numerical estimates shown in Fig. 2 were obtained for cesium atoms as TLSs with the transition corresponding to the \({{D}_{2}}\) line at the frequency ω0/(2π) ≈ 352 THz [7, 20, 30]. The strong coupling of these atoms localized on the surface of solids to quantized radiation is currently achieved in experiments (cf. [29, 30]). The calculations were performed with g/(2π) = 1 GHz corresponding to microstructure containing N = 100 atoms shown in Fig. 1.

Fig. 2.
figure 2

(Color online) (a) Order parameter Λ and (b) normalized chemical potential μ/g versus the density of excitation ρ at the normalized detuning Δ/g = 9, ω0/g = 3.52 × 105, N = 100, kmin = 2, and T = 0 for γ = (brown) 1.5, (v-iolet) 1.7, (red) 2, (green) 2.5, and (blue) 4.5. The insets show the same curves for the resonance case with Δ = 0.

Full size image

As seen in Fig. 2а, the order parameter Λ increases with ρ at resonance Δ = 0.

The expression for the chemical potential in the limit of high temperatures \(\beta \to 0\) is easily obtained from Eqs. (6a) and (6b) in the form

$${{\mu }_{{1,2}}} = \frac{{{{\omega }_{{{\text{ph}}}}} + {{\omega }_{0}}}}{2} \pm \frac{1}{2}\sqrt {{{\Delta }^{2}} - 8{{g}^{2}}\zeta \left( {\rho - \frac{{\langle k\rangle }}{N}{{\Lambda }^{2}}} \right)} .$$
(9)

This expression is one of the main results of this work. It gives the upper (\({{\mu }_{1}}\)) and lower (\({{\mu }_{2}}\)) branches of excitations of coupled states of the quantized field and matter (cf. [39]) and makes it possible to determine the strong coupling condition.

At a low density of excitations, we can set \(\Lambda \to 0\), \({{S}_{z}} \simeq - 1\), which implies ρ ≈ –0.5; i.e., the ensemble of TLSs is inversionless. In this case, Eq. (9) describes two polariton branches, which can be obtained, e.g., with exciton-polaritons in semiconductor microcavities (cf. [13]).

At ρ = 0, the ensemble of TLSs is saturated when the numbers of particles on the lower and upper levels are the same, \({{S}_{z}} \simeq 0\).

At ρ > 0, population inversion occurs in TLSs and is maximal at ρ = 0.5 (\({{S}_{z}} = 1\)). It is remarkable that the ensemble of TLSs at a large detuning undergoes a structural transition to a different (parametric) type of excitations inherent in strong enhancement of radiation at ρ > 0.5 (see Fig. 2 and [38]).

The condition for this transition can be determined from Eq. (9) in the form \({\text{|}}\Delta {\text{|}} > 2g\sqrt \zeta \). The brown line in Fig. 2 does not satisfy this inequality, which corresponds to increasing ζ at γ = 1.5.

According to Eq. (9), the Rabi splitting frequency (the last term in Eq. (9)) increases significantly as a function of ζ in the anomalous regime of variation of the power-law exponent γ (see the inset of Fig. 1d). Thus, the collective coupling of TLSs to the quantized field can be strongly enhanced by choosing the appropriate power-law exponent γ, which determines the topology of the system shown in Fig. 1.

The phase transition to the superradiant state can be determined from Eqs. (6a) and (6b) with Λ = 0. The critical temperature of the phase transition Tc is quite simply represented for polaritons of the lower dispersion branch at Δ = 0 and has the form

$${{T}_{{\text{c}}}} = \frac{{\sqrt { - 8{{g}^{2}}\zeta \rho } }}{{4{{{\tanh }}^{{ - 1}}}(2\rho )}}.$$
(10)

This expression is another important result of this work. It is seen that the critical temperature of the superradiant phase transition Tc is proportional to \(\sqrt \zeta \); i.e., it is determined by the topology of the structure in Fig. 1. It is noteworthy that the phase transition temperature in the Ising model with the spin–spin coupling characterized by the distribution function (7) is finite and proportional to the parameter \(\zeta \) (see [14]).

As seen in Eq. (10), the critical temperature diverges Tc → ∞ at ρ → 0. This limit corresponds to the saturation of TLSs. According to Eq. (10), the critical temperature of the superradiant phase transition Tc can be very high even in the limit of a low density of excitations because of the statistical properties of the network itself, which are taken into account in Eq. (10) by means of the parameter ζ, which can be very large in the anomalous regime (see the inset of Fig. 1d).

Expression (10) for a given temperature T in the range of the density of excitations –0.5 < ρ < 0, i.e., for an inversionless TLS, gives the critical parameter

$${{\zeta }_{{\text{c}}}} = \frac{{2{{T}^{2}}{{{[\mathop {\tanh }\nolimits^{ - 1} (2\rho )]}}^{2}}}}{{{\text{|}}\rho {\text{|}}{{g}^{2}}}},$$
(11)

which determines the statistical properties of the network at the superradiant phase transition. In particular, the superradiant phase exists at ζ ≥ ζc. The behavior of the order parameter at large ζ values and high temperatures can be obtained from Eq. (6b) in the form

$$\Lambda \simeq \sqrt {\frac{{{{N}_{{\text{c}}}}{{x}_{{\text{c}}}}}}{{\langle {{k}_{{\text{c}}}}\rangle }}\left( {\frac{x}{{{{x}_{{\text{c}}}}}} - 1} \right)} ,$$
(12)

where \(x \equiv \frac{{\beta g}}{4}\sqrt {2\zeta {\text{|}}\rho {\text{|}}} \) is the parameter expressed in terms of the key parameters of the coupled system of the field and TLSs and xc is the value of this parameter at the phase transition point ζ = ζc. Expression (12) demonstrates that the number of superradiant photons vanishes at the phase transition point, which is characteristic of second order phase transitions.

Let us estimate the conditions for strong and ultrastrong coupling of TLSs to the quantized field for microstructures with the network architecture shown in Fig. 1. At a low density of excitations (such that \(\langle k\rangle {{\Lambda }^{2}}{\text{/}}N \ll 1\)), this condition can be obtained from Eq. (9) in the form

$$\Gamma ,\kappa \ll g\sqrt \zeta \lesssim {{\omega }_{{{\text{ph}}}}},$$
(13)

where Γ is the depolarization rate, κ characterizes possible losses of photons (cf. [1]), and the first and second inequalities are the strong and ultrastrong coupling conditions, respectively.

It seems not difficult to satisfy conditions (13) for microstructures with the network architecture shown in Fig. 1 because of the properties of node distribution (7) and the behavior of the parameter ζ (see the inset of Fig. 1d). In particular, it follows from Eq. (13) that the parameters of the network that satisfy, e.g., the criterion \(\zeta \simeq 0.01\omega _{{{\text{ph}}}}^{{\text{2}}}{\text{/}}{{g}^{2}}\) are sufficient to achieve the ultrastrong coupling (cf. [10]). Networks with the power-law node degree distribution in the anomalous regime have numerous various coupling channels between TLSs and the field, as well as numerous hubs, which can ensure the satisfaction of this criterion. In  this case, to estimate the achievability of the ultrastrong coupling, one can use the expression \(\zeta = {{k}_{{\min }}}\frac{{2 - \gamma }}{{3 - \gamma }}\frac{{{{N}^{{\frac{{3 - \gamma }}{{\gamma - 1}}}}} - 1}}{{{{N}^{{\frac{{2 - \gamma }}{{\gamma - 1}}}}} - 1}}\) obtained from Eqs. (7) and (8). The power-law exponent for atomic structures analyzed in Fig. 2 is \(\gamma = 1.219\) at \({{k}_{{\min }}} = 2\) and N = 100. For a microstructure with exciton-polaritons based on GaAs semiconductor quantum dots, the coupling constant to the quantized cavity field is \(g{\text{/}}2\pi = 1\) THz at the resonance wavelength \(\lambda = 767.3\) nm, which gives \(\gamma = 1.588\) at the same \({{k}_{{\min }}}\) and N values.

To summarize, a new concept of microstructures having the topology of a network (graph) with a power-law node degree distribution based on the cooperative coherent coupling of two-level systems, which are located at nodes of this network, to a quantized optical field has been proposed. It has been shown that the ultrastrong coupling regime can be achieved owing to features of the network architecture, which ensures the coupling of TLSs to the quantized field through numerous waveguide channels (edges of the graph) of the structure. The possibility of the giant enhancement of collective matter–field coupling by a factor of \(\sqrt \zeta \) has been predicted; this enhancement is ensured primarily in the anomalous region of the node degree distribution of the network structure. The superradiant phase transition, which occurs in the structure under consideration, has been considered. It has been shown that the phase transition temperature significantly depends on the parameter ζ, which determines the statistical properties (the first and second moments of the connectivity degree distribution) of the network structure. This critical temperature can be very high in the limit of a low d-ensity of excitations for the anomalous region of the network. The results obtained open qualitatively new prospects for quantum information processing by n-etwork and network-like systems, as well as for the observation and study of phase transitions involving polaritons in microstructures with the network co-upling topology at fairly high temperatures (cf. [36, 37]).