Negative Differential Resistance and Shapiro Steps in a Superconducting MoN Strip with a Cut

Regions with a negative differential resistance have been revealed in the voltage–current characteristics of superconducting MoN strips with a side cut under high-power microwave irradiation. A region with the negative differential resistance in the voltage–current characteristic is adjacent to steps, which are particularly pronounced at a low power of microwave radiation and are similar to Shapiro steps in the Josephson junction. The analysis within the time-dependent Ginzburg–Landau and heat conduction equations for the electron temperature has shown that the negative differential resistance is possibly due to the disordered (chaotic) motion of vortices across the strip near the cut, which occurs at a high microwave power.

1 INTRODUCTION

It is known that motion of vortices in superconductors can be phase locked by an alternating current, which appears, e.g., at the absorption of microwave electromagnetic radiation with the frequency ν. Phase locking occurs when the period of the alternating current T =1/ν is close to the characteristic time τ of vortex motion. This time is either the time of passage of the vortex across the superconductor τ = w/$v$ (here, w is the width of a superconducting bridge/strip or, e.g., the modulation period of superconductor thickness, and v is the average velocity of the vortex) or the time of passage between neighboring vortices τ = a/$v$ (here, a is the characteristic intervortex distance). Phase locking occurs as follows: at T ~ τ, the average velocity of vortices varies so that the time τ approaches the period of the alternating current T. As a result, the voltage $U \propto v$ is independent of direct current I; i.e., the voltage U does not change in a certain current range. This behavior is manifested as a step in a voltage–current characteristic [1–6] similar to Shapiro steps in Josephson junctions [7]. Phase locking in Josephson junctions occurs when the period T becomes equal to the period of 2π change in the phase difference of the superconducting order parameter in the junction.

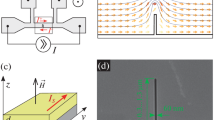
In this work, we study the effect of microwave radiation on the motion of vortices in the superconducting MoN strip with one side cut (see Fig. 1a). Current lines are concentrated near the edge of the cut (see Fig. 1b), which results in a locally stronger suppression of the superconductivity and determines the place of nucleation of vortices (entry point of vortices) when the transport current I exceeds the critical value I_c. Thus, it is possible to implement a regime where vortices enter the superconductor through a certain controlled place in a quite wide current range (other entry points of vortices can appear at I ≫ I_c). The number of vortices simultaneously moving in the strip can be small (down to one) and depends on the current and width of the strip. A similar problem of the superconducting strip with two cuts opposite to each other was theoretically considered by Aslamazov and Larkin in [8], where they calculated the characteristics of a resistive state similar to Josephson junctions, including Shapiro steps, and predicted the appearance of “kinks” in voltage–current characteristics under the variation of the number of moving vortices.

Fig. 1.

(Color online) (a) Layout for measurements of a superconducting bar with cut. (b) Current density distribution in the cut region. (c) Layout of microwave excitation. (d) Electron microscopy image of the strip with cut.

In this experiment, we measured the voltage–current characteristic similar to the voltage–current characteristic of an overdamped Josephson junction in the current range I_c < I < I* (here, I* is the switching current to the normal state) and Shapiro steps, but we did not observe kinks. However, our main result is the detection of the negative differential resistance (NDR) in voltage–current characteristics, which appears at a high microwave power. The calculations with the time-dependent Ginzburg–Landau and heat conduction equations for the electron temperature showed that the system under study allows a chaotic motion of vortices and calculated voltage–current characteristics have an NDR region. This makes it possible to relate our result to the NDR observed for the underdamped Josephson junction. It is known that a chaotic regime, i.e., the absence of any time-periodic change in the phase of the superconducting order parameter and the voltage in the Josephson junction, can occur in a certain range of the parameters at a s-ufficiently high microwave power [9–11]. When approaching this regime, voltage–current characteristics of Josephson junctions can contain regions with NDR [9–11] or even with a negative resistance [11, 12]. Compared to the underdamped Josephson junction, the main “inertial” parameters in the MoN strip with the cut are the finite relaxation time of electrons ${{\tau }_{E}}$ to the equilibrium state and the time of variation of the superconducting order parameter. It is noteworthy that, in contrast to Josephson junctions, the existence of these times does not lead to the hysteresis of v-oltage–current characteristics in the current range I_c < I < I* at low voltages, where Shapiro steps are observed and the NDR regime occurs. Hysteresis in our system appears when the current exceeds the value I* and strong electron heating transfers the superconducting strip to the normal state; the strip returns to the superconducting state at a much lower current I < I_r ≪ I_c.

2 SUPERCONDUCTOR–NORMAL METAL STRUCTURES

In this work, we study the electron transport under microwave irradiation in a series of strips with a width of $w = 2.5$ μm and a length of L = 30 μm fabricated from thin superconducting MoN films. The films were grown on 10 × 10-mm standard Si substrate plates without removal of the oxide layer using the magnetron deposition technique in a base vacuum of about 1.5 × 10^–7 mbar. The MoN film was formed by magnetron deposition of molybdenum in the 10 : 1 mixture of Ar : N₂ gases at a pressure of 10^–3 mbar and at room temperature. The layer thickness d_S = 20 nm was measured by X-ray diffractometry. The layer was coated with a 5-nm protective Si film. The resistivity at a temperature of 10 K was ρ ≈ 150 μΩ cm, the resistance per square was R_□ = 75 Ω, and the critical superconducting transition temperature was 7.8 K.

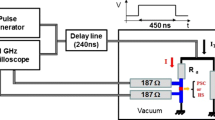
Transport measurements were performed by the standard four-terminal method in a given dc regime in a helium storage dewar with the complete immersion of the sample in liquid helium (temperature 4.2 K) at atmospheric pressure. A niobium screen protected the sample from the external magnetic field. A two-cascade analog RC filter with a passband of 5 kHz operating at room temperature was used to suppress high-frequency noise in leads. The microwave field was generated by a whip antenna (Fig. 1c) without special matching of impedances.

The 60-nm-wide cut at the edge of the strip was formed by a focused gallium ion beam. Strips in the series differ in the cut with lengths of 300, 900, and 1300 nm (the electron microscopy image of one of the strips is shown in Fig. 1d). An increase in the length of the cut from 300 to 1300 nm reduces the critical current I_c0 in the absence of irradiation from 1.00 to 0.49 mA (the critical current for the strip without cut is I_c0 = 1.8 mA).

The voltage–current characteristic of the sample with the cut has no hysteresis in the current range I_c < I < I* (the sample without cut above the critical current was transferred stepwise to the normal state). Microwave irradiation leads to a decrease in the critical current and to the shift of voltage–current characteristics, as shown in the inset of Fig. 2. This effect is due both to the direct summation of the direct and induced high-frequency currents and to the heating of the sample by microwave radiation absorbed by normal electrons. The voltage response $U(\nu )$ at the current I_m as a function of the microwave frequency ν has an obvious resonance character (see Fig. 2). The spectrum of the response corresponds to the geometry of the sample on a holder and changes at the assembly of the sample. The measurements were carried out at frequencies of maxima in the spectrum.

Fig. 2.

(Color online) Typical microwave frequency response spectrum $U(\nu )$ at a given measuring current I_m < I_c0, where I_c0 is the critical current in the absence of irradiation. The inset shows the voltage–current characteristics of the sample in the absence and presence of microwave irradiation.

3 RESULTS

Figure 3 shows voltage–current characteristics of the sample with 1300-nm-long cut both in the absence of microwave irradiation (lines with the maximum critical current in Figs. 3a–3c) and under microwave irradiation. A finite voltage is due to the motion of vortices, which enter the strip near the edge of the cut at the current above the critical value and move across the strip. The velocity and number of vortices increase with the current (this is qualitatively confirmed by the numerical calculation presented below), which leads to an increase in the voltage. The transition of the sample to the normal state at I > I* has a stochastic (random) character. The spread of quench currents at the same nominal radiation power was no more than ~0.01 mA.

Fig. 3.

(Color online) Experimental voltage–current characteristics of the sample with the 1300-nm-long cut versus the microwave power for frequencies of (a, d) 400, (b, e) 1000, and (c, f) 2600 MHz; I_c0 = 0.48 mA is the critical current of the strip in the absence of microwave irradiation. With increasing microwave power, the voltage–current characteristics are shifted to the left. The NDR region is presented in panels (d–f) on a magnified scale.

Steps at voltages $U = nh\nu {\kern 1pt} /{\kern 1pt} 2{\text{|}}e{\text{|}}$, where n is an integer, h is the Planck constant, and e is the charge of the electron, appear under microwave irradiation in voltage–current characteristics (they are marked by horizontal lines in Fig. 3). With increasing radiation power, the width of the steps varies nonmonotonically, qualitatively similar to Shapiro steps for Josephson junctions.

Negative differential resistance (NDR) appears in voltage–current characteristics $U(I)$ at a high irradiation power. This effect was detected in all three strips under study with different cut lengths. The NDR region was observed in the frequency range of 0.3–3 GHz. With increasing temperature, the nonmonotonicity of $U(I)$ was weakened and the effect disappears (at 5.5 K). Voltage–current characteristics with the NDR region at different frequencies are quantitatively different (see Fig. 3), but the effect itself is qualitatively present.

Such N-shaped voltage–current characteristic is rather rare in superconductors. The NDR usually appears in an S-shaped voltage–current characteristic, which can be observed in a given voltage regime (see, e.g., review [13]). In our case, a regime of given current occurs. We know only of a few superconducting systems whose voltage–current characteristics exhibit the NDR region of this type. The first system is an underdamped Josephson junction under microwave irradiation, where the NDR region appears at the chaotic dynamics of the superconducting phase difference in the junction [9–11]. The second system is a superconducting film with a periodic array of artificial pinning centers in a magnetic field slightly stronger than the so-called first matching field at which one vortex can be located at each pinning center [14–16]. Negative differential resistance appears in such a perforated film in the absence of microwave irradiation because of a complex collective dynamics of a large ensemble of vortices and depends on the prehistory; i.e., voltage–current characteristics are hysteretic even without dissipation [14]. The NDR region appears in this system when the motion of vortices is disordered. The third system is a perforated Nb strip [17], where an asymmetric pinning profile of vortices is specially cr-eated to ensure the diode effect in a nonzero magnetic field. The NDR appears in this system under microwave irradiation in the magnetic field when vo-ltage–current characteristics become asymmetric ($U(I) \ne - U( - I)$). However, this effect was not studied in detail and it is unclear whether it is due to the disordered motion of vortices. In the context of studied Josephson junctions, which are very close in physical properties to our system, we assume that the NDR in our case can be due to the chaotic dynamics of vortices. To test this assumption, we numerically simulate the dynamics of vortices in the superconducting strip with a single cut.

4 NUMERICAL EXPERIMENTS

The numerical calculations were performed with the time-dependent Gunzburg–Landau equation [18] for the superconducting order parameter Δ = ${\text{|}}\Delta {\text{|}}\exp (i\phi )$

$$\begin{gathered} \frac{{\pi \hbar }}{{8{{k}_{{\text{B}}}}{{T}_{{\text{c}}}}}}\left( {\frac{\partial }{{\partial t}} + \frac{{2ie\varphi }}{\hbar }} \right)\Delta = \frac{\pi }{8}\xi _{{\text{c}}}^{2}{{\left( {\nabla - i\frac{{2e}}{{\hbar c}}A} \right)}^{2}}{\kern 1pt} \Delta \\ + \;\left( {1 - \frac{{{{T}_{e}}}}{{{{T}_{{\text{c}}}}}} - \frac{{{\text{|}}\Delta {{{\text{|}}}^{2}}}}{{\Delta _{{{\text{GL}}}}^{2}}}} \right)\Delta . \\ \end{gathered} $$

(1)

Here, the Joule heating of electrons is taken into account through the electron temperature T_e, which is determined from the heat conduction equation

$$\frac{{\partial {{T}_{e}}}}{{\partial t}} + D{{\nabla }^{2}}{{T}_{e}} - \frac{1}{{{{\tau }_{E}}}}\left( {{{T}_{e}} - {{T}_{0}}} \right) + \overline j {\kern 1pt} \overline E {\text{/}}{{C}_{v}} = 0.$$

(2)

To take into account the current flow continuity, we solved the equation for the electric potential φ,

$${\text{div}}{\kern 1pt} j = {\text{div}}{\kern 1pt} ({{j}_{s}} + {{j}_{n}}) = {\text{div}}\left( {\frac{{{{\sigma }_{n}}}}{e}\frac{{\pi {\text{|}}\Delta {{{\text{|}}}^{2}}{{q}_{s}}}}{{4{{k}_{{\text{B}}}}{{T}_{{\text{c}}}}}} - {{\sigma }_{n}}\nabla \varphi } \right) = 0.$$

(3)

In Eqs. (1)–(3), T_c is the superconducting transition temperature, D is the diffusion coefficient, ${{\sigma }_{n}} = 2{{e}^{2}}D{{N}_{0}}$ is the conductivity, N₀ is the electron density of states on the Fermi surface per electron spin, ${{q}_{s}} = (\nabla \phi - 2eA{\text{/}}\hbar c)$, ${{\tau }_{E}}$ is the relaxation time of the nonequilibrium temperature, ${{C}_{v}} = 2{{\pi }^{2}}k_{B}^{2}N(0){{T}_{0}}{\text{/}}3$ is the electronic specific heat, $\xi _{c}^{2} = \hbar D{\text{/}}{{k}_{{\text{B}}}}{{T}_{{\text{c}}}}$, and Δ_GL = 3.0k_BT_c.

Equations (1)–(3) are valid when the inelastic electron–electron scattering time is small, which ensures rapid thermalization in the electron subsystem and the establishment of the electron temperature ${{T}_{e}}(x,y,t)$ different from the phonon temperature T_p and substrate temperature ${{T}_{0}}$ (we assume that ${{T}_{{\text{p}}}} = {{T}_{0}}$ and ${{T}_{e}} - {{T}_{0}} \ll {{T}_{0}}$). Furthermore, we use for simplicity the expressions for the specific heat and thermal conductivity of electrons in the normal state. This model was chosen in order to at least qualitatively explain the experiment. For this reason, the simplest model was used to take into account the heating of electrons and the characteristic time of their cooling ${{\tau }_{E}}$ in Eq. (2). The real situation can be more complex, e.g., as discussed in [19–21]. The superconductor–insulator boundary conditions $\partial {{T}_{e}}{\text{/}}\partial n = 0$, $\partial {\text{|}}\Delta {\text{|/}}\partial n = 0$, and ${{\overline j }_{s}}{{{\text{|}}}_{n}} = {{\overline j }_{n}}{{{\text{|}}}_{n}} = 0$were imposed at the edge of the cut and on the side surfaces of the superconducting strip, whereas the superconductor–normal metal boundary conditions ${\text{|}}\Delta {\text{|}} = 0$ and $- {{\sigma }_{n}}\nabla \varphi = I{\text{/}}wd$ were imposed at the ends of the strip, which makes it possible to “inject” the current $I = jwd$ into the strip (we set ${{T}_{e}} = {{T}_{0}}$ at the ends of the strip). The calculations were performed with the width of the superconductor w = 200ξ_c, which is approximately half the experimental value (for MoN, D = 0.4 cm²/s [22] and ξ_c ≈ 6.2 nm at T_c = 7.8 K). This choice allows us to reduce the computation time and to ensure the existence of more than one vortex in the superconductor in the resistive state, which is expected in the experiment. The length $L = w$ makes it possible to minimize the effect of current contacts on the supercurrent distribution near the cut (its length and width were chosen as 𝓁 = 50ξ_c and 2ξ_c, respectively) and to reduce the computation time. In the numerical calculations, the time, distance, temperature, current, voltage, and Δ were taken in units of τ_c = ℏ/(k_BT_c), ξ_c, T_c, Ginzburg–Landau depairing current I_dep [18], U₀ = k_BT_c/|e|, and k_BT_c, respectively.

The supercurrent in the calculations had the direct, I_dc, and alternating, I_accos(2πt/T), components. For each direct current value, we obtained the dependence $U(t)$ during 2000τ_c = 20T for I_ac ≤ 0.2I_dep or during 4000τ_c = 20T for I_ac ≥ 0.4I_dep (the calculations were performed with the period T = 100τ_c, τ_E = 30τ_c, and T₀ = 0.8T_c). The voltage was then averaged in time; the time-averaged voltage is shown in Fig. 4 as a function of the direct current for various alternating current amplitudes I_ac.

Fig. 4.

(Color online) Theoretical voltage–current characteristics of the superconductor with the cut at various amplitudes of the alternating current. Numbers mark the corresponding Shapiro steps in voltage–current characteristics at I_ac/I_dep = 0.1. The inset shows the voltage–current characteristic in a magnified scale at I_ac/I_dep = 0.43.

In the current range I_c < I_dc < I*, the calculated voltage–current characteristics do not demonstrate hysteresis (at least, in a current step of 0.02–0.05I_dep). The superconductor is transferred to the normal state at I_dc > I* and returns to the superconducting state at I_r ≪ I_c. The current I_r depends on ${{\tau }_{E}}$: I_r decreases with increasing ${{\tau }_{E}}$. The resistive state in this model is due to the production of vortices near the edge of the cut and their motion to the opposite end of the superconductor when I_dc > I_c. The velocity and number of the vortices increase with the current. In particular, five vortices move behind each other in the strip when I_ac = 0 and I_dc ~ I*, whereas only one moving vortex is present in the superconductor at I_dc ~ I_c.

The alternating current with the amplitude I_ac reduces the critical current and leads to the appearance of steps in voltage–current characteristics at voltages $U = nh\nu {\text{/}}2m{\text{|}}e{\text{|}}$, where m and n are integers. The steps appear when the time of motion of vortices across the superconductor becomes multiple of the alternating current period. This effect for a similar system was previously predicted in [8] and the origin of these steps is similar to that of Shapiro steps in Josephson junctions. At a large amplitude of the alternating current, regions with a nonmonotonic dependence U(I_dc) appear in voltage–current characteristics. This regime is characterized by the chaotic motion of vortices, in contrast to the periodic motion at small amplitudes I_ac.

This is demonstrated in Fig. 5, where the time dependence of the |Δ| near the edge of the strip opposite to the edge with the cut (point A in Fig. 1b) is shown. When |Δ|_A = 0, the vortex passes through point A and leaves the superconductor. At I_ac = 0.1I_dep and low I_dc, several periods T are required for the vortex to pass across the strip (see Fig. 5a). During this time, the vortex enters and leaves the superconductor at the edge of the cut and passes farther from the cut in each next period, as seen in the dynamics of |Δ|_A(t), which reflects the motion of the vortex toward (|Δ|_A decreases) and away from (|Δ|_A increases) point A. The discovered effect is due to the appearance of the trace behind the passed vortex, which is a region with suppressed superconductivity and locally increased temperature T_e. After the complete passage of one vortex across the superconductor, the process repeats periodically. The velocity of the vortex and the number of vortices in the superconductor increase with I_dc, but the motion of vortices remains periodic in time.

Fig. 5.

(Color online) Time dependence of the magnitude of the superconducting order parameter at point A in Fig. 1b at various I_ac and I_dc values. For convenient presentation, we chose the minimum value |Δ|_A/(k_BT_c), which means that the vortex passes across the superconductor.

At a large amplitude I_ac, the picture is different (see Fig. 5b). The variation of |Δ|_A is not periodic, which means the aperiodic motion of vortices. In this regime, the nonmonotonic dependence U(I_dc) appears (see the inset of Fig. 4), similar to the nonmonotonic dependence U(I_dc) that can arise under microwave irradiation in underdamped Josephson junctions characterized by “inertia” caused by the capacitance of the junction [9–11]. Our system also has inertia, as clearly seen in the dynamics of |Δ|_A at small amplitudes I_ac (see Fig. 5a), which is due to a finite variation time of the magnitude of the superconducting order parameter and a finite relaxation time of nonequilibrium electrons ${{\tau }_{E}}$.

We note that there are quantitative differences between the experiment and theory. The experimental voltage–current characteristic does not demonstrate a jump in the voltage at I_dc = I_c; it exhibits only integer Shapiro steps, which are less pronounced than in the theoretical voltage–current characteristic. The experimental and theoretical characteristics of the NDR are also quantitatively different. We believe that these differences are mainly due to noise in the experiment. Indeed, in the absence of filters, Shapiro steps become almost invisible in voltage–current characteristics (they can be identified only by analyzing the differential resistance), I_c and I* become lower, and the voltage range with the vortex branch in voltage–current characteristics is reduced. Our filters possible incompletely remove external noise in the system. Furthermore, there is internal noise caused by thermal fluctuations. The stochastic character of the switching of the superconductor to the normal state when approaching I* and the presence of the “tail” in voltage–current characteristics near the critical current even in the presence of filters indicate the effect of internal and possibly external noise. This noise can smooth features in voltage–current characteristics (voltage jump and steps).

Our calculations show that the NDR does not disappear at doubling/halving the frequency (at a chosen ${{\tau }_{E}}$ value) and at doubling/halving ${{\tau }_{E}}$ (at a chosen frequency). However, the dependence of the NDR parameters on the frequency of the alternating current and on ${{\tau }_{E}}$ was not analyzed in more detail because the quantitative comparison of the theory and experiment is hardly possible because we used a simplified theoretical model.

5 CONCLUSIONS

We have revealed that regions with a negative differential resistance appear in the voltage–current characteristics of superconducting MoN strips with a side cut under high-power microwave irradiation. The calculations within the time-dependent Ginzburg–Landau and heat conduction equations for the electron temperature have shown that a similar effect occurs in theoretical voltage–current characteristics in the chaotic regime of motion vortices crossing the superconducting strip near the cut. The proposed explanation of the discovered effect is similar to the reason for the appearance of the negative differential resistance in Josephson junctions with a low viscosity.