The discovery of layer-by-layer thinning transitions in freely suspended smectic nanofilms is one of the most striking discoveries in the physics of liquid crystals in last several decades [1–8]. Smectic liquid crystals have the one-dimensional ordering of molecular layers. An important physical feature of smectic ordering is, in particular, that the heated bulk sample begins to melt with inner layers rather than with the surface, as in most crystals. This occurs because the amplitude of smectic fluctuations is large and because these fluctuations are “frozen” near the surface. The translational order parameter of surface layers is larger than that in the bulk. This leads to a nontrivial behavior of freely suspended thin films two surfaces of which are adjacent to air. The order parameter of the heated inner layers becomes so small that these layers are melted. As a result, the film becomes structurally unstable. The existing theoretical description of this phenomenon implies that the pressure difference between air and the film \(\Delta P = {{P}_{{{\text{air}}}}} - {{P}_{{{\text{film}}}}}\) and its dependence on the thickness of films result in the extrusion of the inner “melted” layer of the film. The material of this layer escapes to the meniscus and the thickness of the film decreases. Surface ordering in the remaining thinner film holds its length upon thinning and leads to the stability of inner layers of the film. The subsequent heating induces new thinning transitions. A stepwise decrease in the thickness of the film at thinning transitions was observed in various smectic phases: in the nonpolar smectic-A phase (Sm A) with the orthogonal orientation of long axes of molecules in layers [1–6] and in the ferroelectric smectic-C* phase (Sm C*) [7]. Performed numerical and analytical calculations [5, 8–15], in particular, those based of the de Gennes theory of presmectic films [16, 17], confirmed the structural instability of films at a high temperature and the possibility of escaping this instability through layer-by-layer thinning transitions.

Some circumstances are significant for thinning transitions. Below the temperature of the bulk phase transition, numerous dislocations form a meniscus of the freely suspended film; above the bulk transition temperature, the smectic film contacts the meniscus formed by the phase without layer ordering and dislocation. The main attention in previous experimental and theoretical studies was paid to the temperature dependence of the thinning transition. To study the dynamics of these transitions, the authors of [18] measured the velocity of the thinning front (edge dislocation) between films with two thicknesses at a temperature below the temperature of the bulk phase transition TC, i.e., below the temperature of the absolute instability of films. Thinning was induced by the local heating of a small region of the film. The dynamics of transformation of islands and holes (regions of larger and smaller thicknesses than the film thickness) was studied in the subsequent works [19–22]; in particular, unique measurements were performed with single-molecular-layer holes [21]. Investigations were made at T < TC. Spontaneous transitions were also observed above TC [19]. The authors of [4] observed an increase in the velocity of the thinning front with increasing temperature above the temperature of the Sm A–isotropic liquid bulk phase transition in thin films with a thickness of 3–5 layers. Transitions were also induced by the local heating of a small region of the film.

Layer thinning transitions with reproducible transition temperatures were experimentally observed in some materials. At the same time, smectic nanofilms of numerous materials are not melted above the temperature of the bulk melting phase transition, but both layer-by-layer thinning and transitions with a decrease in the thickness of the film by several smectic layers are observed and temperatures of thinning and destruction of films are not reproduced. Thinning and destruction of films of these materials can occur at various temperatures above TC. Since the phenomenon of thinning of nanofilms is striking and the formation of various nanostructures is of general interest [23–26], thinning transitions have been intensively studied in the last decades. However, a number of questions, primarily concerning the initial stage of formation of a thin film from a thicker one, are still unanswered.

In this work, we discover a mechanism of thinning of nanofilms that has not been observed in experiments and has not been predicted theoretically. Studies were performed in the region of the structural instability of 12CB cyanobiphenyl nanofilms (Synthon Chemicals). The Sm A–isotropic liquid bulk phase transition in the bulk sample occurs at 58°C. A significant change in the shape of the meniscus near the thinning transition, the formation of a thinner region in it near the boundary with the film, and the growth of this region were observed, which results in the thinning of the entire film.

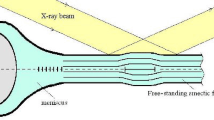
Optical measurements were performed with an Olympus BX51 that operated in reflected light and was connected to an AvaSpec-2048L spectrometer (Avantes) and a Baumer VCXU-02C high-speed video camera with a recording speed up to 600 fps. This equipment made it possible to simultaneously detect a change in the number of layers in a nanofilm and the dynamics of thinning transitions. Thermostatic devices allowing optical measurements were used. Films were prepared in the smectic phase in a circular hole with a diameter of 4 mm in a thin glass plate. Prepared films usually contain regions with nonuniform thicknesses. Before the beginning of the experiment, films were kept at a constant temperature for several tens of minutes to reach a uniform thickness.

To study the behavior of films near instability points, it is important to know the number of layers N in the nanofilm before and after each thinning transition. Thinning transitions were detected by the intensity of light reflected from them and by the transition front passing through the film (motion of the edge dislocation separating films with two different thicknesses leads to a decrease in the thickness of the film). The intensity of light reflected back from nanofilms with a thickness less than nine molecular layers is proportional with a high accuracy to the square of the number of layers \(I(N) \sim {{[N\pi d({{n}^{2}} - 1){\text{/}}\lambda ]}^{2}}\) [27], where d is the thickness of the smectic layer and n is the refractive index. The thickness (number of layers) of thicker films can be determined using a more complex dependence I(N) [27].

Circles in Fig. 1 mark the maximum temperatures to which films with different numbers of layers N were successfully heated. Thinning and destruction transitions in films could also occur at lower temperatures. It can be assumed that circles are near temperatures of absolute instability of films with a given number of l-ayers N. This assumption is confirmed by results reported below on the shape of the meniscus and the process of formation of thinner films. The formation of droplets of high-temperature phase without layer ordering, as well as point and linear defects, is possible near instability temperatures above the temperature of the bulk phase transition [23, 28–30]. The formation of droplets and defects in films was not observed in the series of thinning transitions presented in this work.

Fig. 1.
figure 1

(Color online) Thickness of the smectic film me-asured in the number of smectic layers N versus the temperature above the temperature TC of the bulk phase transition to the isotropic liquid. The line is the approximation of experimental data by the function N = \({{N}_{0}}{{[({{T}_{N}} - T\text{*}){\text{/}}T\text{*}]}^{{ - \nu }}}\), where \(\nu = 0.61\).

Full size image

According to the de Gennes theory of presmectic films, the temperatures of the structural instability of films TN are related to the number of layers N as \(N = {{N}_{0}}{{[({{T}_{N}} - T\text{*}){\text{/}}T\text{*}]}^{{ - \nu }}}\), where the critical temperature T* is close to the phase transition temperature TC to the structure without layer ordering and ν is the critical exponent. The fitting of the dependence \(N = {{N}_{0}}{{[({{T}_{N}} - T\text{*}){\text{/}}T\text{*}]}^{{ - \nu }}}\) to the experimental data presented in Fig. 1 gives \(\nu \approx 0.6\), which is close to the values previously obtained [5, 31]. Theoretical and experimental studies were focused on the instability of smectic nanofilms themselves. As in previous works, the role of the meniscus both below and above TC was usually reduced to the inducing of the Laplace pressure γ/R due to the curvature of the meniscus 1/R. At the same time, the meniscus in which the phase transition occurs at TC is responsible for the existence of films themselves. The complex profile of the meniscus at a low temperature T < TC is formed by smectic layers (Fig. 2a) with a large number of dislocations with the giant Burgers vector. The bulk smectic sample above TC is melted. An interface is formed between the smectic film and the meniscus in the phase without layer ordering (Fig. 2b). Such an interface can in turn be considered as an additional meniscus limiting the smectic film. Despite numerous experimental and theoretical studies of the layer-by-layer thinning, this heating-induced change in the shape of the meniscus was considered only in [31].

Fig. 2.
figure 2

(Color online) (a) Schematic of the nanofilm with the smectic meniscus at a temperature below the temperature TC of the bulk phase transition. (b) At T > TC, an interface (meniscus) is formed, separating the smectic film and the isotropic phase with layer ordering only near the interface with air.

Full size image

In this work, we focus on the transformation of the meniscus because the large curvature of the interface between phases at the first order smectic–isotropic liquid phase transition can significantly affect the dynamics of thinning. The boundary between the smectic film and meniscus with the curvature 1/rN, where rN = Nd/2, results in the Laplace pressure ΔPN = 2γ1/(Nd), where γ1 is the surface tension at the interface. Taking γ1 ≈ 10–5 N/m [32], we obtain ΔPN ~ 600 Pa for the film with a thickness of 10 layers. This pressure is noticeably higher than the excess pressure of 7–40 Pa produced by the meniscus of the film between smectic and air [5] at T < TC or between the liquid and air at T > TC. Above, the presence of the surface smectic layer in the isotropic meniscus was not taken into account; the thickness of this layer (the correlation length of surface ordering) changes with the temperature and can lead to the smooth increase in ΔP between thinning transitions. To completely understand the dynamics of layer-by-layer thinning, the further development of the theory of presmectic nanofilms is required, including (i) the study of the shape of the nanointerface between the smectic film and the phase without layer ordering, (ii) the pressure produced by this interface, and (iii) the inclusion of percolation effects and the nonequilibrium dynamics of dislocations.

We studied changes in the shape of the meniscus near thinning transitions (Fig. 3). Under the heating above the temperature of the bulk melting phase transition, the edge of the meniscus is displaced toward the center of the film and the front of the meniscus is transformed (Figs. 3a, 3b). The most drastic transformation of the meniscus was observed near the thinning transition. After the smooth variation of the position and shape of the meniscus (Figs. 3a, 3b), immediately before the thinning transition, the thin part of the meniscus penetrates deeper into the nanofilm (Figs. 3c, 3d), forming a layer with a thickness of about and smaller than 50 nm. Thicker droplets are also nucleated in this part of the meniscus (dark and light circular inclusions, Figs. 3c, 3d). The thickness of the meniscus near the meniscus–smectic film interface decreases upon relaxation (Fig. 3d). The continuous variation of the thickness of the meniscus (the meniscus is darker near the boundary with the film (Fig. 3d) indicates the absence of the layer (discrete) structure at least in the middle of the meniscus. It is noteworthy that the boundary between the meniscus and the film exists even when the thickness of the meniscus becomes smaller than the thickness of the film (the front of the meniscus is darker than the film, Fig. 3d), which indicates the significant difference between their structure. The absence of layer ordering in the meniscus and the possibility of the smooth variation of its thickness can lead to large fluctuations of the thickness. If the thickness of the meniscus becomes locally smaller than the thickness of the film, the state with the smectic ordering of layers becomes energetically favorable. The formation of a thin region with a smaller number of smectic layers than in the film was observed in the experiment (the dark region in the thin part of the meniscus in Fig. 3e). We emphasize that the state with layer ordering and with a smaller number of layers than in the initial film is formed in the meniscus and then propagates over the entire film (Fig. 3f). The thinning transition occurs in the entire film; the meniscus itself decreases in size (Fig. 3f).

Fig. 3.
figure 3

(a–d) Smectic film with N = 9 near the meniscus before the thinning transition. (a) Film at T = 59.5°C far from the thinning temperature. (b) Heating-induced transformation of the shape of the meniscus near the contact with the smectic film at T = 60.15°C. (c) Formation of a wide flat region of the meniscus at T = 60.26°C. (d) Meniscus with smooth variation of the thickness (intensity of reflection decreases when approaching the film) at T = 60.29°C. (e) Formation of a thin region in the meniscus (dark region) leads to the thinning of the film at T = 60.31°C. (f) Meniscus and a thinner film at T = 60.34°C immediately after the thinning transition.

Full size image

Our studies have revealed new features of thinning transitions in freely suspended smectic nanofilms. We have proposed a mechanism of thinning of nanofilms that has not been observed in experiments and has not been predicted theoretically. The size and shape of a meniscus change near the thinning transition. The longitudinal size of the meniscus increases significantly. The front of the meniscus penetrates deeper into a nanofilm and the thickness of the meniscus in its thin region becomes about and smaller than the thickness of the nanofilm. The thinner film is formed in the meniscus near its edge and propagates over the entire film. The transformation of the meniscus induces the thinning of the film.

The instability of the meniscus described above is the main new result of this work. It was previously believed that the thinning of smectic nanofilms above TC is caused by the instability of layer ordering in films. We have shown that not only the film but also the meniscus becomes unstable above TC. Which of these instabilities occurs earlier can in particular depend on material parameters, on the probability of nucleation of the thin film, and on the prehistory. We have detected the instability of the meniscus and have experimentally demonstrated that this instability can induce the thinning of the nanofilm. The results obtained have indicated that processes of thinning of smectic films are much more complex and richer than was previously believed. The understanding of these processes is currently far from being complete and further experimental and theoretical studies are required.