1 INTRODUCTION

The structure and properties of vortex-like inhomogeneities (magnetic vortices, skyrmions, bimerons, etc.) arising in certain classes of magnets are currently under active investigation, stimulated by actual prospects for their use in various spintronic devices, as well as in the new generation magnetic memory devices [1]. Such interest in them is also due to their topological protection, nanoscale, high mobility, and other unique spin–electron characteristics [2–4]. In this work, we extend the ideas outlined in [5] in application to the simplest one-dimensional model and propose another type of vortex-like inhomogeneities formed in thin magnetic films with artificially created holes (antidots [6]) or nonmagnetic inclusions.

2 CONTINUOUS MODEL

We consider a thin ferromagnetic film with strong easy plane uniaxial anisotropy and one hole. Such anisotropy implies that the magnetization vector almost does not leave the plane of the film. Then, the energy of the magnetic film can be approximately represented in the form [5]

$$E = \int A{{(\nabla \theta )}^{2}}hdS,$$
(1)

where angle θ specifies the orientation of the in-plane magnetization vector, A is the exchange integral, and h is the film thickness. Here, we assume that the demagnetizing fields in the material under study are much lower than the exchange field.

In the case of a film without topological features, functional (1) has a single minimum E = 0, which takes place at θ = const and corresponds to the uniform distribution of magnetization. However, if there is only one hole in the film (the feasibility of such nanoscale perforations in practice is confirmed by similar experiments with graphene [7]), this statement becomes incorrect. Let us introduce a polar coordinate system \((r,\varphi )\) in the plane and assume that the magnetic material fills the region Rin ≤ r ≤ Rex, thus having the shape of a perforated disk. In this case, in addition to the homogeneous state, there will also appear local minima, which are nontrivial solutions of the Euler–Lagrange equation for functional (1), namely, the Laplace equation Δθ = 0. The point is that, with the specified sample topology, the angle θ may no longer be a single-valued function of the radius vector. Instead, it suffices to satisfy the physically equivalent condition θ(r, φ + 2π) = θ(r, φ) + 2πk, where k is an integer. It is easy to see that, for a given value of k, which in this case has the meaning of a topological charge, θ(r, φ) = kφ + const is a solution of the equation Δθ = 0. Note that the solutions corresponding to different values of k are topologically nonequivalent, and the transitions of the magnetic material between the corresponding states would be associated with arising discontinuities in the function θ(r, φ) along some line within the disk. Then, according to Eq. (1), the energy of the sample would become infinitely large. Therefore, in the continuous approximation, all states under study are equally stable, regardless of the k value.

Energy (1) of the magnetic disk in the state with the topological charge k equals E = 2πk2Ahln(Rex/Rin). As a result, the energy of the sample will increase infinitely with Rex for any k ≠ 0. Thus, the above theory can be applied in practice exclusively for thin rings with Rex ≈ Rin (in this limiting case, we arrive at the results obtained in [5]), while only the homogeneous state of the magnetic material physically occurs in unbounded films with one hole. However, the situation changes radically when the film contains two holes rather than one. Let these holes be cylindrical antidots of radii R1 and R2, and their centers be separated by the distance a ≫ R1, R2 (Fig. 1). Then, since the equation Δθ = 0 is linear, its solution can be found as a superposition of the solutions obtained above for the film with one antidot: θ = k1φ1 + k2φ2, where φ1 and φ2 are the polar angles in the coordinate systems associated with the centers of the holes and k1 and k2 are integer topological charges. Consider the asymptotic behavior of the found solution at a large distance from the system, when r1 ≈ r2 = r ≫ a. In this case, φ1 ≈ φ2 = φ, so that θ = (k1 + k2)φ, and in the case of k1 + k2 ≠ 0, the energy of an infinite film is again infinite. To avoid this, we set k1 = k and k2 = −k. Then, we have

$$\theta = k({{\varphi }_{1}} - {{\varphi }_{2}}).$$
(2)
Fig. 1.
figure 1

Schematic of the film with two holes.

Full size image

Figure 1 clearly demonstrates that the difference of angles involved in this relation is equal to the angle at which the segment connecting the centers of holes is visible from a given point, so that θ ∼ r−1, and hence (∇θ)2 ∼ r−4, which ensures the convergence of inte-gral (1) in the range of large values of r. Thus, the energy of a magnetic material in the state under study is finite. A detailed calculation shows that it is equal to

$$E = 4\pi {{k}^{2}}Ah\ln (a{\text{/}}\sqrt {{{R}_{1}}{{R}_{2}}} ).$$
(3)

The distribution of magnetization near the holes, given by Eq. (2) at k = 1, is schematically shown in Fig. 1. The state with k = −1 is obtained from it as a mirror image; k = 0 corresponds to the uniformly magnetized sample. States with other values of k are not of interest for the further analysis.

3 DISCRETE MODEL

Passing to the lattice model [8], we consider a square lattice of spins, some sites of which are empty. Then, up to some factor, the energy of the magnetic material minus the energy of the homogeneous state has the form

$$E = \sum\limits_{i,j} (1 - \cos ({{\theta }_{i}} - {{\theta }_{j}})) + \sum\limits_i (1 - \cos {{\theta }_{i}}),$$
(4)

where the summation in the first term is carried out over all pairs of neighboring lattice sites along either the horizontal or the vertical direction. In the second term, the summation is performed over all sites located at the edge of the lattice. The second term, which is responsible for the unambiguous definition of the homogeneous state of the magnet (θi = 0), allows us to simulate the infinite length of the film: we assume that inhomogeneities are localized within the lattice, while all spins outside it are oriented in the same way.

We numerically optimize energy (4). Since all local minima of the system are of interest, we use the stochastic approach, in which the numerical optimization is repeated many times, starting from various random points. Further on, all found minima are ranked by energy values, and one solution is selected for each value (we assume that nonequivalent minima equal in magnitude can hardly exist). As a result of such a search for a lattice containing 188 spins, in addition to the homogeneous state with E = 0, we find a local minimum with E = 10.3. The corresponding distribution of magnetization is shown in Fig. 2. It is easy to see that it exactly reproduces the state with k = 1, which we predicted within the continuous model.

Fig. 2.
figure 2

Solitary inhomogeneity localized at two holes.

Full size image

Although the discrete model provides an independent confirmation of the suggested theory, this is not its main advantage. The energy given by Eq. (4) is limited not only from below but also from above; consequently, the transitions between any states of the lattice can provide only finite work. This allows us to estimate the stability of inhomogeneous states that are treated as metastable ones. Such an approach, used earlier in [5], made it possible to obtain nontrivial results for the case of a closed loop of spins (one-dimensional model). In the roughest approximation, we can consider the transformation θi → (1 − t)θi, which is continuous and relates the inhomogeneous state at t = 0 to the homogeneous state at t = 1. Then, E becomes a function of the parameter t, attains minima at both ends of the segment [0, 1], and, therefore, should also have a maximum within this segment. In our case, the value of this maximum appears to be Emax = 11.6. As a result, the work needed to destroy the inhomogeneous state is about Emax − E = 1.3. Finding out more complicated transformations using numerical methods, this estimate can be improved to 1.0; however, in any case, this value is about 10% of the energy of the inhomogeneity itself, which may indicate a good stability of the states under study with respect to thermal fluctuations.

4 EFFECT OF ELECTRIC CURRENT

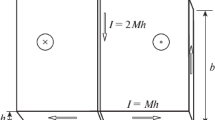
Let us demonstrate that inhomogeneities with k = ±1 localized at two holes can be stable under the effect of electric current flowing across one of the holes. Assume first that the magnitude of such a current is extremely high, so that the contribution of exchange interaction can be neglected. Then, at all points of the sample, the magnetization vector is oriented along the current-induced magnetic field lines, i.e., along tangents to circles whose centers coincide with the center of the hole. Thus, this hole will be characterized by a topological charge of +1, and the second one will be characterized by zero charge since the magnetization near it will be nearly constant. However, a decrease in the current is accompanied by an increase in the role of the exchange interaction whose energy, as known, decreases significantly when the total topological charge of the system is zero. Nevertheless, the electric current can still remain high enough to orient the magnetization near it along the magnetic field lines. Therefore, the topological charge corresponding to the first hole will retain its value of +1. Consequently, for the second hole, the topological charge is forced to become equal to  −1 owing to the spontaneous redistribution of magnetization. A further decrease in the current will cause the formation of a magnetization vortex around the first hole to become unfavorable, and the topological charges will vanish for both holes. Eventually, the magnetic material will transform to a state close to the homogeneous one. Thus, we expect that the state with topological charges +1 and −1 is stable at electric currents in a certain range. At the same currents, the state with charges −1 and +1 is also stable, but the current should be passed across the second hole.

Let us check our reasoning by a numerical experiment. For this purpose, we supplement Eq. (4) by the term

$${{E}_{I}} = - \sum\limits_i \frac{I}{{{{r}_{i}}}}\cos ({{\theta }_{i}} - {{\varphi }_{i}}),$$

where \(({{r}_{i}},{{\varphi }_{i}})\) are the polar coordinates of the sites in the reference system related to the point where the electric current passes across the plane. We chose this point at the center of one of the vacancies in the lattice. By optimizing the energy obtained at different values of the electric current I, we find three nonequivalent distributions of magnetization, which are shown in Fig. 3. In this case, all distributions correspond to the global energy minimum, so that for a given I value, these states are stable. However, the states of a similar topology at other currents may be metastable. The dependence of the energy E of each of them on the current I is shown in Fig. 4. As expected, the state with charges 0 and 0 is stable at I < 0.5, the stable state for I > 2.6 corresponds to the charges +1 and 0, and a solitary inhomogeneity characterized by charges of +1 and −1, which is of special interest, is stabilized at intermediate values 0.5 < I < 2.6.

Fig. 3.
figure 3

Magnetization distributions under the effect of electric current.

Full size image
Fig. 4.
figure 4

Energies of different states under the effect of electric current.

Full size image

5 CASE OF FOUR HOLES

It is clear that all procedures discussed above are applicable not only to the film with two antidots but also to films with a larger number N of such antidots. In this case, the relation similar to Eq. (2) should have the form \(\theta = {{k}_{1}}{{\varphi }_{1}} + {{k}_{2}}{{\varphi }_{2}} + \ldots + {{k}_{N}}{{\varphi }_{N}}\); hence, the condition \({{k}_{1}} + {{k}_{2}} + \ldots + {{k}_{N}} = 0\) ensuring a finite value of the energy of the system must be valid.

For example, consider the case of N = 4, placing the holes of equal radius R at the vertices of a square with the side a. By optimizing energy (4) for the corresponding lattice of 180 spins, we obtain the distributions of magnetization shown in Fig. 5 (signs plus and minus mark the holes having charges of +1 and −1, respectively). The energies of these states are E1 = 10.6 (two holes are coupled along the horizontal or vertical directions), E2 = 13.5 (two holes are coupled along the diagonal), and E3 = 15.9 (all four holes are coupled).

Fig. 5.
figure 5

Solitary inhomogeneities localized at four holes.

Full size image

From the viewpoint of the continuous model, the first two of the states obtained are described by Eq. (2) at k = 1, which means that their energies can be calculated by Eq. (3). Assuming that the distance between the centers of the holes for the second state is \(a\sqrt 2 \), we obtain E1 = 4πAhln(a/R) and \({{E}_{2}} = 4\pi Ah\ln (a\sqrt 2 {\text{/}}R)\). For the third state, it can be shown that E3 = \(8\pi Ah\ln (a{\text{/}}R\sqrt 2 )\). It is easy to see that this energy can be expressed in terms of the first two as E3 = 4E1 − 2E2. This relation can be used as a test one to check the correspondence between the continuous and discrete models. Substituting the previously found values E1 = 10.6 and E2 = 13.5 into the above relation, we obtain E3 = 15.4, which differs only by 3% from the calculated value.

Although the third of all inhomogeneities illustrated in Fig. 5 corresponds to the highest energy, it is of most interest because this structure actually represents a bound state of two inhomogeneities of the first type. This is confirmed by a nonzero binding energy E3 − 2E1 = −4πAhln2 < 0; consequently, it is particularly difficult to destroy such a state. To verify this, let us again turn to the minimum work required to transfer a discrete lattice of spins from a given state to the homogeneous state. In this case, a “rough” estimate using the transformation θi → (1 − t)θi gives quite an overestimated value of 12.5. This estimate can be improved down to 4.0, which is approximately 25% of the energy of inhomogeneity and is larger than similar work for the case of two holes by a factor of 4. Thus, coupling of four holes at once is apparently easier for actual implementation because of a higher relative stability of the resulting inhomogeneity. At the same time, its formation, as clear from Fig. 5 and from the above analysis of the effect of electric current, can be carried out by passing oppositely directed currents of a certain magnitude across two holes lying at the same diagonal of the square.

6 CONCLUSIONS

To summarize, we have shown that thin films with topological features in the form of several holes can form solitary magnetic inhomogeneities that are stable under the effect of electric current and metastable in its absence. In this case, however, even metastable states can be sufficiently long-lived owing to a significant energy barrier that should be overcome to destroy an inhomogeneity. Moreover, this barrier becomes finite only within the discrete model, the choice of specific parameters of which remains arbitrary to a certain extent. That is why, at the moment, it is impossible to reliably estimate the temperatures at which the described states can be observed in experiments. In our opinion, this theoretical problem primarily requires further study since the idea of stabilizing inhomogeneous structures involving topological factors underlies not only our work but also all studies of skyrmions. At the same time, topological consideration is inapplicable to physical systems of a fundamentally discrete nature, to which, in part, belong crystal lattices. The development of a consistent methodology for estimating the reliability of the constraints imposed by topology on the behavior of magnetic structures would greatly simplify the transition from theoretical predictions to their direct experimental verification.

Nevertheless, we believe in actual realizability of the heterogeneities described here. From a technical point of view, their important feature is their localization on a plane rather than in three-dimensional space, which makes their implementation possible in heterostructures with the thinnest layers. In addition, each pair of holes can encode more than one bit since the surrounding magnetic material exhibits either the homogeneous state or one of two inhomogeneous states that differ in the sign of the topological charge. Thus, it is quite likely that the use of films with topological features is the key to increasing the density of information recording, as well as to solving a number of other problems associated with the development of nanoelectronics.