INTRODUCTION

Observations of processes in the space plasma, which became possible after the launching of artificial Earth satellites, led to the discovery and intensive studies of new plasma phenomena one of which is auroral kilometric radiation (AKR). Auroral kilometric radiation was first detected on the Elektron-2 satellite in 1965 [1]. Its characteristic frequencies are too low to penetrate through the ionosphere to the ground. This radiation is generated because of the complex interaction of waves with particles in the auroral region (region with geomagnetic latitudes of 65°–85° depending on the geomagnetic activity where auroras are observed) owing to the free energy from the precipitating flux of accelerated auroral electrons (with an average energy of several keV). The geomagnetic latitude is similar to the geophysical latitude, but it is measured from the axis of the geomagnetic dipole rather than from the geophysical poles. The magnetic axis is inclined to the Earth’s rotation axis by ~11.5°. Auroral kilometric radiation is observed in the frequency range of 20–800 kHz near the local electron cyclotron frequency. It is known that AKR is enhanced during magnetic perturbations and correlates with the geomagnetic index АЕ [2], which is calculated from data of high-latitude ground-based magnetometers and reflects the current flowing in the ionosphere. To explain the generation of AKR, the cyclotron maser instability mechanism was proposed. This instability is developed in the auroral magnetosphere in regions with a low plasma density (cavities), where the electron plasma frequency is lower than the local electron cyclotron frequency [3].

In contrast to the equatorial and mid-latitude regions, the high-latitude region is characterized by comparatively low electron densities and is a strongly structured medium because of the presence of numerous inhomogeneities at different scales from meters to hundreds of kilometers, where AKR can be generated. Inhomogeneities appear because of (i) magnetosphere–ionosphere processes associated with the auroral activity, in particular, with the precipitations of high-energy particles, and (ii) processes of plasma transport and heating owing to the magnetospheric electric fields and instabilities of macroscopic current systems. These inhomogeneities cannot be studied through geomagnetic activity indices because they are averaged characteristics, whereas AKR can be an indicator of geomagnetic perturbations. Consequently, it is important to study and use AKR. Furthermore, the near-Earth plasma, as a natural laboratory, makes it possible to verify modern nonlinear theories of plasma processes.

To obtain slowly varying and averaged characteristics of AKR on satellites, one usually applies classical processing methods based on the Fourier transform and three-dimensional amplitude–frequency–time representations of the results of measurements. In this work, we propose a different approach because the auroral region is characterized by strong inhomogeneity and nonstationarity, which affect the results of measurement of AKR: the amplitude and phase of the signal fluctuate strongly at small scales. In this case, it is appropriate to use the fractal approach that does not involve the classical characteristics of the signal such as the amplitude, phase, and polarization. However, electromagnetic fields at different frequencies (correspondingly, altitudes) can be compared using such characteristics as scaling index, Hurst exponent, and fractals. Methods of nonlinear dynamics, in particular, the fractal description, have recently provided a convenient and efficient approach to solve various physical problems, including problems of space physics. This approach is based on self-similarity (scale invariance), which means that elements of the structure at different scales are similar to each other. A great advantage of the fractal method is the universality of results and their independence of the nature of fractal structures in the region under consideration.

In this work, AKR is used for the remote diagnostics of processes in the auroral magnetosphere. To the best of our knowledge, fractal approaches have not yet been applied to describe processes responsible for AKR. However, the authors of [4] studied short bursts of AKР depending on their intensity and demonstrated a power-law distribution observed in dynamic spectra of AKР, which indicates that the self-organized citicality concept is applicable to analyze the generation of AKР. In this study, AKR is applied for the remote monitoring of processes in the auroral region. Such an approach has advantages compared to in situ measurements because the altitude of a satellite over a source and the emission cone pattern determine the duration of satellite measurements of AKR at the constant flux of high-energy particles from the tail of the magnetosphere [5]. In this work, AKR is studied in detail in satellite data using nonlinear dynamics methods. To determine the dependence of the properties of the plasma on the altitude, we evaluate the spectrum of fluctuations of AKR at various frequencies, which corresponds to the altitude section. Then, knowing the scaling index, one can determine the fractal characteristics of the plasma in the region of generation of AKR and their dependence on the altitude.

It should be noted that the authors of [6, 7] obtained parameters describing the fractal geometry of the turbulent current sheet of the magnetotail near a nonequilibrium (quasi)steady state and proposed a topological scenario of a magnetospheric substorm. At the same time, using the nonlinear dynamics method, we analytical estimated in [8, 9] the observed scaling of fluctuations of electric fields and auroras in the auroral ionosphere and presented constraints imposed by the critical condition of percolation of Hall and Pedersen currents. The auroral magnetosphere, where charged particles are accelerated and AKR is generated, is an “intermediate” region between the magnetotail and high-latitude ionosphere, for which fractals parameters have not yet been obtained. It is important to fill this “gap.”

METHOD

As known, the presence of various frequencies and scales at different times, i.e., the nonstationarity of the signal, is a signature of turbulent and fluctuating fields. A wavelet transform which allows one to simultaneously obtain the frequency/scale and time distributions of the signal power is a natural method to study the frequency–time properties of nonstationary signals. The necessity of the application of the wavelet transform is also caused by a limited length of analyzed data series. According to the uncertainty principle, using the window Fourier transform, a significant localization of the signal power in time can be achieved only with the loss of frequency localization of the spectral function. This is also valid for the wavelet transform whose advantage is only a larger flexibility of wavelets used as the basis functions because the frequency–time windows in this case is not fixed. However, this makes it possible to simultaneously localize in time sharp gradients or discontinuities in the signal [10, 11]. Turbulence belongs to phenomena that have a complex irregular character, a large number of degrees of freedom, and a branched fine structure; it is difficult to describe them within an approach based on the solution of deterministic equations. However, these phenomena often demonstrate so-called complex behavior, which is characterized by a much smaller number of control parameters [12]. It is remarkable in the scale invariance of the dynamics of the system. One of the variants of the scale invariance is self-similarity manifested in power-law dependences of various characteristics of the system on the time (space) scale. The fractal geometry technique is a method of description of systems with self-similarity. A fractal can be considered as a stochastic object similar to time series having the self-similarity property [13], which is treated in the statistical sense: statistical characteristics measured at different scales are structurally similar.

The self-similarity of a time series \(X(t)\) means that \(X(at)\) is identical in distribution to \({{a}^{H}}X(t)\), \(\forall t \geqslant 0\), \(\forall a > 0\), where H is the Hurst exponent. The increment process \(\Delta X = X(k + t) - X(k)\), \(k \geqslant 0\) is called fractal Gaussian noise, is a stationary Gaussian process, and demonstrates a long-range dependence. Negative correlation between the increments of the random function \(X(t)\) (antipersistent process) exists in the case 0 < H < 0.5, whereas correlation between the increments is positive (persistent process) for the Hurst exponents 0.5 < H < 1. In the latter case, the corresponding fractal Gaussian noise demonstrates the long-range dependence. In general, the long-range dependence is a property of a certain class of stationary random processes such as fractal Gaussian noise obtained as increments of fractal Brownian motion with 0.5 < H < 1. Fractal Brownian motion is a Gaussian process with zero mean and stationary increments with \(H \in [0,1]\), which is considered as a natural expansion of the ordinary Brownian motion with H = 1/2.

The Abry–Veitch method [14, 15] allows one to detect, identify, and quantitatively estimate the scaling properties of data. Different manifestations of the scaling properties can be efficiently identified and quantitatively estimated within a unified approach based on the discrete wavelet transform of data. This efficiency is high significantly because wavelets used as the basis functions to analyze the signal are scaling invariant unlike many other basis functions. For this reason, the estimate of the scaling exponent obtained by the Abry–Veitch method is unbiased and has a small error [14]. The admissibility condition for the mother wavelet, as well as the requirement of zero first moments that is involved in the procedure of construction of some families of wavelets (e.g., Daubechies wavelets [16]), makes it possible to efficiently remove trends, i.e., nonrandom functions that are present in data and distort the actual scaling index.

The Abry–Veitch method was successively used in [17] to study turbulence in data of measurement of magnetic field variations in the plasma sheet of the magnetosphere, in [10, 18] to study of the scaling of electric fields in the polar cap and auroral region, in [19, 20] to reveal the scaling properties of auroras, and in [8, 21, 22] to describe the spatial structure of the ionospheric conductivity.

The detail wavelet coefficients \({{d}_{{j,k}}}\) at the scaling level j for the discrete wavelet transform of the stationary process \(X(t)\) can be obtained as

$${{d}_{{j,k}}}{{ = 2}^{{j/2}}}\sum\limits_{i = 1}^{{{n}_{j}}} {{X}_{i}}{{\psi }_{0}}{{(2}^{{ - j}}}n - k).$$
(1)

Here, \({{\psi }_{0}}\) is the basis wavelet and \({{n}_{j}}{{ = 2}^{{ - j}}}n\) is the number of wavelet coefficients at given \(j = 0,1,2,\;...\) called the permission level or octave. In the Abry–Veitch method [14, 15], the variance of detail wavelet coefficients is calculated for each octave j as

$${{\mu }_{j}} = \frac{1}{{{{n}_{j}}}}\sum\limits_{k = 1}^{{{n}_{j}}} {\text{|}}{{d}_{{j,k}}}{{{\text{|}}}^{2}}.$$
(2)

Further, the scaling exponent (index) α is estimated from the slope of the regression dependence of \({{y}_{j}} = \mathop {\log }\nolimits_2 ({{\mu }_{j}})\) on j (second-order scaling diagram or logarithmic diagram). The presence of linear segments on the resulting dependence indicates self-similarity. As mentioned above, in contrast to the traditional spectral method, this approach allows one to obtain an unbiased estimate of the scaling exponent α. The Hurst exponent H and fractal dimension D can be then determined in terms of the known scaling exponent α. The Hurst exponent is an important parameter in the theory of self-similar processes because it is an indicator of the self-similarity of a random process and characterizes the properties of the long-range dependence. The fractal dimension is usually treated as the Hausdorff–Besicovitch dimension [13].

RESULTS AND THEIR ANALYSIS

We analyzed data on the electromagnetic field measured on the Interball-2 satellite, which was launched on August 29, 1996, to a high-apogee orbit with the initial perigee of 769 km, apogee of 19 211 km, and inclination of 62.8°. The orbit of the Interball-2 satellite was such that it was in a single magnetic shell for a long time and AKR could be measured for several hours. These measurements allowed one to reveal the long-term evolution of processes in auroral regions, using AKR as a remote monitoring tool [11]. This approach has some advantages compared to in situ measurements for the study of long-period processes and is methodically close to optical measurements of aurora in the ionosphere in various spectral channels. In this work, we used the measurements of AKR for monitoring of the auroral region. Since the generation of AKR occurs at the local electron gyrofrequency, the dependence of the fractal properties on the altitude can be estimated.

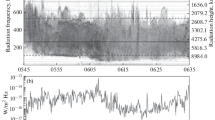
We consider data on AKR recorded on the Interball-2 satellite on November 22, 1997, at a moderate geomagnetic activity, AE ~ 500–600 nT, in the evening sector of the magnetosphere at ~19–20 MLT. The measurements were performed when the satellite moved at altitudes from 18 900 to 15 600 km with a maximum geomagnetic latitude of about 80°. The upper panel of Fig. 1 shows the dynamic spectrogram of AKR in the time interval of 05:36–06:36 UT. The integral intensity of radiation is higher in the time interval of 05:45–06:10 UT, where it was about 10‒15 W/(m2 Hz). The maximum intensity was observed at the frequency range of 119–539 kHz.

Fig. 1.
figure 1

(Color online) (Upper panel) Dynamic power spectrogram of auroral kilometric radiation according to data from the Interball-2 satellite on November 22, 1997. (Lower panel) Logarithmic diagram obtained using the Abry–Veitch method for a frequency of 323.584 MHz; according to this diagram, the scaling index is α = 0.317.

Full size image

For each frequency in the spectrum obtained on the satellite (it usually included 240 or 480 frequency channels) [23], we applied the Abry–Veitch method based on the wavelet transform, plotted logarithmic diagrams, and determined the scaling exponent α from them. For instance, the logarithmic diagram for a frequency of 323.584 MHz is shown in the lower panel of Fig. 1. In this case, the scaling exponent is α = 0.317. We used the Daubechies wavelets [16] to plot logarithmic diagrams. For further analysis, we took only values for which estimates of the goodness Q of the linear regression according to the χ2 criterion are ≥0.5. Correspondingly, only α values for which \(Q \geqslant 0.5\) are shown in the upper panel of Fig. 2 versus the frequency (or altitude). Knowing the frequency of AKR, the altitude where this radiation is generated can be estimated in the dipole approximation of the geomagnetic field. A value of 0.6 G was taken for the magnetic field on the surface because AKR is generated at high latitudes. The horizontal axis in Fig. 2 indicates both the frequency and altitude of generation of AKR. It is seen that the scaling exponent α increases with the altitude (or with a decrease in the frequency). It is important that \(\alpha \in [0;1]\), which means that the considered process with a finite dispersion exhibits long-range dependence [14]. There is a correlation between processes with self-similarity and processes with long-range dependence. Since processes with 0.5 < H < 1 exhibit long-range dependence, their spectral index is related to the Hurst exponent H as α = 2H – 1. Thus, it is possible to estimate the Hurst exponent: yj = log2(μj) ~ (2H – 1)j + const. Consequently, for the long-term dependence of the series with the Hurst exponent H, the plot of log2(μj) versus j has the slope α = 2H – 1. In our case, the Hurst exponent H is related to the fractal dimension D as D = 2 – H (Berry formula [24]).

Fig. 2.
figure 2

(Color online) (Upper panel) Scaling index α versus the altitude and frequency (only estimates of the goodness \(Q\) of the linear regression that satisfy the condition \(Q \geqslant 0.5\) are presented). (Lower panel) Fractal dimension D and Hurst exponent H versus the altitude and frequency.

Full size image

Generally, such a behavior of the fractal dimension and scaling exponent is characteristic of the region of generation of AKR. For example, Fig. 3 shows another case of AKR detected on October 13, 1997, also on the Interball-2 satellite; a similar procedure was used to process these measurements of AKR. The intensity of AKR in this case was an order of magnitude lower than that in the first case. The upper panel of Fig. 3 shows the dynamic frequency–time spectrogram of the power of AKR in the time interval of 08:39–11:29 UT. The dependences of the scaling exponent α on the frequency and altitude obtained by the Abry–Veitch method are shown in the middle panel of Fig. 3. The lower panel of Fig. 3 shows the dependences of the fractal dimension D and Hurst exponent H. It is seen again that the scaling exponent and Hurst exponent increases with the altitude, whereas the fractal dimension decreases with an increase in the altitude, which indicates the presence of long-range dependence.

Fig. 3.
figure 3

(Color online) (Upper panel) Dynamic power spectrogram of auroral kilometric radiation on October 13, 1997. (Middle panel) The scaling index α versus the altitude and frequency. (Lower panel) fractal dimension D and Hurst exponent H versus the altitude and frequency.

Full size image

It is known that repeating and reproducible conditions of observations are absent in the near-Earth medium, and the state of the auroral plasma has a complex dependence on many factors. This results in the inhomogeneity of the conditions of generation along magnetic field lines in the region of the auroral acceleration of particles. Nevertheless, there is a pronounced tendency to a decrease in the fractal dimension D with an increase in the altitude during generation of AKR signals. This tendency occurs possibly because the effect of upward fluxes from the ionosphere increases with a decrease in the altitude of generation of AKR. This in turn affects the increment of the cyclotron maser instability and changes conditions in the region of generation of AKR, which influences the scaling properties and self-similarity. In other words, the complex nonlinear interaction between the ionospheric and magnetospheric plasmas results in different conditions for the generation of AKR at different altitudes, which is manifested in change in the fractal characteristics obtained using the Abry–Veitch method.

The electron distribution function can affect the dependence of the scaling index on the altitude. When electron fluxes move toward the Earth to the region of an increase in the magnetic field, their pitch angles increase because of the conservation of the first adiabatic invariant. As a result, a peak at large pitch angles and a dip at small pitch angles appear in the electron distribution function, which results in a “horseshoe” distribution responsible for a more efficient transfer of the energy of electrons to waves. Furthermore, the plasma, fp, and cyclotron, fc, frequencies in most of the regions of the magnetosphere are related as fp/fc > 1, whereas the inverse relation fp/fc < 1 is valid in a relatively small region of the auroral magnetosphere where high-energy particles are accelerated and from which the electric field “removes” the background plasma. With a decrease in the altitude, the background plasma density increases so much that conditions for generation of AKR are violated, which determines the upper frequency bound of the radiation spectrum. In other words, the processes under consideration are nonstationary and inhomogeneous in altitude, which affects the development of the cyclotron maser instability and generation of AKR.

Although strongly different cases of AKR detected on the Interball-2 satellite were considered, our study revealed a self-similar process with a long-range dependence, i.e., a fractal Gaussian noise process with 0.5 < H < 1 and \(1.5 < D < 2\). Fractal noises are stochastic processes with a static dependence; i.e., their values at times even far from each other have a small but nonnegligible correlation. White noise is classically defined as a stochastic process with the spectral density independent of the frequency f and is written as \({{f}^{{ - 0}}}\). As a result, the integral and derivative of white noise have the spectral density \({{f}^{{ - \beta }}}\), where β is an integer (for flicker or pink noise, \({{f}^{{ - 1}}}\)). At the same time, fractal noises are defined as stochastic processes with the spectral density \({{f}^{{ - \beta }}}\), but β is not an integer and can be represented as 1 – 2H. (Classical white noise corresponds to H = 0.5.) Thus, electromagnetic fields observed during generation of AKR cannot be treated as colored noises such as flicker or white noise. We demonstrated for the first time scaling invariance in the AKR signal in the high-latitude region of the Earth. It is noteworthy that the previous observation of the scaling invariance of fluctuations of auroras [25] and the scaling properties in the auroral ionosphere [8] indicates that the scaling invariance can be due to the scaling in electromagnetic fields and fluxes of charged particles in the region of acceleration, which then lead to the structured aurora and conductivity.

CONCLUSIONS

To summarize, AKR has been used for the remote diagnostics of processes in the Earth’s magnetosphere. The fractal approach for the region of acceleration of charged particles in the auroral region has been applied for the first time. The fractal dimension and Hurst exponent in the region of generation of AKR have been determined, as well as their dependences on the frequency and altitude. Different cases of the detection of AKR under various geomagnetic conditions have been considered. In these cases, the intensities of AKR differ by an order of magnitude, but a stable tendency of a decrease in the fractal dimension with an increase in the altitude has been observed during generation of AKR. Furthermore, the determined scaling and fractal parameters clearly indicate that the processes under consideration are self-similar and involve long-range dependence. This most likely shows that the properties of the process (development of the cyclotron maser instability) of generation of AKR vary slightly.