INTRODUCTION

The idea of creating a quasi-stationary plasma accelerator (QSPA) and theoretical foundations of its functioning were formulated by A.I. Morozov in 1959 [1]. Based on the QSPA, it is possible to create an electrojet engine (EJE) that operates in a pulse–periodic mode with a power of several hundred kilowatts [1], provided that the almost complete ionization of the gas supplied to the accelerator is achieved. In particular, in order to use the QSPA as an EJE, it is necessary to coordinate the gas flow duration at the accelerator entrance with a discharge current duration that, as was shown in [2], may be up to 1 ms depending on the operating mode of the accelerator. Therefore, it is required to create gas flows of millisecond duration.

As noted in theoretical [1, 3] and experimental [4, 5] studies, the plasma stream regime in the accelerator channel depends on the flow rate of the working substance; i.e., it is determined by the local values of the density and velocity of the gas supplied to the accelerator inlet. This means that, in order to optimize the accelerator operation for obtaining a homogeneous high-speed plasma stream, it is necessary to have a tool for analyzing the gas flow created by a pulsed high-speed valve. This study is devoted to the development of a method for measuring spatial and time distributions of the gas flow density and velocity during a characteristic time interval of up to 1 ms.

EXPERIMENTAL TECHNIQUE

The method is based on the use of frame-by-frame gas flow interferometry in combination with the dynamic pressure measurements with a high-frequency sensor. The radial distribution of the gas flow density with a time resolution corresponding to the frame rate of a high-speed camera is determined from interferograms. According to the density values and the readings of the dynamic pressure sensor, the distribution of the gas flow velocity with the same temporal resolution is calculated.

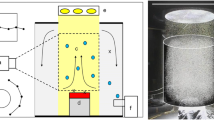
To perform these measurements, an experimental setup was created; its scheme is shown in Fig. 1. The vacuum chamber 1 was pumped out to a residual pressure of 10–4 mbar, and the pulsed gas puffing was performed by a high-speed electromagnetic valve 2 mounted at the end of the vacuum chamber. The gas entered the vacuum chamber through the valve openings located over a circle with an 8-cm diameter. A cylindrical insert 3 that imitated the shape of the QSPA gas channel was installed at the base of the valve inside the vacuum chamber. The length of the insert was 17 cm, and its diameter was 9 cm. The radiation generated by a Cobolt Samba 1500 semiconductor laser (6) with a wavelength of λ = 532 nm was used for probing. The laser beam was expanded by a specially designed system of two telescopes 8 and 9 to a diameter of 10 cm. To increase the sensitivity of this technique, a two-pass Fizeau interferometer was used as the interferometer; its basic elements are a separating mirror 7 and interference mirrors 10 and 11. Interference windows 4 and 5 that are fixed on nipples of the vacuum chamber made it possible to observe the interference of the gas flow with minimum parasitic distortions. The interference pattern was recorded using a high-speed Phantom v2512 (12) camera. In the experiments, the camera was set to a resolution of 1280 × 800 pixels, a frame rate of 25 kHz, and an exposure of 3 μs. A high-frequency PCB 113V28 dynamic pressure sensor (13) was mounted on a movable vacuum feedthrough, whose sequential movement perpendicular to the gas flow axis made it possible to determine the radial pressure distribution. The diameter of the sensitive element of the sensor is 5.5 mm, and the signal rise time was shorter than 1 μs.

Fig. 1.
figure 1

Scheme of the experimental setup: (1) vacuum chamber; (2) electromagnetic valve; (3) cylindrical insert; (4, 5) interference windows; (6) semiconductor laser; (7) separating mirror; (8, 9) telescopes; (10, 11) semitransparent interference mirrors; (12) high-speed camera; and (13) pressure sensor.

Full size image

The diagnostic region in the experiment was limited to the diameter of probing radiation, which was ~10 cm. The results presented in this article describe the studies of the helium flow and the distributions of the gas density and velocity in the cross section perpendicular to the flow axis at a distance of 4 cm from the cylindrical insert.

TECHNIQUE FOR PROCESSING THE EXPERIMENTAL DATA

The experiment included a sequence of separate starts of the electromagnetic valve. For each start, approximately 60 frames of the interference pattern were recorded, including the moments before and after the passage of the gas flow through the interference region. For each frame, the shift of the centers of the interference fringes relative to their initial positions on the reference frame was determined. The reference frame is the last frame preceding the appearance of the gas flow in the interference region. An undisturbed interference area was also present in each of the frames, which made it possible to eliminate the error in determining the order of the interference fringe shift.

Figure 2 shows a frame of the interference pattern during the passage of the gas flow through the registration region; the gas propagated from right to left. The cylindrical insert 1 is marked on the right; the high-frequency dynamic pressure sensor 2 is on the left. The interference area of the gas flow 3 and the undisturbed interference area 4 are also marked. The distance between the dashed line 5 marked in Fig. 2 and the cylindrical insert is 4 cm. Approximately 20 equidistant points were selected along the dashed line. For each of them, a rectangular area was determined with a height equal to the diameter of the sensitive element of the pressure sensor and a width covering the vertices of two adjacent interference fringes. This region was used to calculate the shift of the center of the interference fringe closest to the dashed line in pixels and to convert the shift in pixels into a phase shift. A typical calculation region of one point is marked in Fig. 2 with a white rectangle 6. Its enlarged images are shown in Figs. 3a and 3b. Figure 3a corresponds to the reference frame, while Fig. 3b is the frame with the largest shift of the interference fringes. The dashed lines in Figs. 3a and 3b mark the centers of the interference fringes.

Fig. 2.
figure 2

Frame of the interference pattern: (1) cylindrical insert; (2) sensitive element of the pressure sensor; (3) interference region of the gas flow; (4) unperturbed interference region; (5) line along which measurements were performed; and (6) calculation area of one point.

Full size image
Fig. 3.
figure 3

Enlarged calculation areas of one point (dashed lines indicate the centers of interference fringes, the values along the axes are indicated in pixels): (a) reference frame and (b) frame with the largest shift of the interference fringes.

Full size image

Thus, for each of the points of the investigated cross section, information on the dynamics of the phase shift of the interference fringe that was closest to it was obtained. Figure 4 shows the dynamics of the phase shift of the centers of the interference fringes for several points. The distances from the gas flow axis to the corresponding point are indicated on the right; the average error in determining the shift of the center of the interference fringe is shown on the left. The approximate value of the averaged error is 5°. The time was read from the moment the current was fed to the coil of the electromagnetic gas valve.

Fig. 4.
figure 4

Dynamics of the phase shift of the centers of the interference fringes at different distances from the gas flow axis.

Full size image

The results presented in Fig. 4 are the values of the phase shifts accumulated along the chord at a distance of z = 4 cm from the cylindrical insert. The further task was to recalculate these values into the radial distributions of the change in the refractive index. The relationship between the phase shifts accumulated along the chord and the change in the refractive index in the case of a cylindrical symmetry of the gas flow is described by the Abel equation:

$${{\Delta \varphi }}\left( {r,z} \right) = \frac{{8{{\pi }}}}{{{\lambda }}}\mathop \smallint \limits_r^R {{\Delta }}n\left( {{{\rho }},z} \right){{\;}}\frac{{{{\rho }}d{{\rho }}}}{{\sqrt {({{{{\rho }}}^{2}} - {{r}^{2}})} }},$$
(1)

where \({{\Delta \varphi }}\left( {r,~z} \right)\) and \({{\Delta }}n\left( {r,~z} \right)\) are the phase shift and the change in the refractive index at the distance r from the flow axis and at the distance z from the cylindrical insert, λ is the wavelength of probing radiation, and R is the gas flow radius.

The solution of Eq. (1) involves the reconstruction of the integrand \({{\Delta }}n\left( {r,z} \right)\). An example of the initial data for the calculation is shown in Fig. 5. This dependence is the radial distribution of the phase shift accumulated along the chord for a time moment of 618 μs, when the maximum concentration in the flow was observed. The most common methods for solving the Abel equation are direct methods. As noted in [6], the most reliable one among them is the Bockasten method [7]. Figure 6a shows the radial distribution of the change in the refractive index calculated using this method for a time of 618 μs. The relative error on the gas flow axis was 178% in this case.

Fig. 5.
figure 5

Radial distribution of the phase shift accumulated along the chord for an instant of time of 618 μs.

Full size image
Fig. 6.
figure 6

Radial distributions of the refractive index change for an instant of time of 618 μs: (a) Bokasten method and (b) Turchin statistical regularization method.

Full size image

The reason for large errors, as noted in [6], may be hidden in the solution of Eq. (1) without using regularization procedures. The most natural method for solving Eq. (1) using regularization is the Turchin statistical regularization method [8]. This method requires introducing a priori information on the smoothness of the desired function \({{\Delta }}n\left( {r,z} \right)\) and the characteristics of the input “noise.” In this paper, it was assumed that \({{\Delta }}n\left( {r,z} \right)\) has a first-order derivative and the input “noise” has a normal distribution.

The Turchin statistical regularization implies the replacement of Eq. (1) with the problem of minimizing the functional of \({{\Delta }}n\left( {r,~z} \right)\):

$$\begin{gathered} \left\| {\frac{{8{{\pi }}}}{{{\lambda }}}\mathop \smallint \limits_r^R {{\Delta }}n\left( {x,z} \right){{\;}}\frac{{xdx}}{{\sqrt {({{x}^{2}} - {{r}^{2}})} }} - ~{{\Delta \varphi }}\left( {r,z} \right)} \right\| \\ + \;{{\alpha }}\mathop \smallint \limits_r^R {{\left( {\frac{{d{{\Delta }}n\left( {x,z} \right)}}{{dx}}} \right)}^{2}}dx = {\text{min}}, \\ \end{gathered} $$
(2)

where α is the regularization parameter.

The larger α is, the greater is the weight of the second term and a smoother solution of problem (2) is obtained. The regularization parameter α was found as the value at which the logarithm of the a posteriori probability density \(P({{\alpha |\Delta \varphi }})\) approaches its maximum. This choice of α corresponds to the most probable solution \({{\Delta }}n\left( {r,z} \right)\). Figure 6b shows the radial distribution of the change in the refractive index obtained using the Turchin statistical regularization method for a time of 618 μs. In this case, the relative error on the flow axis was 37%.

As can be seen from Figs. 6a and 6b, the method of Turchin statistical regularization with the same initial data (see Fig. 5) leads to smaller errors. The dynamics of changes in the refractive index calculated using this method is shown in Fig. 7. The distances from the selected points to the gas flow axis are indicated on the right.

Fig. 7.
figure 7

Dynamics of changes in the refractive index at different distances from the gas flow axis.

Full size image

The data on the dynamics of changes in the refractive index obtained in this way were used to calculate the gas flow density dynamics. The relationship between the refractive index and the gas flow density is described by the Lorentz–Lorenz formula:

$$\frac{{{{n}^{2}} - 1}}{{{{n}^{2}} + 2}}\frac{1}{{{\rho }}} = q,$$
(3)

where n is the refractive index, ρ is the gas flow density, and q is the specific refraction of the gas.

The dynamics of the gas flow density calculated using formula (3) is shown in Fig. 8. The distances from the selected points to the gas flow axis are indicated on the right.

Fig. 8.
figure 8

Dynamics of the gas flow density at different distances from its axis.

Full size image

To calculate the dynamics of the gas flow velocity, in addition to the density at different points, the flow pressure must be known. Estimates of the gas flow velocity showed that, in this case, a supersonic gas flow took place. The relationship between the gas velocity, pressure, and density in this case is described by the formula [9]:

$$p - {{p}_{{{\text{fl}}}}} = \frac{2}{{k + 1}}{{\rho }}{{{v}}^{2}},$$
(4)

where p is the sensor-registered pressure, pfl is the flow pressure, ρ is the flow density, \({v}\) is the flow velocity, and k = 1.66 is the adiabatic index for helium. In this case, it was assumed that pfl is approximately \({{\rho }}{{{v}}^{2}}\). In this case, the velocity is expressed by the formula

$${v} = \sqrt {\frac{{k + 1}}{{k + 3}}\frac{p}{{{\rho }}}.} $$
(5)

The data on the pressure dynamics of the gas flow, as mentioned earlier, were obtained using a high frequency dynamic pressure sensor. For each start of the valve, the pressure dynamics for one point was recorded, and the complete picture was obtained via the sequential movement of the sensor and valve starts. Figure 9 shows the dynamics of the gas flow pressure at different distances from its axis. The maximum pressure was observed at a distance of 12 mm from the flow axis.

Fig. 9.
figure 9

Dynamics of the gas flow pressure at different distances from its axis.

Full size image

Figure 10 shows the dynamics of the gas flow velocity calculated for several points using formula (4). It was possible to calculate the velocity with acceptable accuracy within the time range from 420 to 1020 μs, when the values of the flow density and dynamic pressure significantly exceed the error of their determination. As can be seen in Fig. 10, the flow velocity decreases with time; however, at some instants of time, increases in the velocity that were associated with the features of the valve operation were observed.

Fig. 10.
figure 10

Dynamics of the gas flow velocity at different distances from its axis.

Full size image

Figures 11 and 12 demonstrate the time dependences of the density and velocity, as well as the dependences of the gas flow pressure and velocity, at a distance of 12 mm from its axis.

Fig. 11.
figure 11

Dynamics of the gas flow density and velocity at a distance of 12 mm from its axis.

Full size image
Fig. 12.
figure 12

Dynamics of the gas flow pressure and velocity at a distance of 12 mm from its axis.

Full size image

Thus, the developed technique made it possible to calculate the spatial and temporal distributions of the helium flow density and velocity of millisecond duration. The diagnostic region is limited by the diameter of probing radiation with a value of ~10 cm. In the present configuration of this setup, the minimum recorded values of the gas flow density and velocity are determined by the experimental errors that were equal to 0.0001 kg/m3 and 400 m/s, respectively. For a more detailed study of the characteristics of the gas flow, it is possible to increase the spatial and time resolution. Increasing the distance between the camera and the separating mirror (see Fig. 1) allows for increasing the spatial resolution by reducing the diagnostic region. The same effect can be achieved by broadening the interference fringes. Due to the wide range of settings of the Phantom v2512 high speed camera, one can change the time resolution in addition to the spatial resolution. The maximum resolution of the camera is 1280 × 800 pixels at a frame rate of 25 kHz; the maximum frame rate is 1 MHz at a resolution of 128 × 16 pixels.