On the Existence of a Periodic Mode in a Nonlinear System

Abstract

We consider a nonlinear control system with a bang-bang hysteresis control, which is a simplified model of a thermal energy harvester. We obtain conditions on the controller and the system parameters guaranteeing the existence of a periodic mode in the system.

INTRODUCTION

The paper [1] dealt with the nonlinear control system

$$ \begin {gathered} m\ddot y(t)+\beta \dot y(t)+k y(t)=\alpha l^{-1}E\big (T(t)\big )\big (\Delta -y(t)\big )-m g, \\ {\alpha }{\gamma ^{-1}}\dot T(t)+T(t)=u \end {gathered}$$

(1)

on the half-line $t\geq 0$ with the initial conditions

$$ y(0)=y_0,\quad \dot y(0)=0,\quad T(0)=T_0 $$

(2)

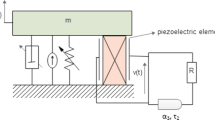
and the bang-bang hysteresis feedback control (Fig. 1)

$$ u=u_r\big (y(t)\big )= \begin {cases} \overline {u} & \text {if }y(t)\leq y_1 \\ \underline {u} & \text {if }y(t)\geq y_2 \\ \overline {u} & \text {if }y(\tau )\in (y_1,y_2)\text { for all }\tau \in [0,t] \\ \overline {u} & \text {if }y(t)\in (y_1,y_2)\text { and there exists an }s\in [0,t) \\ {} & \text {such that }y(s)=y_1\text { and }y(\tau )\in (y_1,y_2)\text { for all }\tau \in (s,t]\\ \underline {u} & \text {if }y(t)\in (y_1,y_2)\text { and there exists an }s\in [0,t) \\ {} & \text {such that }y(s)=y_2\text { and }y(\tau )\in (y_1,y_2)\text { for all }\tau \in (s,t]. \end {cases} $$

(3)

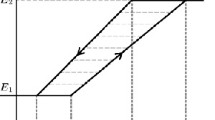
System (1) is a simplified model of a thermal energy harvester [2], where the following notation is used: $y$ is an output variable characterizing the strain of a shape memory material [3] with $0<y_0<\Delta$; $T$ is the material temperature with $T_0\geq 0$; the positive numbers $m$, $\beta$, $k$, $\alpha$, $l$, $\Delta$, and $\gamma$ are physical parameters of the thermal energy harvester; $g$ is the acceleration due to gravity; $u$ is an output feedback control ($u=u(y)$); and $E$ is the material Young modulus, which is described by a nonlinear characteristic with hysteresis and saturation (see Fig. 2).

Fig. 1.

Bang-bang feedback control.

Fig. 2.

Possible characteristic $E(T)$ with hysteresis.

The mapping $E(T)$ can be viewed as a set-valued mapping $E:\overline {\mathbb {R}}_{+}\to \overline {\mathbb {R}}_{+}$,

$$ E(T)=\begin {cases} E_1 & \text {if}\ \ T\leq M_1\\[1ex] \bigg [E_1,\dfrac {T-M_1}{M_2-M_1}(E_2-E_1)+E_1\bigg ] & \text {if}\ \ \begin {cases} M_2<A_1\\ T\in (M_1,M_2]\end {cases}\\[3ex] \bigg [\dfrac {T-A_1}{A_2-A_1}(E_2-E_1)+E_1,\dfrac {T-M_1}{M_2-M_1}(E_2-E_1)+E_1\bigg ] & \text {if}\ \ \begin {cases} A_1\leq M_2 \\ T\in (A_1,M_2]\end {cases}\\[3ex] [E_1,E_2] & \text {if}\ \ \begin {cases} M_2<A_1\\ T\in (M_2,A_1]\end {cases}\\[3ex] \bigg [\dfrac {T-A_1}{A_2-A_1}(E_2-E_1)+E_1,E_2\bigg ] & \text {if}\ \ \begin {cases} M_2<A_1\\ T\in (A_1,A_2]\end {cases}\\[3ex] \bigg [\dfrac {T-A_1}{A_2-A_1}(E_2-E_1)+E_1,E_2\bigg ] & \text {if}\ \ \begin {cases} A_1\leq M_2\\ T\in (M_2,A_2]\end {cases}\\[3ex] E_2, & \text {if}\ \ T>A_2. \end {cases} $$

Here $A_1$, $A_2$, $M_1$, $M_2$, $E_1$, and $E_2$ are positive constants determined by the physical properties of the shape memory material. In what follows, we assume that these constants are related by the inequalities

$$ 0<A_1<A_2,\quad 0<M_1<M_2,\quad M_1<A_1,\quad M_2<A_2,\quad 0<E_1<E_2.$$

Note that, given a specific continuous function $T(t)$, a single-valued branch of $E(T)$ is selected, which is a continuous function ranging in the interval $[E_1,E_2]$ (see [1]).

We assume that the threshold values $y_1$ and $y_2$ characterizing the control (3) satisfy the condition $0<y_1<y_2<\Delta$.

Efficiently verifiable conditions on the coefficients and initial values of the state variables in system (1), (2) and on the parameters of the controller (3) ensuring the onset of oscillatory motions [4, pp. 10] in the closed-loop system were obtained in [1], where the following definition of oscillatory motion (oscillatory mode) was used. A solution of system (1), (2), that is, a pair of functions $(y(t),T(t))$ satisfying the system and the initial conditions with the control $u$ given by (3) is called an oscillatory mode if there exist positive constants (mode parameters) $t^*_1$, $t^*_2$, $\underline {y}$, and $\overline {y}$ (where $0<t^*_1<t^*_2$ and $0<\underline {y}<\overline {y}<\Delta$) such that the following conditions are satisfied:

• 1. There exists a $t\geq 0$ such that $y(t)=\overline {y}$.

• 2. For each $t$ such that $y(t)=\overline {y}$, there exists a $\xi \in [t+t^*_1,t+t^*_2]$ such that $y(\xi )=\underline {y}$ and $y(\tau )\ne \underline {y}$ for all $\tau \in ({t,t+t^*_1})$.

• 3. For each $t$ such that $y(t)=\underline {y}$, there exists a $\xi \in [t+t^*_1,t+t^*_2]$ such that $y(\xi )=\overline {y}$ and $y(\tau )\ne \overline {y}$ for all $\tau \in ({t,t+t^*_1})$.

An analysis of the results in [1] shows that the problem of finding conditions on the parameters of the closed-loop system (1)–(3) guaranteeing the existence of oscillatory modes turns out to be very difficult. However, from the viewpoint of applications, the problem of determining conditions for the existence of a periodic mode in the closed-loop system is more important.

In the present paper, based on the results in [1], we obtain sufficient conditions for the existence of a periodic mode in the closed-loop system (1)–(3).

1. STATEMENT OF THE PROBLEM

We write system (1), (2) in the normal Cauchy form

$$ \begin {array}{l} \dot x_1(t)=x_2(t),\\[1ex] \dot x_2(t)=-\biggl (\dfrac {k}{m}+\dfrac {\alpha }{lm}E\big (x_3(t)\big )\biggr ) x_1(t) -\dfrac {\beta }{m}x_2(t)-g+\dfrac {\alpha }{lm}\Delta E\big (x_3(t)\big ),\\[3ex] \dot x_3(t)=-\dfrac {\gamma }{\alpha } \big (x_3(t)-u\big ),\\[2ex] x_1(0)=y_0,\quad x_2(0)=0,\quad x_3(0)=T_0,\quad \end {array} $$

(4)

where $x_1=y$, $x_2=\dot y$, $x_3=T$, $0<y_0<\Delta$, and $T_0\geq 0$.

The corresponding closed-loop system with the controller (3) for $t\geq 0$ has the form

$$ \begin {array}{l} \dot x_1(t)=x_2(t),\\[1ex] \dot x_2(t)=-\biggl (\dfrac {k}{m}+\dfrac {\alpha }{lm}E\big (x_3(t)\big )\biggr ) x_1(t) -\dfrac {\beta }{m}x_2(t)-g+\dfrac {\alpha }{lm}\Delta E\big (x_3(t)\big ),\\[3ex] \dot x_3(t)=-\dfrac {\gamma }{\alpha } \Big (x_3(t)-u_r\big (x_1(t)\big )\Big ),\\[2ex] x_1(0)=y_0,\quad x_2(0)=0,\quad x_3(0)=T_0, \end {array} $$

(5)

where $0<y_0<\Delta$ and $T_0\geq 0$; we assume that $y_0<y_1$ and $T_0<M_1$. We write the closed-loop system (5) in the vector form

$$ \dot x(t)=P\big (x(t),u_r\big ),\quad x=\big (x_1,x_2,x_3\big )^{\mathrm {T}}.$$

Now we say that the system

$$ \dot x(t)=P\big (x(t),\overline {u}\big ) $$

(6)

is active if the bang-bang relay output is $\overline {u}$ and the system

$$ \dot x(t)=P\big (x(t),\underline {u}\big ) $$

(7)

is active if the bang-bang relay output is $\underline {u}$.

Then the solution of the closed-loop system (5) with the initial conditions $x(0)=(y_0,0,T_0)^{\mathrm {T}}$, $y_0<y_1$, is sought in the class of continuous vector functions $x(t)$ in accordance with the following algorithm of active mode alternation:

$$ \dot x(t)=\begin {cases} P\big (x(t),\overline {u}\big ) & \text {if }x_1(t)\leq y_1\\ P\big (x(t),\underline {u}\big ) & \text {if }x_1(t)\geq y_2\\ P\big (x(t),\overline {u}\big ) & \text {if }x_1(t)\in (y_1,y_2)\text { and there exists an }s\in [0,t) \\ & \text {such that }x_1(s)=y_1\text { and }x_1(\tau )\in (y_1,y_2)\text { for all }\tau \in (s,t]\\ P\big (x(t),\underline {u}\big ) & \text {if }x_1(t)\in (y_1,y_2)\text { and there exists an }s\in [0;t)\\ & \text {such that }x_1(s)=y_2\text { and }x_1(\tau )\in (y_1,y_2)\text { for all }\tau \in (s,t]. \end {cases} $$

(8)

Here the solutions of systems (6) and (7) are matched by continuity at the points of discontinuity of the right-hand side of the system (on the hyperplanes $x_1=y_1$ and $x_1=y_2$). In what follows, a function $f$ defined on the half-line $t\ge 0$ is said to be $\Theta$-periodic if $f(t+\Theta )=f(t)$ for all $t\ge 0$.

Now let us state a control problem for system (4).

Problem.

Find constraints on the number parameters $m$, $k$, $\alpha$, $l$, $\beta$, $\Delta$, and $\gamma$ of system (4) as well as on the parameters $y_1$, $y_2$, $\underline {u}$, and $\overline {u}$ of the controller (3) under which there exists a periodic solution (periodic mode) in the closed-loop system (5).

2. PERIODIC MODE IN SYSTEM WITH PROGRAMMED CONTROL

We divide the solution of the problem about the existence of a periodic solution in system (5) into several steps. First, we study the existence of a periodic solution of system (4) with the programmed control

$$ u_p(t)= \begin {cases} \overline {u} & \text {if}\ \ t\in [q\Theta , q\Theta +\Theta _1) \\ \underline {u}, & \text {if}\ \ t\in [q\Theta +\Theta _1, q\Theta +\Theta _1+\Theta _2), \end {cases} \quad q=0,1,2,\ldots ;\quad \Theta _1+\Theta _2=\Theta .$$

(9)

Here $\overline {u}$, $\underline {u}$, $\Theta _1$, and $\Theta$ are positive parameters of the programmed control.

Now consider the problem of finding control parameter values ensuring the existence of a periodic solution of the closed-loop system (4), (9).

First, note that this control $u(t)$ is a piecewise constant $\Theta$-periodic function. Let us show that the equation

$$ \dot x_3(t)=-\frac {\gamma }{\alpha } \big (x_3(t)-u_p(t)\big )$$

(10)

has a $\Theta$-periodic solution for any $\overline {u}$, $\underline {u}$, and $\Theta >\Theta _1>0$. Indeed, the Cauchy formula

$$ x_3(t)=x_3(s) e^{-\gamma (t-s)/\alpha } +\int _s^t e^{-\gamma (t-\tau )/\alpha }\frac {\gamma }{\alpha } u(\tau )\thinspace d\tau $$

(11)

holds for the solutions of Eq. (10) for any $t\geq s\geq 0$. Let $x_3(0)=T_0$. Since $u_p(t)\equiv \overline {u}$ on the interval $[0,\Theta _1)$, it follows from (11) that

$$ \begin {aligned} x_3(\Theta _1)&=T_0 e^{-\gamma \Theta _1/\alpha } +\frac {\gamma }{\alpha }\overline {u}\int _0^{\Theta _1} e^{-\gamma (\Theta _1-\tau )/\alpha } \thinspace d\tau \\ &=T_0 e^{-\gamma \Theta _1/\alpha } +\overline {u} (1-e^{-\gamma \Theta _1/\alpha })= \overline {u}+(T_0-\overline {u}) e^{-\gamma \Theta _1/\alpha }. \end {aligned} $$

(12)

Further, since $u_p(t)\equiv \underline {u}$ on the interval $[\Theta _1,\Theta )$, we obtain

$$ \begin {aligned} x_3(\Theta )&=\underline {u}+\big (x_3(\Theta _1)-\underline {u}\big ) e^{-\gamma \Theta _2/\alpha } =\underline {u}+ \left (\overline {u}+(T_0-\overline {u}) e^{-\gamma \Theta _1/\alpha } -\underline {u}\right ) e^{-\gamma \Theta _2/\alpha } \\ &= \underline {u}(1-e^{-\gamma \Theta _2/\alpha })+ \overline {u}(1-e^{-\gamma \Theta _1/\alpha })e^{-\gamma \Theta _2/\alpha } +T_0 e^{-\gamma \Theta /\alpha }. \end {aligned} $$

(13)

In view of the $\Theta$-periodicity of the function $u_p(t)$, we conclude that the solution $x_3(t)$ is $\Theta$-periodic if and only if $x_3(\Theta )=T_0$. Then we find the initial condition for the $\Theta$-periodic solution $x^{\Theta }_3(t)$ from the representation (13),

$$ T_0=\underline {T}=\frac { \underline {u}(1-e^{-\gamma \Theta _2/\alpha })+ \overline {u}(1-e^{-\gamma \Theta _1/\alpha })e^{-\gamma \Theta _2/\alpha } }{1-e^{-\gamma \Theta /\alpha }}. $$

(14)

It follows from (13) and (14) that

$$ x^{\Theta }_3(\Theta _1)=\frac { \overline {u}(1-e^{-\gamma \Theta _1/\alpha })+ \underline {u}(1-e^{-\gamma \Theta _2/\alpha })e^{-\gamma \Theta _1/\alpha } }{1-e^{-\gamma \Theta /\alpha }}.$$

Now we set $\overline {T}=x^{\Theta }_3(\Theta _1)$ and $\hat \gamma =\gamma /\alpha$ and write the $\Theta$-periodic solution of Eq. (10) in closed form,

$$ x^{\Theta }_3(t)= \begin {cases} \overline {u}+(\underline {T}-\overline {u})e^{-\hat \gamma (t-q\Theta )} &\text {if}\ \ t\in [q\Theta , q\Theta +\Theta _1) \\ \underline {u}+(\overline {T}-\underline {u})e^{-\hat \gamma (t-q\Theta -\Theta _1)} &\text {if}\ \ t\in [q\Theta +\Theta _1,q\Theta +\Theta ), \end {cases}\quad q=0,1,2,\ldots $$

Now assume that the parameters $\overline {u}$, $\underline {u}$, $\Theta _1$, and $\Theta$ of the controller (9) have been chosen so that

$$ \underline {T}<M_1,\quad \overline {T}>A_2. $$

(15)

Assuming that the component $x_3$ of the solution of the closed-loop system (4), (9) satisfies the initial condition $x_3(0)=\underline {T}$, consider the subsystem

$$ \begin {array}{l} \dot x_1(t)=x_2(t),\\[1ex] \dot x_2(t)=-\biggl (\dfrac {k}{m}+\dfrac {\alpha }{lm}\varphi (t)\biggr ) x_1(t) -\dfrac {\beta }{m}x_2(t)-g+\dfrac {\alpha }{lm}\Delta \varphi (t),\\[2ex] x_1(0)=y_0,\quad x_2(0)=0,\end {array}$$

(16)

where $\varphi (t)=E(x_3^{\Theta }(t))$. By virtue of conditions (15) and the fact that $x_3^{\Theta }(t)$ is a $\Theta$-periodic solution of Eq. (10), the function $\varphi (t)$ will be $\Theta$-periodic as well, and we can write

$$ \varphi (t)=\begin {cases} E_1, & t\in [q\Theta , q\Theta +\Theta _{A_1}) \\ \dfrac {\overline {u}+(\underline {T}-\overline {u})e^{-\hat \gamma (t-q\Theta )}-A_1}{A_2 -A_1}(E_2-E_1)+E_1, &t\in [q\Theta +\Theta _{A_1}, q\Theta +\Theta _{A_2}) \\ E_2, & t\in [q\Theta +\Theta _{A_2}, q\Theta +\Theta _1) \\ E_2, & t\in [q\Theta +\Theta _1, q\Theta +\Theta _{M_2}) \\ \dfrac {\underline {u}+(\overline {T}-\underline {u})e^{-\hat \gamma (t-q\Theta -\Theta _1)} - M_1}{M_2-M_1}(E_2-E_1)+E_1, &t\in [q\Theta +\Theta _{M_2} q\Theta +\Theta _{M_1}) \\ E_1, & t\in [q\Theta +\Theta _{M_1}, q\Theta +\Theta ), \\ \end {cases} $$

(17)

where

$$ \begin {aligned} \Theta _{A_1}&=\frac {1}{\hat \gamma }\ln \frac {\underline {T}-\overline {u}}{A_1-\overline {u}},&\quad \Theta _{A_2}&=\frac {1}{\hat \gamma }\ln \frac {\underline {T}-\overline {u}}{A_2-\overline {u}}, \\ \Theta _{M_1}&=\Theta _1+ \frac {1}{\hat \gamma }\ln \frac {\overline {T}-\underline {u}}{M_1-\underline {u}},&\quad \Theta _{M_2}&=\Theta _1+ \frac {1}{\hat \gamma } \ln \frac {\overline {T}-\underline {u}}{M_2-\underline {u}}, \end {aligned}$$

and the inequality $T_0<M_1$ has been taken into account.

Figures 3 and 4 schematically depict the graphs of the functions $x_3^{\Theta }(t)$ and $\varphi (t)$ for $t\in [0,\Theta ]$.

Fig. 3.

Graph of the function $x_3^{\Theta }(t)$.

Fig. 4.

Graph of the function $\varphi (t)$ .

It follows from the preceding that system (16) is actually a linear time-varying system of the form

$$ \dot x(t)=A(t)x(t)+f(t),$$

(18)

where $x=(x_1,x_2)^{\mathrm {T}}$ and

$$ A(t)=\begin {pmatrix} 0 & 1\\ -\dfrac {k}{m}-\dfrac {\alpha }{lm}\varphi (t) & -\dfrac {\beta }{m} \end {pmatrix},\quad f(t)=\begin {pmatrix} 0\\ \dfrac {\alpha }{lm}\Delta \varphi (t)-g \end {pmatrix}, $$

(19)

the matrix $A(t)$ and the column vector $f(t)$ being continuous $\Theta$-periodic functions; i.e., in particular, $A(t+\Theta )=A(t)$ and $f(t+\Theta )=f(t)$ for each $t\geq 0$.

It is well known [5, p. 215] that if the linear homogeneous $\Theta$-periodic system

$$ \dot x(t)=A(t)x(t)$$

(20)

does not have a nontrivial $\Theta$-periodic solution, then the corresponding inhomogeneous system (18) has a unique $\Theta$-periodic solution. Now note that if the homogeneous system (20) is asymptotically stable, then it cannot have a nontrivial $\Theta$-periodic solution.

Let us obtain conditions under which the linear homogeneous system (20) is asymptotically stable. To this end, we use the method proposed in [5, p. 197]. Consider system (20) with coefficient matrix $A(t)$ given by (19). This system is equivalent to the second-order differential equation

$$ \ddot y(t)+a\dot y(t)+b(t)y(t)=0, $$

(21)

where $y(t)=x_1(t)$, $\dot y(t)=x_2(t)$, and

$$ a=\frac {\beta }{m},\quad b(t)=\frac {\alpha }{l m}\varphi (t)+\frac {k}{m}. $$

Let us make the standard change of dependent variable $y=e^{-a t/2} z$ in Eq. (21); then

$$ \dot y=\biggl (\dot z-\frac {a}{2} z\biggr ) e^{-a t/2}\quad \text {and}\quad \ddot y=\biggl (\ddot z-a\dot z+\frac {a^2}{4} z\biggr ) e^{-a t/2}.$$

Therefore, this change of variable reduces Eq. (21) to the form

$$ \ddot z(t)+p(t)z(t)=0,$$

(22)

where

$$ p(t)=\frac {\alpha }{l m}\varphi (t)+\frac {k}{m}-\frac {\beta ^2}{4m^2}. $$

According to the results in the monograph [5, p. 202], if the $\Theta$-periodic function $p(t)$ satisfies the inequalities

$$ p(t)\geq 0,\quad 0<\Theta \int _0^\Theta p(t) \thinspace dt\leq 4,$$

then all solutions $z(t)$ of Eq. (22) are bounded together with their first derivatives. However, the boundedness of $z(t)$ and $\dot z(t)$ implies that the solutions $y(t)$ of Eq. (21), together with their derivatives $\dot y(t)$, tend to zero, and consequently, system (20) is asymptotically stable. Since $E_1\!\leq \!\varphi (t)\!\leq \!E_2$, we obtain a sufficient condition for system (20) with coefficient matrix $A(t)$ given by (19) to be asymptotically stable in the form

$$ \dfrac {\alpha }{l m} E_1+\dfrac {k}{m}-\dfrac {\beta ^2}{4m^2}>0, \quad \dfrac {\alpha }{l m} E_2+\dfrac {k}{m}-\dfrac {\beta ^2}{4m^2}\leq \dfrac {4}{\Theta ^2}.$$

(23)

Consequently, the linear inhomogeneous system (18) has a unique $\Theta$-periodic solution under condition (23). We denote this solution by $x^{\Theta }(t)=(x^{\Theta }_1(t), x^{\Theta }_2(t))^{\mathrm {T}}$.

Thus, we have proved the following assertion.

Theorem 1.

Let the parameters $\overline {u}$, $\underline {u}$, $\Theta _1$, and $\Theta$ of the programmed control (9) for system (4) satisfy the following conditions:

• 1. One has the inequalities

  $$ \begin {aligned} M_1&<\underline {T}=\frac {\underline {u}(1-e^{-\gamma (\Theta -\Theta _1)/\alpha })+ \overline {u}(1-e^{-\gamma \Theta _1/\alpha })e^{-\gamma (\Theta -\Theta _1)/\alpha } }{1-e^{-\gamma \Theta /\alpha }}, \\ A_2&>\overline {T}=\frac { \overline {u}(1-e^{-\gamma \Theta _1/\alpha })+ \underline {u}(1-e^{-\gamma (\Theta -\Theta _1)/\alpha })e^{-\gamma \Theta _1/\alpha } }{1-e^{-\gamma \Theta /\alpha }}. \end {aligned}$$

• 2. Condition (23) holds.

Then there exists a unique periodic motion $x^{\Theta }(t)=(x_1^{\Theta }(t),x_2^{\Theta }(t), x_3^{\Theta }(t))^{\mathrm {T}}$ in system (4) with the programmed control (9). Furthermore, $x_3^{\Theta }(0)=\underline {T}$.

3. PERIODIC MODE IN THE SYSTEM WITH A FEEDBACK

Let us return to the original problem (see Sec. 2) of constructing a feedback control (3) ensuring the existence of a periodic mode in the closed-loop system (5). The main idea for solving this problem is to choose the parameters of the feedback (3) based on the results in the paper [1] guaranteeing the existence of an oscillatory mode in the closed-loop system (5) and also based on the programmed control (9) calculated in accordance with Theorem 1 and the periodic solution $x^{\Theta }(t)$ produced by this control.

Thus, the following assertion holds based on Theorem 1 and sufficient conditions obtained in [1] for the existence of oscillatory modes.

Theorem 2.

Assume that

• 1. The parameters of system (4) satisfy the inequality

  $$ \Delta -\frac {mg+k\Delta }{k+\alpha E_1/l}>0.$$

• 2. The spectrum of each of the matrices

  $$ \begin {pmatrix} 0 & 1\\ -\dfrac {kl+\alpha E_1}{m} & - \dfrac {\beta }{m}\end {pmatrix},\quad \begin {pmatrix} 0 & 1\\ -\dfrac {kl+\alpha E_2}{m} &-\dfrac {\beta }{m}\end {pmatrix} $$

  lies on the negative half-axis and is simple.

• 3. The parameters $\overline {u}$ , $\underline {u}$ , $\Theta _1$ , and $\Theta$ satisfy the conditions in Theorem 1 and, in addition,

  $$ \underline {u}<M_1,\quad \overline {u}>A_2. $$

• 4. The numbers $y_1=x_1^{\Theta }(0)$ and $y_2=x_1^{\Theta }(\Theta _1)$ satisfy the inequalities

  $$ y_1>\Delta -\frac {mg+k\Delta }{k+\alpha E_1/l},\quad y_2<\Delta -\frac {mg+ k\Delta }{k+\alpha E_2/l}, $$

  where $x^{\Theta }(t)=(x_1^{\Theta }(t), x_2^{\Theta }(t), x_3^{\Theta }(t))^{\mathrm {T}}$ is the periodic solution of system (4) supplemented by the programmed control (9) with parameters $\overline {u}$, $\underline {u}$, $\Theta _1$, and $\Theta$.

• 5. The following inequalities hold for system (4) supplemented by the feedback (3) with parameters $\overline {u}$, $\underline {u}$, $y_1$, and $y_2$:

  $$ \frac {E_2}{E_1}-\frac {\beta C_3^2}{\bar t_1^*}<1,\quad \biggl (\frac {m^2g^2}{k}+\frac {\alpha E_2}{l}\Delta ^2\biggr )\nu _0<k\biggl (\Delta +\frac {mg}{k}\biggr )^{\!2},$$

  where

  $$ \begin {gathered} \bar t_1^*=\min \bigg \{\frac {1}{C_2\sqrt {2m}}, (y_2-y_1){\sqrt {\frac {E_1 m}{2 E_2 C_1}}}\bigg \}, \\ C_1=k\biggl (y_1+\frac {m g}{k}\biggr )^{\!2}+ \frac {\alpha }{l}E_2(y_1-\Delta )^2,\quad C_2=\frac {E_2}{mE_1}\biggl (\frac {\beta }{\sqrt {m}}+\sqrt {k}+ \sqrt {\frac {\alpha }{l} E_2}\biggr ), \\ C_3=\sqrt {\frac {E_1}{E_2(k+\alpha E_2/{l})}},\quad \nu _0=\max \{{H_{\max }}/{H_0}, 2\},\quad H_0=\frac {4mg\Delta E_1}{k+E_1}, \\ H_{\max }=\biggl (\frac {E_2}{E_1}\biggr )^{\!2}\bar H^*,\quad \bar H^*=\max \{H^*,\bar H\},\quad \bar H=\max \bigg \{\frac {m^2g^2}k+\frac {\alpha }l E_2\Delta ^2, k\biggl (\Delta +\frac {mg}k\biggr )^{\!2}\bigg \}, \\ H^*=\max \bigg \{\biggl (\frac {2\beta C_3 C_4 /\bar t_1^*}{1-E_2/E_1}+\beta C_3^2/\bar t_1^*\biggr )^{\!2},\frac {C_4^2}{C_3^2}\bigg \},\quad C_4=\frac {m g}{k}+\Delta +y_1; \end {gathered} $$

• 6. The conditions

  $$ 0<x_1^{\Theta }(t_0)<\zeta _{+},\quad x_2^{\Theta }(t_0)=0,\quad t_0<\Theta _{A_2}, $$

  are satisfied at time $t_0$ , where $\zeta _{+}$ is the positive root of the quadratic trinomial

  $$ p(\zeta )\equiv k\nu _0\biggl (\zeta +\frac {mg}k\biggr )^{\!2}+\frac {\alpha \nu _0 E_2}{l}(\zeta -\Delta )^2-k\biggl (\Delta +\frac {mg}k\biggr )^{\!2}.$$

Then the solution $\tilde x(t)$ of the closed-loop system (5) with the initial conditions

$$ \tilde x_1(0)=x_1^{\Theta }(t_0),\quad \tilde x_2(0)=x_2^{\Theta }(t_0),\quad \tilde x_3(0)=x_3^{\Theta }(t_0) $$

(24)

is an oscillatory mode with the parameters $t_1^*$, $t_2^*$, $y_1$, and $y_2$, where

$$ t_1^*=(y_2-y_1)\sqrt {m/H_{\max }}. $$

(An algorithm for calculating the constant $t_2^*$ is rather awkward; it is presented in full in [1].) Further, the solution $\tilde x(t)$ satisfies the identity $\tilde x(t)\equiv x^{\Theta }(t+t_0)$ for $t\in [0,t_1^*]$.

Now let us show that, under certain additional conditions on the constant $t_1^*$, the oscillatory mode $\tilde x(t)$ of system (5) with the initial conditions (24) is actually a periodic mode. To this end, it suffices to establish that if the parameters $\overline {u}$, $\underline {u}$, $y_1$, and $y_2$ of the bang-bang feedback control (3) satisfy the assumptions of Theorem 2, then, under the initial conditions (24), the control switches occur on the interval $[0,\Theta ]$ at $t_1=\Theta _1-t_0$ and $t_2=\Theta -t_0$.

Thus, let the assumptions of Theorem 2 be satisfied, and let the inequality

$$ \Theta _{A_2}-t_0<t_1^*\leq \Theta _1-t_0 $$

(25)

hold for $t_1^*$. Since the solution $\tilde x(t)$ of the closed-loop system (5) with the initial conditions (24) is oscillatory, we have the inequality

$$ \tilde x_1(t)<y_2,\quad t\in [0,\Theta _{A_2}-t_0]. $$

(26)

It follows by Theorem 2 that the identity $\tilde x(t)\equiv x^{\Theta }(t+t_0)$ holds for $t\in [0,\Theta _{A_2}-t_0]$.

Further, consider the behavior of the functions $\tilde x_1(t)$ and $\tilde x_2(t)$ on the interval $[\Theta _{A_2}-t_0,\Theta _1-t_0]$. First, note that, by the definition of the feedback (3), the identities $\tilde x_1(t)\equiv x_1^{\Theta }(t+t_0)$ and $\tilde x_2(t)\equiv x_2^{\Theta }(t+t_0)$ remain valid on the interval $[\Theta _{A_2}-t_0,\Theta _1-t_0]$ until time $t_*\in [\Theta _{A_2}-t_0,\Theta _1-t_0]$ such that $\tilde x_1(t_*)=x_1^{\Theta }(t_*+t_0)=y_2$. Let us show that $x_1^{\Theta }(t+t_0)\ne y_2$ for $t\in [\Theta _{A_2}-t_0,\Theta _1-t_0)$. Since $\varphi (t+t_0)\equiv E_2$ on the interval $[\Theta _{A_2}-t_0,\Theta _1-t_0]$, it follows that the functions $x_1^{\Theta }(t+t_0)$ and $x_2^{\Theta }(t+t_0)$ identically coincide on this interval with the respective components $\hat x_1(t)$ and $\hat x_2(t)$ of the solution $\hat x(t)$ of the linear time-invariant system

$$ \begin {array}{l} \dot x_1(t)=x_2(t),\\[2ex] \dot x_2(t)=-\biggl (\dfrac {k}{m}+\dfrac {\alpha }{lm}E_2\biggr )x_1(t)- \dfrac {\beta }{m}x_2(t)-g+\dfrac {\alpha }{lm}\Delta E_2 \end {array} $$

(27)

with the initial conditions

$$ x_1(\Theta _{A_2}-t_0)=x_1^{\Theta }(\Theta _{A_2}),\quad x_2(\Theta _{A_2}-t_0)=x_2^{\Theta }(\Theta _{A_2}). $$

(28)

By condition 2 in Theorem 2, the coefficient matrix of system (27) is stable and has simple spectrum. Let us show that the solution $\hat x(t)$ of this system with the initial conditions (28) satisfies the relation $\hat x_1(t)\ne y_2$ for $t\in [\Theta _{A_2}-t_0,\Theta _1-t_0)$.

Indeed, the first component $x_1(t)$ of each solution $x(t)$ of system (27) has the property

$$ x_1(t) \to x^*_1>y_2\quad \text {as}\quad t\to +\infty , $$

(29)

where $x^*_1=\Delta -(mg+k\Delta )/(k+\alpha E_2/l)$; the convergence in (29) was proved in [1], while the inequality in (29) is the second inequality in condition 4 in Theorem 2.

Consider the equation

$$ \hat x_1(t)=y_2,\quad t\geq \Theta _{A_2}-t_0. $$

(30)

Since the vector function $(\hat x_1(t),\hat x_2(t))^{\mathrm {T}}$ on the interval $[\Theta _{A_2}-t_0,\Theta _1-t_0]$ is a solution of system (27) whose coefficient matrix has negative distinct eigenvalues $\lambda _1$ and $\lambda _2$, we have the representation

$$ \hat x_1(t)=C_1 e^{\lambda _1t}+C_2 e^{\lambda _2t}+x^*_1,$$

where $C_1$ and $C_2$ are some constants, which are not zero simultaneously, because

$$ \hat x_1(\Theta _{A_2}-t_0)<y_2<x^*_1. $$

Therefore, Eq. (30) can be written in the form

$$ C_1 e^{\lambda _1t}+C_2 e^{\lambda _2t}=y_2-x^*_1,\quad \text {where}\quad \lambda _1<0,\quad \lambda _2<0,\quad C_1^2+C_2^2>0,\quad t>\Theta _{A_2}. $$

Note that the function on the left-hand side in this equation may have at most one point of extremum for $t>0$, and hence Eq. (30) may have at most one root by virtue of property (29). Consequently, the equation $x_1^{\Theta }(t+t_0)=y_2$ may have at most one root on the interval $t\in [\Theta _{A_2}-t_0,\Theta _1-t_0]$. Since the function $x_1^{\Theta }(t+t_0)$ takes the value $y_2$ at the point $t=\Theta _1-t_0$ by a condition in Theorem 2, we conclude that $x_1^{\Theta }(t+t_0)\ne y_2$ for $t\in {[\Theta _{A_2}-t_0,\Theta _1-t_0)}$. Thus,

$$ \begin {array}{c} \tilde x_1(t)\ne y_2,\quad t\in [\Theta _{A_2}-t_0,\Theta _1-t_0),\quad \text {and}\quad \tilde x_1(\Theta _1-t_0)=y_2. \end {array}$$

(31)

Now assume that the condition

$$ \Theta _{M_1}-\Theta _1<t_1^*\leq \Theta _2 $$

(32)

is additionally satisfied for $t_1^*$. Since the solution $\tilde x(t)$ of the closed-loop system (5) with the initial conditions (24) is an oscillatory mode, we have the inequality $\tilde x_1(t)>y_1,\quad t\in [\Theta _1-t_0,\Theta _{M_1}-t_0].$ It follows in view of relations (31) and (26) that

$$ \tilde x(t)\equiv x^{\Theta }(t+t_0)\quad \text {for}\quad t\in [0,\Theta _{M_1}-t_0].$$

(33)

Now consider the behavior of the functions $\tilde x_1(t)$ and $\tilde x_2(t)$ on the interval $[\Theta _{M_1}-t_0,\Theta -t_0]$. By analogy with the preceding argument, note that the identities $\tilde x_1(t)\equiv x_1^{\Theta }(t+t_0)$ and $\tilde x_2(t)\equiv x_2^{\Theta }(t+t_0)$ remain valid on the interval $[\Theta _{M_1}-t_0,\Theta -t_0]$ until time $t_*\in [\Theta _{M_1}-t_0,\Theta -t_0]$ such that $\tilde x_1(t_*)=x_1^{\Theta }(t_*+t_0)=y_1$. Let us show that $x_1^{\Theta }(t+t_0)\ne y_1$ for $t\in [\Theta _{M_1}-t_0,\Theta -t_0)$. Since $\varphi (t+t_0)\equiv E_1$ on the interval $[\Theta _{M_1}-t_0,\Theta -t_0]$, it follows that the functions $x_1^{\Theta }(t+t_0)$ and $x_2^{\Theta }(t+t_0)$ identically coincide on this interval with the respective components $\hat x_1(t)$ and $\hat x_2(t)$ of the solution $\hat x(t)$ of the linear time-invariant system

$$ \begin {array}{l} \dot x_1(t)=x_2(t),\\[2ex] \dot x_2(t)=-\biggl (\dfrac {k}{m}+\dfrac {\alpha }{lm}E_1\biggr )x_1(t) -\dfrac {\beta }{m}x_2(t)-g+\dfrac {\alpha }{lm}\Delta E_1 \end {array} $$

(34)

with the initial conditions

$$ x_1(\Theta _{M_1}-t_0)=x_1^{\Theta }(\Theta _{M_1}),\quad x_2(\Theta _{M_1}-t_0)=x_2^{\Theta }(\Theta _{M_1}). $$

(35)

By condition 2 in Theorem 2, the coefficient matrix of system (34) is stable and has simple spectrum. Let us show that the solution $\hat x(t)$ of this system with the initial conditions (35) satisfies the relation $\hat x_1(t)\ne y_1$ for $t\in [\Theta _{M_1}-t_0,\Theta -t_0)$.

Indeed, the first component $x_1(t)$ of each solution $x(t)$ of system (34) has the property

$$ x_1(t) \to x^{{**}}_1<y_1\quad \text {as}\quad t \to \infty ,$$

(36)

where $x^{**}=\Delta -(mg+k\Delta )/(k+\alpha E_1/l)$; the convergence in (36) was proved in the paper [1], while the inequality is the first inequality in condition 4 in Theorem 2.

Consider the equation

$$ \hat x_1(t)=y_1,\quad t\geq \Theta _{M_1}-t_0. $$

(37)

Since the vector function $(x_1^{\Theta }(t),x_2^{\Theta }(t))^{\mathrm {T}}$ on the interval $[\Theta _{M_1}-t_0,\Theta -t_0]$ is a solution of system (34) whose coefficient matrix has distinct negative eigenvalues $\lambda ^{\prime }_1$ and $\lambda ^{\prime }_2$, one has the representation

$$ \hat x_1(t)=C_1 e^{\lambda ^{\prime }_1t}+C_2 e^{\lambda ^{\prime }_2t}+x^{{**}}_1, $$

where $C_1$ and $C_2$ are some constants, which are not zero simultaneously, because

$$ \hat x_1(\Theta _{M_1}-t_0)>y_1>x^{{**}}_1.$$

Therefore, Eq. (37) can be written in the form

$$ C_1 e^{\lambda ^{\prime }_1t}+C_2 e^{\lambda ^{\prime }_2t}=y_1-x^{{**}}_1,\quad \text {where}\quad \lambda ^{\prime }_1<0,\quad \lambda ^{\prime }_2<0,\quad C_1^2+C_2^2>0,\quad t\geq \Theta _{M_1}-t_0.$$

Note that the function on the left-hand side in this equation may have at most one point of extremum for $t>0$, and then Eq. (37) may have at most one root by virtue of property (36). Consequently, the equation $x_1^{\Theta }(t+t_0)=y_1$ may have at most one root on the interval $t\in [\Theta _{M_1}-t_0,\Theta -t_0]$. Since the function $x_1^{\Theta }(t+t_0)$ takes the value $y_1$ at the point $t=\Theta -t_0$ by a condition in Theorem 2, we conclude that $x_1^{\Theta }(t+t_0)\ne y_1$ for $t\in [\Theta _{M_1}-t_0,\Theta -t_0)$. Thus,

$$ \begin {array}{c} \tilde x_1(t)\ne y_1,\quad t\in [\Theta _{M_1}-t_0,\Theta -t_0),\quad \text {and}\quad \tilde x_1(\Theta -t_0)=y_1. \end {array}$$

This, together with identity (33), implies that

$$ \tilde x(t)\equiv x^{\Theta }(t+t_0)\quad \text {for}\quad t\in [0,\Theta -t_0].$$

(38)

Let us impose one more constraint on the constant $t_1^*$; namely, let

$$ t_1^*>t_0.$$

(39)

Since the solution $\tilde x(t)$ of the closed-loop system (5) with the initial conditions (24) is an oscillatory mode, it follows that

$$ \tilde x_1(t)<y_2,\quad t\in [\Theta -t_0,\Theta ]. $$

(40)

This, together with identity (38), implies that the switching times of the bang-bang control (3) and the programmed control (9) for $t\in [0,\Theta ]$ coincide. Then one has the identity $\tilde x(t)\equiv x^{\Theta }(t+t_0)$ on this interval, and this identity remains valid for all $t\geq 0$ by virtue of the $\Theta$-periodicity of the function $x^{\Theta }(t+t_0)$.

Consequently, the oscillatory mode $\tilde x(t)$ of system (5) with the initial conditions (24) is a periodic mode. Thus, we have proved the following assertion about the existence of a periodic mode in the closed-loop system (5).

Theorem 3.

Let the assumptions of Theorem 2 be satisfied, and let inequalities (25), (32), and (39) hold. Then there exists a periodic mode with the initial conditions (24) in the closed-loop system (5).

4. SIMULATION RESULTS

Consider system (1) with the parameters

$$ \begin {gathered} m=0.018,\quad \beta =0.7,\quad k=0.07,\quad \alpha =1.32\cdot 10^{-8},\quad l=0.2,\quad \Delta =0.009,\quad \gamma =1.76\cdot 10^9, \\ M_1=24.3,\quad M_2=52.7,\quad A_1=32.8,\quad A_2=57.5,\quad E_1=3\cdot 10^8,\quad E_2=8\cdot 10^8. \end {gathered}$$

Using the results in the present paper, we can calculate the parameters

$$ \overline {u}=80,\quad \underline {u}=1,\quad y_1=0.00172,\quad y_2=0.0063 $$

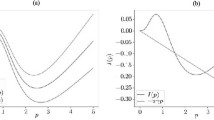
of the feedback (3) for which there exists a periodic motion (Fig. 5) with period $\Theta =0.2$ in the corresponding closed-loop system with $E(0)=4.73\cdot 10^8$ and with the initial conditions

$$ y(0)=0.0032,\quad \dot y(0)=0,\quad T(0)=41.067. $$

Here the bang-bang control switching times are $t_1=\Theta _1-t_0$ and $t_2=\Theta -t_0$, where $\Theta _1=0.1$ and $t_0=0.036$.

Fig. 5.

Graphs of the functions $y(t)$, $T(t)$, and $E(t)$ corresponding to a periodic mode of system (1).

CONCLUSIONS

The paper considers a mathematical model of a thermal energy harvester [1] in the form of the controlled nonlinear dynamical system (1) whose coefficients are positive numerical parameters. The main problem is to choose a control algorithm ensuring the occurrence of a periodic motion in the closed-loop system. As a control algorithm, it is proposed to use output feedback with feedback operator in the form of a bang-bang hysteresis control. As a result, sufficient conditions are obtained for the coefficients and initial values of the state variables of system (1) and for the parameters of the controller (3) ensuring the occurrence of a periodic mode in the closed-loop system.