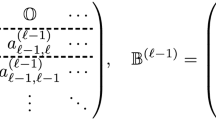Skip to main content
SpringerLink
Log in

On Stable Runge–Kutta Methods for Solving Hyperbolic Equations by the Discontinuous Galerkin Method

  • NUMERICAL METHODS
  • Published:
Differential Equations Aims and scope Submit manuscript

Abstract

We consider Runge–Kutta methods whose stability domain includes a disk of maximum diameter for given number of stages and order. These methods are used to solve initial value problems obtained by approximating hyperbolic systems with the use of the discontinuous Galerkin method. Two three-stage methods in the class in question are proposed for which, using test problems for the transport equation and for the system of gasdynamic equations, we study the possibility to maintain the stability and monotonicity of the numerical solution with the maximum possible time steps.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.

Similar content being viewed by others

REFERENCES

  1. Kulikovskii, A.G., Pogorelov, N.V., and Semenov, A.Yu., Matematicheskie voprosy chislennogo resheniya giperbolicheskikh sistem uravnenii (Mathematical Issues of Numerically Solving Hyperbolic Systems of Equations), Moscow: Fizmatlit, 2001.

    Google Scholar 

  2. Samarskii, A.A. and Popov, Yu.P., Raznostnye metody resheniya zadach gazovoi dinamiki (Difference Methods for Solving Gas Dynamics Problems), Moscow: Nauka, 1992.

    Google Scholar 

  3. Cockburn, B. and Shu, C.-W., TVB Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws. II. General framework, Math. Comput., 1989, vol. 52, no. 186, pp. 411–435.

    MathSciNet  MATH  Google Scholar 

  4. Cockburn, B. and Shu, C.-W., Runge–Kutta discontinuous Galerkin methods for convection-dominated problems, J. Sci. Comput., 2001, vol. 16, pp. 2440–2463.

    Article  MathSciNet  Google Scholar 

  5. Galepova, V.D., Lukin, V.V., Marchevskii, I.K., and Fufaev, I.N., Comparative study of limiters of WENO and Hermite WENO families for computing one-dimensional gas flows by the RKDG method, Preprint of Keldysh Inst. Appl. Math., Moscow, 2017, no. 131.

  6. Dolejsi, V., May, G., and Rangarajan, A., A continuous hp-mesh model for adaptive discontinuous Galerkin schemes, Appl. Numer. Math., 2018, vol. 124, pp. 1–21.

    Article  MathSciNet  Google Scholar 

  7. Klein, B., Müller, B., Kummer, F., and Oberlack, M., A high-order discontinuous Galerkin solver for low-Mach number flows, Int. J. Numer. Methods Fluids, 2015, vol. 81, pp. 489–520.

    Article  MathSciNet  Google Scholar 

  8. Galanin, M.P., Lukin, V.V., and Chechetkin, V.M., 3D hydrodynamical simulation of accretion disk in binary star system using RKDG CFD solver, J. Phys. Conf. Ser., 2018, vol. 1103, p. 012019.

    Article  Google Scholar 

  9. Galanin, M.P., Savenkov, E.B., and Tokareva, S.A., Solving gas dynamics problems with shock waves using the Runge-Kutta discontinuous Galerkin method, Math. Models Comput. Simul., 2009, vol. 1, no. 5, pp. 635–645.

    Article  MathSciNet  Google Scholar 

  10. Shu, C.-W. and Osher., S., Efficient implementation of essentially non-oscillatory shock capturing schemes, J. Comput. Phys., 1988, vol. 77, pp. 439–471.

    Article  MathSciNet  Google Scholar 

  11. Gottlieb, S., Ketcheson, D., and Shu, C.-W., High order strong stability preserving time discretizations, J. Sci. Comput., 2009, vol. 38, pp. 251–289.

    Article  MathSciNet  Google Scholar 

  12. Toulorge, T. and Desmet, W., Optimal Runge–Kutta schemes for discontinuous Galerkin space discretizations applied to wave propagation problems, J. Comput. Phys., 2011, vol. 231, pp. 2067–2091.

    Article  MathSciNet  Google Scholar 

  13. Jeltsch, R. and Torrilhon, M., Flexible stability domains for explicit Runge–Kutta methods, in Some Topics in Industrial and Applied Mathematics, Jeltsch, R., Li, D., and Sloan, I.H., Eds., Beijing, 2007.

  14. Ladonkina, M.E., Neklyudova, O.A., Ostapenko, V.V., and Tishkin, V.F., Studying the accuracy of the discontinuous Galerkin method when calculating solutions with shock waves, Preprint of Keldysh Inst. Appl. Math., Moscow, 2018, no. 195.

  15. Hairer, E. and Wanner, G., Solving Ordinary Differential Equations II. Stiff and Differential-Algebraic Problems, Berlin: Springer, 1996. Translated under the title: Reshenie obyknovennykh differentsial’nykh uravnenii. Zhestkie i differentsial’no-algebraicheskie zadachi, Moscow: Mir, 1999.

    MATH  Google Scholar 

  16. Hairer, E., Nørsett, S.P., and Wanner, G., Solving Ordinary Differential Equations I. Nonstiff Problems, Berlin: Springer, 1987. Translated under the title: Reshenie obyknovennykh differentsial’nykh uravnenii. Nezhestkie zadachi, Moscow: Mir, 1990.

  17. Godunov, S.K., A difference method for numerical calculation of discontinuous solutions to equations of hydrodynamics, Mat. Sb., 1959, vol. 47, no. 3, pp. 271–306.

    MathSciNet  MATH  Google Scholar 

  18. Zhong, X. and Shu, C.-W., A simple weighted essentially nonoscillatory limiter for Runge–Kutta discontinuous Galerkin methods, J. Comput. Phys., 2013, vol. 232, pp. 397–415.

    Article  MathSciNet  Google Scholar 

  19. Zhu, J., Zhong, X., Shu, C.-W., and Qiu, J.-X., Runge–Kutta discontinuous Galerkin method with a simple and compact Hermite WENO limiter, Commun. Comput. Phys., 2016, vol. 19, pp. 944–969.

    Article  MathSciNet  Google Scholar 

  20. Korchagova, V.N., Sautkina, S.M., Lukin, V.V., and Fufaev, I.N., Experimental evaluation of the efficiency of parallelization of the RKDG method for solving two-dimensional gasdynamic problems, XIV mezhdunar. konf. “Parallel’nye vychislitel’nye tekhnologii” (PaVT–2020). Korotkie stat’i i opisaniya plakatov (Parallel Comput. Technol. (PCT) 2020. Short Articles and Poster Descriptions) (Perm, March 31–April 2, 2020), Chelyabinsk, 2020, pp. 142–151.

  21. Giuliani, A. and Krivodonova, L., Analysis of slope limiters on unstructured triangular meshes, J. Comput. Phys., 2018, vol. 374, pp. 1–26.

    Article  MathSciNet  Google Scholar 

Download references

Funding

The research by V.V. Lukin was financially supported by the Russian Science Foundation, project no. 17-79-20445.

Author information

Authors and Affiliations

  1. Keldysh Institute of Applied Mathematics, Moscow, 125047, Russia

    V. V. Lukin

  2. Ivannikov Institute for System Programming of the Russian Academy of Sciences, Moscow, 109004, Russia

    V. V. Lukin, V. N. Korchagova & S. M. Sautkina

  3. Bauman Moscow State Technical University, Moscow, 105005, Russia

    V. V. Lukin & S. M. Sautkina

Authors
  1. V. V. Lukin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. N. Korchagova
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. M. Sautkina
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to V. V. Lukin, V. N. Korchagova or S. M. Sautkina.

Additional information

Translated by V. Potapchouck

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lukin, V.V., Korchagova, V.N. & Sautkina, S.M. On Stable Runge–Kutta Methods for Solving Hyperbolic Equations by the Discontinuous Galerkin Method. Diff Equat 57, 921–933 (2021). https://doi.org/10.1134/S0012266121070089

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0012266121070089

Search

Navigation