INTRODUCTION

Stabilization towards the Sun is an important mode employed on the majority of spacecraft. Stabilization accuracy requirements are relatively low in this case. Few degrees discrepancy of solar panels attitude relative to the Sun direction provides sufficient illumination conditions for batteries charge. Magnetorquers are well suited for this purpose. Their inherent inferior performance compared to the reaction wheel does not make significant difference. At the same time the attitude control system power consumption is reduced, reaction wheels lifetime saved and saturation avoided. Prominent magnetic control system drawback is the restriction on the control torque direction. Although the satellite is generally controllable [1, 2], this restriction is hard to accommodate in practice. However, in the case of uniaxial orientation to the Sun, rotational stabilization [3] can be used, which has been used together with the magnetic system since the launch of the Tiros-II satellite in 1960. In this case, the own dynamic properties of the satellite complement the capabilities of the control system.

Three main attitude tasks—spin rate control, wobble suppression, and spin axis reorientation—are fully controllable by magnetorquers [4, 5], although simplified approaches for the control construction for each channel are also viable [6–8]. The approach that does not require separation of control modes is based on calculating the difference between the current and required angular momenta of the satellite [9], which can be used in case of failure of some of the magnetic coils [10]. Separately we should mention the special algorithms that take into account the specifics of the information received from the orientation sensors. For example, in [11], the readings of the solar sensor and magnetometer are used to stabilize the satellite in a sun-synchronous orbit. In [12], the difference in the current collection of solar panels is used, and in [13], the direction to the Sun. The derivative of this direction is used in Sdot control [14–16] which is inspired by the Bdot law. Another modification of this basic control law is suggested in [17].

Present paper investigates the satellite dynamics under the action of Prisma satellite control law [18]. Evolutionary equations [19] are averaged [20, 21] to facilitate stability analysis for a satellite moving on a Sun-synchronous orbit. Maximum moment of inertia stabilization is verified to be stable. However, inclined attitude of the rotation axis relative to the Sun direction turned out be stable under certain conditions on the satellite inertia relations and control parameters. Likewise, specific conditions are established for the stabilization of the minimum moment of inertia axis in the required direction. Numerical simulation examples are provided for these situations.

1 EQUATIONS OF MOTION

Axisymmetric satellite moving on a circular orbit is considered below. The satellite is subjected to the control torque only.

Evolutionary Equations

Let us introduce a reference frame associated with the center of the Earth, the third axis of which is directed to the Sun. This system will be considered inertial on time intervals of a few hours. In the study of its motion, the OZ1Z2Z3 orientation of the satellite is described with respect to this refrerence frame. Since only the uniaxial orientation of the satellite is of interest, the direction of the first and second axes can be chosen arbitrarily.

Satellite motion is described by the evolutionary equations organized in two groups. The first group includes the angular momentum vector magnitude \(L\) and its attitude angles \(\rho \) and \(\sigma \) that describe the momentum vector motion in the \(OZ\) frame (Fig. 1). Reference frame \(O{{L}_{1}}{{L}_{2}}{{L}_{3}}\) related to the angular momentum of the satellite is introduced. Its third axis is aligned with the momentum vector. The \(O{{L}_{2}}\) axis is defined by the rotation \(\dot {\sigma }\) around the \(O{{Z}_{3}}\) axis. The \(O{{L}_{1}}\) axis is derived after the rotation \(\dot {\rho }\) around \(O{{L}_{2}}\) axis (Fig. 1).

Fig. 1.
figure 1

Angular momentum attitude in the inertial space.

Full size image

Second group of variables describes the satellite attitude relative to the angular momentum reference frame. Satellite-fixed frame \(O{{x}_{1}}{{x}_{2}}{{x}_{3}}\) is introduced using the principal central axes of inertia of the satellite. Its attitude relative to the \(O{{L}_{1}}{{L}_{2}}{{L}_{3}}\) frame is represented by the Euler angles \(\psi \), \(\theta \), \(\varphi \) (rotations sequence 3-1-3).

The transition matrices \(OL\) → \(OZ\) and \(Ox\) → \(OL\) are correspondingly

$${\mathbf{Q}} = \left( {\begin{array}{*{20}{c}} {\cos \rho \cos \sigma }&{ - \sin \sigma }&{\sin \rho \cos \sigma } \\ {\cos \rho \sin \sigma }&{\cos \sigma }&{\sin \rho \sin \sigma } \\ { - \sin \rho }&0&{\cos \rho } \end{array}} \right),$$
(1)
$${\mathbf{A}} = \left( {\begin{array}{*{20}{c}} {\cos \varphi \cos \psi - \cos \theta \sin \varphi \sin \psi }&{ - \sin \varphi \cos \psi - \cos \theta \cos \varphi \sin \psi }&{\sin \theta \sin \psi } \\ {\cos \varphi \sin \psi + \cos \theta \sin \varphi \cos \psi }&{ - \sin \varphi \sin \psi + \cos \theta \cos \varphi \cos \psi }&{ - \sin \theta \cos \psi } \\ {\sin \theta \sin \varphi }&{\sin \theta \cos \varphi }&{\cos \theta } \end{array}} \right).$$
(2)

Evolutionary equations of the satellite with symmetric inertia tensor \({\mathbf{J}} = {\text{diag}}(A,A,C)\) are

$$\left. \begin{gathered} \frac{{dL}}{{dt}} = {{M}_{{3L}}},\,\,\,\,\frac{{d\rho }}{{dt}} = \frac{1}{L}{{M}_{{1L}}},\,\,\,\,\frac{{d\sigma }}{{dt}} = \frac{1}{{L\sin \rho }}{{M}_{{2L}}}, \\ \frac{{d\theta }}{{dt}} = \frac{1}{L}\left( {{{M}_{{2L}}}\cos \psi - {{M}_{{1L}}}\sin \psi } \right), \\ \frac{{d\varphi }}{{dt}} = L\cos \theta \left( {\frac{1}{C} - \frac{1}{A}} \right) \\ + \,\,\frac{1}{{L\sin \theta }}\left( {{{M}_{{1L}}}\cos \psi + {{M}_{{2L}}}\sin \psi } \right), \\ \frac{{d\psi }}{{dt}} = \frac{L}{A} - \frac{1}{L}{{M}_{{1L}}}\cos \psi {\text{cot}}\theta \\ - \,\,\frac{1}{L}{{M}_{{2L}}}\left( {\cot \rho + \sin \psi \cot \theta } \right), \\ \end{gathered} \right\}$$
(3)

where the control torque components \({{M}_{{kL}}}\) are defined in the \(OL\) frame. Only three variables are relevant for the stabilization analysis. The angular momentum magnitude represents the rotation rate of a spinning satellite. Angle \(\rho \) defines the discrepancy between the angular momentum vector (the \(O{{L}_{3}}\) axis) and the Sun direction (the \(O{{Z}_{3}}\) axis). Nutation angle \(\theta \) defines the deviation of the axis of symmetry \({{{\mathbf{e}}}_{3}}\) from the angular momentum vector. This axis should be stabilized towards the Sun in the following analysis. Averaging technique is applied to remove irrelevant variables in the equations of motion [22].

Attitude Control Algorithm

The control torque acting on the satellite is

$${\mathbf{M}} = {\mathbf{m}} \times {\mathbf{B}},$$

where the control dipole moment \({\mathbf{m}}\) and the geomagnetic induction vector \({\mathbf{B}}\) should be defined to obtain complete expressions for the equations (3).

The control dipole moment suggested in [18] for the Prisma satellite is used. This control utilizes the difference between the current satellite angular velocity \({\boldsymbol{\mathbf{\omega }}}\) and the required one \({{{\boldsymbol{\mathbf{\omega }}}}_{{ref}}}\) given by the expression

$${{{\boldsymbol{\mathbf{\omega }}}}_{{ref}}} = {{\omega }_{0}}\left( {\mu {{{\mathbf{S}}}_{x}} + {{{\mathbf{e}}}_{3}}} \right).$$

The first term in \({{{\boldsymbol{\mathbf{\omega }}}}_{{ref}}}\) drives the angular velocity vector towards the Sun direction in the satellite reference frame \({{{\mathbf{S}}}_{x}}\). Second term ensures that the rotation occurs around \({{{\mathbf{e}}}_{3}}\) axis. Parameter \(\mu \) defines relative contribution of two terms. Parameter \({{\omega }_{0}}\) influences the resulting rotation rate which is anticipated to settle at \({{\omega }_{0}}\left( {1 + \mu } \right)\). The control dipole moment is

$${\mathbf{m}} = k\left( {{\boldsymbol{\mathbf{\omega }}} - {{{\boldsymbol{\mathbf{\omega }}}}_{{ref}}}} \right) \times {\mathbf{b}},$$
(4)

where \({\mathbf{b}}\) is a unit geomagnetic induction vector, \(k\) is a control gain.

Geomagnetic Field Model

Geomagnetic field representation requires reference frame associated with the Earth. Frame \(O{{X}_{1}}{{X}_{2}}{{X}_{3}}\) is introduced for this purpose. Its first axis is directed to the ascending node of the satellite orbit, third axis is aligned with the Earth rotation axis. This reference frame will be used for the numerical simulation of the satellite motion.

Geomagnetic field is represented in the \(O{{Y}_{1}}{{Y}_{2}}{{Y}_{3}}\) frame which results in a rotation of \(O{{X}_{1}}{{X}_{2}}{{X}_{3}}\) around \(O{{X}_{2}}\) axis by the angle \(\Theta \). This angles is defined as

$$\tan \Theta = \frac{{3\sin 2i}}{{2\left( {1 - 3{{{\sin }}^{2}}i + \sqrt {1 + 3{{{\sin }}^{2}}i} } \right)}},$$

where \(i\) is the orbit inclination. The induction vector moves uniformly in the \(OY\) frame and circumscribes a cone during one orbit revolution. The expression for the induction vector is [24, 25]:

$${{{\mathbf{B}}}_{Y}} = {{B}_{0}}\left( {\begin{array}{*{20}{c}} {\sin \Theta \sin 2u} \\ {\sin \Theta \cos 2u} \\ {\cos \Theta } \end{array}} \right),$$
(5)

where \(u = {{\omega }_{{orb}}}t + u(0)\) is the argument of latitude, \({{\omega }_{{orb}}}\) is constant orbital rate, and \({{B}_{0}}\) is the induction vector magnitude. This simple model is used in the averaged equations of motion, whereas numerical simulation utilizes IGRF model [25].

2 EVOLUTIONARY EQUATIONS STABILITY

To apply the averaging method, it is necessary to separate the variables into fast and slow varying. In the absence of a control torque, the angular momentum in the inertial space is conserved, which is expressed in the constancy of its magnitude and orientation angles in equations (3). The nutation angle θ also remains constant. The satellite undergoes a regular precession, in which the angles γ and υ change rapidly. When the control system is acted upon, the constants in the unperturbed motion begin to change. If the control value is sufficiently small, these variables can be considered slow and equations (3) can be averaged over the fast variables and time.

To formalize the concept of slow variation, the equations of motion should be written in a dimensionless form. For this purpose, we use the orbital period as a measure of time in equations (3) and, accordingly, the argument of latitude is used instead of time; we refer the angular momentum to its unperturbed value L = L0l and introduce a small parameter that characterizes the variation of the angular momentum over one orbital revolution ε = kB0/ω0C. The dimensionless equations are written as follows:

$$\left. \begin{gathered} \frac{{dl}}{{du}} = \varepsilon l{{{\bar {M}}}_{{3L}}},\,\,\,\,\frac{{d\rho }}{{du}} = \varepsilon {{{\bar {M}}}_{{1L}}},\,\,\,\,\frac{{d\sigma }}{{du}} = \frac{\varepsilon }{{\sin \rho }}{{{\bar {M}}}_{{2L}}}, \\ \frac{{d\varphi }}{{du}} = {{\eta }_{1}}l\cos \theta + \frac{\varepsilon }{{\sin \theta }}\left( {{{{\bar {M}}}_{{1L}}}\cos \psi + {{{\bar {M}}}_{{2L}}}\sin \psi } \right), \\ \frac{{d\psi }}{{du}} = {{\eta }_{2}}l - \varepsilon {{{\bar {M}}}_{{1L}}}\cos \psi \cot \theta \\ - \,\,\varepsilon {{{\bar {M}}}_{{2L}}}\left( {\cot \rho + \sin \psi \cot \theta } \right), \\ \frac{{d\theta }}{{du}} = \varepsilon \left( {{{{\bar {M}}}_{{2L}}}\cos \psi - {{{\bar {M}}}_{{1L}}}\sin \psi } \right), \\ \end{gathered} \right\}$$
(6)

where \({{\eta }_{1}} = \frac{{{{L}_{0}}}}{{{{\omega }_{{orb}}}}}\left( {\frac{1}{C} - \frac{1}{A}} \right)\), \({{\eta }_{2}} = \frac{{{{L}_{0}}}}{{A{{\omega }_{{orb}}}}}\), dimensionless control torque components are \({{\bar {M}}_{{kL}}}\). Parameters \({{\eta }_{k}}\) are large compared to \(\varepsilon \).

Control torque expression is required for further analysis. The torque in the satellite frame is

$${{{\mathbf{M}}}_{x}} = k{{B}_{0}}\left\{ {\left( {{{{\boldsymbol{\mathbf{\omega }}}}_{x}} - \mu {{\omega }_{0}}{{{\mathbf{S}}}_{x}} - {{\omega }_{0}}{{{\mathbf{e}}}_{3}}} \right) \times {{{\mathbf{b}}}_{x}}} \right\} \times {{{\mathbf{b}}}_{x}}.$$

Dimensionless induction vector is introduced as \({\mathbf{B}} = {{B}_{0}}{\mathbf{b}}\). This is a unit vector in the simplified geomagnetic model. Equations (6) operate with the control torque expression in the \(OL\) frame,

$$\begin{gathered} {{{\mathbf{M}}}_{L}} = \frac{{k{{B}_{0}}L}}{C}\left\{ {\left( {\frac{C}{L}{{{\boldsymbol{\mathbf{\omega }}}}_{L}} - \mu \frac{{{{L}_{{ref}}}}}{L}{{{\mathbf{Q}}}^{T}}\left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ 1 \end{array}} \right)} \right.} \right. \\ - \,\,\left. {\left. {\frac{{{{L}_{{ref}}}}}{L}{\mathbf{A}}\left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ 1 \end{array}} \right)} \right) \times {{{\mathbf{Q}}}^{T}}{{{\mathbf{b}}}_{Z}}} \right\} \times {{{\mathbf{Q}}}^{T}}{{{\mathbf{b}}}_{Z}}, \\ \end{gathered} $$
(7)

where \({{L}_{{ref}}} = C{{\omega }_{0}}\). The angular velocity vector in the \(OL\) frame is derived from the angular momentum as \({\mathbf{J}}{{{\boldsymbol{\mathbf{\omega }}}}_{x}} = {{{\mathbf{L}}}_{x}}\). Drawing upon the momentum expression in the \(OL\) frame \({{{\mathbf{L}}}_{L}} = \left( {0,0,L} \right)\) and utilizing the transition matrix \({\mathbf{A}}\), the velocity is expressed as

$${{{\boldsymbol{\mathbf{\omega }}}}_{L}} = \frac{L}{C}\left( {\begin{array}{*{20}{c}} {\frac{C}{A}{{a}_{{11}}}{{a}_{{31}}} + \frac{C}{A}{{a}_{{12}}}{{a}_{{32}}} + {{a}_{{13}}}{{a}_{{33}}}} \\ {\frac{C}{A}{{a}_{{21}}}{{a}_{{31}}} + \frac{C}{A}{{a}_{{22}}}{{a}_{{32}}} + {{a}_{{23}}}{{a}_{{33}}}} \\ {\frac{C}{A}{{a}_{{31}}}{{a}_{{31}}} + \frac{C}{A}{{a}_{{32}}}{{a}_{{32}}} + {{a}_{{33}}}{{a}_{{33}}}} \end{array}} \right).$$
(8)

Evolutionary equations describe the angular momentum motion and the nutation angle variation after equations (7)–(8) are averaged over the fast variables \(\varphi \), \(\psi \), and \(u\). However, the induction vector \({{{\mathbf{b}}}_{Z}}\left( u \right)\) is not yet defined. This vector is derived in the \(OY\) frame whereas the satellite motion is described in the \(OZ\) frame. Averaging over \(\psi \) and designating the induction vector components in the \(OL\) frame as \({{b}_{k}}\), without averaging over \(u\), the equations of motion become

$$\left. \begin{gathered} \frac{1}{{\varepsilon l}}\dot {l} = - \left( {b_{1}^{2} + b_{2}^{2}} \right)\left( {{{{\cos }}^{2}}\theta + \frac{C}{A}{{{\sin }}^{2}}\theta } \right) + \mu \frac{{{{l}_{{ref}}}}}{l}\left\{ {{{b}_{1}}{{b}_{3}}\sin \rho + \left( {b_{1}^{2} + b_{2}^{2}} \right)\cos \rho } \right\} + \frac{{{{l}_{{ref}}}}}{l}\left( {b_{1}^{2} + b_{2}^{2}} \right)\cos \theta , \\ \frac{1}{\varepsilon }\dot {\rho } = {{b}_{1}}{{b}_{3}}\left( {{{{\cos }}^{2}}\theta + \frac{C}{A}{{{\sin }}^{2}}\theta } \right) - \mu \frac{{{{l}_{{ref}}}}}{l}\left\{ {{{b}_{1}}{{b}_{3}}\cos \rho + \left( {b_{2}^{2} + b_{3}^{2}} \right)\sin \rho } \right\} - \frac{{{{l}_{{ref}}}}}{l}{{b}_{1}}{{b}_{3}}\cos \theta , \\ \frac{1}{\varepsilon }\sin \rho \dot {\sigma } = {{b}_{2}}{{b}_{3}}\left( {{{{\cos }}^{2}}\theta + \frac{C}{A}{{{\sin }}^{2}}\theta } \right) + \mu \frac{{{{l}_{{ref}}}}}{l}\left\{ {{{b}_{1}}{{b}_{2}}\sin \rho - {{b}_{2}}{{b}_{3}}\cos \rho } \right\} - \frac{{{{l}_{{ref}}}}}{l}{{b}_{2}}{{b}_{3}}\cos \theta . \\ \end{gathered} \right\}$$
(9)

Notations are retained for the averaged variables. Parameter \({{l}_{{ref}}} = {{{{L}_{{ref}}}} \mathord{\left/ {\vphantom {{{{L}_{{ref}}}} {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}}\) defines the goal angular momentum magnitude.

Motion on a Sun-Synchronous Orbit

Further analysis requires specific expressions for the components of the induction vector. For this purpose, it is necessary to determine the transition matrix from the OY to the OZ frame. Recall that the third axis in the OZ frame is oriented to the Sun, while the other two axes are chosen arbitrarily. The OY frame, on the other hand, is uniquely defined. To obtain the transition between OY and OZ, we set the orientation of the direction vector to the Sun in the OY frame. For this purpose, we can apply the same approach as in determining the orientation of the angular momentum vector in inertial space and introducing the OL frame. Specifically, setting the orientation of the direction to the Sun in the OY frame by the angles ρS and σS as shown in Fig. 1, we set the transition matrix QS between the OY and OZ frame in the same way as in expression (1).

The induction vector components in the \(OZ\) frame \({{b}_{{kZ}}} = \sum\nolimits_{n = 1}^3 {q_{{nk}}^{S}{{b}_{{nY}}}} \) contain constant elements of the transition matrix \({{{\mathbf{Q}}}^{S}}\) or, alternatively, trigonometric functions of constant angles \({{\rho }^{S}}\), \({{\sigma }^{S}}\). This makes resulting averaged equations cumbersome and unsuitable for the stability analysis. Compact equations may be obtained for the dawn-dusk Sun-synchronous orbit. Geomagnetic induction vector components (5) are simplified for \(\sin \Theta \approx 1\), \(\cos \Theta \approx 0\) since \(\Theta \approx i \approx {{90}^{ \circ }}\). Next, axes \(OY\) and \(OZ\) almost coincide. Indeed, the Sun direction \(OZ\) is almost perpendicular to the orbital plane on a dawn-dusk orbit. Likewise, \(OY\) is directed perpendicular to the orbit plane if \(\Theta = i = {{90}^{ \circ }}\) and almost perpendicular for a near polar orbit.

Finally, assuming that reference frames \(OY\) and \(OZ\) coincide and \(\sin \Theta \approx 1\), \(\cos \Theta \approx 0\), the induction vector is expressed in the \(OZ\) frame as \({{{\mathbf{b}}}_{Z}} = \left( {\sin 2u,\cos 2u,0} \right)\). Adopting the transformation \({{{\mathbf{b}}}_{L}} = {{{\mathbf{Q}}}^{T}}{{{\mathbf{b}}}_{Z}}\) and averaging (9) over the argument of latitude final evolutionary equations are obtained

$$\left. \begin{gathered} \frac{1}{{\varepsilon l}}\dot {l} = - \frac{1}{2}\left( {1 + {{{\cos }}^{2}}\rho } \right)\left( {{{{\cos }}^{2}}\theta + \frac{C}{A}{{{\sin }}^{2}}\theta } \right) \\ + \,\,\mu \frac{{{{l}_{{ref}}}}}{l}\cos \rho + \frac{1}{2}\frac{{{{l}_{{ref}}}}}{l}\left( {1 + {{{\cos }}^{2}}\rho } \right)\cos \theta , \\ \frac{1}{\varepsilon }\dot {\rho } = \left\{ {\frac{1}{2}\cos \rho \left( {{{{\cos }}^{2}}\theta + \frac{C}{A}{{{\sin }}^{2}}\theta } \right)} \right. \\ - \,\,\left. {\mu \frac{{{{l}_{{ref}}}}}{l} - \frac{1}{2}\frac{{{{l}_{{ref}}}}}{l}\cos \rho \cos \theta } \right\}\sin \rho , \\ \frac{1}{\varepsilon }\dot {\theta } = \frac{1}{2}\left( {\frac{{A - C}}{A}\cos \theta - \frac{{{{l}_{{ref}}}}}{l}} \right)\left( {1 + \frac{1}{2}{{{\sin }}^{2}}\rho } \right)\sin \theta . \\ \end{gathered} \right\}$$
(10)

Stability Analysis

Evolutionary equations (10) are relatively compact and admit stability analysis. Clearly, the equilibrium positions are \(\sin \rho = 0\) and \(\sin \theta = 0\). However, some inclined equilibrium configurations exist for \(\rho \) and \(\theta \). Second and third equations in (10) define the corresponding equilibria. The first equation defines the equilibrium angular momentum magnitude. It depends on the equilibrium for \(\rho \) and \(\theta \). All cases are analyzed below.

1. \(\theta = 0\), \(\rho = 0\) (required motion)

This equilibrium corresponds to the required attitude, with the angles between the Sun direction, angular momentum, and \({{{\mathbf{e}}}_{3}}\) axis all equal to zero. Substituting zero angles to the first equation in (10) yields the equation for the rotation rate equilibrium calculation,

$$\frac{1}{{\varepsilon l}}\dot {l} = - 1 + \mu \frac{{{{l}_{{ref}}}}}{l} + \frac{{{{l}_{{ref}}}}}{l}.$$

Therefore, the satellite should rotate with the angular momentum magnitude \(l = \left( {1 + \mu } \right){{l}_{{ref}}}\). This expression is substituted into the second and third equations in (10). Linearization around equilibrium position provides

$$\frac{1}{\varepsilon }\dot {\rho } = - \frac{1}{2}\frac{\mu }{{1 + \mu }}\rho ,\,\,\,\,\frac{1}{\varepsilon }\dot {\theta } = - \frac{1}{2}\left( {\frac{{C - A}}{A} + \frac{1}{{\mu + 1}}} \right)\theta .$$

The equilibrium is stable if \(C > A\). The required rotation around the maximum moment of inertia is stable. Stability of the rotation around the minimum moment of inertia is ensured if

$$\frac{{C - A}}{A} + \frac{1}{{\mu + 1}} > 0 \to C > A\frac{\mu }{{1 + \mu }}.$$
(11)

For example \(\mu = 1\) leads to the condition \(C > {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}A\), while \(\mu = 2\) leads to \(C > {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}A\). Generally, stabilization of the axis of the minimum moment of inertia is possible if its relation to the maximum one is not too small. Allowed difference between the minimum and maximum moments increases as parameter \(\mu \) decreases.

2. Equilibrium \(\theta = 0\), \(\rho = \pi \) (\({{{\mathbf{e}}}_{3}}\) is directed out of the Sun).

The angular momentum magnitude equilibrium value is \(l = \left( {1 - \mu } \right){{l}_{{ref}}}\), so \(\mu < 1\) is required in this case. Linearized second equation in (10) is

$$\frac{1}{\varepsilon }\dot {\rho } = \frac{1}{2}\frac{\mu }{{1 - \mu }}\rho .$$

Taking into account \(\mu < 1\) the equilibrium is identified as unstable.

3. Equilibrium \(\theta = \pi \), \(\rho = 0\) (\({{{\mathbf{e}}}_{3}}\) is directed out of the Sun).

The equilibrium angular momentum is \(l = \left( { - 1 + \mu } \right){{l}_{{ref}}}\), so \(\mu > 1\). Linearized equations for the angles are

$$\frac{1}{\varepsilon }\dot {\rho } = - \frac{1}{2}\frac{\mu }{{ - 1 + \mu }}\rho ,\,\,\,\,\frac{1}{\varepsilon }\dot {\theta } = - \frac{1}{2}\left( {\frac{{C - A}}{A} - \frac{1}{{\mu - 1}}} \right)\theta .$$

Second equation establishes the stability condition

$$C > A\frac{\mu }{{ - 1 + \mu }}.$$

For example \(\mu = 2\) leads to \(C > 2A\) which is not feasible due to the inertia tensor properties. Parameter \(\mu = 3\) leads to \(C > 1.5A\). The satellite should have specific mass distribution and relatively high control parameter \(\mu \) for the stabilization opposite to the Sun direction.

Three collinear equilibrium configurations stability is summarized as follows. Control parameter \(\mu \) should be constrained to 1–2, so Case 3 stability is avoided. Rotation should be performed around the maximum moment of inertia axis. If rotation around the minimum inertia axis is necessary, the moment of inertia should not be considerably smaller than the maximum one.

4. Consider an inclined equilibrium arising from the third equation in (10)

$$\frac{{A - C}}{A}\cos \theta - \frac{{{{l}_{{ref}}}}}{l} = 0.$$
(12)

Inclined configuration for \(\rho \) can be derived from the second equation in (10). However, they are stable only if \(\mu = 0\). Together with results of Cases 1–3 this indicates that always \(\rho = 0\), so the angular momentum vector is always directed towards the Sun. The satellite axis \({{{\mathbf{e}}}_{3}}\) on the contrary may exhibit unacceptable stable behavior.

Expression (12) is introduced to the first equation (10) along with \(\rho = 0\) to find the equilibrium condition

$$ - \left( {{{{\cos }}^{2}}\theta + \frac{C}{A}{{{\sin }}^{2}}\theta } \right)\frac{A}{{A - C}}\frac{1}{{\cos \theta }} + \mu + \cos \theta = 0,$$

which leads to

$$\cos \theta = \frac{1}{\mu }\frac{C}{{A - C}}.$$
(13)

The angular momentum equilibrium magnitude is \(l = {{\mu A{{l}_{{ref}}}} \mathord{\left/ {\vphantom {{\mu A{{l}_{{ref}}}} C}} \right. \kern-0em} C}\). Unlike Cases 1 and 2 the angular momentum vector is not aligned with \({{{\mathbf{e}}}_{3}}\) axis. Its component along \({{{\mathbf{e}}}_{3}}\) axis is

$${{l}_{3}} = {{\mu A{{l}_{{ref}}}\cos \theta } \mathord{\left/ {\vphantom {{\mu A{{l}_{{ref}}}\cos \theta } C}} \right. \kern-0em} C} = \frac{A}{{A - C}}{{l}_{{ref}}}.$$
(14)

The equilibrium position \(\rho = 0\) is stable if

$$ - 1 < \frac{1}{\mu }\frac{C}{{A - C}} < 1.$$
(15)

In case \(C > A\) this is expanded into

$$C > \frac{\mu }{{\mu + 1}}A\,\,{\text{and}}\,\,C > \frac{\mu }{{\mu - 1}}A.$$

These relations are not satisfied if \(\mu \in \left[ {1,2} \right]\) due to the inertia tensor properties. Therefore, this interval for \(\mu \) is preferable, which repeats Cases 1–3 conclusion. It eliminates both stabilization opposite to the Sun direction and inclined equilibrium.

In case \(C < A\) stability condition (15) leads to

$$A > \frac{{\mu - 1}}{\mu }C\,\,{\text{and}}\,\,A > \frac{{\mu + 1}}{\mu }C.$$
(16)

For example \(\mu = 1\) provides \(A > 2C\), parameter \(\mu = 2\) provides \(A > 1.5C\). Let us demonstrate the stability of the position of equality (13) under conditions (16) in order to make sure that the satellite reaches an oblique position. Linearizing the third equation in (10) near the equilibrium position \({{\theta }_{0}}\), \(\theta = {{\theta }_{0}} + \alpha \), we obtain

$$\begin{gathered} \frac{1}{\varepsilon }\dot {\theta } = \frac{1}{2}\left( {\lambda \left\{ {\cos {{\theta }_{0}} - \sin {{\theta }_{0}}\alpha } \right\} - \frac{1}{\mu }\frac{C}{A}} \right) \\ \times \,\,\left\{ {\sin {{\theta }_{0}} + \cos {{\theta }_{0}}\alpha } \right\}. \\ \end{gathered} $$

Here \(\lambda = \frac{{A - C}}{A} = \frac{1}{{\cos {{\theta }_{0}}}}\frac{1}{\mu }\frac{C}{A}\). The equation reduces to

$$\frac{1}{\varepsilon }\dot {\theta } = - \frac{1}{2}\frac{1}{\mu }\frac{C}{A}\cos {{\theta }_{0}}{{\tan }^{2}}{{\theta }_{0}}\alpha .$$

Stability is observed if \(\cos {{\theta }_{0}} > 0\) which means \(\frac{1}{\mu }\frac{C}{{A - C}} > 0\). This condition is satisfied if \(A > \frac{{\mu + 1}}{\mu }C\) according to (16). Therefore, (16) ensures stability for \(\rho \) and \(\theta \).

Comparison of conditions (16) and (11) reveals the border values of parameters that define stability of either the required stabilization of the minimum moment of inertia axis, or stability of the inclined configuration.

Stability analysis is summarized below.

— Parameter \(\mu \) should lie between 1 and 2.

— It is preferable to stabilize the maximum moment of inertia axis.

— Stabilization of the minimum moment of inertia axis is possible if \(C > A\frac{\mu }{{1 + \mu }}\). Namely, this relation is satisfied if \(C > {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}A\) and \(\mu \in \left[ {1,2} \right]\).

Alternatively, if \(\mu = 1\) and \(C < {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}A\) the satellite stabilizes in the inclined position.

3 NUMERICAL EXAMPLES

Numerical simulation is performed with various disturbances. Following satellite and environment parameters and assumptions are adopted:

— Orbit inclination 97°, altitude 550 km, eccentricity 0.01, right ascension of ascending node 90°;

— Sun direction in the \(OY\) frame is defined by angles \({{\rho }^{S}}\) = 80° and \({{\sigma }^{S}}\) = 10°. Therefore, the Sun direction is close to the \(O{{Y}_{1}}\) axis. Likewise, the orbit normal is close to \(O{{Y}_{1}}\) with chosen orbit inclination and right ascension;

— Control gain \(k\) = 600 N m s/T, reference rotation rate \({{\omega }_{0}}\) = 0.5 °/s.

— Aerodynamic torque is calculated as a sum of torques acting on the sides of a satellite:

satellite is a cube with 30 cm sides;

center of mass displacement relative to the center of pressure is 2, 3, and 4 cm along the satellite reference frame axes;

atmosphere density is 1.8 × 10–13 kg/m3 (average solar activity);

— Residual dipole moment 2 × 10–2 A m2 has constant and normally distributed components;

— Sun direction estimation accuracy is 1°, angular velocity estimation accuracy is 10–4 s–1 (constant and normally distributed noise);

— Unknown disturbance sources are modelled as a constant and periodic torque with overall value approximately two times less than the gravitational torque value.

Figure 2 provides a numerical simulation example for the satellite with inertia moments 1.0, 0.8, 1.3 kg m2, parameter \(\mu \) = 1. Rotation occurs around the maximum moment of inertia which together with μ = 1 ensures stability of the required attitude.

Fig. 2.
figure 2

Stabilization in the required direction.

Full size image

Angular velocity components are designated \({{\Omega }_{k}}\) in Fig. 2. Figure 3 presents an example of stabilization in the opposite direction. Inertia moments of the satellite are 1.0, 0.8, 1.6 kg m2, parameter \(\mu \)=3. Therefore, Case 2 conditions are satisfied (\(C > 1.5A\) and \(\mu = 3\)).

Fig. 3.
figure 3

Stabilization in the opposite direction.

Full size image

Note that the initial data are chosen in such a way that the satellite is initially close to stabilization in the opposite direction. The same initial data can be seen in Fig. 2, where, however, the satellite has stabilized in the required direction.

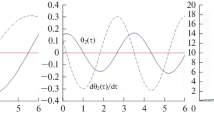
Finally Fig. 4 presents an example of inclined stabilization with inertia moments 1.0, 0.8, 0.3 kg m2 and parameter \(\mu \) = 1.

Fig. 4.
figure 4

Stabilization in the inclined position.

Full size image

The satellite should settle at the rotation inclined by the angle \(\theta \approx 60\)° relative to the Sun direction and angular momentum vector according to (13). Rotation around \({{{\mathbf{e}}}_{3}}\) axis should occur with approximately 0.75 °/s rate according to (14). Since inertia moments \(A\) and \(B\) are different, their average value 0.9 kg m2 may be used in expressions (13) and (14) for the inertia moment \(A\).

CONCLUSIONS

Magnetically actuated satellite single axis stabilization towards the Sun is considered. The control builds upon the current satellite velocity, Sun direction in the satellite reference frame, and the required rotation rate. Averaged evolutionary equations of motion are utilized to identify satellite equilibrium positions. Apart from obvious positions of the satellite stabilizing along the Sun direction, both in the required and opposite directions, an inclined attitude is derived. Analysis reveals the satellite inertia and control parameters that ensure different equilibrium stability. Stabilization of the maximum moment of inertia axis towards the Sun is always possible. Conditions for the stabilization of the minimum moment of inertia axis are derived. Requirements for the inertia moments and control parameter are found that ensure avoidance of the unwanted equilibria stability. Numerical simulation examples are provided for different stabilization cases with various disturbance sources.