Periodic Approximation of the Rotational Motion of the Photon-12 Satellite

Abstract

The results of repeated processing of magnetic measurements carried out on the Photon-12 satellite (which was in orbit from September 9 to 24, 1999) are described. The processing was performed in order to reconstruct the uncontrolled rotational motion of this satellite. In re-processing, the simplified mathematical model of rotational motion was used. The actual orbit of a satellite (the apogee height is 380 km, the perigee height is 220 km) is replaced by a circular orbit; the expression for the aerodynamic moment acting on a satellite is simplified. The system of differential equations underlying the new model is autonomous and proved to be sufficiently accurate to reconstruct the satellite motion based on magnetic measurements in the case in which the satellite angular velocity was not very low and grew gradually. In the last third of the flight, when the satellite motion became virtually stable and had a sufficiently high angular velocity, this system could be reduced to a generalized-conservative system. Such a reduction makes more definite the set of its solutions suitable for approximate description of the actual motion of a satellite. In some segments of motion, the combining of which covers about 3 days, it was possible to use, for this purpose, the periodic solutions continued from the Lyapunov periodic solutions.

INTRODUCTION

This paper is a continuation of works [1, 2]. In paper [1], the magnetic measurements carried out in 1999 on the Photon-12 satellite were reprocessed. The original processing was done soon after the flight [3] using the detailed model of rotational motion of this satellite. The model adopted in [1] is simpler than the model of [3], but is comparable with that model in accuracy when reconstructing the motion with a not very low angular velocity. The model of [1] allowed reconstructing the evolution of the actual motion of Photon-12 with growing angular velocity. An even simpler model is used below in which the satellite’s actual orbit (the apogee height is 380 km, the perigee height is 220 km) is replaced by a circular orbit. This replacement made it possible to describe the rotational motion of a satellite by autonomous differential equations, which, in the case of steady-state motion with a sufficiently high angular velocity (the result of the evolution indicated above), could be reduced to a generalized-conservative system. Such a reduction made it possible to approximately, but fairly accurately, describe the actual motion of a satellite over time spans up to 3.5 h by periodic solutions extrapolated from Lyapunov’s periodic solutions. Periodic solutions suitable for this purpose were studied in [2]. Their similarity to the virtually rotational motion of Photon-12 was also noted there. However, this similarity has not been investigated in detail. Such an investigation is performed below.

EQUATIONS OF A SATELLITE ROTATIONAL MOTION

We consider the satellite to be an axisymmetric solid body, the center of masses of which moves over an unchanged circular orbit. To write down the equations of satellite motion, we introduce four right-hand Cartesian coordinate systems.

The $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ system is formed by the major central axes of inertia of a satellite. Point $O$ is satellite ’s center of masses, and the $O{{x}_{1}}$ axis is the axis of material symmetry of a satellite. This axis is close to the longitudinal axis of a satellite and is directed from the lander to the instrumental module. The satellite’s moment of inertia relative to the $O{{x}_{1}}$ axis is denoted by ${{I}_{1}},$ the equal moments of inertia relative to the $O{{x}_{2}}$ and $O{{x}_{3}}$ axes are denoted by ${{I}_{2}}.$

The auxiliary coordinate system $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ serves for writing the equations of a satellite rotational motion. The $O{{y}_{1}}$ axis coincides with the $O{{x}_{1}}$ axis; the $O{{x}_{2}}$ and $O{{x}_{3}}$ axes are obtained from the $O{{y}_{2}}$ and $O{{y}_{3}}$ axes by turning the $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ system at angle $\chi$ around the axis $O{{y}_{1}}.$ The kinematic bound between the $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ and $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ systems is specified by the condition that the projection of the absolute angular velocity of the second of them on the $O{{y}_{1}}$ axis is zero. The projections of this angular velocity on the $O{{y}_{2}}$ and $O{{y}_{3}}$ axes are denoted by ${{w}_{2}}$ and ${{w}_{3}}.$ Let absolute angular velocity ${\mathbf{\omega }}$ of a satellite in the system $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ have components $({{\omega }_{1}},{{\omega }_{2}},{{\omega }_{3}}).$ Then, $\dot {\chi } = {{\omega }_{1}}$ and

$$\begin{gathered} {{\omega }_{2}} = {{w}_{2}}\cos \chi + {{w}_{3}}\sin \chi , \\ {{\omega }_{3}} = - {{w}_{2}}\sin \chi + {{w}_{3}}\cos \chi . \\ \end{gathered} $$

(1)

Here and below, the dot indicates differentiation with respect to time t.

The measurement data of onboard magnetometers are interpreted in the instrumental coordinate system $O{{z}_{1}}{{z}_{2}}{{z}_{3}}$. This system can be transferred into the $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ system by two successive turns. The first turn is performed at angle ${{\alpha }_{c}}$ around the axis $O{{z}_{2}},$ while the second turn, at angle ${{\beta }_{c}}$, is performed around the axis $O{{z}_{3}},$ which took place after the first turn. In the general case, in order to specify the position of one coordinate system relative to another, three angles are needed. In this case, it could be possible to introduce another angle of turning the instrumental system around its axis $O{{z}_{1}},$ obtained after the first two turns. However, since the direction of one of axes $O{{x}_{2}}$ and $O{{x}_{3}}$ can be chosen arbitrarily, it is convenient to assume the third angle is equal to zero, thereby fixing the $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ system position relative to the system $O{{z}_{1}}{{z}_{2}}{{z}_{3}}.$ The matrix of transition between these coordinate systems is denoted as $\left\| {{{b}_{{ij}}}} \right\|_{{i,j = 1}}^{3},$ where ${{b}_{{ij}}}$ is the cosine of the angle between the axes $O{{z}_{i}}$ and $O{{x}_{j}}.$ The elements of this matrix are expressed in terms of angles ${{\alpha }_{c}}$ and ${{\beta }_{c}}$ by the formulas

$$\begin{array}{*{20}{c}} {{{b}_{{11}}} = \cos {{\alpha }_{c}}{\kern 1pt} \cos {{\beta }_{c}},}&{{{b}_{{12}}} = - \cos {{\alpha }_{c}}{\kern 1pt} \sin {{\beta }_{c}},}&{{{b}_{{13}}} = \sin {{\alpha }_{c}},} \\ {{{b}_{{21}}} = \sin {{\beta }_{c}},}&{{{b}_{{22}}} = \cos {{\beta }_{c}},}&{{{b}_{{23}}} = 0,} \\ {{{b}_{{31}}} = - \sin {{\alpha }_{c}}{\kern 1pt} \cos {{\beta }_{c}},}&{{{b}_{{32}}} = \sin {{\alpha }_{c}}{\kern 1pt} \sin {{\beta }_{c}},}&{{{b}_{{33}}} = \cos {{\alpha }_{c}}.} \end{array}$$

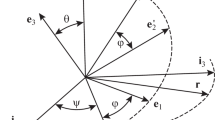
The rotational motion of a satellite is studied with respect to the orbital coordinate system $O{{X}_{1}}{{X}_{2}}{{X}_{3}}.$ Its axes $O{{X}_{1}}$ and $O{{X}_{3}}$ are directed along the geocentric velocity and radius vector of point $O$. The matrix of transition from the system $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ to the orbital system is denoted by $\left\| {{{a}_{{ij}}}} \right\|_{{i,j = 1}}^{3},$ where ${{a}_{{ij}}}$ is the cosine of the angle between the axes $O{{X}_{i}}$ and $O{{y}_{j}}.$ The elements of this matrix will be expressed as a function of angles $\psi ,$ $\theta$, and $\delta ,$ which will be introduced such that the $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ system is transferred into the $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ system by three successive turns: (1) at angle $\psi$ around the axis $O{{X}_{3}},$ (2) at angle $\theta$ around the new axis $O{{X}_{2}},$ and (3) at angle $\delta$ around the new axis $O{{X}_{1}},$ coinciding with the axis $O{{y}_{1}}.$ So, $\theta$ is the angle between the axis $O{{y}_{1}}$and the plane $O{{X}_{1}}{{X}_{2}},$ while $\psi$ is the angle between the projection of axis $O{{y}_{1}}$ on the plane $O{{X}_{1}}{{X}_{2}}$ and the axis $O{{X}_{1}}.$ These two angles specify the direction of the $O{{y}_{1}}$ axis in the orbital coordinate system. There exist the relationships

$$\begin{gathered} \begin{array}{*{20}{c}} {{{a}_{{11}}} = \cos \psi \cos \theta ,} \\ {{{a}_{{21}}} = \sin \psi \cos \theta ,} \\ {{{a}_{{31}}} = - \sin \theta ,} \end{array}\,\,\,\,\begin{array}{*{20}{c}} {{{a}_{{12}}} = \cos \psi \sin \theta \sin \delta - \sin \psi \cos \delta ,} \\ {{{a}_{{22}}} = \sin \psi \sin \theta \sin \delta + \cos \psi \cos \delta ,} \\ {{{a}_{{32}}} = \cos \theta \sin \delta ,} \end{array} \\ \begin{array}{*{20}{c}} {{{a}_{{13}}} = \cos \psi \sin \theta \cos \delta + \sin \psi \sin \delta ,} \\ {{{a}_{{23}}} = \sin \psi \sin \theta \cos \delta - \cos \psi \sin \delta ,} \\ {{{a}_{{33}}} = \cos \theta \cos \delta .} \end{array} \\ \end{gathered} $$

The system of equations of rotational motion of a satellite is formed by the dynamic Euler equations for angular velocities ${{w}_{2}}$ and ${{w}_{3}}$ and by the kinematic Poisson equations for the first and third rows of matrices $\left\| {{{a}_{{ij}}}} \right\|.$ In the Euler equations, the gravitational and restoring aerodynamic moments are taken into account, as well as the constant moment along the axis $O{{x}_{1}}.$ When calculating the aerodynamic moment, the atmosphere is to be considered motionless in absolute space; its density along the orbit is constant; the outer shell of a satellite is assumed to be a sphere with the center on the axis $O{{x}_{1}}.$ Under the assumptions that have been made, the aerodynamic moment is characterized by a single scalar parameter. The system of equations of rotational motion has the form [4, 5]

$$\begin{gathered} {{{\dot {w}}}_{2}} + \lambda {{\omega }_{1}}{{w}_{3}} = - 3\omega _{0}^{2}(1 - \lambda ){{a}_{{31}}}{{a}_{{23}}} + p{{a}_{{13}}}, \\ {{{\dot {w}}}_{3}} - \lambda {{\omega }_{1}}{{w}_{2}} = 3\omega _{0}^{2}(1 - \lambda ){{a}_{{31}}}{{a}_{{32}}} - p{{a}_{{12}}}, \\ {{{\dot {a}}}_{{11}}} + {{w}_{2}}{{a}_{{13}}} - {{w}_{3}}{{a}_{{12}}} = - {{\omega }_{0}}{{a}_{{31}}}, \\ {{{\dot {a}}}_{{12}}} + {{w}_{3}}{{a}_{{11}}} = - {{\omega }_{0}}{{a}_{{32}}},\,\,\,\,{{{\dot {a}}}_{{13}}} - {{w}_{2}}{{a}_{{11}}} = - {{\omega }_{0}}{{a}_{{33}}}, \\ {{{\dot {a}}}_{{31}}} + {{w}_{2}}{{a}_{{33}}} - {{w}_{3}}{{a}_{{32}}} = {{\omega }_{0}}{{a}_{{11}}}, \\ {{{\dot {a}}}_{{32}}} + {{w}_{3}}{{a}_{{31}}} = {{\omega }_{0}}{{a}_{{12}}},\,\,\,\,{{{\dot {a}}}_{{31}}} - {{w}_{2}}{{a}_{{31}}} = {{\omega }_{0}}{{a}_{{13}}}, \\ {{\omega }_{1}} = \Omega + \varepsilon (t - {{t}_{0}}),\,\,\,\,\lambda = \frac{{{{I}_{1}}}}{{{{I}_{2}}}}. \\ \end{gathered} $$

(2)

Here, ${{\omega }_{0}}$ is the orbital frequency,$p$ is the aerodynamic parameter, and $\Omega$ and $\varepsilon$ are constant quantities. In Eq. (2), the explicit form of the solution of one of the Euler equations ${{\dot {\omega }}_{1}} = \varepsilon$ is used with the initial condition ${{\omega }_{1}}({{t}_{0}}) = \Omega .$. The choice of ${{t}_{0}}$ will be indicated below.

In the numerical integration of Eqs. (2), the time measurement unit is 10³ s and the units of measurement of other quantities are $[{{\omega }_{i}}] = [{{w}_{i}}] = {{10}^{{ - 3}}}\,\,{{{\text{s}}}^{{ - 1}}},$ and $[\varepsilon ] = [p] = {{10}^{{ - 6}}}\,\,{{{\text{s}}}^{{ - 2}}}.$ Variables ${{a}_{{1i}}}$ and ${{a}_{{3i}}}$ are interdependent and are bound by the conditions of orthogonality of matrix $\left\| {{{a}_{{ij}}}} \right\|.$ For this reason, initial conditions ${{a}_{{1i}}}({{t}_{0}})$ and ${{a}_{{3i}}}({{t}_{0}})$ are expressed in terms of angles $\psi ,$ $\theta$, and $\delta .$ The elements of the second row of matrix $\left\| {{{a}_{{ij}}}} \right\|$ are calculated as the vector product of its third and first rows. Formulas (1) and the relation $\chi = \Omega (t - {{t}_{0}}) + {{\varepsilon {{{(t - {{t}_{0}})}}^{2}}} \mathord{\left/ {\vphantom {{\varepsilon {{{(t - {{t}_{0}})}}^{2}}} 2}} \right. \kern-0em} 2}$ allow us to find functions ${{\omega }_{2}}(t)$ and ${{\omega }_{3}}(t)$ and the motion of the system $O{{x}_{1}}{{x}_{2}}{{x}_{3}},$ by solving Eqs. (2).

Parameter $\lambda$ is known: $\lambda \approx 0.24.$ Nevertheless, this parameter and parameters $p$ and $\varepsilon$ are determined from the processing of measurement data, along with unknown initial conditions of satellite motion; i.e., they serve as matching parameters.

Equations (2) were derived from similar equations of rotational motion [1] by transferring to the circular orbit and using the orbital coordinate system as a system, with respect to which the satellite motion is considered. To compensate all performed simplifications, the satellite motions were reconstructed, in which the angular velocity component ${{\omega }_{1}}$ was sufficiently great. The processing of measurements with using equations (2) was carried out according to the scheme [1] and gave close results.

RECONSTRUCTION OF THE ROTATIONAL MOTION OF A SATELLITE BASED ON THE MAGNETIC MEASUREMENTS

Mirage instruments with several three-component magnetometers were installed onboard the Photon-12. Since the motion of a satellite was uncontrollable, the measurement data of these instruments and Eqs. (2) could be used to determine the actual rotational motion of a satellite using the conventional statistical techniques. The technique used below is as follows [1, 4]. Using measurements taken over a certain time span ${{t}_{0}} \leqslant t \leqslant {{t}_{0}} + T,$ we have constructed functions ${{\hat {h}}_{i}}(t),$ which specified, on this span, the components of the vector of the local magnetic-field strength in the coordinate system $O{{z}_{1}}{{z}_{2}}{{z}_{3}}.$ The root-mean-square approximation errors did not exceed 200$\gamma$ ($1\gamma = {{10}^{{ - 5}}}$ Oe). Then, the pseudomeasurements were calculated as $h_{i}^{{(n)}} = {{\hat {h}}_{i}}({{t}_{n}}),$ ${{t}_{n}} = {{t}_{0}} + {{nT} \mathord{\left/ {\vphantom {{nT} N}} \right. \kern-0em} N},$ where n = 0, 1, 2, …, N. Usually, $T = 100{\kern 1pt} - {\kern 1pt} 300$ min, ${T \mathord{\left/ {\vphantom {T N}} \right. \kern-0em} N} \approx 1$ min. Pseudomeasurements served as the initial information for finding solutions of Eqs. (2) describing the actual motion of a satellite.

In accordance with the least-squares method, the reconstruction of the actual motion of a satellite was considered to be the solution of Eqs. (2), which delivered a minimum to the functional

$$\begin{gathered} \Phi = \sum\limits_{i = 1}^3 {\left\{ {\sum\limits_{n = 0}^N {{{{\left[ {h_{i}^{{(n)}} - {{h}_{i}}({{t}_{n}})} \right]}}^{2}} - (N + 1)\Delta _{i}^{2}} } \right\}} , \\ {{\Delta }_{i}} = \frac{1}{{N + 1}}\sum\limits_{n = 0}^N {\left[ {h_{i}^{{(n)}} - {{h}_{i}}({{t}_{n}})} \right]} ,\,\,\,\,{{h}_{i}}(t) = \sum\limits_{j = 1}^3 {{{b}_{{ij}}}h_{j}^{^\circ }(t)} . \\ \end{gathered} $$

(3)

Here, ${{\Delta }_{i}}$ are the estimates of constant biases in pseudomeasurements,$h_{j}^{ \circ }(t)$ are the components of the Earth’s magnetic field (EMF) strength at point $O$ in the coordinate system $O{{x}_{1}}{{x}_{2}}{{x}_{3}},$ calculated using the IGRF2005 model.

To use Eqs. (2) for calculating functional (3), it is necessary to specify the bound of the $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ system with the Greenwich coordinate system, in which the actual satellite orbit is specified, and the EMF strength is calculated. For this purpose, the actual satellite orbit was approximated by a circular orbit on the span ${{t}_{0}} \leqslant t \leqslant {{t}_{0}} + T$. The approximation was constructed using the least-squares method on the basis of fairly accurate values of an actual phase vector of satellite’s center of masses specified on a uniform grid with a step of 3 min. The circular orbit was specified by five elements: radius, average motion (orbital frequency ${{\omega }_{0}}$), initial value of the latitude argument, and ascending node longitude and inclination. Along the circular orbit, the EMF strength components were calculated in the $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ coordinate system for moments ${{t}_{n}}.$ These components were used in the repeated calculation of functional (3) in the process of its minimization. Using the solution of Eqs. (2), these components were recalculated into the system $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ and then into the system $O{{x}_{1}}{{x}_{2}}{{x}_{3}}.$ The initial point of the processed data segment was always used as ${{t}_{0}}$ in Eqs. (2).

The acceptability of transition to a circular orbit, as well as the expected accuracy of approximating pseudomeasurements by the extremal of functional (3), were estimated by minimizing the function

$$\Psi = {{\sum\limits_{n = 0}^N {\left\{ {\sqrt {\sum\limits_{i = 1}^3 {{{{\left[ {\kappa h_{i}^{{(n)}} - \Delta _{i}^{'}} \right]}}^{2}}} } - \sqrt {\sum\limits_{i = 1}^3 {{{{[h_{i}^{ \circ }({{t}_{n}})]}}^{2}}} } } \right\}} }^{2}}$$

with respect to $\kappa$ and $\Delta _{i}^{'}.$ Here, $\kappa \approx 1$ is the scaling factor and $\Delta _{i}^{'}$ are estimates of constant biases in pseudomeasurements. The first radical in the formula for $\Psi$ represents the corrected magnitude of the measured magnetic field strength on a satellite at moment ${{t}_{n}},$ the second radical represents the calculated EMF strength magnitude at point $O$ at the same moment. Function $\Psi$ characterizes the proximity of magnitudes of measured and calculated magnetic-field strength on the span ${{t}_{0}} \leqslant t \leqslant {{t}_{0}} + T.$ To calculate $\Psi$, it is necessary to know the orbital motion of a satellite only. Minimum value ${{\Psi }_{{\min }}}$ of this function provides a preliminary estimate of the accuracy of magnetic measurements.

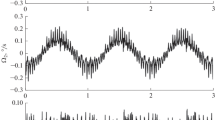
At $T = 210$ min, for the majority of segments of pseudomeasurements, standard deviation ${{\sigma }_{ * }}$ = $\sqrt {{{{{\Psi }_{{\min }}}} \mathord{\left/ {\vphantom {{{{\Psi }_{{\min }}}} {(N - 3)}}} \right. \kern-0em} {(N - 3)}}}$ lies within the limits of 1600–2000γ. In calculating ${{\Psi }_{{\min }}}$ with the use of the actual orbit, ${{\sigma }_{ * }}$ is lower and lies within the limits of 1400–1600γ. Two examples of minimizing function $\Psi$ are presented in Fig. 1. In the upper part of the figure, the EMF strength vector magnitudes calculated from the corrected pseudomeasurements and based on the IGRF model are compared. The calculation from the pseudomeasurements is presented by markers; the calculation based on the IGRF model is presented by solid lines. The plots in the lower part of the figure characterize the deviations of pseudomeasurements from the model. These plots represent the broken lines, the vertices of which correspond to approximation errors. The figure caption indicates the values of ${{\sigma }_{ * }};$ next to them, in parentheses, the values of ${{\sigma }_{ * }},$ obtained using the actual orbital motion are indicated. Pseudomeasurements, the scale of which was corrected by multiplier $\kappa$, were substituted into the functional (3). The values of this multiplier were updated for each processed data segment.

Fig. 1.

Comparison of magnitudes of measured and calculated strength of the EMF. (a) Time moment ${{t}_{0}} = 0{\text{1:39:31}}$ UTC on September 13, 1999, ${{\sigma }_{ * }} = 1561(1374)\gamma ;$ (b) time moment ${{t}_{0}} = {\text{18:50:05}}$ UTC on September 18, 1999, ${{\sigma }_{ * }} = 2059(1649)\gamma .$

Functional (3) was minimized with respect to 11 quantities: the initial conditions for solving system (2) $\psi ({{t}_{0}}),$ $\theta ({{t}_{0}}),$ $\delta ({{t}_{0}}),$ $\Omega ,$ ${{w}_{2}}({{t}_{0}}),$ and ${{w}_{3}}({{t}_{0}})$ and parameters $\lambda ,$ $p,$ $\varepsilon ,$ ${{\alpha }_{c}},$ and ${{\beta }_{c}}.$ The final stage of minimization was performed by the Gauss–Newton method. The accuracy of approximation of pseudomeasurements and the scattering in the estimated quantities were characterized by corresponding standard deviations. Standard deviations were calculated under the assumption that errors in pseudomeasurements $h_{i}^{{(n)}}$ are uncorrelated and have identical variances; the average values of errors in pseudomeasurements with the same lower index i are identical (quantities ${{\Delta }_{i}}$ in (3) represent the estimates of these average values). The standard deviations were calculated as follows. Let ${{\Phi }_{{\min }}}$ be the value of functional (3) at the point of minimum and let $C$ be the matrix of the system of normal equations of the Gauss–Newton method at this point (the matrix $2C$ is approximately equal to the matrix of quadratic form ${{d}^{2}}\Phi$ at the point of minimum of $\Phi$). The variance of errors in pseudomeasurements is then estimated by quantity $\sigma _{H}^{2} = {{{{\Phi }_{{\min }}}} \mathord{\left/ {\vphantom {{{{\Phi }_{{\min }}}} {(3N - 11)}}} \right. \kern-0em} {(3N - 11)}}.$ Standard deviations of estimated quantities are equal to the square roots of corresponding diagonal elements of matrix $\sigma _{H}^{2}{{C}^{{ - 1}}}.$ We denote these standard deviations as ${{\sigma }_{\psi }},$ ${{\sigma }_{\theta }},$ ${{\sigma }_{\delta }},$ ${{\sigma }_{\Omega }},$ ${{\sigma }_{{w2}}},$ ${{\sigma }_{{w3}}},$ ${{\sigma }_{\lambda }},$ ${{\sigma }_{p}},$ ${{\sigma }_{\varepsilon }},$ ${{\sigma }_{{\alpha c}}},$ and ${{\sigma }_{{\beta c}}}.$

The motion of the Photon-12 satellite was reconstructed over 25 time intervals [5]. Some reconstruction results related to intervals 10–25 are given in Table 1; the reconstructions of motion on intervals 14 and 17 are presented in Figs. 2–4. Universal Coordinated Time (UCT) was used in captions to the figures and in the table. Table 1 presents the initial points of intervals ${{t}_{0}}$ and their actual length T. Nominal length $T = 210$ min was chosen in such a way that the obtained values of ${{\sigma }_{H}}$ were no more than double the typical values of ${{\sigma }_{ * }}$ indicated above, or, in other words, in order that the accepted model of motion be sufficiently adequate. Because the accepted model is simplified, it was used to reconstruct the motions of a satellite with a noticeable angular velocity, which arose several (~2) days after the uncontrolled motion beginning. Table 1 contains the data for the intervals, on which the angular velocity was high enough.

Table 1.   Results of processing EMF measurements on the Photon-12 satellite

Fig. 2.

Approximation of magnetic measurements: (a) on interval 14, ${{\sigma }_{H}} = 2043\gamma ;$ (b) on interval 17, ${{\sigma }_{H}} = 1924\gamma .$

Fig. 3.

Angular-velocity components w₂ and w₃ (a) on interval 14, $0.9364 \leqslant {{\omega }_{1}} \leqslant \;0.9395$°/s; (b) on interval 17, $1.0074 \leqslant {{\omega }_{1}} \leqslant \;1.0124$°/s.

Fig. 4.

Angles specifying the direction of the axis $O{{x}_{1}}$ (a) on interval 14; (b) on interval 17.

Figure 2 illustrates the typical quality of the approximation of pseudomeasurements. Here, solid lines depict the plots of functions ${{h}_{i}}(t)$ at ${{t}_{0}} \leqslant t \leqslant {{t}_{0}} + T,$ with markers indicating points $\left( {{{t}_{n}},h_{i}^{{(n)}} - {{\Delta }_{i}}} \right),$ $n = 0,1,2,...,N.$ Quantitatively, the approximation of pseudomeasurements is characterized by standard deviations ${{\sigma }_{H}},$ the values of which are given in Table 1 and in the figure caption. The values of ${{\sigma }_{H}}$ in Table 1 are slightly higher than those in [1]. Nevertheless, the achieved accuracy is sufficient for the purposes of this work.

Figure 3 shows the plots of the angular velocity components ${{w}_{2}}$ and ${{w}_{3}}.$ The component of angular velocity ${{\omega }_{1}}$ in the motion shown in Fig. 3a monotonically decreases, while it grows monotonically in the motion shown in Fig. 3b. The limits of variation of this variable are indicated in the figure caption.

As the component of ${{\omega }_{1}}$ increased, the motion of a satellite became more and more similar to the regular Euler precession of an axisymmetric solid body. The formation of a regular precession with slowly increasing angular velocity ${{\omega }_{1}}$ and slightly changing value of ${{\omega }_{ \bot }} = \sqrt {w_{2}^{2} + w_{3}^{2}}$ was completed after several days of flight.

The accurate regular Euler’s precession can take place only in the case in which a satellite is axisymmetric, and the major torque of external forces, applied to it, is zero. Then, quantities ${{\omega }_{1}}$ and $\omega {}_{ \bot }$ remain unchanged during the motion. For the used model, the first condition was met, while the second one was not. For this reason, we can only say about the motions close to the regular precession. It is convenient to characterize such motions by the following quantities:

$${{{{\bar {\omega }}}}_{ \bot }} = \frac{1}{T}\int\limits_{{{t}_{0}}}^{{{t}_{0}} + T} {{{\omega }_{ \bot }}{\kern 1pt} dt} ,\,\,\,\,{{\delta }}{{{{\omega }}}_{ \bot }} = {{\left[ {\frac{1}{T}\int\limits_{{{t}_{0}}}^{{{t}_{0}} + T} {{{{({{{{\omega }}}_{ \bot }} - {{{{{\bar {\omega }}}}}_{ \bot }})}}^{2}}} dt} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$$

as well as by quantities ${{\bar {\omega }}_{1}}$ and $\delta {{\omega }_{1}}$, determined by similar formulas. For the latter ones, the following formulas apply:

$${{\bar {\omega }}_{1}} = \Omega + \frac{{\varepsilon T}}{2},\,\,\,\,\delta {{\omega }_{1}} = \frac{{\left| \varepsilon \right|T}}{{2\sqrt 3 }}.$$

Standard deviations $\delta {{\omega }_{1}}$ and $\delta {{\omega }_{ \bot }}$ characterize the proximity of the satellite’s motion to a regular precession with parameters ${{\bar {\omega }}_{1}}$ and ${{\bar {\omega }}_{ \bot }}.$ The values of quantities ${{\bar {\omega }}_{1}},$ $\delta {{\omega }_{1}},$ ${{\bar {\omega }}_{ \bot }}$, and $\delta {{\omega }_{ \bot }}$ are indicated in Table 1.

Figure 4 shows the plots of the time dependence of angles $\psi$ and $\theta$ specifying the $O{{x}_{1}}$ axis position with respect to coordinates $O{{X}_{1}}{{X}_{2}}{{X}_{3}}.$ These angles were calculated using the formulas

$$\begin{gathered} \cos \theta = \sqrt {a_{{32}}^{2} + a_{{33}}^{2}} ,\,\,\,\,\sin \theta = - {{a}_{{31}}}, \\ \cos \psi = \frac{{{{a}_{{11}}}}}{{\sqrt {a_{{11}}^{2} + a_{{21}}^{2}} }},\,\,\,\,\sin \psi = \frac{{{{a}_{{21}}}}}{{\sqrt {a_{{11}}^{2} + a_{{21}}^{2}} }}. \\ \end{gathered} $$

The satellite motion over the angles became stable by interval 7 only, with the $O{{x}_{1}}$ axis ceasing to intersect the orbital plane and remaining located in the half-space Z₂ > 0 during the entire subsequent flight. The motion in Figs. 3 and 4 is already clearly similar to the regular Euler precession.

Additional information about the satellite motion is provided in Fig. 5. Here, for the two reconstructions discussed above, the plots are presented for angle $\alpha$ between the $O{{x}_{1}}$ axis and the vector of the angular momentum of a satellite in its motion relative to the center of masses, as well as for angle $\rho$ between this vector and the axis $O{{X}_{2}}.$ In the regular Euler precession, $\alpha = {\text{const}}{\text{.}}$ In the examples in Fig. 5, this angle varies within fairly narrow limits, near the values ${{\alpha }_{ * }} = {\text{arctan(}}{{{{{\bar {\omega }}}_{ \bot }}} \mathord{\left/ {\vphantom {{{{{\bar {\omega }}}_{ \bot }}} {\lambda {{{\bar {\omega }}}_{1}}}}} \right. \kern-0em} {\lambda {{{\bar {\omega }}}_{1}}}}{\text{)}}{\text{,}}$ which are indicated in the figure caption. The angular momentum vector oscillates near the $O{{X}_{2}}$ axis (see the plots of angle $\rho$), the angular velocity of which is less than 5°/day. Motions of such a type took place on September 15–19—on intervals 10 and 14–18, in particular. The estimates of parameters $p,$ $\lambda ,$ $\varepsilon ,$ ${{\alpha }_{c}},$ and ${{\beta }_{c}}$ and their standard deviations for these intervals are presented in Table 2. Here, the angles are expressed in radians, while quantities $p$ and $\varepsilon$ are presented in units of 10^–6 s^–2. The data in this table are typical for all intervals 1–25 [5]. The standard deviations of initial conditions of reconstructions on intervals 1–25, expressed in radians and 0.001 s^–1, lie in the ranges [5] ${{\sigma }_{\delta }} = 0.01{\kern 1pt} - {\kern 1pt} 0.025,$ ${{\sigma }_{{\theta ,\psi }}} = 0.01{\kern 1pt} - {\kern 1pt} 0.02,$ ${{\sigma }_{\Omega }} = 0.01{\kern 1pt} - {\kern 1pt} 0.025,$ and ${{\sigma }_{{w2,w3}}} = 0.02{\kern 1pt} - {\kern 1pt} 0.08.$ These examples shows an approximation of pseudomeasurements that is less accurate than in [1, 3]. The values of ${{\sigma }_{H}}$ in Table 1 are slightly higher than in [1, 3]. Nevertheless, the reconstructions of this work reproduce all features of a satellite’s rotational motion.

Fig. 5.

Satellite angle of nutation $\alpha$and angle $\rho$ between the vector of satellite’s angular momentum relative to the center of masses and the axis $O{{X}_{2}}$ (a) on interval 14, ${{\alpha }_{ * }} = 35.4^\circ ;$ (b) on interval 17, ${{\alpha }_{ * }} = 24.3^\circ .$

Table 2.   Estimates and standard deviations of parameters of equations of motion

Intervals 10 and 14–18 are of particular interest for the further analysis, because the motions on them allow an acceptable approximation of a generalized-conservative mechanical system by periodic motions.

GENERALIZED-CONSERVATIVE MODEL OF A SATELLITE ROTATIONAL MOTION

As can be seen from Table 1, the values of ${{\bar {\omega }}_{1}}$ have stabilized over time. Apparently, the moment of resistance proportional to ${{\omega }_{1}}$ [1], which was disregarded in Eqs. (2), has grown. On intervals from that part of Table 1 in which the values of $\varepsilon$ are low, the solutions of Eqs. (2) can be used to reconstruct the satellite motion for $\varepsilon = 0.$ The plots illustrating such reconstruction on intervals 10 and 14–18 are given in [5]. They are very similar to the plots obtained with using the original system (2), but have the increased values of ${{\sigma }_{H}}.$ These values, on indicated intervals, are presented in Table 3 together with the estimates of quantities $\Omega ,$ $p,$ $\lambda ,$ ${{\alpha }_{c}},$ ${{\beta }_{c}}$ and their standard deviations. In this table, $[\Omega ] = 0.001\,\,{{{\text{s}}}^{{ - 1}}}$ and $[p] = {{10}^{{ - 6}}}\,\,{{{\text{s}}}^{{ - 2}}}.$ The comparison of the data in Tables 2 and 3 allows one to understand what benefit was provided by coarsening the model. The values of $\Omega$ found during the new processing are very close to corresponding values of ${{\bar {\omega }}_{1}}$ from Table 1.

Table 3.   Estimates and standard deviations of parameters of equations of motion for $\varepsilon = 0$

Below, in this Section, we let, in (2), $\varepsilon = 0$ and ${{\omega }_{1}} = \Omega$ and assume $\Omega$ to be a parameter. We supplement Eqs. (2) with the Poisson equations for the components of the unit vector (ort) of the $O{{X}_{2}}$ axis in the system $O{{x}_{1}}{{x}_{2}}{{x}_{3}}{\text{,}}$

$$\begin{gathered} {{{\dot {a}}}_{{21}}} + {{w}_{2}}{{a}_{{23}}} - {{w}_{3}}{{a}_{{22}}} = 0,\,\,\,\,{{{\dot {a}}}_{{22}}} + {{w}_{3}}{{a}_{{21}}} = 0, \\ {{{\dot {a}}}_{{23}}} - {{w}_{2}}{{a}_{{21}}} = 0, \\ \end{gathered} $$

and denote the resulting system by (2a). Equations (2a) allow for the generalized integral of energy

$$\begin{gathered} \frac{1}{2}\left( {w_{2}^{2} + w_{3}^{2}} \right) - {{\omega }_{0}}(\lambda \Omega {{a}_{{21}}} + {{w}_{2}}{{a}_{{22}}} + {{w}_{3}}{{a}_{{23}}}) \\ - \,\,\frac{3}{2}\omega _{0}^{2}(1 - \lambda )a_{{31}}^{2} - p{{a}_{{11}}}; \\ \end{gathered} $$

that is, the satellite represents a generalized-conservative mechanical system. Equations (2a) also have the families of partial solutions, in which ${{a}_{{i1}}}$ are constant quantities bound by the relations

$$\begin{gathered} a_{{11}}^{2} + a_{{21}}^{2} + a_{{31}}^{2} = 1,\,\,\,\,{{a}_{{31}}}\left[ {3\omega _{0}^{2}(1 - \lambda ){{a}_{{11}}} + p} \right] = 0, \\ {{\omega }_{0}}({{\omega }_{0}}{{a}_{{21}}} - \lambda \Omega )\left( {1 - a_{{21}}^{2}} \right) \\ + \,\,{{a}_{{21}}}\left[ {3\omega _{0}^{2}(1 - \lambda )a_{{31}}^{2} - p{{a}_{{11}}}} \right] = 0, \\ \end{gathered} $$

(4)

while the remaining elements of matrix $\left\| {{{a}_{{ij}}}} \right\|$ are determined by the relations

$$\begin{gathered} {{{\dot {a}}}_{{22}}} + {{\omega }_{0}}{{a}_{{21}}}{{a}_{{23}}} = 0,\,\,\,\,{{{\dot {a}}}_{{23}}} - {{\omega }_{0}}{{a}_{{21}}}{{a}_{{22}}} = 0, \\ {{a}_{{12}}} = \frac{{{{a}_{{31}}}{{a}_{{23}}} - {{a}_{{11}}}{{a}_{{21}}}{{a}_{{22}}}}}{{1 - a_{{21}}^{2}}},\,\,\,\,{{a}_{{13}}} = - \frac{{{{a}_{{31}}}{{a}_{{22}}} + {{a}_{{11}}}{{a}_{{21}}}{{a}_{{23}}}}}{{1 - a_{{21}}^{2}}}, \\ {{a}_{{32}}} = - \frac{{{{a}_{{11}}}{{a}_{{23}}} + {{a}_{{31}}}{{a}_{{21}}}{{a}_{{22}}}}}{{1 - a_{{21}}^{2}}},\,\,\,\,{{a}_{{33}}} = \frac{{{{a}_{{11}}}{{a}_{{22}}} - {{a}_{{31}}}{{a}_{{21}}}{{a}_{{23}}}}}{{1 - a_{{21}}^{2}}}. \\ \end{gathered} $$

(5)

Let the relations (4) be fulfilled. Equations (5) for variables ${{a}_{{22}}}$ and ${{a}_{{23}}}$ have the solution ${{a}_{{22}}}$   =  $\sqrt {1 - a_{{21}}^{2}} \cos [{{a}_{{21}}}{{\omega }_{0}}(t - {{t}_{0}})]$ and ${{a}_{{23}}}$ = $\sqrt {1 - a_{{21}}^{2}} \sin [{{a}_{{21}}}{{\omega }_{0}}(t - {{t}_{0}})],$ where ${{t}_{0}}$ is an arbitrary constant; variables ${{a}_{{12}}},$ ${{a}_{{13}}},$ ${{a}_{{32}}},$ and ${{a}_{{33}}}$ are found by formulas (5). The ort of the Ox₁ axis in the OX₁X₂X₃ system has components ${{a}_{{i1}}},$ and, as a result, solutions (4), (5) describe the state of rest of the Ox₁ axis in this system. For $p = 0$, these solutions coincide with known solutions, called conical, cylindrical and hyperboloidal precessions [6]. Their complicated shape and the unexpected period are associated with the method of introducing the coordinate system Oy₁y₂y₃. This system, which is suitable in the task of processing magnetic measurements, is poorly suited for describing the satellite motion relative to the orbital coordinate system. It turned out that, in intervals 10 and 14–18, the periodic motions of specific form could be used for reconstruction. However, to obtain them, Eqs. (2a) must be replaced by equivalent equations in other variables.

To describe the satellite motions in which the Ox₁ axis declines from the $O{{X}_{2}}$ axis by less than 90°, the position of the Ox₁x₂x₃ system with respect to the OX₁X₂X₃ system can be conveniently specified by angles $\psi$ and $\theta$ introduced above, as well as by the third angle $\varphi ,$ the turn at which around the $O{{x}_{1}}$ axis completes the transformation of the OX₁X₂X₃ system into the Ox₁x₂x₃ system. The transformation OX₁X₂X₃ → Ox₁x₂x₃ can be presented as a superposition of transformations OX₁X₂X₃ → Oy₁y₂y₃ and Oy₁y₂y₃ → Ox₁x₂x₃. The first transformation is specified by angles $\psi ,$ $\theta$, and $\delta ,$ and the second transformation is specified by angle $\chi .$ The turns at angles $\delta$ and $\chi$ are performed around the $O{{x}_{1}} = O{{y}_{1}}$ axis in the same direction; as a result, $\varphi = \delta + \chi .$

If we are interested only in the motion of satellite’s axis of symmetry $O{{x}_{1}},$ it is convenient to use angles $\psi$ and $\theta$, as well as combinations of angular velocities

$$\begin{gathered} {{\Omega }_{2}} = {{\omega }_{2}}\cos \varphi - {{\omega }_{3}}\sin \varphi = {{w}_{2}}\cos \delta - {{w}_{3}}\sin \delta , \\ {{\Omega }_{3}} = {{\omega }_{2}}\sin \varphi + {{\omega }_{3}}\cos \varphi = {{w}_{2}}\sin \delta + {{w}_{3}}\cos \delta , \\ \end{gathered} $$

where

$$\cos \delta = \frac{{{{a}_{{33}}}}}{{\sqrt {a_{{32}}^{2} + a_{{33}}^{2}} }},\,\,\,\,\sin \delta = \frac{{{{a}_{{32}}}}}{{\sqrt {a_{{32}}^{2} + a_{{33}}^{2}} }}.$$

Such variables were used in [2]. Examples of plots of angular velocities $\dot {\delta },$ ${{\Omega }_{2}},$ and ${{\Omega }_{3}}$ in reconstructions on intervals 14 and 17 are presented in Fig. 6. Quantities ${{\Omega }_{2}}$ and ${{\Omega }_{3}}$ are the projections of satellite’s angular velocity on the Resale axes, corresponding to angles $\psi$ and $\theta .$

Fig. 6.

Angular velocities $\dot {\delta },{{\Omega }_{2}},{{\Omega }_{3}}$ (a) on interval 14; (b) on interval 17.

PERIODIC MOTIONS OF THE AXIS OF SYMMETRY OF A SATELLITE

The following equations are valid for variables $\psi ,$ $\theta ,$ ${{\Omega }_{2}},$ and ${{\Omega }_{3}}$ [2]:

$$\begin{gathered} \dot {\theta } = {{\Omega }_{2}} - {{\omega }_{0}}\cos \psi ,\,\,\,\,\dot {\psi } = \frac{{{{\Omega }_{3}}}}{{\cos \theta }} - {{\omega }_{0}}{\text{tan}}\theta \sin \psi , \\ {{{\dot {\Omega }}}_{2}} = - \left( {\lambda \Omega + {{\Omega }_{3}}{\text{tan}}\theta - {{\omega }_{0}}\frac{{\sin \psi }}{{\cos \theta }}} \right){{\Omega }_{3}} + 3\omega _{0}^{2}(1 - \lambda ) \\ \times \,\,\sin \theta \cos \theta + p\cos \psi \sin \theta , \\ {{{\dot {\Omega }}}_{3}} = \left( {\lambda \Omega + {{\Omega }_{3}}{\text{tan}}\theta - {{\omega }_{0}}\frac{{\sin \psi }}{{\cos \theta }}} \right){{\Omega }_{2}} + p\sin \psi . \\ \end{gathered} $$

(6)

The solutions of system (2a), expressed in terms of $\psi ,$ $\theta ,$ ${{\Omega }_{2}}$ and ${{\Omega }_{3}}$ on intervals 10 and 14–18, are similar to periodic solutions of system (6), studied in [2]. Solutions on these intervals differ from solutions on the other intervals in the fact, that the angular momentum of satellite’s motion relative to the center of masses only slightly deviates from the normal to the orbital plane.

System (6) is invariant with respect to the transformation of variables $t \to - t,$ $\theta \to - \theta ,$ ${{\Omega }_{3}} \to - {{\Omega }_{3}};$ so, we can search for solutions of it in which variables $\theta$ and ${{\Omega }_{3}}$ are odd, and variables $\psi$ and ${{\Omega }_{2}}$ are even, functions of time. Periodic solutions with such properties are called “symmetric.” Symmetric periodic solutions with period $T$ are defined by the boundary conditions

$$\theta (0) = {{\Omega }_{3}}(0) = \theta \left( {\frac{T}{2}} \right) = {{\Omega }_{3}}\left( {\frac{T}{2}} \right) = 0.$$

(7)

In [2], the symmetric periodic solutions of system (6) are constructed, which are continued from the Lyapunov solutions existing in the vicinity of its stationary solution $\theta = 0,$ $\psi = \psi (p),$ $\left| p \right| \leqslant 0.5,$ $\psi (0) = \pi {\text{/}}2.$ For $p = 0$, this stationary solution transfers into the cylindrical precession. There exist two families of such periodic solutions, called “short-periodic” and “long-periodic.”

Short-periodic solutions were used for approximation. Parameters $p,$ $\lambda ,$ and $\Omega$ of system (6) for each approximated interval were determined as a result of processing magnetic measurements (Table 3). The value of period $T$was found as a result of spectral analysis of the solutions of system (2a), which approximate magnetic measurements on interval under study. The variables of system (2a) in this solution were recalculated by the method described above into functions θ(t), $\psi (t),$ ${{\Omega }_{2}}(t),$ and ${{\Omega }_{3}}(t),$ and the trial period was determined for each of these functions. Now, we describe the determination of a trial period for the example of function θ(t). This function (as well as the rest of the ones from the given set) was calculated on the uniform time grid $\left\{ {t_{m}^{'}} \right\}_{{m = 0}}^{M},$ $t_{m}^{'} = {{t}_{0}} + mh,$ $h = 20$ s, $(M - 1)h < T \leqslant Mh.$ Then, the approximation of this function was constructed by the expression

$${{\theta }_{{{\text{ap}}}}}(t) = {{a}_{0}} + a\cos 2\pi ft + b\sin 2\pi ft,$$

(8)

where ${{a}_{0}},$ $a,$ $b$, and $f$ are parameters. The values of parameters were sought by the least-squares method by minimizing the expression

$$\Psi ({{a}_{0}},a,b,f) = {{\sum\limits_{m = 0}^M {\left[ {\theta \left( {t_{m}^{'}} \right) - {{\theta }_{{{\text{ap}}}}}\left( {t_{m}^{'}} \right)} \right]} }^{2}}.$$

Minimization was carried out in two stages. First, as a result of solving a number of identical linear least-squares problems, we calculated the values of the function

$$\begin{gathered} {{\Psi }_{1}}(f) = \min \Psi ({{a}_{0}},a,b,f) \\ {{a}_{0}},a,b \\ \end{gathered} $$

at the nodes of a sufficiently fine uniform grid on the segment $0 \leqslant f \leqslant {{10}^{{ - 3}}}$ Hz. We then found, on this grid, point ${{f}_{{\min }}} = \arg \min {{\Psi }_{1}}(f).$ The trial period was determined by formula $T = {1 \mathord{\left/ {\vphantom {1 {{{f}_{{\min }}}}}} \right. \kern-0em} {{{f}_{{\min }}}}}{\kern 1pt} .$ If function ${{\Psi }_{1}}(f)\,$ has several significant minima, then the variable under study θ(t) contains several components of form (8). In this case, the periodic approximation may occur to be impossible.

On intervals 10 and 14–18, functions ${{\Psi }_{1}}(f)$ for variables θ(t), $\psi (t),$ ${{\Omega }_{2}}(t),$ and ${{\Omega }_{3}}(t)$ had only one significant minimum, with the values of $\min {{\Psi }_{1}}$ differing from the values of these functions outside the small neighborhood of point ${{f}_{{\min }}}$ (they are close to $\max {{\Psi }_{1}}$) by ten times or more [5].

The trial periods found by functions θ(t), $\psi (t),$ ${{\Omega }_{2}}(t)$, and ${{\Omega }_{3}}(t)$ coincide quite precisely. Since variables ${{\Omega }_{2}}$ and $\Omega$₃ have changed most intensively in the motions on intervals 10 and 14–18, the trial period was determined from the periodograms of functions ${{\Omega }_{2}}(t)$ and ${{\Omega }_{3}}(t).$ For them, the values of ${{f}_{{\min }}}$ fell into the same nodes of a grid with a step of 2 × 10^–7 Hz. The found value of the trial period was used to construct an approximating solution of boundary-value problem (6), (7). This problem was solved by the targeting method (see [2]). The amplitudes of corresponding expressions (8) served as an initial approximation of unknown initial conditions $\psi (0)$ and ${{\Omega }_{2}}(0)$ for $f = {{f}_{{\min }}}.$ One can also use the values of variables $\psi$ and ${{\Omega }_{2}}$ in the approximate solution at point ${{t}_{ * }},$ determined by the relation $\theta ({{t}_{ * }}) \approx 0.$

Examples of constructed periodic solutions are given in Figs. 7 and 8 and in Table 4. The table indicates the parameters of solutions of problem (6) and (7) $T{\text{/}}2,$ $\psi (0)$, and ${{\Omega }_{2}}(0)$, as well as orbital frequency ${{\omega }_{0}}$ on the given interval and coefficient $a$ in the characteristic equation ${{(\rho - 1)}^{2}}({{\rho }^{2}} - 2a\rho + 1) = 0,$ which determines the multipliers of a periodic solution. Here, the unit of measurement of time is 1000 s, the unit of measurement of the angular velocity is 0.001 s^–1. As we can see, all found periodic solutions are orbitally stable in the first approximation. The figures present the plots of variables θ(t), $\psi (t),$ ${{\Omega }_{2}}(t)$, and ${{\Omega }_{3}}(t)$ in the periodic solutions on the span $0 \leqslant t \leqslant 2T$and the projections of the ort of the axis $O{{x}_{1}}$ and of the ort of the satellite’s angular momentum on the plane $O{{X}_{1}}{{X}_{3}}.$ The projection of the ort of the angular momentum lies inside the projection of the ort of the axis $O{{x}_{1}}.$

Fig. 7.

Periodic solutions used to approximate the motion of a satellite (a) on interval 14, (b) on interval 17.

Fig. 8.

Projections of hodographs of orts of the axis $O{{x}_{1}}$ (outer curves) and of the angular momentum of rotational motion (inner curves) on the plane $O{{X}_{1}}{{X}_{3}}$ (a) on interval 14, (b) on interval 17.

The comparison of the motions, found by processing magnetic measurements, and the periodic solutions was carried out according to the following scheme. Variables θ(t), $\psi (t),$ ${{\Omega }_{2}}(t)$, and ${{\Omega }_{3}}(t)$ in the periodic solution were approximated by the discrete Fourier series [7]. The even functions were expanded in a series in cosines, while the odd functions were expanded in a series in sines. Two hundred harmonics were used in each approximating expression. We denote the constructed series as $\tilde {\theta }(t),$ $\tilde {\psi }(t),$ ${{\tilde {\Omega }}_{2}}(t)$, and ${{\tilde {\Omega }}_{3}}(t).$ We then composed the expression

$$\begin{gathered} F(\tau ) = \sum\limits_{m = 0}^M {\left\{ {{{{\left[ {\theta \left( {t_{m}^{'}} \right) - \tilde {\theta }(t_{m}^{'} - {{t}_{0}} - \tau )} \right]}}^{2}}} \right.} \\ + \,\,{{\left[ {\psi \left( {t_{m}^{'}} \right) - \tilde {\psi }\left( {t_{m}^{'} - {{t}_{0}} - \tau } \right)} \right]}^{2}} \\ + \,\,{{\left[ {{{\Omega }_{2}}\left( {t_{m}^{'}} \right) - {{{\tilde {\Omega }}}_{2}}\left( {t_{m}^{'} - {{t}_{0}} - \tau } \right)} \right]}^{2}} \\ \left. { + \,\,{{{\left[ {{{\Omega }_{3}}\left( {t_{m}^{'}} \right) - {{{\tilde {\Omega }}}_{3}}\left( {t_{m}^{'} - {{t}_{0}} - \tau } \right)} \right]}}^{2}}} \right\}, \\ \end{gathered} $$

which was minimized in $\tau$ on a fairly fine grid. The values of $\tau$ found in this way are presented in Table 4. The left part of Figs. 9–14 presents the plots of functions θ(t), $\psi (t),$ ${{\Omega }_{2}}(t)$, and ${{\Omega }_{3}}(t)$ in unified coordinate systems, as well as the corresponding approximating expressions $\tilde {\theta }(t - {{t}_{0}} - \tau ),$ $\tilde {\psi }(t - {{t}_{0}} - \tau ),$ ${{\tilde {\Omega }}_{2}}(t - {{t}_{0}} - \tau ),$ and ${{\tilde {\Omega }}_{3}}(t - {{t}_{0}} - \tau ).$ The right part of these figures presents the plots of differences $\Delta \theta = \theta (t) - \tilde {\theta }(t - {{t}_{0}} - \tau ),$ etc. All plots are constructed from the values on the grid $\left\{ {t_{m}^{'}} \right\}_{{m = 0}}^{M}.$ As one can see, the periodic approximation turned out to be quite accurate. Judging by the plots, functions $\Delta \theta (t)$ and $\Delta \psi (t)$ contain a low-frequency component, which, apparently, is somehow associated with long-period Lyapunov solutions [2].

Table 4.   Parameters of periodic solutions

Fig. 9.

Approximation of satellite motion on interval 10 by a periodic solution.

Fig. 10.

Approximation of satellite motion on interval 14 by a periodic solution.

Fig. 11.

Approximation of satellite motion on interval 15 by a periodic solution.

Fig. 12.

Approximation of satellite motion on interval 16 by a periodic solution.

Fig. 13.

Approximation of satellite motion on interval 17 by a periodic solution.

Fig. 14.

Approximation of a satellite motion on interval 18 by a periodic solution.

During the flight of Photon-12, a rare situation occurred in which the actual, rather complicated rotational motions of a satellite could be approximated by periodic solutions of the equations of motion of a generalized-conservative mechanical system. This fact serves as another justification to the use of simplified mathematical models in the problems of space-flight mechanics.