Abstract
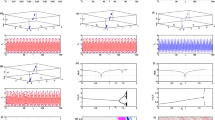
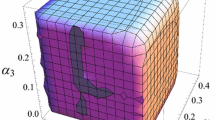
The dynamic model of price competition in which processes of strategic interaction between companies on an imperfect competition market are described with the game-theoretic approach and methods of nonlinear dynamics. The pricing dynamics for the companies is modeled with difference equations (mappings). We study the stability of the fixed point of the price mapping. Results of our numerical modeling have shown the existence of periodic and chaotic solutions in the price competition model. We present intra-company adaptation mechanisms based on changing the prices in a way proportional to the rate of change in the companies’ profits; this lets us reduce the prices to a local Nash equilibrium and stabilize the chaotic dynamics of the market.
Similar content being viewed by others
References
Orlova, E.V., Efficient Pricing Mechanism for the Product of Industrial Companies, Ekonom. Predprinimatel’stvo, 2013, no. 12–1, pp. 622–626.
Kaneman, D., Rational Choice, Values, and Frames, Psikhologich. Zh., 2003, vol. 24, no. 4, pp. 31–42.
Orlova, E.V., Modeling the Utility Function with Irrational Factors, Nauch.-Tekhn. Vedomosti S.-Peterburg. Gos. Politekhn. Univ., Ekonom. Nauki, 2012, no. 3, pp. 24–30.
Orlova, E., Economical Behavior: A Synthesis of Rational and Irrational, Probl. Teorii Praktiki Upravlen., 2014, no. 3, pp. 127–136.
Petrosyan, L.A., Zenkevich, N.A., and Shevkoplyas, E.V., Teoriya igr (Game Theory), St. Petersburg: BKhV-Peterburg, 2012.
Zenkevich, N.A., Petrosyan, L.A., and Yang, D.V.K., Dinamicheskie igry i ikh prilozheniya v menedzhmente (Dynamical Games and Their Applications in Management), St. Petersburg: Vysshaya Shkola Menedzhmenta, 2009.
Filatov, A.Yu. and Aizenberg, N.I., Matematicheskie modeli nesovershennoi konkurentsii (Mathematical Models of Imperfect Competition), Irkutsk: IGU, 2012.
Axelrod, R., The Evolution of Cooperation, New York: Basic Book, 1984.
Vuros, A. and Rozanova, N., Ekonomika otraslevykh rynkov (Economics of Industrial Markets), Moscow: TEIS, 2002.
Vasin, A.A. and Morozov, V.V., Teoriya igr i modeli matematicheskoi ekonomiki (Game Theory and Models of Mathematical Economics), Moscow: MAKS Press, 2005.
Puu, T., Nonlinear Economic Dynamics, New York: Springer, 1997.
Lorenz, H.-W., Nonlinear Dynamical Economics and Chaotic Motion, Berlin: Springer-Verlag, 1989.
Kuznetsov, S.P., Dinamicheskii khaos (Dynamical Chaos), Moscow: Fizmatlit, 2006.
Loskutov, A.Yu. and Mikhailov, A.S., Osnovy teorii slozhnykh sistem (Fundamentals of the Theory of Complex Systems), Moscow–Izhevsk: Inst. Komp’yut. Issled., 2007.
Neimark, Yu.I., Dinamicheskie sistemy i upravlyaemye protsessy (Dynamical Systems and Controllable Processes), Moscow: Librokom, 2010.
Kuznetsov, A.P., Savin, A.V., Sedova, Yu.V., et al., Bifurkatsii otobrazhenii (Bifurcations of Mappings), Saratov: Izd. Tsentr “Nauka,” 2012.
Ostrovskii, A.V., On One Class of Competitive Pricing Models in a Market Economy, Differ. Uravn. Prots. Upravlen., 2000, no. 2, pp. 58–77, URL: http://www.math.spbu.ru/diffjournal/pdf/j058.pdf (accessed at 06.03.2015).
Loskutov, A.Yu., Nonlinear Optimization of the Market’s Chaotic Dynamics, Ekonom. Mat. Metod., 2010, vol. 46, no. 3, pp. 58–70.
Holyst, J.A. and Urbanowicz, K., Chaos Control in Economical Model by Time-Delayed Feedback Method, Physica A, 2000, vol. 287, pp. 587–598.
Kopel, M., Improving the Performance of an Economic System: Controlling Chaos, J. Evolutionary Econ., 1997, vol. 7, pp. 269–289.
Ahmed, E. and Hassan, S.Z., On Controlling Chaos in Sournot-Games with Two and Three Competitors, Nonlin. Dynamics, Psychology, Life Sci., 2000, vol. 4, no. 2, pp. 189–194.
Ahmed, E., Elsadany, A.A., and Puu, T. On Bertrand Duopoly Game with Differentiated Goods, Appl. Math. Comput., 2015, vol. 251, pp. 169–179.
Feichtinger, G., Economic Evolution and Demographic Change, Berlin: Springer, 1992.
Agliari, A., Gardini, L., and Puu, T., Global Bifurcations in Duopoly when the Cournot Point is Destabilized through a Subcritical Neimark Bifurcation, Working paper, 2003, URL: http://www.cerum.umu.se/ digitalAssets/18/18883 cwp 66 03.pdf (accessed at 04.03.2015).
Stachurski, D., Economic Dynamics: Theory and Computation, Cambridge: MIT Press, 2009.
Puu, T., Attractors, Bifurcations, and Chaos: Nonlinear Phenomena in Economics, New York: Springer, 2003, 2nd ed.
Neimark, Yu.I. and Ostrovskii, A.V., On Certain Pricing Models in a Market Economy, Izv. Yyssh. Uchebn. Zaved., Prikl. Nelin. Dinam., 1999, no. 6, pp. 35–41.
Ferguson, B.S. and Lim, G.C., Dynamic Economic Models in Discrete Time: Theory and Empirical Applications, New York: Taylor & Francis e-Library, 2005.
Schuster, G., Deterministic Chaos: An Introduction, Weinheim: Physik-Verlag, 1984. Translated under the title Determinirovannyi khaos. Vvedenie, Moscow: Mir, 1988.
Farmer, J.D., Ott, E., and Yorke, J.A., The Dimension of Chaotic Attractors, Physica 7D, 1983, pp. 153–180.
Moon, F., Chaotic Vibrations: An Introduction for Applied Scientists and Engineers, New York: Wiley, 1987. Translated under the title Khaoticheskie kolebaniya. Vvodnyi kurs dlya nauchnykh rabotnikov i inzhenerov, Moscow: Mir, 1990.
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © E.V. Orlova, 2017, published in Avtomatika i Telemekhanika, 2017, No. 1, pp. 19–34.
This paper was recommended for publication by A.L. Fradkov, a member of the Editorial Board
Rights and permissions
About this article
Cite this article
Orlova, E.V. Control over chaotic price dynamics in a price competition model. Autom Remote Control 78, 16–28 (2017). https://doi.org/10.1134/S0005117917010027
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0005117917010027