Introduction

Throughout the history of music, compositional practices and styles have changed. This simple fact involves the more complex question of what it is that changes. Addressing this question, music theorists and historians have since long provided detailed accounts of characteristics common to different pieces from the same composer or era and have used these features as the basis for distinguishing between different styles (Meyer, 1989; Nattiez, 1990), e.g., the style of the Baroque or the Romantic eras. Historical changes of style lie, in fact, at the heart of the historiography of Western art music (Burkholder et al., 2014; Dannenberg, 2010; Meyer, 1994). These accounts are usually based on selected, prototypical examples that manifest stylistic traits particularly strongly.

In an effort to put these assertions on a more robust empirical foundation, recent years have seen a rise in the development of specific analytical methods and tools for computational analysis and their application to bigger corpora of music with a focus on large-scale diachronic developments. For instance, Weiß et al. (2019) study the concept of musical periods based on a large sample of audio recordings. Extracting a variety of musical features, they investigate chord transitions, intervals, and tonal complexity, and visualize them on so-called evolution curves in order to show diachronical developments. Their findings include that traditional musicological boundaries of historical eras by and large represent differences in musical content well. In agreement with these findings, Nakamura and Kaneko (2019) employ a statistical evolutionary model to discover a steadily increasing trend for dissonant intervals. Moss and Rohrmeier (2021) use the popular computational model Latent Dirichlet Allocation (LDA; Blei et al., 2003) in order to discover topics, operationalized as recurring distributions of pitch classes, in a large historical corpus and trace their prevalence over time, showing that topics resembling diatonic keys are most stable. Harasim et al. (2021) develop a model of musical mode and use Bayesian inference to demonstrate that the number and shape of modes, conceived as transpositional equivalence classes of keys, substantially changes between different periods of music history. Moss et al. (2023) show that the tonal material used in Western classical compositions gradually expands over time on the line-of-fifths (Temperley, 2000), thus allowing for an extended use of more chromatic sonorities.

From a different methodological perspective, Yust (2019) uses the formalism of the discrete Fourier transform (DFT) applied to pitch-class distributions and finds amongst other things that diatonicity decreases significantly in the eighteenth and nineteenth centuries. Viaccoz et al. (2022) use a similar methodology to show that tonal characteristics of different pieces from different composers and time periods are reflected in different coefficients of the DFT. Building on their concept of dynamical score networks, Nardelli et al. (2022) devise an entropy-based measure for harmonic complexity based on information theory. They trace changes in complexity in a large corpus of more than 2000 musical pieces covering more than 500 years and report increasing harmonic complexity.

González-Espinoza et al. (2020) recognize that music can be considered as a time series. Analyzing more than 8000 pieces from different historical periods, they find that musical time series are clearly irreversible because they do not possess simple linear correlation structures (see Moss et al., 2019, for similar findings). The authors interpret this as pointing towards music having a much richer deep structure. Most recently, González-Espinoza and Plotkin (2023) use harmonic complexity measures as well as a novel measure of innovativeness which provides a more detailed account for the Classical era, for which the authors report an initial decrease in harmonic complexity in its early decades, corresponding to the known fact that Classical composers tended to use simpler (i.e., less chromatic) harmonies than Baroque composers. They also report that novelty increases towards the end of the Classical period, in line with music theorists’ understanding of the transition between Classical and Romantic harmony.

On a smaller scale, researchers have also investigated stylistic changes within the lifetime of single composers or genres. For instance, Laneve et al. (2023) recently studied Debussy’s piano works using the DFT and confirmed that the composer gradually changed his style from using more diatonic or pentatonic tonalities towards an increased employment of symmetrical scales, such as the whole-tone or octatonic scales. In Moss et al. (2020b), the authors find an increasing chromaticization of harmonies in Brazilian Choro, most likely due to influences from other genres such as Bossa Nova and Jazz.

In short, a range of approaches have addressed the question of style and stylistic changes in music from a computational perspective using a variety of methodologies. Here, we contribute to this growing line of research by specifically focusing on tonal interval distributions and by posing questions regarding the changing usage of intervals throughout the history of Western music. To that end, we employ the Tonal Diffusion Model (TDM), a recently developed computational model for interval relations in pieces of tonal music (Lieck et al., 2020) that builds on music-theoretical conceptions of tonal space, such as the Tonnetz (see below). Applying this model to a large diachronical corpus, the Tonal Pitch-Class Counts Corpus (TP3C; Moss et al., 2020a), enables us to trace the dynamics of changes in interval distributions that we can then interpret as reflecting underlying stylistic dynamics. One of the main strengths of the model is its conformity to historical music-theoretical conceptualizations of relations between tones, which we briefly review now before specifying the model in more detail.

Tonal spaces

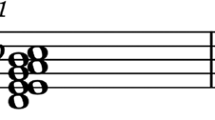
Investigations into the formal or mathematical structure of tonal space have a long history.Footnote 1 The earliest known depiction of a formalization of tone relations dates back to Euler (1739) who devised a spatial diagram of musical intervals (see Fig. 1; a later version was published in Euler, 1774). Euler distinguishes two types of intervals, namely perfect fifths (‘V’) and major thirds (‘III’). He clearly assumes enharmonic equivalence because only twelve octave-equivalent tones are displayed and the note at the very bottom is labeled ‘B’ and not ‘As’, which would have been the enharmonically correct fifth above ‘Ds’ and major third above ‘Fs’ (he notates sharp signs with ‘s’).

Fig. 1: Graphical depiction of tonal relations according to Euler (1839, 147).
figure 1

Sharp accidentals are abbreviated with an ‘s’ instead of ‘♯’, H corresponds to B natural and B corresponds to B♭.

Full size image

Later, several 19th-century music theorists have proposed similar spatial representations for intervallic relations between tones but without assuming enharmonic equivalence (e.g., Hauptmann, 1853; Hostinský, 1879; Riemann, 1896; von Oettingen, 1866; Weitzmann, 1860). These are usually referred to as the Tonnetz (Cohn, 1997; Gollin, 2006; Meeùs, 2020). Most commonly, the nodes of the Tonnetz represent tones, and the edges represent intervals between them.Footnote 2 Between all possibilities, the choice falls most often on the perfect fifth and the major third as intervals spanning the Tonnetz (as in Euler’s diagram), but sometimes also the minor third. Authors usually justify this choice with reference to the harmonic series in which these intervals occur relatively early (Sethares, 2005). Due to their importance, we will call these the primary intervals. This can be traced back to several historical precursors. German music theorist Moritz Hauptmann, for example, understands the intervals of the octave, the perfect fifth, and the major third as being “directly intelligible” and “unchangeable” (Hauptmann, 1853, 5) and takes them as axiomatic for his music-theoretical system of harmony.

Almost a generation later, Czech music theorist Otakar Hostinský postulates that the octave has merely a status as an “Alterego” (Hostinský, 1879, 67), thus rendering octave-related tones as equivalent or essentially identical in their music-theoretical significance. In assuming octave but not enharmonic equivalence, he prefigures the later concept of tonal pitch classes (Temperley, 2000) that we also adopt here. His rendition of tone relations is reproduced in Fig. 2 as a particularly elaborate example of the Tonnetz.

Fig. 2: The Tonnetz by Hostinský (1879, 67) using the German convention for pitch-spelling.
figure 2

Lines above or below pitch names indicate syntonic comma differences.

Full size image

In contrast to Euler’s earlier graph, Hostinský’s Tonnetz extends infinitely in all directions. Moreover, while the minor third does, following Hauptmann, not constitute one of the primary intervals, the hexagonal structure and symmetries in Hostinský’s Tonnetz allow one to endow all three primary intervals with equal status—although he remarks that the degree of familiarity is highest for perfect fifths and lowest for minor thirds. Hostinský shares Hauptmann’s assessment of the role of the primary intervals, but more explicitly extends it with a notion of compositionality: tones are “directly related” if they share an edge on his version of the Tonnetz, i.e., if they are related by either a perfect fifth, a major third, or a minor third. Thus, each tone on the Tonnetz is directly related to its neighbors by one of the primary intervals, and indirectly by combinations of those to all other tones. Hostinský’s model of tonal relations thus anticipates later formalizations and usage of the Tonnetz in mathematical and computational music theory (e.g., Bernardes et al., 2016; Cohn, 1997; Harrison and Pearce, 2020; Lewin, 1987; Longuet-Higgins, 1987; Mazzola, 1990; Navarro-Cáceres et al., 2020; Purwins et al., 2007; Rohrmeier and Moss, 2021; Tymoczko, 2012).

Building on the above considerations and the music-theoretical concept of the Tonnetz, Lieck et al. (2020) have proposed the Tonal Diffusion Model (TDM), which takes as input the frequencies of occurrence of pitch classes in a piece of music. It then estimates the piece’s tonal center as well as the most likely distribution of primary intervals to generate all tonal pitch classes in the piece by “diffusing” them trough paths on the Tonnetz starting from that tonal center (for details, see “The tonal diffusion model”). In their initial analysis of three corpora of pieces by Bach, Beethoven, and Liszt, the authors used their model to find differences between the composers’ styles, and showed that the former two compose largely within a diatonic tonal framework but the latter employs harmonies drawn from the extended tonal idiom, confirming prior theoretical work (Baker, 1990; Forte, 1987; Polth, 2018; Rohrmeier, 2020; Schild, 2010; Schoenberg, 1969).

While this study focuses on music-theoretical and computational work, questions surrounding the perception of intervals and tonality have received substantial attention in music psychology, especially regarding consonance and dissonance (Harrison and Pearce, 2020; Popescu et al., 2019). For a recent comprehensive review of the psychoacoustic foundations, see Parncutt (2024).

Research questions

Musicological and music-theoretical accounts as well as the empirical studies in computational musicology and music information retrieval discussed above account for the fact that harmony undergoes substantial historical changes. These studies observe, for instance, that composers in different periods favor different combinations of tones or harmonies, or that they use different syntactical approaches to combine basic musical elements to weave a piece’s fabric. In the present study, we apply the Tonal Diffusion Model to a corpus spanning a wide historical range of approximately 600 years. We are mainly interested in how stylistic changes manifest themselves in the interval structure of musical pieces, and the extent to which they can be corroborated by a computational model of tonal space. The overarching goal of this study is to inquire how changes in the prevalence of the primary intervals relate to the history of tonality. More specifically, we ask the following research questions:

  1. (1)

    Can we observe a historical trend in the exploration of tonal space?

  2. (2)

    What is the relative importance of the primary intervals, and how do they vary over time?

In what follows, we first briefly introduce the corpus as well as the computational model (“Methods”) that we use here. We then proceed to present our results (“Results and discussion”) and relate them to our research aims. We conclude by discussing how computational modeling can benefit historical and theoretical work on music, of which we conceive our contribution to be an example.

Methods

Data

Large diachronic corpora suitable for computational music research are rare. One of the few existing examples is the so-called Yale Classical Archives Corpus (YCAC; White and Quinn, 2016),Footnote 3 a dataset that was assembled by scraping MIDI files from the community-driven website Classical ArchivesFootnote 4 and extracting a number of features from it that are of music-theoretical interest. While it constitutes one of the largest corpora available for computational historical music research, it has two problematic shortcomings: first, since the data is drawn from MIDI files, information about pitch-spelling is ambiguous (i.e., it is not straightforward to determine which enharmonic spelling should be chosen, and different pitch-spelling algorithms can potentially lead to different results). Second, the data quality is highly uncertain since it was created by online users of the website without any further scholarly critical assertion or editing.Footnote 5 That being said, it is a useful resource for many applications in computational musicology but could not be used for our present purposes. Authors of the diachronical studies reviewed above have mostly used a strategy of manually compiling datasets from various resources for their studies.

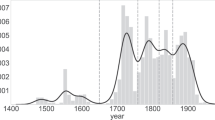
Here, we employ the Tonal Pitch-Class Counts Corpus (TP3C; Moss et al., 2020a). While this dataset does not claim to be a representative sample of Western art music, it does to some extent represent the current state-of-the-art in digital musicology as it draws on and combines multiple openly available resources, and supplements them with a number of other pieces (Moss, 2019). One could call this a ‘consensus strategy’. The diverse symbolic music encoding formats have been converted to MusicXML (Good, 2013), one of the most widely used formats in both commercial and open-source music notation softwares. The TP3C consists of 2,012 pieces by 75 composers over a range of about 600 years. More specifically, it only contains the tonal pitch-class counts found in these compositions. Each piece in the corpus is represented as a 35-dimensional vector spanning pitch classes F♭♭ to B♯♯ in line-of-fifths ordering (Moss et al., 2023). A temporal histogram of pieces in the corpus is shown in Fig. 3.

Fig. 3
figure 3

Histogram of the distribution of pieces in the Tonal Pitch-Class Counts Corpus (TP3C).

Full size image

An important caveat needs mentioning. Historical datasets are frequently not balanced. Different numbers of pieces have been produced in different periods, composers’ creative output has varied under different historical and cultural conditions. Moreover, diverse genres, instruments, or functional contexts have been employed, rendering diachronic music corpora far from being systematically sampled, which is a common characteristic of observational studies more generally (Rosenbaum, 2010). On top of the factual imbalance of historical data, there are several forms of biases that affect their assemblage: what is being digitally encoded is frequently affected by personal tastes and preferences (e.g., by the Classical Archive users) or by scholarly traditions within musicology that tend to perpetuate canonical repertoires (as in the case of the TP3C). We believe, however, that these caveats do not fundamentally impede large-scale quantitative analyses of historical music data. They rather emphasize the need to bear these shortcomings in mind when interpreting the results, and to draw attention to further broadening the musicological canon, e.g., also by including formerly less frequently studied composers (e.g., Hoag, 2022).Footnote 6

The tonal diffusion model

Music-theoretical models of tonal space are most commonly understood as models of abstract musical relationships, e.g., maps of key or tonal relations, rather than models of how these relations manifest themselves in works of music. They represent the map, not the journey. In order to bring these two perspectives together, it is necessary to build models that are both formally precise and can be applied to actual musical corpora.

As an example of such a formalization, Lieck et al. (2020) have proposed the Tonal Diffusion Model (TDM) that bridges the gap between formal modeling, data-driven inference, and music theory. Internally, it represents pieces of music as distributions of tonal pitch classes and fully describes the generative process for these tones. It incorporates the music-theoretically motivated assumption that each piece possesses a tonal center, that is, a particularly distinguished note that often, but not always, closes or opens a composition, and that is relatively frequent throughout the course of a piece. All other tones are explained as originating from this central tone through a “diffusion” process (a path or sequence of steps) along the major axes of the Tonnetz, the so-called primary intervals. Recall that these are the ascending and descending perfect fifth (+P5/−P5), major third (+M3/−M3), and minor third (+m3/−m3). They are shown schematically in Fig. 4 with the tonal center set to pitch class C. The main difference to Hostinský’s Tonnetz (Fig. 2) is that the TDM distinguishes also between intervallic directions (ascending or descending).

Fig. 4: Section of the Tonnetz, centered on pitch class C.
figure 4

Arrows indicate directed primary intervals.

Full size image

Concatenating primary intervals to paths on the Tonnetz allows one to trace back those paths from any given pitch class to the tonal center of a piece. Since there are many, indeed infinitely many, different paths connecting two tones on the Tonnetz, the model considers all possible paths with a preference for shorter paths. The overall probability of a pitch class then is the marginal probability over all possible diffusion paths.

The direction in which pitch classes tend to diffuse from the tonal center is controlled by interval weights for the six primary intervals. The preference for shorter paths is governed by a diffusion parameter that controls how far pitch classes tend to diffuse from the tonal center. In other words, it determines the probability of how many steps are needed to trace back a tonal pitch class to the tonal center of the piece. The higher the value of the diffusion parameter, the greater the probability for longer paths and thus more complex interval relations between a tone and the tonal center of a piece.

The generative process of the TDM

Structurally, the TDM is comparable to a topic model (Blei, 2012). To illustrate how the model works, we now briefly describe the generative process for a piece of music as defined by the model. A more detailed description and discussion is given in Lieck et al. (2020).

Each piece in a corpus D is represented as a bag (multiset) of tones t, which are assumed to be independently generated. The generation of a piece starts by drawing a tonal center c from a prior distribution over all possible tonal centers (Eq. (1)). In general, this prior distribution is defined by a Dirichlet process with base distribution Hc and concentration parameter αc. Hc can be used to make some tonal centers (e.g., those with fewer accidentals) more likely than others, but it is chosen to be uniform to have a neural prior.Footnote 7 The second step is to draw an interval weight distribution w. Again, the prior distribution is defined by a Dirichlet process with parameters Hw and αw that is chosen uniform to be neural (Eq. (2)). Finally, a diffusion parameter λ is drawn from a suitable prior distribution with parameters hλ (Eq. (3)). p defines a distribution over diffusion path lengths (e.g., Poisson or binomial) and the prior is again chosen to be uniform. Together, c, w, and λ define how tones in this particular piece are generated, as follows.

Each observed tone t in the piece is generated by first drawing a path length n (the number of diffusion steps; Eq. (4)). Then, a sequence of latent tones τ0, . . . , τn is generated by starting at the tonal center τ0 = c (Eq. (5)) and repeatedly (n times) selecting a primary interval according to their weights w and taking a step on the Tonnetz in that direction (Eq. (6)). The last latent tone (τn) in this sequence is the outcome of the generative process, i.e., the observed tone t (Eq. (7)). The following equations summarize and fully specify this generative process defined by the TDM:

$$c \sim {{{\rm{Dirichlet}}}}({H}_{c},{\alpha }_{c}),$$
(1)
$$w \sim {{{\rm{Dirichlet}}}}({H}_{w},{\alpha }_{w}),$$
(2)
$$\lambda \sim p(\lambda \,| \,{h}_{\lambda })$$
(3)
$$n \sim {{{\rm{PathLength}}}}(\lambda )$$
(4)
$${\tau }^{0} \sim {{{\rm{Categorical}}}}(c)$$
(5)
$${\tau }^{i+1} \sim {\tau }^{i}+{{{\rm{Categorical}}}}(w)$$
(6)
$$t\leftarrow {\tau }^{n}.$$
(7)

The bag-of-notes assumption of the TDM means that tones are considered to be independent of one another and only the overall probability p(t∣c, w, λ) of generating a tone t (conditional on the piece-specific parameters c, w, and λ) needs to be considered. This probability is computed by marginalizing ("averaging”) over all possible paths from the tonal center c to the tone t using dynamic programming. Inferring the most likely parameters for a given piece then corresponds to optimizing c, w, and λ so that the predicted pitch-class distribution best matches the observed one.Footnote 8 This is described in more detail in Lieck et al. (2020).

Locally weighted scatterplot smoothing with bootstrapping

In order to trace historical changes in the distribution of the inferred parameters, we use Locally Weighted Scatterplot Smoothing (LOWESS; Cleveland and Devlin, 1988) and its Python implementation in the statsmodels library (Seabold and Perktold, 2010). This method fits a local polynomial regression to only a neighborhood of each data point rather than to the entire dataset. For a given dataset of N points (xi, yi), the LOWESS model estimates a value \({\tilde{y}}_{i}=f({x}_{i})\) for some smooth function f by taking only the ⌊δN⌋ points closest to xi into account, with a fraction parameter δ ∈ (0, 1). It then performs a weighted linear regression with some weighting function.Footnote 9 The larger the fraction of data taken into account, the smoother the resulting LOWESS curve. For all our analyses below, the fraction parameter was set to δ = . 3 in order to achieve a reasonably smooth result. Note that the local environment is defined as an integer fraction of the size of the dataset, that is, in terms of the number of data points. Distances between them, in our case measured in years, are only used in the weighting function. This means that different neighborhoods always take the same number of pieces of music into account but may span varying year ranges. In periods with fewer pieces, a larger time range will be taken into account and vice versa. Corpora of pieces of music will, in general, be distributed non-uniformly across the historical timeline. First of all, because different times have produced varying numbers of compositions, affected, e.g., by technical innovations or preservation strategies. Secondly, since corpora are usually constructed with a certain purpose in mind (Piotrowski, 2019) they are, by definition, biased. Corpus construction thus directly influences the smoothness of LOWESS curves, which is why we always display them along with the original unaltered data points in our results below.

The procedure just described yields exactly one smooth curve for a given dataset. In order to get a better understanding of the variance within the data, we apply the LOWESS method not to the entire corpus D, but to a set of so-called bootstrap samples D(1), …, D(B). Bootstrap sampling is an established method for estimating uncertainty (Hastie et al., 2008). A bootstrap sample D(b) is obtained from D by drawing N = ∣D∣ pieces from it with replacement. For the results below, we set B = 250.

Operationalizations

Now that we have introduced the generative process of the Tonal Diffusion Model, we are able to relate our research questions (“Research questions”) to the inferred values of the model’s parameters when confronted with pieces in the corpus.

  1. (1)

    Can we observe a historical trend in the exploration of tonal space? We measure this as changes in the strength of the diffusion parameter λ.

  2. (2)

    What is the relative importance of the primary intervals and how do they vary over time? This is measured by the distributions of relative frequencies of the primary intervals.

Results and discussion

By applying the Tonal Diffusion Model to the TP3C, we are able to infer a set of six primary interval parameters (see Fig. 4) and one diffusion parameter for each piece in the corpus. In other words, for a given piece in the corpus, the TDM finds an optimal parameter setting θd that best explains the distribution of tonal pitch classes in this piece according to the model’s assumptions (in particular, that tonal relations are constituted solely via concatentation of the primary intervals). We then use the temporal distribution of these parameter values in order to find answers to our three research questions laid out in the introduction. In order to interpret our results correctly, it is important to recall that the weights of the six primary intervals are not independent of one another: for each piece, they form a six-dimensional probability vector summing to one.

Below, we study the temporal changes of the diffusion parameter and analyze the distributions of the six weight parameters across time. While visible changes in the plots below nearly coincide with boundaries between centuries, this bears, of course, no importance for their interpretation, in particular since historical periods do not strictly follow a steady rhythm. We only include the vertical lines indicating centuries to ease orientation.

Tonal interval relations become increasingly complex

We first analyze the collection of diffusion parameters λ because it will be informative as to whether there is an observable historical trend. Since this parameter is independent of the six interval weight parameters, we can discuss it separately. The historical distribution of the diffusion parameter is shown in Fig. 5. Each gray ‘ × ’ corresponds to the diffusion parameter of a particular piece in the corpus. In addition, 250 LOWESS curves are shown in green, each estimated based on a bootstrap sample of the complete corpus. Taken together, this renders a full picture of both the historical distribution of the path lengths as well as its long-term diachronic trends.

Fig. 5
figure 5

Historical diffusion parameter distribution with LOWESS curves (green lines) fitted to 250 bootstrap samples.

Full size image

In general, the LOWESS curves generated via bootstrapping have a low variance, indicating that the average diffusion strength λ can be reliably estimated from the data. Moreover, the curves remain within a relatively narrow interval of λ ∈ (. 8, . 9). This restricted range means that, overall, we do not observe drastic changes in the average spread of tones around the tonal center, although individual pieces may strongly deviate from this average value as is clearly visible in Fig. 5. At the same time, there is a clear trend within this range: in the first four centuries, until approximately the end of the 17th century, one can observe an almost linearly increasing trend, corresponding to a monotonous growth of average path lengths. In both the 18th and the 19th centuries, the trendlines exhibit local maxima towards the midpoint of the two centuries, although the trendlines do not fall back to previous lower values and thus maintain the generally rising trend.

The bundled LOWESS curves show a remarkable resemblance to the ones reported in Moss et al. (2023). There, the local regressions were performed over the fifths width, the minimal span containing all tonal pitch classes on the line-of-fifths for a given piece of music.Footnote 10 The two measures (fifth width and inferred diffusion strength) are moderately positively correlated (Pearson r ≈ . 254), and increasing diffusion strength by a factor of .1 corresponds, on average, to an increase of about 1.54 fifths (see Fig. 6). The diachronically growing values of the diffusion parameter express that the TDM’s derivations of pairwise tonal relations along the axes of the Tonnetz become increasingly complex, that is, they tend to involve ever more derivation steps and simpler, e.g., direct explanations become less frequent.

Fig. 6
figure 6

Positive correlation between the discrete fifth width (x axis) and continuous diffusion strength (y axis).

Full size image

Perfect fifths dominate pitch-class distributions for centuries

Paths on the Tonnetz tend to get longer throughout the historical time frame under consideration. Now, we analyze the components from which these paths are constructed, namely the distributions of the weights of the six primary intervals, shown in Fig. 7. Each panel shows the weights of one primary interval for each piece in the corpus (gray ‘+’ signs). The top row shows ascending, and the bottom row shows descending intervals. Perfect fifths are shown in the leftmost column, and major and minor thirds are shown in the middle and right columns, respectively. The colored lines correspond to LOWESS curves fitted to 250 bootstrap samples from the corpus.

Fig. 7: Historical distribution of primary interval weights inferred with the TDM.
figure 7

Gray plus signs show inferred interval weights and colored lines show LOWESS curves of 250 bootstrap samples.

Full size image

Looking at these distributions, a clear narrative emerges. From the late 14th to the late 17th century, the interval of the perfect fifth, both ascending and descending, overwhelmingly dominates the distributions of primary intervals, resulting in the virtual non-existence of the minor and major thirds as steps on the Tonnetz to relate the tones in a piece of music to its tonal center. Perfect fifths truly emerge here as the fundamental interval for Western classical music under this model.

Importantly, this means that during this period, the most parsimonious explanation for minor or major thirds is, according to the TDM, in terms of a sequence of three or four fifth steps, respectively, rather than by a single, direct step. This may seem counterintuitive at first because a single step seems more parsimonious than three or four steps. It becomes clear when considering that we do not only have to explain what we do see in the data but also what we do not see. In particular, resorting to ad hoc explanations for individual cases (direct steps) begs the question of why this is not observed more frequently in general. For instance, if we assume one minor-third step on the Tonnetz likely to occur, we should also expect two consecutive minor third steps (a diminished fifth or, enharmonically equivalent, a tritone) to be relatively frequent in the data. In contrast, if many observations require ‘wandering around the line of fifths’ to be explained, observing a minor or major third does not require additional, separate explanation. Thus, not assuming a direct step is the more parsimonious explanation in this case. Note, nonetheless, that individual pieces may have significantly higher weights especially for minor thirds (up to ~0.2/0.4 for ascending/descending minor thirds), indicating that in these individual cases, assuming direct steps better explains the data. In other words, while there are numerous examples in our corpus for which minor- or major-third relations play a significant role, the overall trend emphasizes the much higher importance of ascending and descending perfect fifths.

Within the time span up to the late 17th century, one can observe a modest but stable increase of ascending perfect fifths at the expense of descending ones. In other words, the model increasingly interprets tones as being related to the tonal center by ascending from the tonal center to the respective tones via perfect fifths, corresponding to a higher frequency of rightward motions from the tonal center (see Fig. 4). This is equivalent to saying that tonal centers lie increasingly ‘lower’, or flatwards, on the line-of-fifths, and the remaining tones of the piece are increasingly in sharpward direction. This preference for ascending fifths is present from the beginning but further increases over time. While our model cannot make any causal claims, it is tempting to see herein a reflection of the increasing directedness that is a result of the transition from modal to tonal music, where the latter exhibits a preference for authentic, falling fifths as the fundamental harmonic motion, e.g., of chords and modulations, as opposed to favoring plagal motions of ascending fifths. This finding corroborates the irreversibility reported by González-Espinoza et al. (2020) and the asymmetry found by Moss et al. (2019).

In contrast to the period until the late 17th century, during the 18th century, roughly corresponding to music in the Galant style (Gjerdingen, 2007), this trend is drastically reversed. A striking rise of descending perfect fifths can be observed, at the cost of ascending ones. This new preference for descending fifths almost surpasses pre-1400 levels to reach its highest point throughout the entire time span under consideration so far (the late 1300s to the end of the 18th century). While we had observed an almost constant rise of ascending perfect fifths (corresponding to authentic relations to the tonal center), we witness a renewed stronger disposition of descending perfect fifths during the 18th century, corresponding to a more balanced proportion of authentic and plagal motions on average (Weiß et al., 2019).

A sudden rise of thirds in the 19th century coincides with the emergence of extended tonality

In comparison to the fifths, both the minor and major-third parameters do not play a significant role in the first four centuries. While there are a few non-zero weights for the two third intervals, they are dwarfed by the strength of the ascending and descending fifths. This can be seen by the scattered crosses in the corresponding subplots in Fig. 7: the trend lines for the thirds are ‘pulled down’ by the overwhelming proportion of zero values, a direct consequence of the surpassing presence of perfect fifths. This does, however, not entail that thirds are not important for tonal music. It rather means that the model explains the occurring thirds in terms of fifths relations instead of assuming a separate dimension for thirds. For instance, instead of explaining the motion from C to E with a single step in the direction of an ascending major third, the model seems to prefer, so far, to explain the relation between the two tones by ascending from C via G, D, and A, to E in a sequence of ascending perfect fifths—which makes sense in contexts of heavily used diatonic sets.

Against the backdrop of the previous findings, it is noteworthy that major and minor thirds gain substantial weight at all. Even more so, they become sufficiently strong to visibly affect the relative prominence of perfect-fifth weights during the 19th century, as can be clearly seen in the leftmost column of Fig. 7. This holds true for ascending major thirds as well as descending minor and major thirds, and to a lesser extent also for descending major thirds. It appears that the tonal pitch-class distributions of the 19th-century compositions in the corpus are shaped in such a way that third-based explanations are much more likely than in earlier centuries. While the absolute strengths of the thirds as compared to the perfect fifths are still vanishingly small, their relative magnitudes in the 19th century as compared to earlier periods are much greater (see Fig. 8). The model does pick something up in the pitch-class distributions of 19th-century compositions that had not been there in previous centuries. This is in strong correspondence with virtually all theoretical accounts of harmony and tonality in the 19th century, e.g., Fétis (1844); Hauptmann (1853), to name just two prominent examples. It also resonates with modern neo-Riemannian approaches (Capuzzo, 2004; Cohn, 2012; Harasim et al., 2019; Lehman, 2018; Moss, 2024) and recent work on Tonfeld theory (Polth, 2018; Rohrmeier and Moss, 2021), in which the thirds—both major and minor—occupy a center-stage role. Moreover, it aligns well with the more recent results of Yust (2019) who finds diminishing usage of diatonic, i.e., fifths-based, pitch-class sets in the 18th and 19th centuries (corresponding to an increase of third-based sets).

Fig. 8: Historical distribution of primary interval weights inferred with the TDM, zoomed in.
figure 8

Gray plus signs show inferred interval weights and colored lines show LOWESS curves of 250 bootstrap samples. Note that y-axes of the subplots are commensurate, and the trend lines for both the ascending and descending perfect fifths lie therefore outside the depicted range.

Full size image

The absolute values of the parameter weights are weakest for the major thirds, both ascending (+M3) and descending (−M3). This somewhat stands in contrast to Hostinský’s assessment of the relative importance of the primary intervals, concluding that “the degree of relationship is strongest in the fifth direction, and weakest in the minor third direction” (Hostinský, 1879, 67). While our results seem to contradict this assessment, one has to bear in mind that Hostinský’s account is based on theoretical considerations and ours on empirical investigation. Whilst one cannot directly equate the theoretician’s assessment of intervallic importance with pitch-class frequency counts, one would assume that there is at least some correlation between the two, and our findings appear to falsify Hostinskýs claim in that respect. One has to bear in mind, however, that Hostinský and most of his contemporaries deduce intervallic importance from the harmonic series, which is, of course, unaffected by frequencies of occurrence of pitch classes in musical corpora. Another reason for the observed discrepancy might be the mere fact that combinations of major thirds (e.g., augmented fifths) require a change of key or modal mixture, thus a more complex tonal relationship. Because those are substantially rarer than tritones, the TDM explains major thirds on average more likely to be produced by a sequence of four perfect fifths. Most importantly, Hostinský’s “degree of relationship” needs not necessarily coincide with our frequency-based measure of the primary intervals and, thus, our results should not be construed as rejecting the theorist’s judgment of intervallic importance. Clarifying the relation of axiomatically defined tonal relations and derived interval relations to empirically observed distributions of tones and inferred interval relations remains a challenging field of research.

It is interesting that the peak of the model’s third-based explanations for tonal interval relations is about at the middle of the 19th century, after which they tend to decrease again. This decrease, however, is conditioned on the historical extent of the corpus we used, since the bootstrapped LOWESS curves are heavily affected by the lack of data towards the end of the historical time frame investigated here (see Fig. 3). Thus, whether and how the trend continues into the 20th century remains to be investigated in future research.

General discussion

We have shown how computational modeling can be used for musicological inquiries. Specifically, we demonstrated how formalization and computational implementation of music-theoretical conceptualizations of tonal space allow for drawing inferences about historical developments when applied to a large corpus of music. Our main research question was whether it is possible to observe trends in the exploration of tonal space across the historical timeline. While it is to be expected that any measure taken over a sufficiently large diachronical frame is bound to change, our results here have shown that it is possible to speak of a “trend”, that is, a consistent pattern of change (Raulo et al., 2023), clearly indicating a growing usage of tonal pitch classes more remote from the tonal center, which is in line with stylistic changes due to increasing chromaticism and enharmonicism (Cohn, 2012). Future work needs to consider how these stylistic changes can be incorporated into computational models, e.g., as latent variables in a hierarchical generative setting.

Since our model is fundamentally about intervallic relations, our second research question concerned the mutual importance of the so-called primary intervals (perfect fifths, major thirds, and minor thirds, each in ascending and descending direction), and whether changes in their relative prominence manifest themselves as trends as well. Again, observing no changes at all would run contrary to our expectations based on the historiography of Western music, but our interest was to trace the exact nature of interval variation. As we have shown, the presence of thirds (both major and minor) is negligible when compared absolutely to the overwhelming dominance of perfect fifths. Their relative frequencies, however, show a striking pattern of rise and fall in the 19th century. This result, moreover, emphasizes that the two perspectives of absolute and relative frequencies of occurrence benefit music-theoretical considerations, and we believe that corpus studies provide methodological advantages over manual music analysis in this regard.

Conclusion

In summary, the results of our study are all well-supported by prior literature in music theory and historiography as well as several recent computational studies on the history of tonality reviewed in the Introduction. Apart from the specific results reported in this study, we moreover demonstrate that interdisciplinary work between humanistic and scientific approaches to the study of music can be fruitful. While the model we used is relatively simple and operates only on a limited representation of pieces of music, namely their pitch-class counts, its restricted complexity renders its inferences interpretable and thus informative from a musicological point of view. It moreover provides clear interfaces to existing historical models and conceptualizations.

A major limitation, however, lies in the largely observational nature of the results. While we argue, for instance, that the stark increase of thirds in the 19th century corroborates the research literature on the rise of extended tonality in that era, we cannot make any claims as to why this is happening based on our model and the available data alone. To do so would indeed require both more sophisticated models as well as the inclusion of richer data, including meta- and paradata. We thus hope that our study initiates deeper conversations about computational modeling for musicology, in particular within historical research contexts.

We believe that there is a need for well-crafted computational models that, on the one hand, take into account the intricate nature of structural components of music, such as tones, intervals, chords, harmony etc. as well as their interactions. On the other hand, future research should work towards historically informed models of the transmission mechanisms themselves that would allow researchers to transcend beyond the observational state of many of the studies reviewed in the introduction. Whilst their application to the history of Western art music is still in its infancy, researchers in the field of cultural evolution have begun to adapt quantitative models in other musical scenarios, e.g., electronic music (Youngblood, 2019), pop (Singh and Nakamura, 2022), medieval chant (Nakamura et al., 2023), and folk song (Street et al., 2022), and this seems to be a promising avenue for future research.