Introduction

Throughout the Nineteenth century, the so-called “common practice” of Western classical music—the prevalent musical style that had characterised the previous decades—underwent major stylistic changes (Dahlhaus 1989; Kramer 1981; Schönberg, 1975). By the beginning of the new century, a deeply transformed musical landscape had formed, including “extended” forms of tonality (Cohn 2012; Horton 1998), musical impressionism (Byrnside 1980) and, eventually, atonality (Forte 1973). These transformations were introduced as part of the stylistic experimentation of many individual composers, and it is a challenge for musicological research to trace such historical development in specific features of their compositions. In this paper, we propose a corpus-based approach to investigate the emergence of stylistic novelty at the turn of the Twentieth century by the example of the French composer Claude Debussy (1862–1918).

Debussy is widely considered among the most original and innovative composers of his time (Trezise 2003), yet traits of the earlier common-practice diatonic tonality are not extraneous to his works: for example, the tonic-dominant polarity is omnipresent in the composer’s music (Novak 2015; Elder 1988; Ottman 1984; Pomeroy 2003). However, the goal-directed nature of tonal harmony is often found to be weakened as harmonies are not primarily structured according to their tonal function, serving colouristic and textural purposes instead (Giannetta 2007; Pomeroy 2003; Schönberg 1975). Furthermore, while common-practice music is—conceptually, at least—primarily based on diatonic scales, Debussy exploits a harmonic palette in which diatonic chord forms are blended with or replaced by octatonic, whole-tone, or other chromatic structures (Tobin 2002), often fluctuating between several different pitch-class sets (or Tonfeld structures, see Polth 2011, 2018). Overall, compared to the earlier common-practice, Debussy’s tonality is instantiated more ambiguously, yet remains capable of expressing coherence in the use of pitch-class materials.

Music-analytical approaches suggest that these aspects of the composer’s characteristic mature style underwent an evolution, in particular with respect to the interaction between traits inherited by the earlier common-practice and his own stylistic explorations. For example, whole tone, chromatic, and octatonic procedures are more prominently associated with later works, leading towards a new paradigm that has been characterised as expressing weakened directionality, ambiguous tonal organisation (Salzman 2002), and an equalisation of the twelve tones (Tobin 2002). However, a comprehensive characterisation of diachronic trends with respect to specific and well-defined compositional features is still to be achieved. As a contribution in this direction, the aim of this paper is to investigate with corpus-based quantitative methods the emergence of some distinctive features of Debussy’s mature style across the composer’s œuvre for solo piano. In the following, we first identify specific features that contribute to tonal ambiguity and coherence as relevant to characterise Debussy’s style. In particular, we propose that the use of symmetric pitch-class materials (Section “Symmetry and tonal ambiguity”) and the coexistence of multiple pitch-class materials in the same piece (Section “Fragmentation as the coexistence of multiple pitch-class structures”) are markers of tonal ambiguity, while the prevalence of individual pitch-class materials over large timespans within a piece (Section “Global prototypicality as a form of coherence”) is a marker of compositional coherence. We then propose a computational approach for tracking their diachronic development by means of hierarchical representations based on the Discrete Fourier Transform (Amiot 2016).

Symmetry and tonal ambiguity

The musical system of major/minor tonality inherits many properties from the asymmetry properties of the diatonic scale as a subset of the chromatic set (Amiot 2007). For example, in a major scale, the asymmetric (yet maximally-even) positioning of the semitones between scale degrees 3–4 and 7–8 provides reference points for orientation in pitch-class space (Clough and Douthett 1991; Harasim et al. 2020). In general, asymmetry or moderate degrees of symmetry in musical scales allow for the uniqueness property, whereby each scale degree is characterised by a unique network of intervallic relationships with all other scale degrees (Balzano 1982). In the perception of diatonic tonality as a coherent “system of tonal relations”, this property contributes to identifying each scale degree through its unique function, in terms of a specific tendency to move towards other scale degrees (Butler 1989; Butler and Brown 1984). Differently from the diatonic scale, symmetric pitch collections do not share the uniqueness property. Among these, particularly important in Western classical music are pitch collections with rotational symmetry, or modes of limited transposition (Messiaen 1944), as well as those with uniform symmetry, characterised by equal divisions of the octave in minor-third (diminished tetrads), major-third (augmented triads), or whole-tone (whole-tone scales) steps.

More generally, asymmetric scales are found cross-culturally as a statistical universal of music making (Savage et al. 2015). Asymmetry is associated with cognitive advantages that contribute to perceiving the tonal system as a coherent musical system. For example, while diatonic tonality is associated with a clear tonal hierarchy that is reflected in perception (Krumhansl and Kessler 1982), the perceptual pitch profiles primed by a symmetric collection such as the octatonic scale fail to engender a clear perceptual hierarchy (Krumhansl and Schmuckler 1986). Additionally, implicit learning of statistical properties in artificial musical systems, such as tonal hierarchies and expected melodic motions, is facilitated when the underlying scale is endowed with the uniqueness property, as opposed to symmetric scales that do not share such property (Pelofi and Farbood 2021). Since infants’ pitch perception is more accurate when pitches are drawn from asymmetric scales than from symmetric scales, these cognitive advantages may be to some extent innate and universal (Trehub et al. 1999).

Overall, using symmetric scales does not only represent a departure from the diatonic system per se: it also leads to renouncing the property of uniqueness, which guarantees orientation in pitch space and well-defined tonal functions, as well as the cognitive advantages in acquiring the syntactic make-up of an asymmetric pitch organisation. A musical system based on an extensive use of symmetric pitch-space structures is then not only more likely to be unfamiliar to the ears of a tonally-enculturated listener, but also potentially more elusive to cognitive appraisal, overall inducing a more ambiguous listening experience. Since such ambiguity is characteristic of Debussy’s compositional style, the development of the latter may have been partially achieved by means of an increase in the prominence of symmetric pitch collections relative to that of (asymmetric) diatonic ones, as is suggested by analytical close-readings (Forte 1991; Parks 1980; Tobin 2002).

Fragmentation as the coexistence of multiple pitch-class structures

Traditional theories of Western common-practice tonality regard the diatonic system as the sole type of pitch-space organisation underlying tonal structure: in this view, chromaticism either constitutes a separate musical system to be considered “other” from classical tonality (Proctor 1978), or arises through mixtures and tonicisations within the diatonic system (Brown 1986). The reliance on a single type of structure in pitch-space, the diatonic one, ensures that, in a typical tonal piece, hierarchy and functions of diatonic scale degrees are preserved across the entire piece, guaranteeing coherence at the large scale. Furthermore, different instantiations of the diatonic system itself govern the piece recursively at different time-scales, ensuring coherence across time-scales (Rohrmeier 2011).

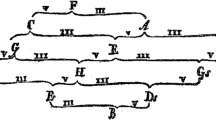
On the contrary, Debussy’s later compositions have been acknowledged to demonstrate a “more refractory than ever approach to syntactic continuity of harmonic practice” (Pomeroy 2003, p. 156). Among the features that contribute to this apparent discontinuity is that different types of pitch materials (beyond the diatonic scale) may be foregrounded in different segments of a piece. Debussy’s practice of blurring or replacing diatonic structuring principles might be illustrated through the example of Ondine from the second book of Préludes, L. 131, no. 8. This piece has been analysed as marking “one of Debussy’s most extreme essays in discontinuity” (Wheeldon 2004), based on its reliance on gestures and motivic cells rather than themes. These cells display disparate pitch collections and are frequently juxtaposed with little continuity other than bass pedal points supporting longer passages. Some sections of the prelude are outside of the alleged overarching tonal centre D and therefore seemingly autonomous, with harmonic stasis often reinforced by motivic circularity (Wheeldon 2004).Footnote 1 As exemplified by the analysis in Fig. 1, the music moves through various types of (diatonic and non-diatonic) pitch structures, and functional relationships become subordinate to new interactions between pitch sets. The traditional continuity of hierarchies and functional relations of individual diatonic tones are then lost, or at least harder to track, over the timescale of the entire piece. We term “degree of fragmentation” the degree to which several different pitch-structures govern a piece at different timescales, and we set out to test whether the departure from (unitary) diatonic structure may also be reflected by a progressive increase in fragmentation throughout Debussy’s life.

Fig. 1: Gradual transformation of pitch sets in Ondine, mm 37–44ff.
figure 1

The transformations, here, are mostly based on downward shifts in semitones and proceed from a passage based on the whole-tone scale (m. 37) over an Eb lydian collection (m. 38 f.), a more indeterminate sonority (m. 40 f.), and a chromatic theme (m. 42), to the octatonic segments from m. 44 onwards. For the segment mm. 44ff. we have changed the pitch spelling to sharps to reflect the one in the score.

Full size image

Global prototypicality as a form of coherence

As discussed above, diatonicity governs the pitch-class content of tonal pieces both locally at small time scales as well as globally at the time scale of the entire piece (Rohrmeier 2011; Lieck and Rohrmeier 2020; Sapp 2001; Viaccoz et al. 2022). The idea that large segments of a piece, up to the entire piece as a whole, globally manifest a single prototype of pitch-class materials can then be seen as one of the factors guaranteeing global coherence to tonal pieces, that we term global prototypicality. This form of coherence, whereby the variety or complexity in a piece originates from a “selectivity and economy of pitch resources” (Parks 1980, p. 120), has been suggested as a feature of Debussy’s idiom as well. However, if Debussy’s pieces did become increasingly fragmented over time as hypothesised in the previous Section “Fragmentation as the coexistence of multiple pitch-class structures”, did they also lose such global coherence? As segments expressing different prototypes such as diatonic, hexatonic, or octatonic pitch-class collections are combined to form larger and larger sections of the piece, it is possible that no individual prototype would prevail at larger timescales, thus decreasing the degree of global prototypicality. Based on this perspective, we then also sought to test whether any diachronic trend relative to fragmentation is associated with a corresponding opposite trend in the degree of global prototypicality.

Discrete fourier transform and wavescapes

Investigating types of pitch-class materials in an empirical corpus study requires a computational approach that is both scalable to a large corpus, and music-theoretically interpretable. A mathematical tool that is naturally apt for investigating pitch collections with different symmetry properties is the Discrete Fourier Transform (DFT). The pitch-class content of any region of a piece can be represented as a distribution of pitch classes, i.e., the aggregated duration of each pitch class occurring in that region. Under DFT, such a distribution is decomposed into a mixture of distinct components. Each component resonates with a specific prototype of music-theoretically relevant pitch-class structures (Amiot 2016): the 1st component is interpreted as an indicator of “chromaticity”, the 2nd component is associated with the presence of a salient tritone (“tritonicity”), the 3rd with an augmented triad (“augmentedness”), the 4th with a diminished triad or octatonic collection (“octatonicity”), the 5th with a diatonic collection (“diatonicity”), the 6th with a whole-tone scale (“whole-toneness”). While the prototypes for components 1, 2, 3, 4, and 6 coincide with symmetric collections, the 5th coefficient resonates instead with asymmetric diatonic or pentatonic collections. Overall, given a pitch-class distribution, the magnitude of each DFT component indicates, loosely speaking, how representative of the given pitch-class distribution the corresponding prototype is (Amiot 2016; Yust 2019). In other words, the DFT components behave as detectors of the corresponding prototypes.

The DFT was first proposed as a music-theoretical construct by Lewin (1959), and has recently been the object of renewed interest (Amiot 2016; Quinn 2007; Harding 2021). The representation introduced through DFT is agnostic with respect to notions such as key and tonality: as a consequence, it has been proposed as a viable analytical approach towards styles that exceed common-practice tonality, such as extended- and post-tonal repertoires in the 19th (Yust 2015b) and 20th (Yust 2015a; Harding 2020) centuries. As a computational tool, the DFT also lends itself to distant-listening approaches to large corpora.

Concurrently with musicological literature (e.g., Schönberg 1975; Kramer 1981; Brown 1986) and with results obtained with other quantitative methods (Moss et al. 2019, 2022), Yust (2019) showed corpus-based evidence supporting a decrease in diatonicity over a 350-years span of Western music, in particular during the 18th century, and an increasing diversification of harmonic idioms towards the end of the 19th century. Here, we attempt to track a similar unfolding in Debussy’s own creative development, which spans across the turn of the 20th century. In a DFT-based analysis of Debussy’s “Les sons et les parfums tournent dans l’air du soir”, Yust (2017) showed how individual DFT components correlate in an interpretable way with analytical insights, differentiating between diatonic-, octatonic-, and whole-tone-based structures in the piece. A greater salience of symmetric structures over asymmetric diatonic materials would be reflected by a DFT analysis in terms of a lower magnitude of the 5th component relative to the magnitudes of at least one of the other components. Similarly, the prevalence of different components (i.e., of different scale structures) in different regions of a piece may be computed to quantify the degree of fragmentation of the piece as a whole. These measures are formalised in Section “Methodology”.

Since different types of pitch-class structures may manifest themselves at different time scales inside a piece, it is necessary for our purposes to adopt a hierarchical perspective to the analysis of individual pieces. To this end, wavescapes (Viaccoz et al. 2022) have been recently proposed as an analytical and visualisation tool representing DFT analyses for every possible segmentation of a piece. Each piece is represented as a collection of six hierarchical graphs, where each node is a symbolic representation of a given segment of the piece. Each one of the six graphs is associated with one DFT component, and each node in the graph stores information about the magnitude and phase of the corresponding DFT component in the time span represented by the node. We propose in Section “Summary Wavescape” an extension of this approach by summarising the information of the six wavescapes into a summary wavescape, which stores information about the most salient DFT component for each time scale.

Aims and hypotheses

In summary, music-analytical accounts concurrently acknowledge Debussy’s departure from common-practice tonality. In particular, we focus on two aspects of this departure: tonal ambiguity and degree of fragmentation as defined in Sections “Symmetry and tonal ambiguity”, “Fragmentation as the coexistence of multiple pitch-class structures”. We aim at providing quantitative support for the claim that these features are indeed characteristic of Debussy’s compositional style, and that they are developed progressively throughout the composer’s life span. We also aim at testing whether such diachronic trends are associated with a decreased coherence, as captured by the notion of global prototypicality as introduced in Section “Global prototypicality as a form of coherence”. To this end, we conduct a corpus study over a novel dataset of Debussy’s entire œuvre for solo piano. Specifically, through a new representation derived from DFT analysis and wavescapes, we test whether

  1. 1)

    symmetric pitch-class materials are increasingly salient throughout Debussy’s life span, whereas asymmetric diatonic scales are decreasingly salient; and

  2. 2)

    the degree of fragmentation for individual pieces increases over Debussy’s life span, yet…

  3. 3)

    … the degree of coherence, as quantified by global prototypicality, does not decrease over Debussy’s lifespan.

Corpus

For this study, a novel corpus of digital scores representing Debussy’s entire œuvre for piano solo (1880–1917) has been assembled in a machine-readable XML format. To that aim, we used the original version of the Lesure work catalogue (Lesure 1977), discarding transcriptions and arrangements. The pieces for which digital scores were available online were manually checked against a print edition, whereas the missing ones were typeset by professional transcribers. This resulted in a dataset comprising 82 scores, each pertaining to an individual piece or movement, which can be viewed and modified with the free and open-source score editing software MuseScore. Metadata on the compositions, such as composition dates and identifiers, have been manually compiled from various web resources. The Python library ms3 was used to extract from the MuseScore files feature matrices with one row per note from which we computed the pitch-class vectors used in this study (Section “Wavescapes”). Data and code for reproducing the results are available on https://doi.org/10.5281/zenodo.7963255.

Methodology

As discussed in the introduction, in order to characterise Debussy’s departure from common-practice tonality, we exploited information contained in hierarchical DFT analyses through wavescapes (Viaccoz et al. 2022). We introduce a novel method to aggregate the information of the 6 wavescapes into a summary wavescape for each piece, and construct some ad hoc metrics on the summary wavescapes to assess our hypotheses quantitatively.

Wavescapes

In a piece, each connected segment spanning from onset position o for a duration of l quarter notes is represented as a 12-dimensional pitch-class vector (PCV) \(x(o,l)\): the p-th component \(x[p](o,l)\) represents the total duration of all notes with pitch class \(p \in [0,11]\) among the notes appearing between positions o and o + l in the piece. A piece is then represented as a hierarchy graph as shown in Fig. 2. Each node \(n_{o,l}\) in a hierarchy graph maps to a segment \(\pi (n_{o,l}) = x(o,l)\) of the piece. The graph’s edges are determined by defining node \(n_{o,l}\) as the parent of children nodes \(n_{o,l - 1}\) and \(n_{o + 1,l - 1}\). The leaves of the graph, corresponding to the shortest segments, are nodes \(n_{o,1}\) for \(1 \le o \le L\), where L is the total length of the piece in quarter notes; the root of the graph, corresponding to the entire piece, is \(n_{1,L}\). Note that, for an arbitrary node \(n_{o,l}\), the parameter l quantifies the geodesic distance from the leaves and is taken as a measure of the hierarchical height of the node: hierarchically higher nodes represent the pitch-class content of longer segments in the piece.

Fig. 2: Construction of the hierarchy graph for the opening passage of Ondine (L. 131, no. 8), spanning L = 6 quarter notes.
figure 2

The entire span of the passage is mapped to the root node of the graph on the right. The root’s children nodes correspond to two segments of duration L − 1, as indicated by the brackets below the score.

Full size image

The Discrete Fourier Transform (DFT) of a PCV is defined as

$$F:\Re _ + ^{12} \to C^{12},x \Rightarrow X(x)$$

with

$$X(x)[k] = \mathop {\sum}\limits_{p = 0}^{11} {x[p]e^{ - i2\pi p\frac{k}{{12}}}} .$$

Wavescapes after Viaccoz et al. (2022) can then be obtained by mapping each node n of a hierarchical graph to the tuple \(X(n): = X(\pi (n))\). A different wavescape \(X(n)[k]\) is then obtained for each distinct DFT component k. Each Fourier coefficient is a complex number with magnitude \(\left| {X(x)[k]} \right|\) – representing the intensity of the resonance between the node’s PCV and the corresponding Fourier component – and phase \(\phi (x)[k]\)– representing the transposition of the pitch-class set. The 0th coefficient represents the sum of the components of x, and the coefficients indexed from 11 to 6 are conjugates of those indexed from 1 to 6, respectively. As a consequence, only the coefficients \(k \in [1,6]\) are used in the wavescapes.

We normalised the magnitudes of the 6 coefficients in two steps. First, we normalised the magnitude of the 1st to 6th coefficients by that of the 0th coefficient. This constrains the magnitude values between 0 and 1. In addition, we apply a phase-dependent transformation of the magnitudes that, for each phase, scales the magnitude values so that the maximum magnitude for that phase is 1:

$$f_k(\phi ) = R\cos \left[ {\frac{\pi }{{N_k}}} \right]/\cos \left[ {\left( {\frac{\pi }{{N_k}}} \right) - \left| {\phi (x)[k]mod\frac{{2\pi }}{{N_k}}} \right|} \right]$$

where R is the radius of the polar plot, and N is the number of prototypes for a given coefficient k (\(N_n = {\textstyle{{12} \over n}}\) for n = 2, 3, 4, 6; \(N_n\) = 12 for n = 1, 5). The resulting transformation

$$\left| {\hat X(x)[k]} \right| = \frac{{X(x)[k]}}{{X(x)[0] \cdot f_k(\phi )}},k \in [1,6].$$

ensures that maximal magnitude values, associated with music-theoretically meaningful prototypes, are comparable across coefficients. For example, octatonic scales maximise the magnitude of the 4th coefficient for their value of phase just as (augmented) hexatonic scales maximise the magnitude of the 3rd coefficient for their value of phase: after the transformation, both are assigned unit magnitude.

The hierarchical graphs are visualised in six triangular coloured plots corresponding to the six distinct DFT coefficients, as shown in Fig. 3 (top). The intensity of the colour reflects the normalised magnitude of the coefficients.Footnote 2

Fig. 3: (Top) Black-and-white wavescapes for each DFT component in Ondine: in each wavescape, the opacity of each node is proportional to the magnitude of a DFT component.
figure 3

(Bottom) Summary wavescape with magnitude weighting: each node in the summary wavescape is coloured after the most resonant DFT component in the corresponding timespan of the piece.

Full size image

Summary Wavescape

As we are interested in identifying the most prominent DFT component in each segment of a piece, we combine the information from the six wavescapes into a summary wavescape by labelling each node in the hierarchy graph with its most resonant DFT component, as well as with a weight. Formally, summary wavescapes are obtained by mapping each node \(n_{o,l}\) of the hierarchy graph into the pair \(S_w\left( {n_{o,l}} \right) = (c_{o,l},w_{o,l})\), where

$$c_{o,l} = argmax_k|\hat X(o,l)[k]|$$

is the index of the most resonant DFT component for segment \(x(o,l)\), and \(w_{o,l}\) is a weight associated to the node. Note that, for notational convenience, we have defined \(X(o,l): = X(\pi (n_{o,l}))\).

In the following, we use two different weightings for the summary wavescape. In Section “Global prototypicality” we adopt

$$w_{o,l} = M_{o,l}: = |\hat X_{c_{o,l}}(o,l)|$$

as the magnitude of the most resonant DFT component (magnitude weighting). In Section “Symmetric vs asymmetric structures” we use instead

$$w_{o,l} = H_{o,l}: = 1 - \mathop {\sum}\limits_{k = 1}^6 {\frac{{|\hat X(o,l)[k]|log|\hat X(o,l)[k]|}}{{log6}}}$$

based on the (normalised) entropy of the 6 components’ magnitudes (entropy weighting). This value is inversely related to the uncertainty about the component labelling the node: if several different components have similarly high magnitudes, the uncertainty about which is the highest increases while the weight \(H_{o,l}\) decreases.

The summary wavescape is visualised as a triangular coloured plot where the colour of each node is determined by the index \(c_{o,l}\) of the most resonant coefficient and the intensity is proportional to the weight \(w_{o,l}\). The summary wavescape for Ondine from the second book of Préludes (L. 131, no. 8) can be seen at the bottom of Fig. 3.

To exemplify the interpretation of a summary wavescape, we examine Debussy’s Ondine, introduced in Section “Fragmentation as the coexistence of multiple pitch-class structures”. The music of mm.37–44ff. transitions every two measures into a different type of pitch material, each corresponding to a distinct, most resonant DFT coefficient, as illustrated in Fig. 4.

Fig. 4: Prominent DFT coefficients in different segments of Ondine, mm 37–44ff (bottom) and the summary wavescape for the entire passage (top).
figure 4

Each coefficient reflects the character of the corresponding bars: whole-toneness (6th, purple), diatonicity (5th, blue), augmentedness (3rd, green), chromaticity (1st, red), and octatonicity (4th, cyan) as discussed in Section “Fragmentation as the coexistence of multiple pitch-class structures” (cf. Fig. 1). Note how the entire section may be best subsumed under an overall octatonic pitch-class distribution, as shown by the cyan colouring of the hierarchically highest nodes in the graph.

Full size image

Examining the overall structure of the work, the summary wavescape immediately suggests a more fragmented arrangement of the first half of the piece in comparison to the second half, as identified, e.g., in the analysis by Wheeldon (2004). Despite the considerable amount of fragmentation, the summary wavescape reveals a significant degree of hierarchical coherence in the piece: the nodes in the topmost levels (corresponding to larger segments) exhibit a vivid prevalence of the 4th coefficient, indicating that the pitch material is generally organised octatonically at large timescales. Conversely, a low degree of hierarchical coherence would be found if hierarchically higher-level nodes had low opacity (magnitude) compared to lower-level nodes. This would indicate that larger segments of the piece cannot be ascribed to a defined prototypical pitch-class structure since they are characterised by a more uniform, possibly musically uninterpretable distribution of pitch classes.

Symmetric vs asymmetric structures

To quantify the adoption of different types of pitch materials, and assess hypothesis 1 that the use of diatonic materials decreases over time whereas the use of symmetric materials increases over time, we propose a metric that measures the prevalence of every coefficient in each piece. Specifically, we define the “prevalence” \(W(k)\) of coefficient k in a piece as the proportion of the summary wavescape’s nodes where coefficient k has the highest normalised magnitude, weighted by the summary wavescape’s entropy weighting. Formally, \(W(k) = {\textstyle{1 \over N}}\mathop {\sum}\nolimits_{o,l} {H_{o,l} \cdot \delta _{c_{o,l},k}}\), where N is the total number of nodes in the summary wavescape, and δ stands for Kronecker’s delta function, which here acts as the indicator function of the set of the nodes in the summary wavescapes that are attributed to coefficient k.

Fragmentation

In order to address hypothesis 2 that the degree of fragmentation increases over time in Debussy’s piano works, we need to characterise the degree of fragmentation of a piece. Loosely speaking, we interpret the variability in the labelling in the hierarchy graph as an indicator of the degree of fragmentation of the corresponding piece, so that a piece that is entirely characterised by a single label across the hierarchy graph is minimally fragmented, and vice versa. Note that the set of the regions of neighbouring nodes with identical labels (i.e., visualised as having identical colour) forms a partition of the hierarchy graph. More precisely, we define the probability space \((X,P(X),\mu )\), where X is the set of nodes of the pieces’ hierarchy graph, \(P(X)\) is the power set of X, and \(\mu :P(X) \to [0,1]\) is a probability measure that quantifies the size of any subset \(Y \subseteq X\) as \(\mu (Y) = |Y|/|X|\). Considering that the summary wavescape labels nodes of the hierarchy graph with a coefficient index \(c_{i,j}\), we define the maximal connected region \(A_{n_{o,l}}\) around node \(n_{o,l}\) as the largest set comprising nodes \(n_{o\prime ,l\prime }\) that are neighbours to each other and such that \(c_{o\prime ,l\prime } = c_{o,l}\). Two nodes are considered to be neighbours if they are connected by an edge in the hierarchy graph. The set \(A = \{ A_n\} _{n \in X}\) is then a partition of X, and we then quantify the degree of fragmentation as the measure-theoretic entropy \(H(A) = - \mathop {\sum}\nolimits_{A_n \in A} {{\textstyle{{\mu (A_n)\log \mu (A_n)} \over {\log |X|}}}}\) of the partition A. The measure-theoretic entropy quantifies the uncertainty about what coefficient governs a randomly-selected segment of the piece. The measure, therefore, takes into account the distribution and clustering of the most resonant DFT components across the hierarchical structure of the piece.

Global prototypicality

Hypothesis 3 states that global prototypicality, as a proxy of coherence, does not decrease over time. Global prototypicality refers here to the degree to which the pitch-class content of larger segments of a piece expresses some pitch-class prototype, as opposed to a uniform distribution over pitch-classes. Such a feature would be reflected in the DFT components by increasing magnitudes for at least some DFT coefficients, with the magnitudes for a perfectly uniform distribution being zero for all coefficients. In particular, we are interested to quantify how this feature degrades as shorter segments are combined to form longer and longer segment. Formally, the magnitude weighting \(M_{o,l}\) of the summary wavescape reflects the highest resonance amidst the 6 coefficients. In a nutshell, it shows how strong the resonance of any structure in the given node is. To quantify global prototypicality we calculated the average maximal magnitude for each hierarchical level l as \(V_l = {\textstyle{{\mathop {\sum}\nolimits_o {M_{o,l}} } \over {n \,-\, l}}}\), where n − l is the number of nodes at each hierarchical level. We then computed the degree of incoherence as the slope P of the regression line \(V_l = P \cdot (l/L) + c\), where c is an intercept term.

Results

In order to investigate the presence of linear trends over time for each of the quantitative features defined above, data were analysed with Bayesian mixed-effects models provided with weakly informative priors (a Student’s t-distribution with parameters (3,0,1); cf. Gelman et al. 2008) and implemented in the R package brms (Bürkner 2018). Each model characterises the observed values of the dependent variable as samples from Gaussian distributions whose means are modelled as a function of the predictor variables indicated to the right of the symbol ~ (Gelman et al. 2013; Bürkner 2018). In the following, given two variables A and B, the notation A × B indicates a linear combination of the main effects of A and B, as well as their interaction A:B. We report the effect size (β) as well as the evidence ratios (\(Odds(\beta \gtrless 0)\)) for an effect to be larger or smaller than zero. From a frequentist perspective, evidence ratios can be interpreted as significant (*) at a .05 confidence level when exceeding 19 (Milne and Herff 2020). Data and code for reproducing the analyses are available at https://osf.io/ncw84/.

Hypothesis 1

Figure 5a shows the diachronic trends for each coefficient’s entropy-weighted prevalence, by means of locally-estimated scatterplot smoothing (LOESS) curves fitted over 100 randomly sampled subsets of the data. Trendlines highlight a marked decrease in the prevalence of diatonicity (5th coefficient) across the composer’s production for piano. Relatively larger prevalence for components that correspond to symmetric prototypes, in particular the 2nd, 3rd, 4th, and 6th can be observed in pieces composed after the turn of the 20th century compared to earlier years.

Fig. 5: Change over time of the entropy-weighted prevalence for each of the six DFT coefficients.
figure 5

a Each panel shows the entropy-weighted Prevalence W of the corresponding DFT component across all pieces in the corpus (dots), as a function of the composition year. For each component, one-hundred bootstrapped LOESS curves are shown to highlight the diachronic trends in the data. b Posterior distributions of the effect of the composition year on the entropy-weighted prevalence for each of the six DFT components. Strong evidence was found for the decreasing and increasing trends observed for the fifth and the fourth coefficients, respectively.

Full size image

In order to quantify evidence for the presence of an overall trend in the data, the entropy-weighted prevalence \(W(k;x)\) of coefficient k in the summary wavescape for piece x was modelled as

$$W(k;x)\sim k \times y(x) \times L(x) + (1 + L(x)|x),$$
(1)

where k is represented as a categorical variable spanning values 1 to 6 to model the different DFT components (the 5th component being arbitrarily chosen as the reference level), y(x) is the composition year and L(x) is the length measured in quarter-note units of piece x.Footnote 3 The model includes the main effects as well as the interaction terms of year and piece length, and also allows for a random intercept over pieces \(\left( {1{{{\mathrm{|}}}}x} \right)\) and a random-slope term \((L(x)|x)\) (cf. Bürkner 2018). The latter account for the fact that the effect of the length of a piece on the coefficient magnitudes may be different across pieces. For example, compared to short pieces, longer pieces may tend to exhibit a larger variability in pitch-class content over their entire duration, resulting in lower and more uniform magnitudes across all coefficients in higher hierarchical positions (corresponding to large proportions of the piece). As a consequence, summary wavescapes of longer pieces may tend to exhibit lower prevalence values on average, and this would be accounted for by the fixed effect of piece length. However, this effect may be different for fast-paced or texturally denser pieces compared to slow or texturally sparse pieces, and this variability across pieces is captured by the random-slope term.

As shown in Fig. 5b, strong evidence was found for a negative effect of composition date on the prevalence of the 5th coefficient (\(\beta (y) = - 0.68,SE = 0.09,Odds(\beta (y) \,<\, 0) \,>\, 9999^ \ast\)), supporting that diatonicity in the corpus decreases over time. The prevalence for all other coefficients, \(k \,\ne\, 5th\), exhibit a significantly less negative effect of composition date (all \(Odds(\beta (k:y) \,>\, 0) \,>\, 9999^ \ast\)). In particular, a significant linear increase over time was observed for the prevalence of the 4th coefficient (\(\beta (y + 4:y) = 0.20,SE = 0.10,Odds(\beta (y + 4:y) \,>\, 0) = 52.81^ \ast\)), while no such evidence was found for the other coefficients (all \(Odds(\beta (y + k:y) \,>\, 0) \,<\, 2\)). Longer pieces also exhibited lower prevalence of the 5th coefficient compared to shorter pieces (\(\beta (L) = - 0.39,SE = 0.11,Odds(\beta (L) \,<\, 0) > 9999^ \ast\)), while little to no evidence was found that the prevalence of the other coefficients varied with the length of the piece (all \(Odds(\beta (L + k:L) \,<\, 0) \,<\, 10\)).

Overall, these results support Hypothesis 1 by showing that diatonicity was progressively less salient from Debussy’s youth to his maturity, while pitch-class materials based on the other symmetric prototypes remained stable or, in the case of the 4th coefficient, increased over time. Similarly, longer compositions exhibited a lower degree of diatonicity.

It should be noted, though, that prevalence in the summary wavescape is heavily influenced by the piece’s surface, which accounts for a large portion of the wavescape’s nodes. In other words, it is possible that the observed decrease in diatonicity was due to surface phenomena, such as an increase in ornamental chromaticism, rather than to a departure from diatonicity as an overarching structural principle governing a piece across hierarchical levels. In order to investigate this alternative explanation, we conducted a post-hoc analysis where prevalence was replaced with a different measure that weighs surface nodes less than those that lie higher in the hierarchy.

Post-hoc analysis of hierarchical prevalence

We define the moment of inertia MoI of coefficient k in the summary wavescape as \(I(k) = {\textstyle{1 \over N}}\mathop {\sum}\nolimits_{o,l} {w_{o,l} \cdot (l/L)^2 \cdot \delta _{c_{o,l},k}}\), where l is the length of the segment in the summary wavescape (and therefore its height in the hierarchy) and L is the total length (in quarter-note units) of the piece. The moment of inertia gives more weight to nodes appearing on high levels of the hierarchy, and is, therefore, less influenced by noise in the lower hierarchical levels. Intuitively, this measure is the moment of inertia of the region of the wavescape associated with component k when rotated around an axis that passes through the hierarchy graph’s leaves.

The diachronic development of moment of inertia was modelled as in Eq. (1), where \(W(k;x)\) was replaced with \(I(k;x)\). As shown in Fig. 6, the negative effect of composition date on the 5th coefficient for the MoI was also supported by strong evidence (\(\beta (y) < 0 = - 0.59,SE = 0.10,Odds(\beta (y) < 0) > 9999^ \ast\)). Analogously to the findings for the coefficients’ prevalence, the effect of composition date on all other coefficients was significantly less negative (all \(Odds(\beta (k:y) > 0) > 9999^ \ast\)), and the MoI of the 4th coefficient was found to increase significantly over time (\(\beta (y + 4:y) = 0.21,SE = 0.10,Odds(\beta (y + 4:y) > 0) = 54.05^ \ast\)). Overall, these findings support that the observed decrease in diatonicity in favour of the octatonic-based pitch-class materials is not the result of surface phenomena, and rather reflects a tendency for segments across all hierarchical levels to be less and less governed by diatonic structures in later pieces.

Fig. 6: Posterior distributions of the effect of the composition year on the moment of inertia of each of the six DFT components.
figure 6

Significant decreasing and increasing trends were found for the fifth and the fourth coefficients, respectively.

Full size image

Hypothesis 2

Figure 7 shows the diachronic trend of fragmentation over time. We investigated the presence of an overall trend across Debussy’s pieces by training model

$$H(x)\sim y(x) \times L(x),$$

which predicts the degree of fragmentation for piece x as a function of the composition date \(y\), the length of the piece L, as well as their interaction. Strong evidence was found that fragmentation increases over time (\(Odds(\beta (y) = 0.42,SE = 0.11,\beta (y) > 0) > 2399^ \ast\)). No evidence was found for an effect of the pieces’ length (\(\beta (L) = - 0.05,SE = 0.13,Odds(\beta (L) > 0) = 0.54\)), nor that the diachronic trend is modulated by the pieces’ lengths (\(\beta (y:L) = - 0.09,SE = 0.12,Odds(\beta (y:L) > 0) = 0.21\)). Overall, these results support a development in Debussy’s style in the direction of increasing fragmentation.

Fig. 7: Fragmentation of each piece (dots) and corresponding trend lines over time, represented as 100 LOESS curves under bootstrapping.
figure 7

A significant increasing trend was found.

Full size image

Hypothesis 3

Similarly, we investigated the degree of global prototypicality across Debussy’s pieces. The corresponding trend over time is shown in Fig. 8. With model

$$P(x)\sim y(x) \times L(x)$$

we found evidence for an increase over time (\(\beta (y) = 0.26,SE = 0.12,Odds\left( {\beta (y) > 0} \right) = 68.23^ \ast\)) and over pieces’ lengths (\(\beta (L) = 0.37,SE = 0.14,Odds(\beta (L) > 0) = 273.81^ \ast\)), with no significant interaction effect (\(\beta (y:L) = 0.08,SE = 0.12,Odds(\beta (y:L) > 0) = 2.83\)). Furthermore, Global Prototypicality and Fragmentation were positively correlated to one another (\(r\left( {80} \right) = 0.56,p \,<\, 0.001\)). These results are compatible with the hypothesis that the increase of fragmentation is not associated with an overall decrease in coherence in Debussy’s style as quantified by P.

Fig. 8: Global prototypicality of each piece (dots) and corresponding trend lines over time, represented as 100 LOESS curves under bootstrapping.
figure 8

No evidence for an overall decreasing trend was found.

Full size image

Discussion

In this paper we conducted a diachronic study on Debussy’s piano solo music to investigate the evolution of the composer’s personal style. We focused on Debussy’s progressive departure from common practice tonality under three music-theoretically motivated assumptions (Parks 1980; Tobin 2002; Wheeldon 2004). We expected a decreasing use of diatonic pitch structures in favour of symmetric pitch structures such as octatonic and whole-tone scales. Furthermore, we hypothesised an increase over time in fragmentation, with the use of multiple scales and pitch-class structures inside the same composition. Finally, this increase in fragmentation, we hypothesised, would not yield a decrease over time in the overall coherence of pieces, as reflected by their global prototypicality. We adopted a distant listening approach to evaluate the three hypotheses, and we quantified relevant estimates of prevalence, fragmentation, and global prototypicality using ad-hoc metrics based on the DFT. Our results were largely consistent with these hypotheses and quantitatively revealed a change in Debussy’s practice in terms of tonal ambiguity and fragmentation, proving the relevance of these two features in the development of the composer’s style.

First, the observed decrease in the prevalence of the 5th coefficient from early to late pieces indicates a progressive loss of salience of diatonic structures over time. This is also consistent with a shift towards the prevalent adoption of symmetric pitch-structure prototypes, as opposed to the asymmetry of diatonic ones, although asymmetric pitch-structures may also emerge from the combination of symmetric prototypes. Overall, this result supports a development of Debussy’s music in the direction of renouncing the features of directedness and orientation in pitch-space that characterise diatonicity. As discussed in Section “Fragmentation as the coexistence of multiple pitch-class structures”, we interpret this as empirical evidence of a shift towards introducing blurriness and ambiguity in the tonal idiom.

It is worth noting that the appearance of the 5th coefficient is, in principle, not solely associated with heptatonic major/minor scales, but more generally to both heptatonic and pentatonic modes (Viaccoz et al. 2022). Modal and, most notably, pentatonic scales are often identified as characteristic of Debussy’s writing (Tymoczko 2004; Uchida 1990), contribute to a sense of tonal ambiguity by weakening functionality and directedness (Green 1992; Pomeroy 2003), and may also be expected to become increasingly salient as alternatives to common-practice diatonicity. As both diatonic and pentatonic scales resonate with the 5th DFT component, the observed decline in that component suggests that the use of modal and pentatonic scales is either not subject to an increase over time, or that such increase is small enough that it cannot compensate for the opposite trend of (heptatonic) diatonicity. An overall diachronic decrease in the use of pentatonic scales, mirroring the decline of diatonic scales, would also be consistent with the observed results, but this seems at odds with analytical insights from the close-reading of the repertoires (Alegant 2016; Day-O’Connell 2009; Kopp 1997). Future research may further address the differentiation between prototypes associated with the same coefficient (i.e., diatonic and pentatonic, octatonic and diminished sevenths).

Components corresponding to non-diatonic prototypes achieved, to different degrees, larger prevalence in later pieces (cf. Fig. 6A), especially in the timeframe that comprises compositions like Estampes (1903), Images (1907), and Préludes (1909–1912)—highly representative of Debussy’s own “impressionist” style (Roberts 2001). In particular, we found strong evidence that the observed decrease in diatonicity was compensated by an overall increase in the prevalence of the 4th DFT component from early to late pieces. This finding is consistent with the reported importance of octatonic sonorities in Debussy’s harmonic style (Forte 1991; Polth 2011). Besides the use of octatonic structures for the sake of their peculiar sounding quality, the prominence of the 4th coefficient may also reflect one of the possible interpretations of octatonic structures as hypothesised in the context of extended tonality by the Tonfeld theory (Haas 2004; Polth, 2006; Schiltknecht, 2011), its precursors (Lendvai, 1971), as well as related scholarship (Giannetta 2007; Grande 2013; Smith 2020). In such theories, the notion of tonic, subdominant, and dominant function that is constitutive of common-practice tonality can be generalised into the relationship among three sets of pitch classes, each corresponding to an octatonic collection. From this perspective, the prominence of octatonicity (compensating the opposite trend of diatonicity) may then reflect the preservation of some generalised notion of harmonic functionality while abandoning the characteristic sonorities of diatonic tonality in favour of chromatic ones. Further investigation of this hypothesis through close-reading analyses as well as quantitative methods could offer additional grounding to attempts to frame the complex and elusive features of extended tonality into a coherent theory (cf. Rohrmeier and Moss 2021) and support the interpretation of octatonic structures as expressing extended-tonal harmonic functionality (Cecchetti et al. 2022).

These results were further strengthened by an analysis where the prevalence of a DFT component in the summary wavescape was attributed a higher weight in longer segments than in shorter ones. Specifically, this was quantified as the moment of inertia of the region of the summary wavescape where the given DFT component had the largest magnitude. The components’ moments of inertia were found to exhibit an analogous behaviour as their unweighted prevalence. These results indicate that the observed diachronic growth of octatonicity was not primarily driven by a stylistic evolution concerning the piece’s surface (i.e., by the many short segments comprising the lower portion of the summary wavescape), but rather reflected an increasing tendency to employ octatonic structures at all hierarchical levels.

By comparison, the corpus study by Yust (2019) also identified a decreasing trend for diatonicity in the later part of a timeframe spanning from the sixteenth to the nineteenth century, alongside increasing trends for other components. Although works by Debussy were not included in Yust’s corpus, and Debussy’s birthdate is posterior to that of all the composers who were included in the corpus, Yust’s results for the late nineteenth-century characterise a stylistic landscape that Debussy would eventually become a part of, and that may have had an influence on him. The results in the present study partially overlap with the ones observed in the historically broader corpus, although overall increasing trends over the composer’s lifespan were only supported by strong evidence for the prevalence of the 4th coefficient. This may reflect a peculiarity of Debussy’s mature style relative to his contemporaries: indeed, the special role of octatonic constructions—the prototypical structures that resonate with the 4th DFT component – has been frequently highlighted as a characteristic feature in Debussy (Giannetta 2007; Parks 1980; Tobin 2002). It is also possible that Debussy did inherit some aspects of the compositional style from his close contemporaries, but that this compositional style was, by then, already mature in the form that is captured by Yust’s results: if this was the case, the trends that characterised the nineteenth century would not be further developed during Debussy’s lifetime.

Beyond the departure from diatonicity, we observed a significant increase of the pieces’ fragmentation over time, indicating that later pieces tend more and more to resonate with different DFT components in different segments across hierarchical levels. Note that this is a global property of a piece and does not necessarily reflect a more fragmented musical surface, which would be reflected as a larger number of contiguous regions with different colour in the lower nodes of the summary wavescape. While features of the musical surface, such as bar-by-bar switches across different scale types, are likely to be more salient to the listeners’ perception, we were interested here in investigating the compositional style rather than the listeners’ experience. Accordingly, fragmentation as quantified in our analysis was meant to reflect an overarching compositional plan of the piece across all timescales, whereas future studies may rather focus on the listener’s perceptual impression.

Finally, we also found evidence that the global pitch-class set prototypicality of Debussy’s pieces, loosely defined as the capacity of larger segments of a piece to still express a definite pitch-structure prototype, rather than an undefined uniform distribution of pitches, was non-decreasing over time. We interpret this finding as supporting the musicological insight that Debussy’s stylistic evolution did not result in mere “distortions, contradictions and exoticisms” pouring confusion into the tonal harmonic idiom (Parks 1980), but rather contributed to a coherent and highly organised personal idiom (Tobin 2002). Clearly, global prototypicality is a neither necessary nor sufficient characterisation of the internal coherence of pieces, as a musical idiom may rely on completely different principles. Nevertheless, global prototypicality does capture a generalisation of an aspect of stylistic coherence that is characteristic of common-practice tonality: namely, the notion that a piece as a whole is as much an expression of its global diatonic key as its smaller segments are expression of their local one. This characteristic of tonal pieces is reflected by their resonance with individual diatonic sets both at low and high hierarchical levels (Lieck and Rohrmeier 2020; Viaccoz et al. 2022). The observed trend in global prototypicality for Debussy’s pieces is consistent with the hypothesis that the composer’s idiom retained to some extent this hierarchical notion of coherence in his compositions, while generalising it beyond the diatonic set alone.

From a methodological perspective, it should be noted that the DFT coefficients of two PCVs having phases which are radially opposite cancel out the corresponding magnitudes when the two PCVs are merged together. For instance, computing the DFT on a segment of music containing both prototypical whole-tone scales in equal proportions would exhibit a null magnitude in the corresponding coefficient, the 6th, and, therefore, would not be picked up in our analysis. Musicological literature has highlighted a frequent use, in Debussy’s production, of alternating or juxtaposing whole tone scales (Uchida 1990). Regions characterised by such alternating structure would then fail to resonate strongly with the 6th coefficient, and the absence of an increase in the prevalence of the 6th coefficient over time is also consistent with an increasing use of whole-tone scales according to this juxtaposition practice. On similar grounds, the absence of an increase in the prevalence of the 3rd coefficient is also consistent with an alternating use of structures based on different augmented triads. Music-theoretical accounts of extended tonality such as Neo-Riemannian (Cohn 2012) and Tonfeld theory (Haas 2004) associate the compositional role of augmented triadicity with the expression of contrasts through the juxtaposition of different triadic poles (Rohrmeier and Moss 2021), and a prevalence of such harmonic practice would not be reflected by an increase in the prevalence of the 3rd coefficient in our analysis. In summary, it is possible that the absence of increasing trends for coefficients other than the 4th may be due to the corresponding pitch-class prototypes being systematically used in the context of contrasting patterns where they are instantiated with opposite phases. This calls for the development of quantitative methods to complement the present findings in future research.

More generally, this approach offers a heuristic for detecting structural features of music that, by construction, does not take into account the temporal order of individual events and, as a consequence, the phenomenology associated with voice-leading and melodic motion. Nevertheless, the role of temporal adjacency was to some extent accounted for by modelling a musical piece as the hierarchical nesting of recursively smaller building blocks, the hierarchy graph.

A further methodological consideration for this as well as future analogous studies has to do with the normalisation of relevant quantities. First, normalisation is crucial for comparing among the magnitudes of different DFT components (Amiot 2016). Here, we introduced a phase-dependent transformation that equalised the maximum magnitude for each phase across coefficients. This was meant to highlight the pitch-structure prototypes of each coefficient, making their resonance comparable in magnitude. Normalisation was also crucial for comparing across different pieces. In our analyses, we computed hierarchical height as a fraction of the pieces’ length, thus effectively normalising pieces to unit duration. This, together with the inclusion of the effect of length in our models, served the purpose of avoiding confounding effects for long or short pieces. Nevertheless, many features of the pieces, possibly confounded with length, may also have an impact on our measures. For instance, the tempo, the event density, as well as other textural features may influence the relative pace with which new events are introduced, hence potentially impacting the identifiability of pitch-class-structure prototypes at higher hierarchical levels. Future research may further explore this possible interaction of textural and structural features, and its implications for hierarchical analyses based on the DFT.

Conclusion

The music by Debussy presents significant challenges to analytical investigation, in that it departs from common-practice diatonic tonality while instantiating a novel harmonic idiom. In this study, we employed a computational corpus-based approach to investigate the diachronic development resulting in the emergence of Debussy’s personal style. By analysing the composer’s entire solo-piano works with Discrete Fourier Transform we supported with strong empirical evidence the hypothesised decrease over time in diatonicity, which was found to be accompanied by an increase in octatonicity and fragmentation but no decrease in global coherence. The observed increase in the use of, in particular, octatonic materials may reflect a shift towards a generalised system instantiating functional harmony in a chromatic context, as hypothesised by theories of extended tonality such as Tonfeld theory (Haas 2004). These results complement and extend traditional music-analytical insights by identifying well-defined features that undergo a transformation during the composer’s lifetime, and providing corpus-based statistical evidence for specific qualitative hypotheses stemming from the close-reading of individual pieces. This contributes to characterise the historical emergence of extended-tonal compositional techniques in the late 19-th century by example of Debussy’s work. Ultimately, the three ad-hoc metrics designed for this study may find interesting applications to the empirical investigation of other musical repertoires where the use of symmetric pitch-class patterns is problematised by qualitative research, including extended-tonal and post-tonal repertoires from the late Nineteenth century until our days.