Liability-driven investment for pension funds: stochastic optimization with real assets

Abstract

Using a multi-stage stochastic programming method, we suggest an optimal liability-driven investment (LDI) strategy for a closed defined-benefit pension fund including real assets. The objective is to jointly optimize contribution, funding ratio, and buyout cost, subject to a constraint on downside risk in terms of expected shortfall of assets relative to liabilities. Over a 10-year planning horizon, the optimal LDI strategy with a key-rate duration-matching bond portfolio outperforms the corresponding strategy with a duration-convexity matching bond portfolio as well as a strategy with an aggregate bond index-tracking portfolio. When real assets are introduced, the optimal LDI strategy includes significant investment in infrastructure and real estate, illiquidity notwithstanding. Nevertheless, delays in sales of real assets induced by illiquidity can increase downside risk.

Introduction

As financial markets have come to terms with the impact of Covid-19 and gradual shutdown of large parts of the global economy, pension scheme managers have once again been reminded that they face a vast array of risks that can derail their investment strategies and, potentially, pose a serious threat to their commitments to scheme members. Since the Global Financial Crisis, more and more pension schemes have adopted a Liability Driven Investment (LDI) approach to managing the many risks that they face as they aim to fulfil their main goal, that is, to make all pension payments due to scheme members in full and on time.

LDI is a holistic investment strategy applied not only to the asset side of the pension scheme balance sheet, but also to the liability side. It recognises that the optimal investment strategy for an investor with liability differs from conventional asset-only strategies. Ang et al. (2013) and Sharpe and Tint (1990) incorporate liability and shortfall risks into a static mean-variance framework. Rudolf and Ziemba (2004) and Detemple and Rindisbacher (2008) solve a continuous-time dynamic portfolio problem with liability for a risk-averse pension manager, whose decisions are determined by maximizing the expected utility of funding ratios and contributions. They determine appropriate hedge instruments or dynamic strategies for optimally managing a pension fund, but there is little comparison or demonstration of implementable bond strategies, in a practical setting.

As the record low yields of Treasury bonds continue after the quantitative easing policy triggered by the Global Financial Crisis, pension fund managers are searching for alternative assets. To unload sponsors’ contribution burden, employing a simple liability-hedge strategy is not enough, and this is where growth assets come in. In particular, there is an increasing interest in real assets which can provide relatively stable and inflation-linked cash flows and which also benefit from lower correlation with traditional asset classes and pension liability (Hertrich 2013; Weber et al. 2016). Pension asset allocation to real assets, such as real estate, private equity, and infrastructure increased by 17–23% from 6% over the last 20 years (Hodgson et al. 2020). This investment, however, requires a long holding period to avoid potential losses caused by high joining and withdrawal fees; in other words, the illiquidity problem must be mitigated. The importance of real assets has grown, but there are no academic studies investigating the effect of real assets on the LDI framework.

In order to compare practical hedge portfolios and to investigate the effect of real assets, we apply a computational approach called multi-stage stochastic programming (MSP) to a multi-period investment problem for a closed defined-benefit pension fund. Over a certain planning horizon, the objectives are as follows: (1) to increase and stabilise funding ratios; (2) to lower and limit contributions; and (3) to minimize buyout cost at the end of the planning period. Arguably, these objectives comprehensively describe any LDI strategy. Given these objectives, we analyse the performance of three bond portfolios, namely an aggregate bond index-tracking portfolio, a duration-convexity matching portfolio, and a key-rate duration-matching portfolio, in the context of stochastic non-parallel shifting of Treasury and pension discount yield curves. Using a novel structure of linear liquidity penalty, we also examine the effect and role of four real asset classes: real estate, infrastructure, timber, and agriculture.¹

Our multi-stage stochastic programming model allows us to investigate the benefits of an LDI approach to pension scheme management. Stochastic programming is a mathematical framework for optimization problems with uncertainty in economic, financial, actuarial, and demographic variables (Barro et al. 2022; Consigli et al. 2017; Birge and Louveaux 2011; Ziemba 2003), with recent theoretical developments collected in Carpentier et al. (2015). Applications of stochastic programming in an LDI context can be found in Georgiopoulos (2020), Duarte et al. (2017), Aro and Pennanen (2017), Geyer and Ziemba (2008), Hilli et al. (2006), Kouwenberg (2001). They consistently show that investment strategies found by using stochastic programming are superior to any fixed-mix investment strategies. This is because these frameworks can deal with practical features such as complex market dynamics and pension scheme regulations, that are an important part of defined-benefit pension planning. Practical constraints such as those relating to transaction costs, regulatory restrictions, and taxes can subsequently be included. Stochastic programming is also useful in personal retirement planning and in lifecycle investment (Owadally et al. 2021a; Owadally et al. 2021; Kim et al. 2020; Simsek et al. 2018; Consiglio et al. 2015; Konicz et al. 2015; Konicz and Mulvey 2015, 2013).

The paper is organized as follows. In the next section, we describe the main objectives of a defined-benefit pension fund. Section 3 comprises a model of financial markets within a vector auto-regressive framework. Section 4 formulates an optimization problem under the MSP framework, and Sect. 5 presents numerical results and interpretations. We summarize our findings in the last section.

Objectives of a defined-benefit pension fund

Funding ratio, contribution, and buyout cost

One of the main objectives when managing the investment portfolio of a defined-benefit pension plan is to maintain full funded status. Let total asset and liability values at time t be denoted by $A_t$ and $L_t$, respectively, so that $A_t/L_t$ is the funding ratio. The funding ratio is regularly monitored by pension regulators to secure the current and future benefits of pension members. The function below shows the expected utility of the funding ratio at time t, within an investment planning horizon (0, T]. The utility function u is concave, under the assumption of risk-aversion.

$$\begin{aligned} \mathbbm {E}\left[ u\left( \frac{A_t}{L_t} \right) \right] \end{aligned}$$

In addition to benefit security, the pension fund manager should also consider contribution stability, in order to provide budgetary certainty for the plan sponsor’s operating business. Another objective for the pension manager is therefore to maintain a sustainable level of contribution. We apply a convex disutility function d to contribution $C_t$ at time t relative to a target contribution $\hat{C}$. The expected disutility of the relative cost is as follows:

$$\begin{aligned} \mathbb {E}\left[ d \left( \frac{C_t}{\hat{C}} \right) \right] . \end{aligned}$$

In this research, we are concerned only with a closed defined-benefit pension scheme, which means that there are no new entrants to scheme membership. Many sponsors of this type of pension scheme are willing to contemplate buyout of their liabilities by an insurer because this makes their balance sheet less volatile. The final objective that we consider is to maintain the buyout cost close to a target level $\hat{B}$, which may be interpreted as a premium paid to an insurer because the insurer assumes the pension liabilities in exchange for the pension assets and the buyout premium. This objective is expressed as the expected disutility of a ratio of the final contribution $C_T$ to the target buyout cost $\hat{B}$ at the terminal horizon T:

$$\begin{aligned} \mathbb {E}\left[ d\left( \frac{C_T}{\hat{B}}\right) \right] . \end{aligned}$$

The objectives of the pension scheme manager and sponsor are formulated by maximizing the following expression:

$$\begin{aligned} \sum _{t=1}^{T}{\lambda \ \delta ^t\mathbb {E}\left[ u\left( \frac{A_t}{L_t}\right) \right] }-\sum _{t=0}^{T-1}{\left( 1-\lambda \right) \delta ^t\mathbb {E}\left[ d\left( \frac{C_t}{\hat{C}}\right) \right] }-\left( 1-\lambda \right) \delta ^T\mathbb {E}\left[ d\left( \frac{C_T}{\hat{B}}\right) \right] . \end{aligned}$$

(1)

The time preference parameter $0<\delta \le 1$ controls the relative importance, to the scheme manager and sponsor, of earlier contributions and funding ratios over later contributions and funding ratios. The weighting factor $0<\lambda <1$ balances the funding ratio objective and the contribution objective, related to benefit security and contribution stability, respectively.

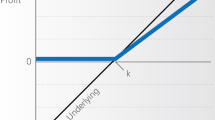
Figure 1 shows representative shapes of linearized utility and disutility functions. The concave utility function in panel 1a consists of three piecewise linear segments or zones. By changing their marginal values, we can impose more concavity, i.e. preference for higher risk-aversion. Convexity changes in a similar fashion for the disutility function in panel 1b. The approximation of non-linear concave and convex functions by means of piecewise linear functions is also used by Dempster and Medova (2011), Medova et al. (2008). This transforms the optimization problem to a stochastic linear program.

Fig. 1

Piecewise linear utility and disutility functions

Downside risk

Apart from the above-mentioned objectives, we constrain downside risk of the pension fund. We measure downside risk by means of the shortfall, which is the deficit in the pension fund or the excess of liability over assets. The expected shortfall at level $1-\alpha$ measures the downside risk at time t. The shortfall is equal to difference between total liability and asset values, so our model does not allow any dynamic investment decision that causes the expected shortfall at level $1-\alpha$ below an expected shortfall target, ${EST}_{t;1-\alpha }$. Following Rockafellar and Uryasev (2002), we add the following constraint to our optimization model.

$$\begin{aligned} {VaR}_{t;1-\alpha }+\frac{1}{(1-\alpha )} \mathbbm {E}\left[ {\left[ L_t-A_t- {VaR}_{t;1-\alpha } \right] }^+ \right] \le {EST}_{t;1-\alpha }, \end{aligned}$$

where $L_t-A_t$ and ${VaR}_{t;1-\alpha }$ represent the shortfall and its value-at-risk at level $1-\alpha$ at time t, respectively.

Financial markets

Vector auto-regressive model

When there is predictability in equity returns, a long-term investor such as a defined-benefit pension fund manager allocates more pension wealth to equities (Barberis 2000; Campbell et al. 2003). We use a vector auto-regressive (VAR) model to model predictability. Ferstl and Weissensteiner (2011) combine the VAR model with the Nelson-Siegel yield curve fitting function, as proposed by Boender et al. (2008). The Nelson-Siegel yield curve model is parsimonious and is known to reduce over-fitting and to return better out-of-sample predictions than affine term structure models (Diebold and Li 2006). Owadally et al. (2021) use the Nelson-Siegel model for both nominal and real yield curves, but two different nominal yield curves are modelled here. The s-year Treasury spot rate at time t is given:

$$\begin{aligned} y(\beta _t,s, \lambda ) \;=\; \beta _{1,t} \,+\, (\beta _{2,t}+\beta _{3,t}) \left( \frac{1-e^{-\lambda s}}{\lambda s} \right) \,-\, \beta _{3,t} e^{-\lambda s}, \end{aligned}$$

(2)

where $\beta _t=\left[ \beta _{1,t},\beta _{2,t},\beta _{3,t} \right] '$ is a time-varying parameter and where the scaling parameter $\lambda$ is a constant. Parameters are estimated by fitting the model above to historical Treasury yield curve data.² Pension liability valuation is based on a separate discount curve. The pension discount yield curve is also defined with Nelson-Siegel discount rate $y(\beta _t^P,s,\lambda ^P )$ and with corresponding parameters $\beta _t^P=[\beta _{1,t}^P,\beta _{2,t}^P,\beta _{3,t}^P ]'$ and $\lambda ^P$. The parameters are estimated by using FTSE pension discount curve data.³ This discount curve is constructed from high-quality corporate bond yields, which are not merely level-shifted Treasury bond yields (Duffee 1998). The Nelson-Siegel parameters are then applied to a VAR model given by

$$\begin{aligned} z_t = \Phi _0 + \Phi _1 z_{t-1} + v_t, \end{aligned}$$

(3)

where $z_t = [r_{1,t},r_{2,t},\ldots ,\pi _t, \beta _{1,t},\beta _{2,t},\beta _{3,t},\beta _{1,t}^P,\beta _{2,t}^P,\beta _{3,t}^P]'$. Here, $r_{i,t}$ is the realised log-return of an asset (class or fund) i over one month ending at time t, and $\pi _t$ is inflation over the month to time t. In Eq. (3), $\Phi _0$ is a column vector, $\Phi _1$ is a matrix of the slope coefficients of the VAR model, and $v_t$ is a column vector of normal iid innovations.

Table 4 in Appendix 1 shows the coefficients of the VAR model based on historical monthly data from July 2008 to May 2019. The variables $r_{1,t}$, $r_{2,t}$, ...$r_{6,t}$. denote, respectively, log-returns on S &P 500, Bloomberg-Barclays US Aggregate Bond, FTSE EPRA Nareit US, FTSE Global Core Infrastructure, S &P Global Timber and Forestry, NASDAQ AMX Global Agriculture. Compared to a similar model estimated by Barberis (2000), our estimated model features slightly higher predictability in equity returns ($R^2$ values are around 0.15 to 0.20) because lower interest rates coincide with higher equity returns in the data after the 2008 global financial crisis.

Figure 2a depicts the Treasury yield curve and pension discount curve at the steady state of the estimated VAR model. (Statistics for the variables at the steady state are shown in Table 5 in Appendix 1.) The yield and pension discount curves are upward-sloping, with the pension discount curve being at a higher level than the Treasury curve, capturing credit risk. In order to visualise the relationship between expected equity returns and the two yield curves, we simulate 10,000 values, plot expected equity returns versus short-term interest rates, and fit straight lines in Fig. 2b. The negative slope confirms the stylized fact that stock prices are expected to increase in a low short-term interest rate environment. Finally, Table 6 in Appendix A summarises conditional mean, standard deviation, and correlation coefficient values of the cumulative VAR variables over one year, starting from the steady state level presented in Table 5.

Fig. 2

Yield curves and expected equity returns

Asset pricing model

The set of financial assets is denoted by $\mathcal {I} \in \{1,2,\ldots ,N\}$. Among these assets, the subset of real illiquid assets is denoted by $\mathcal {R} \subset \mathcal {I}$. The real illiquid assets are property, infrastructure, timber & forestry, and agriculture. Let $\Delta t$ be the time interval between two consecutive times at which the portfolio is rebalanced; this may be one year or longer. Defining $R_{i,t}$ as the gross return of asset i over $\Delta t$ from time $t-\Delta t$ to t, the price $S_{i,t}$ of asset i evolves according to the following, given the initial price of asset i:

$$\begin{aligned} S_{i,t}=S_{i,t-\Delta t} \cdot R_{i,t}. \end{aligned}$$

(4)

For any given asset i whose returns are captured by our VAR model, the gross return is easily computed from the monthly log-returns given by Eq. (3).

Following Owadally et al. (2021a), the gross interest rate from time $t - \Delta t$ to t on the cash account or T-bill (indexed using $i=7$) is given by

$$\begin{aligned} R_{i,t} = \exp \left[ \Delta t \cdot y(\beta _{t-\Delta t}, \Delta t,\lambda )\right] . \end{aligned}$$

(5)

In addition, we consider two dynamic bond portfolios which are notional liability-hedging vehicles that are commonly used in practice: the first implements a duration-convexity matching strategy (Inglis et al. 2013) and the second follows a key-rate duration-matching strategy (Tuckman 2002, p. 133). The duration-convexity matching strategy involves immunization, that is rebalancing a bond portfolio such that the duration of the bond portfolio is equal to that of the pension liability, and the convexity of the bond portfolio is greater or equal to that of the pension liability. We assume that the returns on the duration-convexity matching fund at time t can be approximated by the returns on two zero-coupon bonds of maturities $M_{S,t}$ and $M_{L,t}$, respectively, shorter and longer than the maturity of the pension liability. The exact maturities and the number $\alpha _{S,t}$ and $\alpha _{L,t}$ of units of these two bonds are chosen by matching their duration to the duration of the pension liability, and by selecting their convexity so as to be closest to, but greater than, the convexity of the pension liability. The return on the duration-convexity matching fund from time $t-\Delta t$ to time t is

$$\begin{aligned} \begin{aligned} R_{DC,t}&=\alpha _{S,t} \cdot \exp \left[ M_{S,t} \cdot y\left( \beta _{t-\Delta t }^P,M_{S,t}, \lambda ^P\right) - \left( M_{S,t}-\Delta t\right) \cdot y\left( \beta _t^P,M_{S,t} -\Delta t,\lambda ^P\right) \right] \\&\quad + \alpha _{L,t} \cdot \exp \left[ M_{L,t} \cdot y\left( \beta _{t-\Delta t}^P,M_{L,t},\lambda ^P\right) - \left( M_{L,t}-\Delta t\right) \cdot y\left( \beta _t^P,M_{L,t}-\Delta t, \lambda ^P\right) \right] . \end{aligned} \end{aligned}$$

(6)

Note that the duration-convexity matching fund may fail to replicate changes in the pension liability, especially when the pension discount curve shifts in a non-parallel way, as is well known from the theory of immunization.

We also construct a bond portfolio using the key-rate duration-matching strategy, which is described in detail by Tuckman (2002, p. 133). This strategy is used by bond portfolio managers to cope with non-parallel shifts in the yield curve. Pension payment cash flows are defined on a discrete timeline. Given a set of zero-coupon bond maturities $\{M_{1,t},\ldots ,M_{K,t}\}$ at time t, we group the liability cash flows into baskets over the time intervals $(\tau _0,\tau _1 ],(\tau _1,\tau _2 ],\ldots ,(\tau _{K-1},\tau _K ]$ such that the duration of each cash flow basket is close to the maturity of a corresponding zero-coupon bond. Then, the key-rate duration-matching fund is constructed by weighting the zero-coupon bonds by the present value of each basket, giving the number $\alpha _{k,t}$ of units of k-year zero-coupon bond held in the fund. The return of this fund for time $t-\Delta t$ to time t is

$$\begin{aligned} R_{KD,t}=\sum _{k=1}^K \alpha _{k,t} \cdot \exp \left[ M_{k,t} \cdot y\left( \beta _{t-\Delta t}^P,M_{k,t},\lambda ^P\right) - \left( M_{k,t} - \Delta t\right) \cdot y\left( \beta _t^P,M_{k,t} - \Delta t, \lambda ^P\right) \right] . \end{aligned}$$

(7)

Optimization problem: multi-stage stochastic programming

Based on the market model in Sect. 3, we generate a scenario tree and formulate a multi-stage stochastic programming problem. See Barro et al. (2022), Consigli et al. (2017), Carpentier et al. (2015), and Birge and Louveaux (2011) for more details on stochastic programming. Let $\mathcal {N}$ be the set of all nodes in the tree, and $\mathcal {N}_t$ be the set of nodes at time t. The root node of the scenario tree is denoted by $n_0$. A notional example of a scenario tree appears in Fig. 3. For this pension portfolio problem, the end of the planning horizon at time T is the terminal stage. Thus, $\mathcal {N}_0=\{n_0\}$ contains the root node only, $\mathcal {N}_T$ is the set of leaf nodes, and $\mathcal {N}=\bigcup _{t \in [0,T]} \mathcal {N}_t$. A non-root node $n \ne n_0$ will branch off a parent node, denoted by $n^-$. A non-leaf node $n \notin \mathcal {N}_T$ has children nodes denoted by $n^+$.

Fig. 3

A notional example of a scenario tree with a root node $n_0$ capturing initial conditions

Cash balance constraints

Equations (8) and (9) below control cash inflows and outflows. The notation transfers straightforwardly from bearing a time t subscript to a node n subscript. For example, $C_n$ represents the contribution paid into the pension fund at node n. Furthermore, $X_{i,n}^{buy}$ and $X_{i,n}^{sell}$ are the number of units of asset i, priced at $S_{i,n}$, that are bought and sold, respectively, at node n, while $\varphi _i^s$ and $\varphi _i^u$ indicate a percentage selling fee and upfront fee, respectively, for each asset i. For example, if the manager decides to sell some units of a real asset, then she pays a ‘penalty’ of $\varphi _i^s=7.5\%$. The pension payment $P_n$ at node n is a static cash flow before buyout. At the buyout stage ($n \in \mathcal {N}_T$), $V_{i,n}$ is pre-scheduled selling transaction of a real asset $i \in \mathcal {R}$, and $B_n$ is the discounted value of projected pension payments based on Treasury yields.

$$\begin{aligned}&C_n + \sum _{i \in \mathcal {I}} X_{i,n}^{sell} S_{i,n} \left( 1-\varphi _i^s\right) + \sum _{i \in \mathcal {R}} V_{i,n} = \sum _{{i \in \mathcal {I}}} X_{i,n}^{buy} S_{i,n} \left( 1+\varphi _i^u\right) + P_n&\quad \text {for} \ n \in \mathcal {N} \setminus \mathcal {N}_T, \end{aligned}$$

(8)

$$\begin{aligned}&C_n + \sum _{{i \in \mathcal {I}}} X_{i,n}^{sell} S_{i,n} \left( 1-\varphi _i^s\right) + \sum _{i \in \mathcal {R}} V_{i,n} = B_n&\quad \text {for} \ n \in \mathcal {N}_T. \end{aligned}$$

(9)

Asset inventory constraints

Equation (10) below tracks the number $X_{i,n}$ of units of asset i held at node n. The percentage management fee for asset i is denoted by $\varphi _i^m$. Now, a real illiquid asset is subject to a steep liquidity penalty if the asset is sold immediately. Furthermore, full liquidation may not be practical immediately and we capture this by allowing for decisions to sell various units of the real asset in a deferred manner, over the next three time steps.

Thus, a decision is made at node n to sell $X_{i,n}^{sell}$ units of asset i immediately, as well as $X_{i,n,n^+}^{sell}$ units at the next time step, $X_{i,n,n^{++}}^{sell}$ after two time steps, and similarly for $X_{i,n,n^{+++}}^{sell}$, see Fig. 4. For non-real assets, e.g. stocks and bonds, there is no deferred liquidity penalty and $X_{i,n,n^+}^{sell}, X_{i,n,n^{++}}^{sell}$, and $X_{i,n,n^{+++}}^{sell}$ are set to zero.

$$\begin{aligned} X_{i,n}=X_{i,n^-} \left( 1-\varphi _i^m\right) + X_{i,n}^{buy}-\left( X_{i,n}^{sell}+X_{i,n,n^+}^{sell}+X_{i,n,n^{++}}^{sell}+X_{i,n,n^{+++}}^{sell}\right) \quad \text {for} \ n \in \mathcal {N}, \end{aligned}$$

(10)

Fig. 4

Deferred selling matrix for transactions in illiquid real assets

Figure 5 shows the deferred liquidity penalty over time, highest at 7.5% when liquidating a real asset immediately, but decreasing linearly all the way to 0% if the sale is delayed by three time steps. The pension fund manager can choose, at time t, corresponding to node n, how many units of an illiquid real asset to sell over the next time steps. The matrix in Fig. 4 shows the schedule of delayed transactions of real asset i at future nodes $n^+$, $n^{++}$ , and $n^{+++}$. To secure the scheduled selling amounts, we utilise an account $X_{i,n}^{sch}$ in Eq. (11).

Fig. 5

Deferred liquidity penalty faced when deciding, at time t, to sell an illiquid real asset at times t,$t+1$,$t+2$,$t+3$ in the future

$$\begin{aligned} X_{i,n}^{sch} = \left( X_{i,n,n^+}^{sell}+X_{i,n,n^{++}}^{sell}+X_{i,n,n^{+++}}^{sell} \right) + \left( X_{i,n^-,n^+}^{sell}+X_{i,n^-,n^{++}}^{sell} \right) + X_{i,n^{--},n^+}^{sell} \end{aligned}$$

(11)

At node n, the selling value $V_{i,n} \ge 0$ for pre-scheduled transactions of a real asset i is as follows:

$$\begin{aligned} V_{i,n}=X_{i,n^-,n}^{sell} S_{i,n} \left( 1-\varphi _{i,1}^s\right) + X_{i,n^{--},n}^{sell} S_{i,n} \left( 1-\varphi _{i,2}^s\right) +X_{i,n^{---},n}^{sell} S_{i,n} \left( 1-\varphi _{i,3}^s\right) , \end{aligned}$$

(12)

where the early redemption penalties $\varphi _{i,1}^s$, $\varphi _{i,2}^s$, and $\varphi _{i,3}^s$ are 5.0%, 2.5%, and 0.0%, respectively. These should be contrasted to the immediate redemption penalty $\varphi _i^s$ in Eqs. (8) and (9) of 7.5%. These values are depicted in Fig. 5.

Variable constraints

No short-selling is allowed as enforced in Eq. (13) below.⁴ Equations (14) and (15) mean that, at the end of the planning horizon, the pension portfolio is not allowed to buy more assets, and only allowed to sell holding assets to make a buyout deal.

$$\begin{aligned} C_n,X_{i,n},X_{i,n}^{buy},X_{i,n}^{sell},X_{i,n,m}^{sell},X_{i,n}^{sch} \ge 0&\quad \text {for} \ n \in \mathcal {N} \setminus \mathcal {N}_T \ \text {and} \ m \in \{n^+,n^{++},n^{+++}\}, \end{aligned}$$

(13)

$$\begin{aligned} C_n,X_{i,n},X_{i,n}^{sell} \ge 0&\quad \text {for} \ n \in \mathcal {N}_T, \end{aligned}$$

(14)

$$\begin{aligned} X_{i,n}^{buy},X_{i,n}^{sch}=0&\quad \text {for} \ n \in \mathcal {N}_T, \end{aligned}$$

(15)

Other constraints

The total asset value $A_n \ge 0$ of the pension fund before rebalancing satisfies Eq. (16).

$$\begin{aligned} A_n = \sum _{i \in \mathcal {I}} X_{i,n^-} S_{i,n} \left( 1-\varphi _i^m\right) + \sum _{i \in \mathcal {R}} X_{i,n^-}^{sch} S_{i,n} \left( 1-\varphi _i^m\right) \quad \text {for} \ n \in \mathcal {N}, \end{aligned}$$

(16)

where $\varphi _i^m$ indicates management fee for asset i. Also, an auxiliary Eq. (17) calculates the total asset value $\widetilde{A}_n$ after contribution, benefit payment, and rebalancing the portfolio.

$$\begin{aligned} \widetilde{A}_n = \sum _{i \in \mathcal {I}} X_{i,n} S_{i,n}+\sum _{i \in \mathcal {R}} X_{i,n}^{sch} S_{i,n} \quad \text {for} \ n \in N. \end{aligned}$$

(17)

Numerical results: simulations

We consider a benchmark case, in which the initial funding ratio of the pension portfolio is 85% before making contribution and pension payment. 60% of the pension fund wealth is invested in equities, and the rest is invested in an aggregate bond index-tracking fund. We begin with the case where we impose fixed contributions at a rate of 13% of the initial deficit for seven years.⁵ Other parameter values are given in Table 1.

Table 1 Parameter values for the benchmark case

In order to test the optimal investment strategy of the multi-stage stochastic programming model described in the previous section, we design a 10-year rolling horizon simulation (Kouwenberg 2001). At each simulated point every year, we solve the stochastic optimization problem and implement the initial solution. The generated scenario tree at each time step is based on the simulated point. This is then rolled forward to the next time step and the optimization is performed similarly. This is a form of receding horizon control, also known as model predictive control (Kwon and Han 2006).

Scenario tree generation follows the method described by Owadally et al. (2021a). Scenario trees are arbitrage-free. We use the approach of Høyland and Wallace (2001) to sequentially generate sub-trees by matching their first four conditional moments in order to construct one large scenario tree. We also validate no-arbitrage opportunities and no-arbitrage bound among investment assets (Klaassen 2022; Geyer et al. 2014). To reduce computation time, the number of stages of each scenario tree is limited to five. Stages of increasing lengths are used with the time periods of the first two stages fixed at one year. Numerical results in this section are from 1,000 simulation paths over a 10-year planning horizon, i.e. 10,000 simulation points.

Bond portfolio choice

The most important decision for managing a defined-benefit pension fund is to choose a suitable liability-hedging vehicle or strategy. We consider three possible bond portfolios for this purpose: an Aggregate Bond index-tracker, a Duration-Convexity matching portfolio, and a Key-Rate Duration-matching portfolio. These were described in Sect. 3.2.

Table 2 shows the tracking error of each bond portfolio. This measure is calculated as the sample standard deviation (volatility) of the difference between annual changes in the pension liability and the value of the bond portfolio over a 10-year planning horizon. A tracking error of zero would mean that the assets and the liabilities tracked each other perfectly over the planning horizon. The “Aggregate Bonds” index-tracking portfolio presents the highest tracking error. The “Key-Rate Duration” portfolio achieves the lowest tracking error.⁶

Table 2 Tracking errors of three bond portfolios

This clearly shows that adopting a bond strategy which hedges the unrewarded interest rate risk inherent in the liability can lead to a dramatic reduction in funding volatility, compared with the more passive approach like the “Aggregate Bonds” strategy.

Results without real assets

In order to investigate the effects of the different bond portfolios on optimal asset allocations, we limit the investment universe to T-bills, equities, and one of the three bond portfolios. Figure 6 shows the average optimal asset allocations over the 10-year planning horizon. Panel 6a “Liability” shows the average asset allocation when the bond portfolio is replaced with a hypothetical financial asset which perfectly matches the pension liability cash flows. This is introduced purely for comparative purposes. It is evident by visual inspection that the “Key-Rate Duration” matching strategy in panel 6d of Fig. 6 has the closest asset allocation shape to the hypothetical perfect case in panel 6a. The “Aggregate Bonds” index-tracking strategy in panel 6b and the “Duration Convexity” matching strategy in panel 6c both assign less wealth to the bond portfolio than the “Key-Rate Duration” strategy, because these two cases provide poorer hedges to the pension liability, as demonstrated by the tracking errors in Table 2.

Fig. 6

Average optimal portfolio allocations with different types of bond portfolios in the absence of real assets

It is also clear from Fig. 6 that there is a gradual decline in the allocation to equities. With the “Aggregate Bonds” strategy in Fig. 6b, at the start of the planning period, the investor allocates 77.6% on average to equities; by the end of the planning period the expected allocation to equities falls to 50.3%. The scheme is de-risking dynamically over time. The same holds for the Duration-Convexity matching strategy in panel 6c and for Key-Rate Duration-Matching in panel 6d. The average allocation to equities gradually reduces and the fixed income asset class increases.

We now compare the performance of the different liability-hedging strategies by investigating funding ratios, buyout cost, and risk measures, such as shortfall value-at-risk and expected shortfall. Figure 7 shows probabilities that the funding ratio at the end of each year is greater than 0.9, which is the lower point of a target range between 0.9 and 1.1. The key-rate duration-matching portfolio produces the closest probabilities over time to those of the hypothetical perfect liability-hedging asset. The aggregate bond index-tracking strategy consistently incurs the lowest probabilities, except in the first year.

Fig. 7

Probability of funding ratio in excess of 0.9 with LDI under various bond strategies in the absence of real assets

Figure 8 shows the cumulative buyout probability, i.e. the probability that the total value of the pension fund is greater than 70% of the buyout cost plus liability value, so that the sponsor is willing to pay 30% of the buyout cost on top of the pension fund. On a course towards the buyout at year 10, the aggregate bonds and duration-convexity matching portfolios are initially more likely than the key-rate duration-matching portfolio to lead to successful buyout. However, by year 10, the key-rate duration-matching portfolio outperforms the other two strategies and achieves a higher probability of buyout.

Fig. 8

Cumulative buyout probability with LDI under various bond strategies in the absence of real assets

In addition, we present sample statistics of the buyout cost with the three different bond portfolios in Table 3. The average and median cost with the key-rate duration-matching portfolio is 5% to 25% lower compared to the duration-convexity matching portfolio and the aggregate bond index-tracking portfolio. It also exhibits the lowest cost volatility.

Table 3 Buyout cost at the end of Year 10 with LDI under various bond strategies in the absence of real assets

In Fig. 9, we examine downside risk measures: the value-at-risk of shortfall, and the expected shortfall. (Recall that the shortfall is the pension fund deficit or the excess of liability over assets.) These risk measures are constrained as shown in Sect. 2.2. The key-rate duration-matching portfolio delivers the lowest values of value-at-risk and expected shortfall. Interestingly, the optimal solution with the aggregate bond index-tracking strategy exhibits increasing downside risk over time, while the other strategies exhibit decreasing or stable downside risk after year 1.

Fig. 9

Downside risk measures

The optimal LDI portfolio is stochastic and dynamic. To acquire greater intuition as to its structure and evolution, we perform a linear regression of simulated optimal LDI portfolios, with key-rate duration-matching, on various explanatory variables. This shows that the optimal LDI portfolio is highly sensitive to the long-term and short-term pension discount rates, but much less so to equity returns. This analysis is set out in B.

Effects of real assets

In the absence of real assets, we find that the key-rate duration-matching bond portfolio is the best hedge vehicle to achieve the three objectives, subject to the downside risk constraint, as described in the preceding section. In this section, we now reintroduce the full asset universe with the three liability-hedging strategies and we investigate the effects of real assets on optimal asset allocations, objectives, and risk measures. To capture illiquidity, the linear penalty rule featured in Fig. 5 is implemented in the model as the constraint given by Eq. (12). We consider four real asset classes: US real estate, global infrastructure, global timber, and global agriculture, with and without the linear penalty rule.

Real assets as a diversifying asset class

Figure 10 shows average asset allocations from the numerical results using the receding horizon control method. In the top two panels, the aggregate bond index-tracker bond portfolio is used, without real assets (panel 10a) and with real assets (panel 10b). In the bottom two panels, the key-rate duration-matching bond portfolio is used, again without and with real assets. The left panels of Fig. 10 are reproduced from Fig. 6, for convenience. Comparing the left and right panels in Fig. 10, we observe that, when real assets are available, significant investments are made in infrastructure and real estate at the expense of equity investment, on average. This is true both with the aggregate bond portfolio and with the key-rate duration-matching bond portfolio, but it is more notable in the former, presumably because a poorer hedge to the pension liability is achieved with an aggregate bonds passive strategy than with key-rate duration-matching.

Fig. 10

Average optimal portfolio allocations with and without real assets. When real assets are available, a deferred liquidity penalty is incurred as described in Fig. 5

Figure 10 suggests that real assets play a role in diversifying overall allocations away from equities over the 10-year period. Table 6 in Appendix 1 shows that the risk-reward profile for equities, real estate, and infrastructure are comparable. The mean and standard deviation of gross annual returns for equities are 8.75% and 16.43% resp., while for real estate they are 4.5%, 28.96% resp., and for infrastructure they are 8.12%, 13.67% resp. Figure 11a presents the Sharpe ratios, using the gross annual returns, over the years and for different asset classes: equities and infrastructure are notably similar in their risk-adjusted return. More importantly, Table 6 in Appendix 1 shows that the correlation coefficient of these returns with the long-term pension discount rate $\beta _{1,t}^P$ is positive and of a similar size: 40.79%, 38.14%, 43.82% for equities, real estate, and infrastructure. Figure 11b explores these correlations over time. Infrastructure and equity are similarly correlated to the short and long-term pension discount rates, especially at the start. The correlation between infrastructure and long-term rates falls in later years making infrastructure a more valuable diversifying asset class, relative to pension liabilities, than equity.

Fig. 11

Risk-adjusted returns and return correlation coefficients for different asset classes

The illiquidity of real assets

Real assets are illiquid. This means that either a hefty discount is incurred upon immediate liquidation, or sales have to be delayed. We have modelled illiquidity using the deferred liquidity penalty as depicted in Fig. 5. That is, an immediate sales fee of 7.5% of the value of the real asset is paid when it is sold straightaway, but the pension fund manager can also defer the sale and incur a lower selling fee (5.0%, 2.5%, 0.0% if deferring by 1 year, 2 years, and 3 years, respectively, as per Fig. 5). This should be compared with a sales fee of 0.5% for stocks and bonds and 0% for T-bills, as stated in Table 1. It is noteworthy that, in the right-hand panels of Fig. 10, real assets represent a significant portion of the optimal LDI pension portfolio in spite of the illiquidity and transaction costs.

It may be argued that the deferred liquidity penalty structure reduces the overall envelope of transaction costs on real assets by enabling deferral, and that this may therefore encourage purchase of real assets. To investigate this further, we compare the average optimal portfolio allocations with the deferred penalty (top two panels of Fig. 12) with the average optimal portfolios when there is only an immediate penalty of 7.5% and no deferral (bottom two panels of Fig. 12). The top two panels of Fig. 12 are reproduced from Fig. 10 for convenience and ease of comparison. We observe less average investment in real assets in the bottom panels of Fig. 12 compared to the top panels: the overall liquidity penalty is higher when sales cannot be delayed in exchange for lower sales fees. We also notice that, in the later years of LDI with key-rate duration-matching (panels 12b and d of Fig 12), the average investment in real assets is not markedly different whether real asset sales can be deferred with lower selling fees or not. This confirms that real assets have a part to play in liability-driven investment despite their illiquidity.

Fig. 12

Average optimal portfolio allocations with real assets. In the top two panels, we assume that real asset sales can be delayed subject to a “deferred liquidity penalty” as per Fig. 5. In the bottom two panels, lower sales fees are not available if sales are deferred (“immediate liquidity penalty”)

Risk and buyout with real assets

The illiquidity of real assets introduces a delay in investment decisions. When it is possible to defer the sales of real assets and achieve a lower transaction cost, buy and sell decisions concerning real assets must be made in advance. This is indeed observed in Fig. 12: in the top panels, average investment in real assets is made earlier than in the bottom panels. Illiquidity may therefore compel managers to make buy and sell decisions of real assets in advance and this could introduce sub-optimality and greater risk, compared to a situation where these assets were fully liquid.

Figures 13, 14, and 15 below extend Figs. 7, 8, and 9 in Sect. 5.2 and illustrate risk in our optimal LDI pension fund investment, with and without real asset investment, and with either an aggregate bond index-tracker portfolio or the key-rate duration-matching bond portfolio. Furthermore, we also allow for both an immediate liquidity penalty or a deferred liquidity penalty. We make the following observations:

• (1) LDI with the key-rate duration-matching bond portfolio is less risky than with the aggregate bond portfolio, whether real assets are available or not, especially in the later years. This is consistent with the results of Sect. 5.2 when real assets were absent, as shown in Figs. 7, 8, and 9.

• (2) When LDI includes real assets, and they are illiquid with a 7.5% liquidity penalty fee for selling immediately and no lower fees for deferred sales (“no linear penalty”), risk reduces compared to the situation where real assets are excluded. This risk reduction is not substantial but it is noteworthy that it occurs despite the selling fee for real assets being 15 times greater than for stocks and bonds.

• (3) When LDI includes real assets, and their illiquidity means that the pension fund manager makes trading decisions on real assets in advance (i.e. sales may be deferred so as to take advantage of lower sales fees later under the “linear liquidity penalty” fee structure), risk is higher than when real assets are absent. This is because of the lag created by illiquidity between decisions and transactions, as explained above.

Fig. 13

Probability of funding Ratio in excess of 0.9 with and without real assets, and with two different bond strategies (aggregate bond index-tracking, key-rate duration-matching). “Linear penalty” means that lower sales fees are available if real asset sales are delayed (deferred liquidity penalty as per Fig. 5). “No linear penalty” means that lower sales fees are not available if sales are deferred

Fig. 14

Cumulative buyout probability with and without real assets, and with two different bond strategies (aggregate bond index-tracking, key-rate duration-matching). “Linear penalty” means that lower sales fees are available if real asset sales are delayed (deferred liquidity penalty as per Fig. 5). “No linear penalty” means that lower sales fees are not available if sales are deferred

Fig. 15

Downside risk measures with and without real assets, and with two different bond strategies (aggregate bond index-tracking, key-rate duration-matching). “Linear penalty” means that lower sales fees are available if real asset sales are delayed (deferred liquidity penalty as per Fig. 5). “No linear penalty” means that lower sales fees are not available if sales are deferred

In conjunction with point (5.3) above, we conclude therefore that risk may or may not increase when real assets are held, depending on the precise effects of illiquidity. It must be reiterated that, in terms of the overall pension fund objectives, it is optimal to hold real assets when they are available, as demonstrated in Figs. 10 and 12.

Conclusion

We construct an optimal liability-driven investment (LDI) model for a defined-benefit pension scheme which is closed to new entrants. The pension fund invests in traditional liquid asset classes (Treasury bills, Treasury bonds, stocks) as well as real illiquid assets (infrastructure, real estate, forestry & timber, and agriculture). We assume that the pension scheme manager and sponsor seek to maximize funding ratios and minimize contributions over time, as well as minimize the buyout cost after 10 years. We formulate a time-additive objective function where risk preferences are piecewise linearized. Practical constraints such as no short-selling and a maximum amount of downside risk in terms of the pension fund deficit are incorporated. The stochastic asset universe is governed by a vector auto-regressive model including returns on all asset classes as well as Treasury bond yields and pension discount rates.

The model is solved numerically using the methodology of multi-stage stochastic programming. This is a flexible computational approach which can cope with a large number of state variables (several asset classes) and linear constraints (such as downside risk constraints). In particular, it enables us to model transaction costs and investment management fees. Real assets are relatively illiquid and we capture this by means of a deferred liquidity penalty structure: fees are high if an immediate sale is sought but they slide down linearly to zero if the sale is delayed.

Practical liability-driven investment (LDI) for pension funds uses one of a number of bond portfolio strategies. Our results show that an optimal LDI portfolio with the key-rate duration-matching bond strategy is superior to both a duration-convexity matching bond strategy and an aggregate bond index-tracker strategy. The key-rate duration-matching bond portfolio consists of zero-coupon bonds of various maturities which are matched, by duration, to pension liability cash flows grouped into bins or baskets. By contrast, the duration-convexity matching strategy seeks to immunize all of the pension liability, and we show that it has a higher tracking error than the key-rate duration-matching strategy. On average in the optimal LDI portfolio, equity investment declines while investment in the key-rate duration-matching bond portfolio increases, so that de-risking occurs. In the absence of real assets, we fit a linear regression to simulated optimal LDI strategies and demonstrate that the optimal LDI portfolio is highly sensitive to both the front and back ends of the pension discount curve, but much less so to equity returns.

When real assets are available, we show that the optimal LDI portfolio involves significant investment in these real assets, partially displacing equities. In particular, infrastructure and real estate enhance diversification in the LDI portfolio. Real asset investment is illiquid but our results hold despite assuming that selling real assets attracts a fee 15 times greater than when selling liquid assets such as stocks. If real asset sales are delayed because of their illiquidity, investment in real assets is brought forward on average in the optimal LDI portfolio. The lag between investment decisions and transactions caused by illiquidity creates higher downside risk, but it remains optimal to hold real assets in terms of the overall pension fund objectives.

Our model has limitations which require further study. The linear illiquidity penalty rule in Fig. 5 may not fully explain the illiquidity characteristics of real assets, although it represents an attempt to describe realistic deferred illiquid asset sales. Our numerical results are also based on the VAR parameters estimated with the data from 2008 to 2019. Longer periods as well as periods in different market regimes should be considered. As shown in Owadally et al. (2021), the numerical optimization is sensitive to VAR parameter estimates. An in-sample versus out-of-sample analysis would also test the robustness of the model to different market conditions. In order to avoid a heavy computational burden, the scenario trees used in our study are sparse so that optimal solutions are approximations. Recent stochastic programming techniques, such as approximate dynamic programming and stochastic dual dynamic programming, are being developed to overcome this issue for multi-period investment problems (Lee et al. 2023). Future work will address some of these issues.

Appendices

Appendix 1: Estimation result of the VAR model

See Tables 4, 5, and 6.

Table 4 VAR(1) parameters and t-statistics

Table 5 Steady-state mean ($\mu$), standard deviation ($\sigma$), and correlation values of the VAR variables

Table 6 Conditional mean, standard deviation, and correlation values of the cumulative VAR variables

Appendix 2: OLS regression results

The optimal asset allocation for the representative scheme is stochastic and involves a computational solution. The model finds the optimal allocation of scheme assets each year, given the scheme’s funding position at the end of each year and given the competing objectives of the pension scheme manager and sponsor. To demonstrate the intuition behind the optimal decisions, we perform a linear regression of the optimal asset allocation on the following explanatory variables: year, funding ratio, long-term discount rate, short-term discount rate, equity return, as well as various product terms; see Eq. (18). Table 7 shows the ordinary least square results, and the third column ignores variables which are not statistically significant.

$$\begin{aligned} \begin{aligned} \frac{X_{i,t} \cdot S_{i,t}}{\widetilde{A}_t}&= \ b_0 + b_1 \cdot t + b_2 \cdot \log \left( \frac{A_t}{L_t}\right) + b_3 \cdot \beta _{1,t}^P + b_4 \cdot \left( \beta _{1,t}^P+\beta _{2,t}^P\right) + b_5 \cdot R_{1,t} \\&\quad + b_6 \cdot t \cdot \log \left( \frac{A_t}{L_t}\right) + b_7 \cdot t \cdot \beta _{1,t}^P+b_8 \cdot t \cdot \left( \beta _{1,t}^P+\beta _{2,t}^P\right) + b_9 \cdot t \cdot R_{1,t} + e_i \end{aligned} \end{aligned}$$

(18)

Table 7 Regression coefficients, with standard error in parentheses, for full regression (OLS1) and for a regression on statistically significant variables only (OLS2)

In Fig. 16, we illustrate the sensitivity of these key variables to the optimal allocation in the case where the key-rate duration-matching bond portfolio is used. It is important to note that the allocation to the de-risking portfolio ranges from 20 to 40% throughout the planning period and that the bars in Fig. 16 are not cumulative, but instead represent sensitivities to these key variables. From Fig. 16, we observe that there is a time-varying effect of these explanatory variables on the optimal allocation to the de-risking portfolio change. For example, the optimal allocation changes by about 4% at the start of year 2 if there is a ten-percentage points increase (+ 10%p) in the funding ratio. However, the allocation sensitivity to the funding ratio decreases over time as the pension scheme becomes better funded on average and as the optimal investment in the de-risking portfolios increases on average. Overall, Fig. 16 shows that falling long-term interest rates should be associated with increasing allocations to the key-rate duration-matching portfolio. The opposite is true for a rise in short-term rates. This is because, as presented in Fig. 2b, lower short-term interest rates make equity investment more attractive and investment in bonds less attractive.

Fig. 16

Change in allocation to key-rate duration-matching portfolio for percentage changes in various explanatory variables

We can also see that it requires a much larger percentage increase in equity returns to change the allocation to the key-rate duration-matching portfolio. In other words, a one percentage point increase in the value of equities has only a small impact on the optimal allocation to the key-rate duration-matching portfolio. This particular result confirms how important interest rates are to the optimal asset allocation of a pension scheme, when the pension liability is taken into consideration. Note that the linear regression performed here is of an indicative nature only: the relationship between the explanatory variables and the optimal portfolio allocation dynamics is more complex and the impact of the variables will also be correlated.