Systematic extreme potential gain and loss spillover across countries

Abstract

This paper investigates the existence of systematic extreme risks at a multi-country level that leads to gains and losses spillover. A measure of systematic risk that quantifies both the downside risk and the upside potential in the extreme is introduced. This measure is based on the Conditional-Value-at-Risk (CoVaR) measure and copulas to capture dependencies. Using our approach, we study the contagion effect between different financial markets in the extreme. We show that there is an asymmetric contagion effect from the US stock market to other international markets. The impact is higher when the US market is extremely bear than when it is extremely bull. This paper adds novel findings on the asymmetry between extreme losses and extreme gains and the differences among different countries’ reactions to shocks.

Introduction

The risk-return trade-off is one of the fundamental topics in finance. It is more challenging to address this trade-off in the presence of the contagion effect between different financial markets. This paper analyzes the spillover effect of a given market on other markets in extreme good and extreme bad states. This analysis is based on an appropriate risk measure to evaluate extreme risks and an accurate model to capture dependencies between risks.

Traditionally, a rational investor maximizes their return while the risk is set at an acceptable level. Different models and frameworks were introduced to deal with the risk-return trade-off in the context of portfolio selection, asset allocation, and risk management. For instance, the mean-variance portfolio optimization suggested by Markowitz (1952) uses the variance as a risk measure, but such a measure does not provide enough information on the downside risk.

Based on Markowitz portfolio theory, other risk measures were introduced in finance, for example, Sharpe Ratio (Sharpe 1966), Sortino Ratio (Sortino and Price 1994), and the betas in the CAPM framework (Sharpe 1964). All these measures display some limitations in measuring extreme risks, and a new generation of risk measures was developed to quantify the tail behavior of financial risks starting with the introduction of the Value-at-Risk (VaR) and VaR-related measures such as the Tail-Value-at-Risk (TVaR).

A significant milestone in risk measures was presented by Artzner et al. (1997) through the concept of coherent risk measures that gives four axioms to follow by a given risk measure to feature some economic properties. In the past two decades, more research was dedicated to risk measurements, especially in the context of multivariate and dependent risks. In the context of portfolio allocation, rational investors are more sensitive to downside losses than upside gains, and an accurate risk measure should quantify this asymmetric behavior. Systematic and systemic risks attracted a lot of interest in the past few years, and many papers addressed measuring such risks. For instance, Rodriguez-Moreno and Pena (2013) estimate and compare macro and micro high-frequency market-based systemic risk measures using European and US interbank rates, stock prices, and credit derivatives. Puzanova and Dullmann (2013) assume that the banking system is modeled as a portfolio and measure systemic risk in terms of the expected shortfall of this portfolio.

This paper investigates the link between the downside risk and investment opportunities in the financial markets using a model that allows dependence between risks. Our framework is based on two main ideas: the presence of co-movements in the financial markets and the existence of systematic global risk. Equivalently, it is assumed that multiple risks are dependent, which leads to a co-movement in the extremes, i.e., the presence of both upper and lower dependencies. The idea of co-movements in the financial market means that the evolution of asset returns is subject to positive or negative dependence across assets and markets. Such movements are observed at different levels during crisis periods, during the pre-crisis, and post-crisis periods. Due to the co-movement phenomenon, an investor would consider an appropriate risk measure to evaluate both downside risk and the potential gain. The existence of these co-movements risks implicitly implies that the assets are supposed to be dependent, and any model should consider this dependence structure. On the other hand, systematic risk is the risk that one institution, sector, or a market would generate movement for the other assets, sectors, and markets.

Our framework aims to evaluate the impact of these co-movements due to a systematic risk on both the right tail, i.e., the extreme potential gain, and the left tail, i.e., the extreme downside risk. This proposed framework is based on a copula model that captures the dependencies between the risks and Conditional-Value-at-Risk (CoVaR) to measure the co-movements in the tails. The copula theory presents an exhaustive set of models to fit different types of dependence structures. These models gained extensive popularity in risk management and quantitative finance over the past few decades. For example, this theory is extensively valuable for studying default correlation in credit risk models, modeling operational risk, and determining the economic capital in insurance and finance. The CoVaR measures were introduced by Adrian and Brunnermeier (2011) to capture the distress spreading across financial institutions. These types of risk measures gained a lot of interest both in academia and industry in recent years. This interest significantly increases during periods of crisis and financial distress. The CoVaR measures are similar to the VaR measures except that the underlying distribution is conditional on a specific event. This feature makes the CoVaR more informative than the standard VaR measures in capturing extreme behavior. For instance, Capponi and Rubtsov (2022) use the CoVaR to derive optimal portfolios in the presence of a systematic risk. The CoVaR is also used by Brunnermeier et al. (2020) to decompose the banking systematic risk. This risk measure is also applied in the context of cryptocurrency markets (see Borri 2019) and in assessing the financial system vulnerability to fire sales (see Duarte and Eisenbach 2021). In many cases, the application of the CoVaR is combined with a copula-based model (see Karimalis and Nomikos 2018). Inspired by the CoVaR risk measures, other systematic risk measuring tools are introduced in the literature. For example, Brownlees and Engle (2017) introduce SRISK measure based on the Conditional Expected Shortfall measure(CoES) and Wang et al. (2017) use CAViaR to study extreme risks for financial institutions. We refer the reader to Benoit et al. (2017) and Feinstein et al. (2017) for more on measuring the systematic risk. In this paper, we use the idea of the conditional risk measure to evaluate the downside risk, but we extend it to quantify the potential gain. Two types of CoVaR measures are used: an Upper CoVaR and a Lower CoVaR to evaluate the impact of co-movements in the upper tails and lower tails, respectively. Based on these two measures, we define percentages of potential expected systematic extreme loss and extreme gain. These percentages would evaluate the impact of the systematic risk on each individual risks in both extremes (left tail and right tail).

To assess the spillover effect of extreme movements between stock returns, we first explore the response of different financial markets to extreme movements in the US market. In this paper, the analysis is focused on the following countries: Brazil, Canada, China, Germany, India, Japan, Russia, and the UK. Our results show that extreme negative shocks to the US financial market have a different effect on other markets than extreme positive shocks. The effect is also different across countries. For example, we show that conditional on the US financial Market, Brazil, Canadian German, India, and UK markets lose more when the US market is extremely bad. However, in the case of China, we observe that the Chinese market suffers both when the US market does extremely well or extremely bad. This observation suggests that there is an asymmetric spillover effect across countries. We also find that the potential expected systematic extreme loss percentage change and the potential expected systematic extreme gain percentage change are both higher during the crisis period and remain high in the post-crisis period for all countries except for the case of China, India, and Japan, where the gain is systematically decreasing during and after the crisis periods. This fact tests for the persistence of the contagion effect. In addition, we show that the presumption of the fact that the contagion effect is stronger for extreme negative returns than for extreme positive returns is in accordance with our findings. Bae et al. (2003)) find similar results. Following Kyle and Xiong (2001), we argue that the obtained results are the outcome of the financial intermediaries’ behavior. Kyle and Xiong (2001) state that ’When convergence traders¹ suffer trading losses, they have a reduced capacity for bearing risks. This fact motivates them to liquidate positions in both markets, resulting in reduced market liquidity, increased price volatility in both markets, and increased correlation. Through this mechanism, the wealth effect leads to contagion’. Yuan (2005) build a model of contagion and find similar results. Concerning policies, it is noteworthy to mention that our results provide a useful tool to predict which countries will suffer the most from any recession that may affect large economies in the post-Covid-19 crisis.

The framework presented in our paper helps investors who want to construct optimal global portfolios to measure the inter-connectivity between global markets. These investors wish to determine the existing opportunities and downside risks in their portfolios by measuring the tail dependencies between markets. Achieving successful portfolio management requires understanding how shocks in financial markets are propagated and how different markets respond under different types of shocks, good or bad. This understanding is done by extracting most of the available information about the interactions between stock markets. Considering these interactions is very important in risk hedging and portfolio allocation in the presence of systematic risk. Equipped with this understanding of the systemic risk and its extreme impacts, the investors transfer their funds from one market to another when they adjust their portfolios. The risk measures presented in this paper provide a better knowledge of the level of interdependencies between different stock markets due to the systematic risk. Therefore, quantifying the impact of this systematic risk offers the investor information to identify the current opportunities and risks in holding a global portfolio. It is also worth mentioning that our framework could be used to show the evolution of these interdependencies over time. This constitutes an essential tool for investors looking for a dynamic and diversified portfolio during stock market instability and growth. Our paper provides investors with a tool to identify the impact of systematic risk, which allows them to avoid extreme risks and benefit from extreme gains.

The rest of the paper is organized as follows. In “CoVaR risk measures” section, we present our extreme downside risk and the extreme upside potential measures. In “Split copulas” section, we define the new copula family used in the dependence modeling of returns. The formulas of our extreme risk and extreme potential measures are given in “CoVaR for split copulas” section. In “Specification of the marginal distributions and the copula” section, we specify the model of the marginal distributions of returns and the parametric copula family that we use in our illustration example. In Section 6, we provide an empirical application to illustrate the importance of our measures for modeling contagion effect across countries. A discussion of our empirical findings is presented in “ Discussion of results” section followed by concluding remarks in “Conclusion” section. The proofs of our theoretical results can be found in the appendix.

CoVaR risk measures

The CoVaR risk measure was first introduced by Adrian and Brunnermeier (2011). This risk measure aims to evaluate a financial institution’s contribution to systematic risk and its contribution to the risk of other financial institutions. In general, it is used to measure the marginal contribution of an institution against the overall systematic risk. However, such a measure could also be used to evaluate the impact of the whole market or the system on each individual institution. In this paper, we use the CoVaR risk measures to evaluate the dependence in the extremes between the systematic risk and the individual risks. The impact of the systematic risk should be captured through the co-movements in the upper and lower tails. In other words, two measurements are needed for both the upper and lower tails. For this purpose, we recall the definition of the CoVaR as proposed by Adrian and Brunnermeier (2011) and extended by Girardi and Ergün (2013). We call this version of CoVaR measure the lower CoVaR as it evaluates the co-movements in the left tail. Then, we define a new CoVaR-type measure for the right tail, called the upper CoVaR. The lower CoVaR provides a measurement of the downside risk in the distress periods while the upper CoVaR quantifies the potential gains in the growth periods.

Assume that for a given time t, $Y_{t}$ is the return of a given asset (it could also be a sector or an index). The most popular risk measure that financial institutions use to measure risks is the Value-at-Risk (VaR). Let $VaR_{\beta }(Y_{t})$ be the VaR for $Y_{t}$ at a certain confidence level $0\le \beta \le 1$. The measure $VaR_{\beta }(Y_{t})$ is defined as the $\beta$-quantile of the distribution of $Y_{t}$ and it is given by

$$\begin{aligned} Pr[Y_{t}\le VaR_{\beta }(Y_{t})]=\beta . \end{aligned}$$

(2.1)

Consider another random variable $X_{t}$ which could represent the return of another asset or the return of an index. In our framework, we are interested in the impact of $X_{t}$ on the distribution of $Y_{t}$ and how the tails of $Y_{t}$ behave given $X_{t}$. For this purpose, the risk measure CoVaR is used. For given confidence levels $\alpha$ and $\beta$, Adrian and Brunnermeier (2011) define the lower CoVaR risk measure, $CoVaR_{\alpha ,\beta }^{L}(Y_{t})$, as follows:

$$\begin{aligned} Pr[Y_{t}\le CoVaR_{\alpha ,\beta }^{L}(Y_{t})\mid X_{t}=VaR_{\alpha }(X_{t})]=\beta . \end{aligned}$$

(2.2)

The measure CoVaR proposed by Adrian and Brunnermeier (2011) assumes the conditioning on $X_{t}$ to be exactly at its VaR level. This definition of CoVaR has some limitations that have been discussed by Girardi and Ergün (2013) and Mainik and Schaanning (2014). One of the most significant drawbacks of this version is the absence of dependence consistency, as pointed out in Mainik and Schaanning (2014). A modified CoVaR measure is proposed by Girardi and Ergün (2013). The new definition of CoVaR is based on conditioning a stress event as its returns being at most at its VaR. The modified CoVaR is given by

$$\begin{aligned} Pr[Y_{t}\le CoVaR_{\alpha ,\beta }^{L}(Y_{t})\mid X_{t}\le VaR_{\alpha }(X_{t})]=\beta . \end{aligned}$$

(2.3)

The lower CoVaR, $CoVaR_{\alpha ,\beta }^{L}(Y_{t})$, is the VaR of $Y_{t}$ conditioning on $X_{t}$ being in financial distress. The risk measure $CoVaR_{\alpha ,\beta }^{L}(Y_{t})$ provides information about the conditional extreme downside risk. In order to quantify the impact of $X_{t}$ on the right tail of $Y_{t}$, an upper CoVaR risk measure is defined. This new measure evaluates the extreme potential gains for $Y_{t}$ given that $X_{t}$ is in extreme financial growth. For given confidence levels $\alpha$ and $\beta$, the upper CoVaR risk measure, $CoVaR_{\alpha ,\beta }^{U}(Y_{t})$, is given by

$$\begin{aligned} Pr[Y_{t}>CoVaR_{\alpha ,\beta }^{U}(Y_{t})\mid X_{t}>VaR_{\alpha }(X_{t})]=\beta . \end{aligned}$$

(2.4)

Assume that $X_{t}$ is the return of a market index and $Y_{t}$ is the return of a single asset in this market. Then, the two measures $CoVaR_{\alpha ,\beta }^{L}(Y_{t})$ and $CoVaR_{\alpha ,\beta }^{U}(Y_{t})$ provide a tool to evaluate how the returns $Y_{t}$ respond to the potential opportunities in the market, as well as the downside risk generated by distress in the whole market. Computing these two measures is very informative and shows how assets (or institutions) absorb the available information in the market. For further analysis of the extreme dependencies between $X_{t}$ and $Y_{t}$, the following ratios are defined:

$$\begin{aligned}&R_{\alpha ,\beta }^{L}=\frac{CoVaR_{\alpha ,\beta }^{L}\left( Y_{t}\right) -VaR_{\beta }^{L}(Y_{t})}{VaR_{\beta }^{L}(Y_{t})}, \end{aligned}$$

(2.5)

$$\begin{aligned}&R_{\alpha ,\beta }^{U}=\frac{CoVaR_{\alpha ,\beta }^{U}\left( Y_{t}\right) -VaR_{\beta }^{U}(Y_{t})}{VaR_{\beta }^{U}(Y_{t})}. \end{aligned}$$

(2.6)

Thus $R_{\alpha ,\beta }^{L}$ and $R_{\alpha ,\beta }^{U}$ are measures of the potential expected systematic extreme loss percentage change and the potential expected systematic extreme gain percentage change conditional on $X_{t}$ being in its extreme states. These two ratios could be used to identify the asymmetric behavior in the response of $Y_{t}$ to the movements of $X_{t}$.

In the rest of the paper, the extreme events are defined using the VaR risk measure. A market is said to be in an extreme bad state if the current return is below its VaR at a confidence level $\alpha$ with $\alpha =10\%,5\%,$ and $1\%$. Similarly, the market is said to be in an extreme good state if its current return is above its VaR at a confidence level $\alpha$ with $\alpha =90\%,95\%,$ and $99\%$.

In order to evaluate the upper and lower CoVaRs, one needs to determine the joint distribution of $X_{t}$ and $Y_{t}$. This distribution could be a non-parametric distribution (empirical distribution or kernel distribution), semi-parametric, or a fully-parametric distribution. One of our goals in this paper is to derive closed-from expressions for the ratios $R_{\alpha ,\beta }^{L}$ and $R_{\alpha ,\beta }^{U}$ and this implies the use of fully-parametric set-up. First, we assume that $(X_{t},Y_{t})$ has a copula C. Using Sklar’s theorem, the joint cumulative distribution function is given by

$$\begin{aligned} Pr\left( X_{t}\le x,Y_{t}\le y\right) =C(u,v), \end{aligned}$$

with $u=F_{X_{t}}(x)$ and $v=F_{Y_{t}}(y),$ where $F_{X_{t}}$ and $F_{Y_{t}}$ are the cumulative distribution functions for $X_{t}$ and $Y_{t}$, respectively. It follows that

$$\begin{aligned} Pr\left( Y_{t}\le y\mid X_{t}\le x\right) =\frac{C(u,v)}{u}. \end{aligned}$$

Then, (2.3) is equivalent to

$$\begin{aligned} \frac{C(\alpha ,F_{Y_{t}}\left[ CoVaR_{\alpha ,\beta }^{L}(Y_{t})\right] )}{ \alpha }=\beta . \end{aligned}$$

(2.7)

We also have

$$\begin{aligned} Pr\left( Y>y\mid X>x\right) =\frac{1-u-v+C(u,v)}{1-u}. \end{aligned}$$

Then, (2.4) is equivalent to

$$\begin{aligned} \frac{1-\alpha -F_{Y_{t}}(CoVaR_{\alpha ,\beta }^{U}(Y_{t}))+C(\alpha ,F_{Y}(CoVaR_{\alpha ,\beta }^{U}(Y_{t})))}{1-\alpha }=\beta . \end{aligned}$$

(2.8)

Split copulas

Sklar’s theorem (Sklar 1959) shows that any multivariate joint distribution can be decomposed into univariate marginal distributions and a copula, which fully captures dependence and co-movement. To fit the dependence in both the upper and the lower tails, the joint distribution of $(X_{t},Y_{t})$ is assumed to be given by the following copula:

$$\begin{aligned} {\mathbf {C}}_{SC}(u,v\mathbf {\shortmid }\theta _{1},\theta _{2})=\left\{ \begin{array}{lll} \tau {\mathbf {C}}_{1}\left( \left( \frac{u}{\tau }\right) ^{\kappa },v^{\kappa }\mathbf {\shortmid }\theta _{1}\right) ^{\frac{1}{\kappa }} &{} if &{} u\leqslant \tau \text { } \\ \tau v+\left( 1-\tau \right) {\mathbf {C}}_{2}\left( \left( \frac{u-\tau }{ 1-\tau }\right) ^{\kappa },v^{\kappa }\mathbf {\shortmid }\theta _{2}\right) ^{\frac{1}{\kappa }} &{} &{} Otherwise \end{array} \right. , \end{aligned}$$

where $\left( u,v\right) \in \left[ 0,1\right] ^{2},$ $0\leqslant \kappa \leqslant 1$ and $0<\tau <1$ with ${\mathbf {C}}_{1}$ and ${\mathbf {C}}_{2}$ are two given copulas. If ${\mathbf {C}}_{1}$ and ${\mathbf {C}}_{2}$ have a density and $0<\kappa \leqslant 1$ for $0<\tau <1$, then ${\mathbf {C}}_{\mathbf {SC}}\left( u,v\shortmid \theta _{1},\theta _{2}\right)$ is a copula.

The copula ${\mathbf {C}}_{\mathbf {SC}}$ can be rewritten as

$$\begin{aligned} {\mathbf {C}}_{\mathbf {SC}}\left( u,v\shortmid \theta _{1},\theta _{2}\right)= & {} \tau \left[ {\mathbf {C}}_{1}\left( \left( \frac{u}{\tau }\right) ^{\kappa },v^{\kappa }\mathbf {\shortmid }\theta _{1}\right) ^{\frac{1}{\kappa } }I_{u\leqslant \tau }\right] \\&\left( 1-\tau \right) \left[ \frac{\tau }{\left( 1-\tau \right) }v+{\mathbf {C}}_{2}\left( \left( \frac{u-\tau }{1-\tau }\right) ^{\kappa },v^{\kappa } \mathbf {\shortmid }\theta _{2}\right) ^{\frac{1}{\kappa }}(1-I_{u\leqslant \tau })\right] \end{aligned},$$

where $I_{u\leqslant \tau }=1$ if $u\leqslant \tau ,$ and $I_{u\leqslant \tau }=0$ otherwise. This form shows that the split copula can be written as a mixture of two truncated distributions.

We restrict ourselves to copulas ${\mathbf {C}}_{1}$ and ${\mathbf {C}}_{2}$ for which the copula densities exist and, consequently, the two-increasing condition is met if $\frac{d^{2}{\mathbf {C}}_{\mathbf {SC}}\left( u,v\shortmid \theta _{1},\theta _{2}\right) }{dudv}$ is non-negative, i.e., $\frac{d^{2}{\mathbf {C}}_{\mathbf {SC}}\left( u,v\shortmid \theta _{1},\theta _{2}\right) }{ dudv}\geqslant 0$.

Theorem 3.1

Let $u^{*}=\left( \frac{u-\tau }{1-\tau }\right) ^{\kappa },$ $v^{*}=v^{\kappa },$ and $u^{**}=\left( \frac{u}{\tau }\right) ^{\kappa }$ then ${\mathbf {C}}_{\mathbf {SC}}$ is a copula with the following density:

$$\begin{aligned} \mathbf {{\mathbf {c}}_{SC}}\left( u,v\shortmid \theta _{1},\theta _{2}\right) =\left\{ \begin{array}{lll} \begin{array}{l} \kappa \frac{u^{\kappa -1}}{\tau ^{\kappa -1}}v^{\kappa -1}{\mathbf {C}} _{1}\left( \frac{u^{\kappa }}{\tau ^{\kappa }},v^{\kappa }\mathbf {\shortmid } \theta _{1}\right) ^{\frac{1}{\kappa }-2} \\ \left[ \left( \frac{1}{\kappa }-1\right) {\mathbf {C}}_{1,v^{*}}\left( \frac{u^{\kappa }}{\tau ^{\kappa }},v^{\kappa }\mathbf {\shortmid }\theta _{1}\right) {\mathbf {C}}_{1,u^{**}}\left( \frac{u^{\kappa }}{\tau ^{\kappa }},v^{\kappa }\mathbf {\shortmid }\theta _{1}\right) \right. \\ +\left. {\mathbf {C}}_{1}\left( \frac{u^{\kappa }}{\tau ^{\kappa }},v^{\kappa } \mathbf {\shortmid }\theta _{1}\right) {\mathbf {c}}_{1}\left( \frac{u^{\kappa } }{\tau ^{\kappa }},v^{\kappa }\mathbf {\shortmid }\theta _{1}\right) \right] \end{array} &{} \text {if} &{} u\leqslant \tau \\ &{} &{} \\ \begin{array}{c} \kappa v^{\kappa -1}\left( \frac{u-\tau }{1-\tau }\right) ^{\kappa -1} {\mathbf {C}}_{2}\left( \left( \frac{u-\tau }{1-\tau }\right) ^{\kappa },v^{\kappa }\mathbf {\shortmid }\theta _{2}\right) ^{\frac{1}{\kappa }-2} \\ \left[ \left( \frac{1}{\kappa }-1\right) {\mathbf {C}}_{2,v^{*}}\left( \left( \frac{u-\tau }{1-\tau }\right) ^{\kappa },v^{\kappa }\mathbf { \shortmid }\theta _{2}\right) {\mathbf {C}}_{2,u^{*}}\left( \left( \frac{ u-\tau }{1-\tau }\right) ^{\kappa },v^{\kappa }\mathbf {\shortmid }\theta _{2}\right) \right. \\ +\left. {\mathbf {C}}_{2}\left( \left( \frac{u-\tau }{1-\tau }\right) ^{\kappa },v^{\kappa }\mathbf {\shortmid }\theta _{2}\right) {\mathbf {c}}_{2}\left( \left( \frac{u-\tau }{1-\tau }\right) ^{\kappa },v^{\kappa }\mathbf { \shortmid }\theta _{2}\right) \right] \end{array}&\,&Otherwise \end{array} \right\} , \end{aligned}$$

where ${\mathbf {C}}_{i,u}\left( u,v\mathbf {\shortmid }\theta _{i}\right) = \frac{d\mathbf {{\mathbf {C}}_{i}}\left( u,v\shortmid \theta _{1},\theta _{2}\right) }{du},$ ${\mathbf {C}}_{i,v}\left( u,v\mathbf {\shortmid }\theta _{i}\right) =\frac{d\mathbf {{\mathbf {C}}_{i}}\left( u,v\shortmid \theta _{1},\theta _{2}\right) }{dv},$ and ${\mathbf {c}}_{i}\left( u,v\mathbf { \shortmid }\theta _{i}\right) =\frac{d^{2}\mathbf {{\mathbf {C}}_{i}}\left( u,v\shortmid \theta _{1},\theta _{2}\right) }{dudv}$ $(i=1,2)$.

To assess the tail dependence, we consider the coefficients of the upper, $\lambda _{U}$, and the lower ,$\lambda _{L}$, tail dependence (see Joe (1997)). For any given copula C we define

$$\begin{aligned} \lambda _{L}=\lim _{u\rightarrow 0}\frac{C(u,u)}{u}, \end{aligned}$$

(3.1)

and

$$\begin{aligned} \lambda _{U}=\lim _{u\rightarrow 1}\frac{{\overline{C}}(1-u,1-u)}{1-u}, \end{aligned}$$

(3.2)

where ${\overline{C}}$ is the survival copula and it is given by ${\overline{C}} (u,v)=u+v-1+C(1-u,1-v)$. The copula C has a lower (an upper) tail dependence if $\lambda _{L}$ $\in (0,1]$ ($\lambda _{U}$ $\in (0,1]$), and no lower (upper) tail dependence if $\lambda _{L}=0$ ($\lambda _{U}=0$).

CoVaR for split copulas

In this section, explicit formulas for CoVaR measures are obtained using the split copulas defined in the previous section. Recall that

$$\begin{aligned} {\mathbf {C}}_{SC}(u,v\mathbf {\shortmid }\theta _{1},\theta _{2})=\left\{ \begin{array}{lll} \tau {\mathbf {C}}_{1}\left( \left( \frac{u}{\tau }\right) ^{\kappa },v^{\kappa }\mathbf {\shortmid }\theta _{1}\right) ^{\frac{1}{\kappa }} &{} if &{} u\leqslant \tau \text { } \\ \tau v+\left( 1-\tau \right) {\mathbf {C}}_{2}\left( \left( \frac{u-\tau }{ 1-\tau }\right) ^{\kappa },v^{\kappa }\mathbf {\shortmid }\theta _{2}\right) ^{\frac{1}{\kappa }} &{} &{} Otherwise \end{array} \right. , \end{aligned}$$

(4.1)

where $\left( u,v\right) \in \left[ 0,1\right] ^{2},$ $0\leqslant \kappa \leqslant 1$ and $0<\tau <1$. Then ${\mathbf {C}}_{SC}$$(u,v\mathbf { \shortmid }\theta _{1},\theta _{2})$ is a copula. Note that the parameter $\kappa$ is a distortion parameter. We define the following copula:

$$\begin{aligned} {\mathbf {C}}_{i}^{(\kappa )}(u,v)={\mathbf {C}}_{i}\left( \left( u\right) ^{\kappa },v^{\kappa }\right) ^{\frac{1}{\kappa }}, \end{aligned}$$

(4.2)

for $i=1,2$.

Remark 4.1

Note that if ${\mathbf {C}}_{i}$ is an archimedean copula with a given generator $\phi _{i}$, then ${\mathbf {C}}_{i}^{(\kappa )}$ is also an archimedean copula with a generator $\psi _{i}(t)=\phi _{i}(t^{\kappa })$, for $i=1,2$.

Assume that $C=C_{SC}$ in (2.7) with $\alpha \le \tau$. Then,

$$\begin{aligned} \tau {\mathbf {C}}_{1}^{(\kappa )}\left( \frac{\alpha }{\tau },F_{Y_{t}}\left[ CoVaR_{\alpha ,\beta }^{L}(Y_{t})\right] \right) =\alpha \beta . \end{aligned}$$

(4.3)

Moreover, assume that ${\mathbf {C}}_{1}^{(\kappa )}$ is archimedean with a generator $\psi _{1}$, i.e.,

$$\begin{aligned} {\mathbf {C}}_{1}\left( u,v\right) =\psi _{1}^{-1}[\psi _{1}(u)+\psi _{1}(v)]. \end{aligned}$$

(4.4)

The assumption of working with archimedean copulas is very important in the context of this paper. First, the family of archimedean copulas is very riche and provides a lot of flexibility in terms of fitting dependence between rvs. Second, this assumption allows us to derive closed-form expression for the lower Covar risk measures as well as the ratio $R_{\alpha ,\beta }^{L}$. Indeed, combining (4.3) and (4.4) leads to

$$\begin{aligned} CoVaR_{\alpha ,\beta }^{L}(Y_{t})=F_{Y_{t}}^{-1}\left[ \psi _{1}^{-1}\left( \psi _{1}\left( \frac{\alpha \beta }{\tau }\right) -\psi _{1}\left( \frac{ \alpha }{\tau }\right) \right) \right] , \end{aligned}$$

(4.5)

where $F_{Y_{t}}^{-1}$ is the inverse cumulative distribution function of $Y_{t}$.

Similarly, let $C=C_{SC}$ in (2.8) with $\alpha >\tau$. Then,

$$\begin{aligned} 1-u-v+C_{SC}(u,v)= & {} 1-u-v+\tau v+\left( 1-\tau \right) {\mathbf {C}}_{2}\left( \left( \frac{u-\tau }{1-\tau }\right) ^{\kappa },v^{\kappa }\right) ^{\frac{1 }{\kappa }} \\= & {} (1-\tau )\left[ 1-\frac{u-\tau }{1-\tau }-v+{\mathbf {C}}_{2}^{(\kappa )}\left( \frac{u-\tau }{1-\tau },v\right) \right] \\= & {} (1-\tau )\mathbf {{\overline{C}}}_{2}^{(\kappa )}\left( \frac{1-u}{1-\tau } ,1-v\right) \end{aligned}$$

where $\mathbf {{\overline{C}}}_{2}^{(\kappa )}$ is the survival copula of ${\mathbf {C}}_{2}^{(\kappa )}$. Then,

$$\begin{aligned} (1-\tau )\mathbf {{\overline{C}}}_{2}^{(\kappa )}\left( \frac{1-\alpha }{1-\tau },1-F_{Y_{t}}\left[ CoVaR_{\alpha ,\beta }^{U}(Y_{t})\right] \right) =(1-\alpha )\beta . \end{aligned}$$

(4.6)

In order to find a closed-from for the upper CoVaR, we assume that the survival copula of ${\mathbf {C}}_{2}$ is archimedean with a generator $\phi _{2}$. This is equivalent to assume that $\mathbf {{\overline{C}}}_{2}^{(\kappa )}$ is archimedean with a generator $\psi _{2}(t)=\phi _{2}(t^{\kappa })$, i.e.,

$$\begin{aligned} \mathbf {{\overline{C}}}_{2}^{(\kappa )}\left( u,v\right) =\psi _{2}^{-1}[\psi _{2}(u)+\psi _{2}(v)]. \end{aligned}$$

(4.7)

Using (4.6) and (4.7), one finds

$$\begin{aligned} CoVaR_{\alpha ,\beta }^{U}(Y_{t})=F_{Y_{t}}^{-1}\left[ 1-\psi _{2}^{-1}\left( \psi _{2}\left( \frac{(1-\alpha )\beta }{1-\tau }\right) -\psi _{2}\left( \frac{1-\alpha }{1-\tau }\right) \right) \right] . \end{aligned}$$

(4.8)

For the split copulas, the lower and upper tail coefficients are given in terms of the copulas generators as follows:

$$\begin{aligned} \lambda _{L}=\lim _{u\rightarrow 0}\frac{\psi _{1}^{-1}\left( \psi _{1}\left( \frac{u}{\tau }\right) +\psi _{1}\left( u\right) \right) }{\frac{u}{\tau }}, \end{aligned}$$

and

$$\begin{aligned} \lambda _{U}=\lim _{u\rightarrow 1}\frac{\psi _{2}^{-1}\left( \psi _{2}\left( \frac{1-u}{1-\tau }\right) +\psi _{2}(1-u)\right) }{\frac{1-u}{1-\tau }}. \end{aligned}$$

It is important to note that a good choice of the generators $\psi _{1}$ and $\psi _{2}$ could lead to a good fit of both upper and lower dependence.

Specification of the marginal distributions and the copula

The marginal distributions

To model the marginal distributions, we use the two-piece exponential power distribution also called the split exponential power distribution. Another possible choice is the skewed t-distribution of Hansen (1994). We use the exponential power distribution instead of t-distribution because the latter allows only for fatter tails than the normal, while the former allows for both fat and thin tails and reduces to the normal distribution when the shape parameter is equal to 2. The exponential power distribution family (EP) has as a general form of the standardized density function from Rombouts and Bouaddi (2009) and Douch et al. (2015) that is defined for any real number x as

$$\begin{aligned} g(x)=\frac{\lambda }{2\sqrt{2}\Gamma (\frac{1}{\lambda })}\exp \left( -\left| \frac{x}{\sqrt{2}}\right| ^{\lambda }\right) , \end{aligned}$$

(5.1)

where $\lambda$ is the shape parameter. When $\lambda$ approaches 0 the distribution exhibits fat tails and when $\lambda$ tends to infinity the tails become tiny. The EP distribution has as special cases the normal $(\lambda =2)$ and Laplace $(\lambda =1)$. GED distribution is used in financial econometrics by Liesenfeld and Jung (2000) and Hardouvelis and Theodossiou (2002). Komunjer (2007) present an asymmetric extension of the exponential power distribution with applications to risk management.

While the EP family of distributions is appropriate for data with excess kurtosis, it is not useful for modeling data with significant skewness. To allow for skewness, we use the following asymmetric centered and scaled version of the EP distribution (hereafter SEP$(\mu _{t},\sigma _{1,t},\sigma _{2,t},\lambda )$)

$$\begin{aligned} f(r_{t})=k\frac{\lambda \exp \left( -(\frac{-\left( r_{t}-\mu _{t}\right) d_{t}}{\sqrt{2}\sigma _{1,t}})^{\lambda }-(\frac{\left( r_{t}-\mu _{t}\right) (1-d_{t})}{\sqrt{2}\sigma _{2,t}})^{\lambda }\right) }{2\sqrt{2} \Gamma (\frac{1}{\lambda })}, \end{aligned}$$

(5.2)

where the function $\Gamma (x)$ is the Gamma function given by

$$\begin{aligned}&\Gamma (x)=\int _{0}^{+\infty }t^{x-1}\exp \left[ -t\right] \mathrm{{d}}t, \\&k=\frac{2}{\sigma _{1,t}+\sigma _{2,t}}, \end{aligned}$$

and

$$\begin{aligned} d_{t}=\left\{ \begin{array}{c} 1 \ \ \text {if }r_{t}\leqslant \mu _{t} \\ 0 \ \ \text {Otherwise} \end{array} \right. . \end{aligned}$$

(5.3)

The density (5.2) can be rewritten in a two-piece form as

$$\begin{aligned} f(r_{t})=\frac{\lambda }{\sqrt{2}\Gamma (\frac{1}{\lambda })\left( \sigma _{1,t}+\sigma _{2,t}\right) }\left\{ \begin{array}{ccc} \exp \left( -\left| \frac{r_{t}-\mu _{t}}{\sqrt{2}\sigma _{1,t}}\right| ^{\lambda }\right) &{} \text {if} &{} r_{t}\leqslant \mu _{t} \\ \exp \left( -\left| \frac{r_{t}-\mu _{t}}{\sqrt{2}\sigma _{2,t}}\right| ^{\lambda }\right) &{} &{} \text {Otherwise} \end{array} \right. . \end{aligned}$$

(5.4)

The parameter $\mu _{t}$ is the conditional mode, the parameters $\sigma _{1,t}$ and $\sigma _{2,t}$ capture the dispersion (conditional volatilities) in bad and good regimes, respectively.

Theorem 5.1

The cumulative distribution function (CDF) and the quantile function of ( 5.2 ) are defined by

$$\begin{aligned} F(r_{t})=\left\{ \begin{array}{ccc} \frac{\sigma _{1,t}}{\sigma _{1,t}+\sigma _{2,t}}\left( 1-\gamma _{\mathrm{{inc}}}\left( \left| \frac{r_{t}-\mu _{t}}{\sqrt{2}\sigma _{1,t}}\right| ^{\lambda },\frac{1}{\lambda }\right) \right) &{} if &{} r_{t}<\mu _{t} \\ \frac{\sigma _{1,t}}{\sigma _{1,t}+\sigma _{2,t}}+\frac{\sigma _{2,t}}{ \sigma _{1,t}+\sigma _{2,t}}\gamma _{\mathrm{{inc}}}\left( \left| \frac{r_{t}-\mu _{t}}{\sqrt{2}\sigma _{2,t}}\right| ^{\lambda },\frac{1}{\lambda } \right) &{} &{} Otherwise \end{array} \right. , \end{aligned}$$

(5.5)

and

$$\begin{aligned} q_{t}=\left\{ \begin{array}{ccc} \mu _{t}-\sqrt{2}\sigma _{1,t}\left( \gamma _{inc}^{inv}\left( 1-\frac{ \sigma _{1,t}+\sigma _{2,t}}{\sigma _{1,t}}p\right) \right) ^{\frac{1}{ \lambda }} &{} if &{} p<\frac{\sigma _{1,t}}{\sigma _{1,t}+\sigma _{2,t}} \\ \mu _{t}+\sqrt{2}\sigma _{2,t}\left( \gamma _{inc}^{inv}\left( \frac{\sigma _{1,t}+\sigma _{2,t}}{\sigma _{2,t}}\left( p-\frac{\sigma _{1,t}}{\sigma _{1,t}+\sigma _{2,t}}\right) \right) \right) ^{\frac{1}{\lambda }} &{} &{} Otherwise \end{array} \right. , \end{aligned}$$

(5.6)

where the function $\gamma _{inc}\left( x\right)$ is the Gamma distribution CDF given by

$$\begin{aligned} \gamma _{inc}\left( x\right) =\frac{\int _{0}^{x}t^{x-1}\exp \left[ -t\right] \mathrm{{d}}t}{\Gamma (x)}. \end{aligned}$$

The function $\gamma _{inc}^{inv}$ is the quantile of Gamma distribution.

See the proof in Appendix A.

Specification of the location and scale parameters

To allow for time-varying conditional location and scale parameters of returns, we consider six different models: GARCH, AGARCH, EGARCH (Exponential GARCH), GJR (threshold GARCH), PARCH (Power ARCH), and the component GARCH. To select the best model among these six model, we use three commonly used information criteria: Schwartz Criterion, Akaike Criterion, and Hannan–Quinn Criterion. The obtained results are given in Tables 13, 14, and 15 in the appendix. Based on these tests, we select AGARCH. ARMAGARCH models become a work horse when it comes to modeling the financial time series dynamic. Financial time series usually include location and scale models. The location component is modeled using conditional mean models usually ARMA models. The scale component which is just the volatility of returns is modeled using GARCH model. The rational behind this choice is that financial time series have some dominant stylized facts such as volatility clustering, volatility persistence, asymmetric news effect, and fat tails. Volatility clustering and fat tails can have dramatic effect on the forecasting performance of the model. More specifically, ignoring volatility dynamics may lead to underestimating of risk measures such as value at risk. In order to achieve accurate forecast, most researchers apply GARCH to model volatility and autoregressive moving average (ARMA) to model the conditional mean. There is a consensus on families of GARCH(1,1) as the popular model among others specifications because it is sufficient to capture the volatility clustering in the data the simplest and most robust among volatility models on modeling studies have selected GARCH(1,1) model to analyze the dynamic of time series data. In our empirical application, we estimated GARCH models with different lag length and used the Bayesian information criterion to select the optimal model. We found that the best model is GARCH(1,1).

In this paper, this approach is adopted and the model for $\mu _{t}$ is an ARMA(1,1)

$$\begin{aligned} r_{t}=\mu _{t}\text { }+\varepsilon _{t}\text {,} \end{aligned}$$

where $r_{t}$ is the return of the stock at time t and

$$\begin{aligned} \mu _{t}=\mu +\phi r_{t-1}+\varphi \varepsilon _{t-1}\text {.} \end{aligned}$$

(5.7)

The model for $\sigma _{1,t}$ and $\sigma _{2,t}$ is an asymmetric GARCH(1,1) of Engle (1993), i.e., AGARCH(1,1) given by

$$\begin{aligned} \sigma _{i,t}^{2}=\sigma _{i}+\alpha _{i}(\varepsilon _{t-1}-\delta _{i})^{2}+\beta _{i}\sigma _{i,t-1}^{2}{ \ \ \ }\left( i=1,2\right) . \end{aligned}$$

(5.8)

The parameters $\alpha _{i},\ \beta _{i}$, and$\ \delta _{i}$ capture, respectively, the effect of news, the volatility persistence, and the leverage effect. For instance, if $\delta _{i}>0,$ then bad news have a higher effect on volatility than good news. This can be seen clearly by rewriting the variance equation as

$$\begin{aligned} \sigma _{i,t}^{2}=\sigma _{i}^{*}+\alpha _{i}\varepsilon {}_{t-1}^{2}-\alpha _{i}\delta _{i}\varepsilon {}_{t-1}+\beta _{i}\sigma _{i,t-1}^{2}{ \ \ \ }\left( i=1,2\right) , \end{aligned}$$

where $~\sigma _{i}^{*}=\sigma _{i}+\alpha _{i}\delta _{i}^{2}$ and $\delta _{i}^{*}=\alpha _{i}\delta _{i}$. Since $\delta _{i}^{*}$ is positive, bad news $\left( \varepsilon {}_{t-1}<0\right)$ have a higher effect on the volatility than good news $\left( \varepsilon {}_{t-1}>0\right)$. Notice that, because the distribution is asymmetric, $\mu _{t}$ is the conditional mode rather than the conditional mean.

Dependence specification

The split copulas introduced in “Split copulas” section could be defined using any copula family for $C_{1}$ and $C_{2}$. Also, the closed form for the CoVaR up and the CoVaR down as along as the copulas $C_{1}$ and $C_{2}$ are Archimedean copulas. In our numerical implementation, we have many choices for the copulas $C_{1}$ and $C_{2}$. Based on the ability of the Clayton copulas to capture extreme dependence and after testing the best fit using Schwartz Criterion, Akaike Criterion, and Hannan–Quinn Criterion, the Clayton copula was selected. For more details on the Clayton copulas, we refer to Joe (1997). In the case of Clayton copula, the distortion parameter $\kappa$ is not identified. Thus, it is normalized to $\kappa =1$. It follows that the split copula is defined by assuming that both $C_{1}$ and ${\overline{C}}_{2}$ to be Clayton copulas with parameters $\theta _{1}$ and $\theta _{2}$, respectively. For instance, the characteristics of this copula are given in Table 1.

Table 1 The main characteristics of Clayton copulas

The Clayton copula is a member of the Archimedean copula family. It has a dependence parameter $\left( -1,+\infty \right) \backslash \left\{ 0\right\}$ and generator function $\psi \left( u\right) =\frac{u^{-\theta }-1}{\theta }$. The perfect dependence is approached at $\theta \longrightarrow +\infty$, while independence is attained at $\theta \longrightarrow 0$. The Clayton copula is preferred for modeling positive dependence and asymmetric tail dependence in the lower tail. The lower and upper tail dependence coefficients for the split copula using (3.1) and (3.2) become

$$\begin{aligned} \lambda _{L}=(1+\tau ^{-\theta _{1}})^{-\frac{1}{\theta _{1}}}, \end{aligned}$$

and

$$\begin{aligned} \lambda _{U}=(1+(1-\tau )^{-\theta _{2}})^{-\frac{1}{\theta _{2}}}. \end{aligned}$$

Working with Clayton copulas allows us to obtain closed forms for CoVaR risk measures as well as introducing upper and lower tail dependence. These two features motivate the choice of the Clayton copula. Other copulas could be considered but our analysis is limited to the case of a split copula based on Clayton copulas. The density of split copula is given by

$$\begin{aligned} {\mathbf {C}}_{SC}(u,v\mathbf {\shortmid }\theta _{1},\theta _{2})=\left\{ \begin{array}{lll} \tau \left( \left( \frac{u}{\tau }\right) ^{-\theta _{1}}+v^{-\theta _{1}}-1\right) ^{-\frac{1}{\theta _{1}}} &{} if &{} u\leqslant \tau \text { } \\ u+v-1+\left( 1-\tau \right) \left( \left( \frac{1-u}{1-\tau }\right) ^{-\theta _{2}}+(1-v)^{-\theta _{2}}-1\right) ^{-\frac{1}{\theta _{2}}} &{} &{} Otherwise \end{array} \right. , \end{aligned}$$

(5.9)

and

$$\begin{aligned} {\mathbf {c}}_{SC}(u,v\mathbf {\shortmid }\theta _{1},\theta _{2})=\left\{ \begin{array}{lll} (\theta _{1}+1)\left( \frac{uv}{\tau }\right) ^{-(\theta _{1}+1)}(\left( \frac{u}{\tau }\right) ^{-\theta _{1}}+v^{-\theta _{1}}-1)^{-\frac{2\theta _{1}+1}{\theta _{1}}} &{} if &{} u\leqslant \tau \text { } \\ (\theta _{2}+1)\left( \frac{(1-u)(1-v)}{1-\tau }\right) ^{-(\theta _{2}+1)}\left( \left( \frac{1-u}{1-\tau }\right) ^{-\theta _{2}}+(1-v)^{-\theta _{2}}-1\right) ^{-\frac{2\theta _{2}+1}{\theta _{2}}} &{} &{} Otherwise. \end{array} \right. \end{aligned}$$

(5.10)

Using the quantile function of the marginal distribution in (5.6) , the closed forms for CoVaR risk measures given in (4.5) and (4.8) reduce to

$$\begin{aligned} CoVaR_{\alpha ,\beta ,t}^{L}(Y_{t})=\mu _{t}-\sqrt{2}\sigma _{1,t}\left( \gamma _{inc}^{inv}\left( 1-\frac{\sigma _{1,t}+\sigma _{2,t}}{\sigma _{1,t}} \left( 1+\left( \frac{\alpha \beta }{\tau }\right) ^{-\theta _{1}}-\left( \frac{\alpha }{\tau }\right) ^{-\theta _{1}}\right) ^{-\frac{1}{\theta _{1}} }\right) \right) ^{\frac{1}{\lambda }}, \end{aligned}$$

(5.11)

for $\alpha <\tau$ and

$$\begin{aligned} CoVaR_{\alpha ,\beta }^{U}(Y_{t})=\mu _{t}+\sqrt{2}\sigma _{2,t}\left( \gamma _{inc}^{inv}\left( \frac{\sigma _{1,t}+\sigma _{2,t}}{\sigma _{2,t}} \left( \left[ 1+\left( \frac{(1-\alpha )\beta }{1-\tau }\right) ^{^{^{-\theta _{2}}}}-\left( \frac{1-\alpha }{1-\tau }\right) ^{^{^{-\theta _{2}}}}\right] ^{-\frac{1}{\theta _{2}}}-\frac{\sigma _{1,t}}{\sigma _{1,t}+\sigma _{2,t}}\right) \right) \right) ^{\frac{1}{\lambda }}. \end{aligned}$$

(5.12)

for $\alpha >\tau$.

Application

We implement our approach to assess the markets stock returns’ behavior when the US stock market is in extreme bad and good states (bear market vs. bull market). Since the maximum likelihood estimation method is challenging to implement because of a large number of unknown parameters and the complexity of the model, we adopt the inference functions for margins approach (IFM), also known as the two-step maximum likelihood estimation approach. This approach of estimation has been introduced by Shih and Louis (1995) and Joe and Xu (1996) where the margins’ parameters are estimated first, then the dependence parameters are estimated in the second step. Patton (2006) has proven that this two-step estimation yields asymptotically efficient estimators and normally distributed parameter estimates.

We initialize the estimation using 10% of the observations and utilized an expanding window by adding an extra observation at a time to reestimate the model parameters and compute the quantiles for next period forecasts.

We consider the market daily prices of Brazil, Canada, China, Germany, India, Japan, Russia, UK, and US for the period from April 2005 to June 2020, a sample of 3973 observations. The price indices data are collected from Datastream database while the exports, consumer sentiment index, and exchange rates data are collected from St. Louis fred data.² We compute the continuously compounded returns from the downloaded price series. In Table 2, we report the mean, maximum, minimum, standard deviation, skewness, and kurtosis. We notice that the sample means are all positive except for Brazil, Russia, and UK. The distributions of returns exhibit high kurtosis as an indicator of the presence of extreme returns. The skewness is negative, attesting for a higher likelihood of a loss than a gain of the same amount. The normality and symmetry of the distributions are rejected. This is in line with what is generally acknowledged in the literature (Fama 1965 and Eling 2008).

Table 2 Descriptive statistics for each market’s index

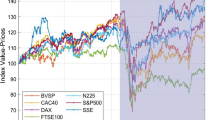
Figures 1 and 8 display the variations in returns. The movements of returns are relatively slow when the markets are in good condition. Otherwise, they move faster in the presence of bad conditions due to the arrival of bad news to the market. In this figure, we observe that returns are more volatile in crisis periods. The clustering of high returns and low returns reveals that the volatility is time-varying and persistent.

Fig. 1

Index’ returns where the shaded areas represent the periods of economic recessions and financial crises

Table 3 reports maximum likelihood parameter estimates for the marginal conditional distributions. Each of the table’s columns gives results for the full sample period estimation for each country. Rows three and four give the estimates of the coefficient of the autoregressive part ($\phi$) and the moving average part ($\varphi$) for the conditional mode (Eq. (5.7)). In the case of Canada, Germany, Russia, the UK, and the US, the conditional mode is high when the past return is high ($\phi >0$ and statistically significant). It seems that past returns have no effect on the conditional mode for the case of Brazil, China, India, and Japan.

Table 3 Marginal models estimation using the maximum likelihood method where *, **, and *** indicate significance at the 0.10, 0.05, and 0.01 levels, respectively

When bad news arrives, the conditional mode increases in the case of Canada, Germany, Japan, Russia, the UK, and the US ($\varphi <0$ and statistically significant) while it is non-significant in the case of Brazil, China, and India. Regarding the volatility regimes, we observe that the volatility is persistent in the bad and good regimes of the financial markets. Both $\beta _{1}$ and $\beta _{2}$ are higher than 0.79, showing that today’s volatility is strongly dependent on past volatility. The leverage effect is statistically significant for both regimes ($\delta _{1}$ and $\delta _{2}$ are statistically significant and positive) except for Canada, where it is negative. In the case of China and Russia, there is no leverage effect in the good regime ($\delta _{2}$ is not statistically significant). This means that in most countries, bad news has a higher effect on volatility than good news. This effect is even more substantial in the bad state of the market ($\delta _{1}>\delta _{2}$). The shape parameter ${\lambda }$ is smaller than two for all countries, revealing that the returns’ distributions have fat tails.³

The independence from the US market is firmly rejected for all countries when the US market is in bad ($\theta _{1}$ is statistically different from zero as stated in Table 4).⁴ However, only Canada and UK depend on the US market when the US market is in a good state, and this effect is small.

Table 4 Copula estimation using the IFM approach where *, **, and *** indicate significance at the 0.10, 0.05, and 0.01 levels, respectively

To capture the effect of the US market on the other countries’ markets in the bad and good extreme states, we compute the ratios $R_{\alpha ,\beta }^{L}$ and $R_{\alpha ,\beta }^{U}$ where the values of $\alpha$ and $\beta$ are set to be 1%. We also consider the cases $\alpha =\beta = 5\%$ and $\alpha =\beta = 10\%$. In this section, we limit our analysis to the case $\alpha =\beta = 1\%$ and the results for the other values of confidence level are given in the Appendix. Table 5 presents the results for $R_{\alpha ,\beta }^{L}$ and $R_{\alpha ,\beta }^{U}$. The table shows that, conditional on the US market being extremely bear or bull, the potential expected systematic extreme loss percentage change and the potential expected systematic extreme gain for all countries are not equal. This suggests that there is an asymmetric spillover effect conditional on the state of the US financial market. The effect is also different across countries. For all countries except Japan, the extreme systematic loss is much higher than the systematic extreme gain. We notice the opposite in the case of Japan. The case of Japan exhibits different behavior. The Japanese financial market sees its potential expected extreme loss decreasing by 29.43% when the US market is in its extreme bad state and its potential expected extreme gain increasing by 7.03% when the US market is in its extreme good state. The results show that all countries’ markets (except Japan) lose more when the US market is extremely bad, but they also gain more when the US market does extremely well (except China). Alternatively, we find that the Chinese market suffers when the US market does extremely well or extremely poorly. As opposed to the Chinese financial market, the Japanese financial market generates less losses when the US market is in its extreme bad state as its potential expected extreme loss decreases by 29.43% conditional on bear US market and its potential expected extreme gain increases by 7.03% when the US market is in its extreme good state. A better illustration of our results is given in Figs. 2 and 3 which display the historical values of the ratios $R_{\alpha ,\beta }^{L}$ and $R_{\alpha ,\beta }^{U}$ when $\alpha =\beta =1\%$ for each country. This figure shows the asymmetric response for each country and the differences between countries’ responses to good and bad news. It also highlights the impact of the financial crisis on the spillover across countries.

Table 5 The potential expected systematic extreme loss and gain percentage changes $R_{\alpha ,\beta }^{L}$ and $R_{\alpha , \beta }^{U}$ ($\alpha =\beta =1\%$)

Fig. 2

The historical values for the potential expected systematic extreme loss $R_{\alpha ,\beta }^{L}$ with $\alpha =\beta =1\%$

Fig. 3

The historical values for the potential expected systematic extreme gain $R_{\alpha ,\beta }^{U}$ with $\alpha =\beta =1\%$

Now, we focus our analysis on the impact of the financial crisis on the spillover. We observe the same results occur if we consider before the crisis (the financial crisis of 2007–2008),⁵ during the crisis, after the crisis periods and during the Covid-19 pandemic. Table 6 presents the values for the ratios $R_{\alpha ,\beta }^{L}$ and $R_{\alpha ,\beta }^{U}$ for these four periods. We notice that the effect is higher during and after the crisis and during the Covid-19 pandemic periods than before. This is because the US financial crisis rapidly developed and spread into global economic shock, resulting in several European and international banks failures, declines in various stock indexes, and large reductions in the market value of equities and commodities. This causes a de-leveraging of financial institutions since they are pushed to sell assets to pay back obligations that could not be refinanced in frozen credit markets. As a result, the insolvency problem is accelerated and causes a decrease in international trade, as is shown in Table 7. This table reports the averages of the US commercial balance deficit to the total US imports ratio for each country and the US consumer sentiment index over four non-overlapping periods: pre-crisis, crisis, post-crisis, and covid-19.⁶ The ratio is decreasing for all countries in the crisis period and Covid-19 pandemic, but the highest decrease is experienced in the case of China. In the case of Russia, the ratio increased by more than 100% during the Covid-19 compared to before the financial crisis period. This significant increase of the ratio in the case of Russia is due to the currency crisis developed at the end of October 2008, where most of the currencies start depreciating compared with the US dollar. The tragedy of the crisis pushed investors to transfer their wealth into stronger currencies such as the yen and the Swiss franc. This behavior caused a reduction in the degree of competitiveness of Chinese traded goods and services. Table 8 shows that all currencies are appreciated vis a vis the US dollar during the 2008 crisis period.⁷ However, after the crisis period, they are stating their depreciation, while the Chinese yuan remains more or less stable on average.⁸ This negative effect of the exchange rate on the Chinese financial market is exacerbated by the decrease of the US Consumer Sentiment Index as shown in the last column of Table 7. The Covid-19 pandemic does more harm to China. During this period, the extreme change in losses is about ten times higher than during the 2007–2008 crisis when the US market is in its extreme bad state, as column three of Table 6 shows (40.17 versus 4.40). In addition and during the Covid-19 pandemic period, the extreme change in gains is about sixteen times lower than during the 2007–2008 crisis, as column three of Table 6 shows (-65.26 versus 3.95). These very extreme results are in large part due to the recent commercial war between the two countries.

Table 6 The potential expected systematic extreme loss and gain percentage changes $R_{\alpha ,\beta }^{L}$ and $R_{\alpha , \beta }^{U}$ for The three non-overlapping periods: pre-crisis, crisis, and post-crisis ($\alpha =\beta =1\%$)

Comparing these results to the obtained values when $\alpha =\beta =5\%$ and $\alpha =\beta =10\%$ (see Appendix Tables 9,10,11,12) show that our results are robust to the confidence levels for most countries and we can confirm the existence of an asymmetric response to bad and good news across countries. Based on Figs. 2, 3, 4, 5, 6, and 7, we can claim that the impact remains similar regardless which confidence levels are used with the same trend and the same asymmetric behavior across countries with some few exceptions. In general, we observe the following ordering $R_{\alpha _{1} ,\beta _{1} }^{L}< R_{\alpha _{2} ,\beta _{2} }^{L}$ for $\alpha _{1} < \alpha _{2}$ and $\beta _{1} < \beta _{2}$. This ordering is due to the fact that the gap between the conditional distribution and the unconditional distributions get narrower as the confidence levels decrease. A such observation does not apply in the context of the Chinese market for which we notice the opposite (Tables 7 and 8). One can explains this by the fact that conditional on the American market the distribution of returns on the Chinese market becomes heavier. For the upper side of the distribution, the behavior is more irregular and we cannot claim to observe such a ordering for most of the countries.

Table 7 The averages of the US commercial balance deficit to the total US imports ratio for each country and the US consumer sentiment index over four non-overlapping periods: pre-crisis, crisis, post-crisis, and covid-19

Table 8 The averages of the country currency exchange rate per one US dollar over four non-overlapping periods: pre-crisis, crisis, post-crisis, and covid-19

To test whether there is a difference between the Potential Expected Systematic Extreme Loss and the Potential Expected Systematic Extreme Gain ($difference=CoVar_{\alpha ,\beta }^{L}-CoVar_{\alpha ,\beta }^{L}$), we conducted three equality tests: the t-test for equality of the means, the Wilcoxon/Mann–Whitney test for equality of medians and the F-test for equality of variances. As shown in Tables 16, 17, and 18, all the tests strongly reject the null hypothesis for all countries as the P-values are below any conventional significance level. This result is enforced by the kernel non-parametric densities estimation (Fig. 8) of the difference between Potential Expected Systematic Extreme Loss and the Potential Expected Systematic Extreme Gain. If there is no difference between the Potential Expected Systematic Extreme Loss and the Potential Expected Systematic Extreme Gain, the density should be degenerate and the graph must put all the mass at zero. On the contrary, the graph shows that the density is not degenerate and put most of the mass away from zero for all countries.

Discussion of results

Our results suggest that an extreme negative shock to the US causes investors to become cash-seeking, inducing them to sell stocks in other countries and causing a contagion effect. The simultaneous intense selling of stocks generates a considerable decrease in the asset prices of other countries. Kyle and Xiong (2001) state that ‘When convergence traders⁹ suffer trading losses, and they have a reduced capacity for bearing risks. This motivates them to liquidate positions in both markets, resulting in reduced market liquidity, increased price volatility in both markets, and increased correlation. Through this mechanism, the wealth effect leads to contagion.’ Yuan (2005) built a model of contagion and found similar results. Based on copula mixture models for dependence, Rodriguez (2007) found that the dependence of the extreme returns is low for the low variance regime and high for the high variance regime. The author concluded that both lower and upper tail dependence increases in the crisis period. Our results in Table 5 are consistent with his results since we find that, conditional on the state of the US market, the potential expected systematic extreme loss percentage change and the potential expected systematic extreme gain percentage change are both higher during the crisis period. However, we find that they remain high in the pre-crisis period, testing for the persistence of the contagion effect. In addition, we find that the presumption of the fact that the contagion effect is stronger for extreme negative returns than for extreme positive returns is in accordance with our results, as shown in Table 5, and this finding becomes stronger, given the results in Table 6. Bae et al. (2003) find similar results.

The increasing economic integration and globalization limited the upside gains because it is unlikely that all the countries have the same ability to outperform at the same time when economic conditions are good. On the other side, the economic integration does not limit the downside risk due to decreasing potential to diversify and hedge the risk in bad times due to the strong connection between international markets. Therefore, global markets fall a lot further together in the bad state than they rise together in the good state. Another explanation for asymmetric spillover is that investors exhibit strong home bias in their preferences and overweigh domestic securities in crisis periods rather than diversify their portfolios across international markets due to increasing asymmetric information, see Coeurdacier and Rey (2013), Chan et al. (2005), and Coval and Moskowitz (1999). Ardalan (2019) surveyed the literature attempting to explain the home bias puzzle. The home bias is also the result of asymmetric expectations leading to overconfidence in local firms Kilka and Weber (2000). This lack of international diversification causes the rise of the level of risk and reduces stock prices heavily in foreign markets implying a significant increase of extreme losses in these markets.

The effect of the co-movements in international stock markets is explained by the differences in the inter-connections between the US stock market and the other global markets. For example, the openness of international trade, the accessibility to each stock market, and also to the policies of each monetary and financial authority lead to the differences between different financial markets. The disparity in response to the good and the bad news in the US market is specific to each market and reflects the nature of the connection between this market and the US market. In the case of China, the explanation of our findings cannot be done without relating the behavior of the stock markets to the macro-economic situation for the American and Chinese economies. The macro-economic factors such as short-term interest rates, the openness of the capital account, and the variability of foreign exchange rates are behind the behavior of the Chinese market given a US bull. The trade war is also a significant factor and affected the performance of the Chinese stock market. In 2018, the American administration started imposing tariffs on Chinese imported goods and announced tariffs on solar panels and washing machines, hundreds of agricultural goods, and high-tech industries. Wang et al. (2021) studied Chinese firms’ stock market reactions to the US–China trade war. Using stock market returns of listed firms, they found a negative effect of the trade war. They also found that the impact is strong when it comes to firms exposed directly to tariff increases.

Conclusion

This paper considers the problem of assessing systematic risks in financial markets. Using a split-type copula to capture dependence between risks and CoVaR risk measures to evaluate the co-movements in the tails, we derive potential expected systematic extreme loss and gain percentages. These percentages show how countries would respond to the extreme movements in the US market. Based on the Clayton-Split copula family, closed-form expressions for these measures are derived. Our empirical application reveals that the contagion effect is different depending on whether the US financial market is in its extreme bad state or extreme good state. The contagion effect is more pronounced in the extreme bad state. The results also show that markets’ response to the systematic risk is different for each country. Such a fact is consistent with the particularity of each market, and a fruitful avenue for future research will be to explain these differences in behavior using a panel macro-economic model. Another extension of our work would be to investigate the extreme systematic loss or gain for individual assets in a given market. The framework and the results presented in this paper measure the impact of systematic spillover between different international markets but does not identify the factors driving the differences between countries’ responses to such a spillover. It is also important to study the extreme co-movements using daily data or even intra-day data where the returns are subject to more volatility and skewness. Another interesting point that the current paper does not cover and could be a very interesting research topic is how the spillover spreads within each market. Addressing these questions would increase our understanding on how financial markets are linked both in good and bad times.

The results obtained in this paper are very informative for policy making. For instance, one can use our framework to study the systematic extreme co-movements and their implications on the macro-economic policy as well as on the micro level for portfolio managers. At macro-economic level, a policy maker can use our framework to identify dependencies between markets in the extremes. It is also possible to measure and quantify the impact of an extreme loss or a gain in a given market on another market. For a portfolio manager, the framework could be useful to identify both potential gains and losses linked to the existence of systematic risks. The measures used in this paper could be applied to test the ability of portfolios to profit from potential systematic gains and minimize systematic losses.

Appendix

Proof of Theorem 1

${\mathbf {C}}_{\mathbf {SC}}(0,v\mathbf {\shortmid }\theta _{1},\theta _{2})$ is a bivariate copula. That is

• Ground function:

Since ${\mathbf {C}}_{1}(u,v\mathbf {\shortmid }\theta _{1})$ and ${\mathbf {C}} _{2}(u,v\mathbf {\shortmid }\theta _{2})$ are copulas then we have ${\mathbf {C}} _{1}(0,u\mathbf {\shortmid }\theta _{1})={\mathbf {C}}_{1}(u,0\mathbf {\shortmid } \theta _{1})={\mathbf {C}}_{2}(0,u\mathbf {\shortmid }\theta _{2})={\mathbf {C}} _{2}(u,0\mathbf {\shortmid }\theta _{2})=0,$ thus

$$\begin{aligned}&{\mathbf {C}}_{\mathbf {SC}}(0,v\mathbf {\shortmid }\theta _{1},\theta _{2})=\tau {\mathbf {C}}_{1}(0,v^{\kappa }\mathbf {\shortmid }\theta _{1})^{\frac{1}{\kappa }}=0 \end{aligned}$$

(9.1)

$$\begin{aligned}&{\mathbf {C}}_{\mathbf {SC}}\left( u,0\shortmid \theta _{1},\theta _{2}\right) =\tau {\mathbf {C}}_{1}\left( \frac{u^{\kappa }}{\tau ^{\kappa }},0\mathbf { \shortmid }\theta _{1}\right) ^{\frac{1}{\kappa }}I_{u\leqslant \tau } \nonumber \\&\quad +\left( 1-\tau \right) {\mathbf {C}}_{2}\left( \left( \frac{u-\tau }{1-\tau } \right) ^{\kappa },0\mathbf {\shortmid }\theta _{2}\right) ^{\frac{1}{\kappa } }(1-I_{u\leqslant \tau }) \nonumber \\= & {} 0. \end{aligned}$$

(9.2)

• Uniform Marginals:

Recall that ${\mathbf {C}}_{1}(1,u\mathbf {\shortmid }\theta _{1})={\mathbf {C}} _{2}(1,u\mathbf {\shortmid }\theta _{2})=u$ and ${\mathbf {C}}_{1}(u,1\mathbf { \shortmid }\theta _{1})={\mathbf {C}}_{2}(u,1\mathbf {\shortmid }\theta _{2})=u$ , thus

$$\begin{aligned} {\mathbf {C}}_{\mathbf {SC}}\left( 1,v\shortmid \theta _{1},\theta _{2}\right)= & {} \tau v+\left( 1-\tau \right) {\mathbf {C}}_{2}\left( \left( \frac{1-\tau }{ 1-\tau }\right) ^{\kappa },v^{\kappa }\mathbf {\shortmid }\theta _{2}\right) ^{\frac{1}{\kappa }} \nonumber \\= & {} \tau v+\left( 1-\tau \right) v \nonumber \\= & {} v. \end{aligned}$$

(9.3)

and

$$\begin{aligned} {\mathbf {C}}_{\mathbf {SC}}\left( u,1\shortmid \theta _{1},\theta _{2}\right)= & {} \tau {\mathbf {C}}_{1}\left( \frac{u^{\kappa }}{\tau ^{\kappa }},1\mathbf {\shortmid }\theta _{1}\right) ^{\frac{1}{\kappa }}I_{u\leqslant \tau } \nonumber \\&+\left[ \tau +\left( 1-\tau \right) {\mathbf {C}}_{2}\left( \left( \frac{ u-\tau }{1-\tau }\right) ^{\kappa },1\mathbf {\shortmid }\theta _{2}\right) ^{ \frac{1}{\kappa }}\right] (1-I_{u\leqslant \tau }) \nonumber \\= & {} uI_{u\leqslant \tau }+\left[ \tau +\left( 1-\tau \right) \left( \frac{ u-\tau }{1-\tau }\right) \right] (1-I_{u\leqslant \tau }) \nonumber \\= & {} uI_{u\leqslant \tau }+u(1-I_{u\leqslant \tau }) \nonumber \\= & {} u. \end{aligned}$$

(9.4)

• 2-non-decreasing:

We have to show that ${\mathbf {C}}_{\mathbf {SC}}(u_{2},v_{2}\shortmid \theta _{1},\theta _{2})-{\mathbf {C}}_{\mathbf {SC}}(u_{2},v_{1}\shortmid \theta _{1},\theta _{2})-{\mathbf {C}}_{\mathbf {SC}}(u_{1},v_{2}\shortmid \theta _{1},\theta _{2})+{\mathbf {C}}_{\mathbf {SC}}(u_{1},v_{1}\shortmid \theta _{1},\theta _{2})\geqslant 0$ for all $0\leqslant u_{1}\leqslant u_{2}\leqslant 1$ and $0\leqslant v_{1}\leqslant v_{2}\leqslant 1$. This is the result of $\frac{\partial ^{2}{\mathbf {c}}_{SC}(u,v,\theta ,\vartheta )}{ \partial u\partial v}\geqslant 0.$

The density is given by

$$\begin{aligned} \mathbf {{\mathbf {c}}_{SC}}\left( u,v\shortmid \theta _{1},\theta _{2}\right) =\left\{ \begin{array}{ccc} \begin{array}{c} \kappa \frac{u^{\kappa -1}}{\tau ^{\kappa -1}}v^{\kappa -1}{\mathbf {C}} _{1}\left( \frac{u^{\kappa }}{\tau ^{\kappa }},v^{\kappa }\mathbf {\shortmid } \theta _{1}\right) ^{\frac{1}{\kappa }-2} \\ \left[ \left( \frac{1}{\kappa }-1\right) {\mathbf {C}}_{1,v^{*}}\left( \frac{u^{\kappa }}{\tau ^{\kappa }},v^{\kappa }\mathbf {\shortmid }\theta _{1}\right) {\mathbf {C}}_{1,u^{**}}\left( \frac{u^{\kappa }}{\tau ^{\kappa }},v^{\kappa }\mathbf {\shortmid }\theta _{1}\right) \right. \\ +\left. {\mathbf {C}}_{1}\left( \frac{u^{\kappa }}{\tau ^{f\left( \tau \right) } },v^{\kappa }\mathbf {\shortmid }\theta _{1}\right) {\mathbf {c}}_{1}\left( \frac{u^{\kappa }}{\tau ^{\kappa }},v^{\kappa }\mathbf {\shortmid }\theta _{1}\right) \right] \end{array} &{} \text {if} &{} u\leqslant \tau \\ &{} &{} \\ \begin{array}{c} \kappa v^{\kappa -1}\left( \frac{u-\tau }{1-\tau }\right) ^{\kappa -1} {\mathbf {C}}_{2}\left( \left( \frac{u-\tau }{1-\tau }\right) ^{\kappa },v^{\kappa }\mathbf {\shortmid }\theta _{2}\right) ^{\frac{1}{\kappa }-2} \\ \left[ \left( \frac{1}{\kappa }-1\right) {\mathbf {C}}_{2,v^{*}}\left( \left( \frac{u-\tau }{1-\tau }\right) ^{\kappa },v^{\kappa }\mathbf { \shortmid }\theta _{2}\right) {\mathbf {C}}_{2,u^{*}}\left( \left( \frac{ u-\tau }{1-\tau }\right) ^{\kappa },v^{\kappa }\mathbf {\shortmid }\theta _{2}\right) \right. \\ +\left. {\mathbf {C}}_{2}\left( \left( \frac{u-\tau }{1-\tau }\right) ^{\kappa },v^{\kappa }\mathbf {\shortmid }\theta _{2}\right) {\mathbf {c}}_{2}\left( \left( \frac{u-\tau }{1-\tau }\right) ^{\kappa },v^{\kappa }\mathbf { \shortmid }\theta _{2}\right) \right] \end{array}&\,&Otherwise \end{array} \right\} . \end{aligned}$$

(9.5)

It is easy to notice that all the components of the density are positive given that $0<\kappa \leqslant 1$, it follows that ${\mathbf {c}} _{SC}(u,v,\theta ,\vartheta )=\frac{\partial ^{2}{\mathbf {c}}_{SC}(u,v,\theta ,\vartheta )}{\partial u\partial v}\geqslant 0$. Thus, ${\mathbf {C}}_{SC}(.)$ is 2-non-decreasing function.

Proof of Proposition 1

In the following proof, we dropped the time index for simplicity. With a slight change of the results of Box and Tiao (1973) and Kotz and Podgorski (2001), we get the CDF and the quantile functions of (5.1) as

$$\begin{aligned} G(x)= & {} \int _{-\infty }^{x}\frac{\lambda }{2\sqrt{2}\Gamma (\frac{1}{\lambda })}\exp \left( -\left| \frac{t}{\sqrt{2}}\right| ^{\lambda }\right) \mathrm{{d}}t \end{aligned}$$

(9.6)

$$\begin{aligned}= & {} \frac{1}{2}\left( 1+\mathrm{{sign}}\left( x\right) \gamma _{inc}\left( \left| \frac{x}{\sqrt{2}}\right| ^{\lambda },\frac{1}{\lambda }\right) \right) , \end{aligned}$$

(9.7)

and

$$\begin{aligned} G^{inv}(x)=\sqrt{2}\mathrm{{sign}}\left( 2u-1\right) \left( \gamma _{inc}^{inv}\left( 2u-1,\frac{1}{\lambda }\right) \right) ^{\frac{1}{\lambda }}. \end{aligned}$$

(9.8)

Here, u is a uniform random variable $\left( i.e.,\text { }u\in \left[ 0,1 \right] \right)$. The functions $\Gamma (x)$ and $\gamma _{inc}\left( x\right)$ are the Gamma function, the Gamma distribution CDF given by

$$\begin{aligned} \Gamma (x)=\int _{0}^{+\infty }t^{x-1}\exp \left[ -t\right] \mathrm{{d}}t, \end{aligned}$$

(9.9)

and

$$\begin{aligned} \gamma _{inc}\left( x\right) =\frac{\int _{0}^{x}t^{x-1}\exp \left[ -t\right] \mathrm{{d}}t}{\Gamma (x)}. \end{aligned}$$

(9.10)

The function $\gamma _{inc}^{inv}$ is the quantile of Gamma distribution.

Let x $\sim$SEP$(\mu ,\sigma _{1},\sigma _{2},\lambda )$ then by (5.2), the CDF is given by

$$\begin{aligned} F(x)=k\left\{ \begin{array}{ccc} I_{1} &{} \text {if} &{} x\leqslant \mu \\ I_{2} &{} &{} \text {Otherwise} \end{array} \right. , \end{aligned}$$

(9.11)

where

$$\begin{aligned} I_{1}=\int _{-\infty }^{x}\frac{\lambda }{2\sqrt{2}\Gamma (\frac{1}{\lambda }) }\exp \left( -\left| \frac{t-\mu }{\sqrt{2}\sigma _{1}}\right| ^{\lambda }\right) \mathrm{{d}}t, \end{aligned}$$

(9.12)

and

$$\begin{aligned} I_{2}= & {} \int _{-\infty }^{\mu }\frac{\lambda }{2\sqrt{2}\Gamma (\frac{1}{ \lambda })}\exp \left( -\left| \frac{t-\mu }{\sqrt{2}\sigma _{1}}\right| ^{\lambda }\right) \mathrm{{d}}t \end{aligned}$$

(9.13)

$$\begin{aligned}&+\int _{\mu }^{x}\frac{\lambda }{2\sqrt{2}\Gamma (\frac{1}{\lambda })}\exp \left( -\left| \frac{t-\mu }{\sqrt{2}\sigma _{2}}\right| ^{\lambda }\right) \mathrm{{d}}t. \end{aligned}$$

(9.14)

Let $h=\frac{t-\mu }{\sigma _{1}}$ then $t=\mu +\sigma _{1}h$ and $\mathrm{{d}}t=\sigma _{1}\mathrm{{d}}h$

$$\begin{aligned} I_{1}= & {} \int _{-\infty }^{x}\frac{\lambda }{2\sqrt{2}\Gamma (\frac{1}{ \lambda })}\exp \left( -\left| \frac{t-\mu }{\sqrt{2}\sigma _{1}}\right| ^{\lambda }\right) \mathrm{{d}}t\nonumber \\= & {} \sigma _{1}\int _{-\infty }^{\frac{x-\mu }{\sigma _{1}}}\frac{\lambda }{2 \sqrt{2}\Gamma (\frac{1}{\lambda })}\exp \left( -\left| \frac{h}{\sqrt{2 }}\right| ^{\lambda }\right) \mathrm{{d}}h. \end{aligned}$$

(9.15)

Using (9.7), we get,

$$\begin{aligned} I_{1}=\sigma _{1}\frac{1}{2}\left( 1+\mathrm{{sign}}\left( x-\mu \right) \gamma _{inc}\left( \left| \frac{x-\mu }{\sqrt{2}\sigma _{1}}\right| ^{\lambda },\frac{1}{\lambda }\right) \right) . \end{aligned}$$

(9.16)

If we let $x=\mu$ in (9.12), we get

$$\begin{aligned} \int _{-\infty }^{\mu }\frac{\lambda }{2\sqrt{2}\Gamma (\frac{1}{\lambda })} \exp \left( -\left| \frac{t-\mu }{\sqrt{2}\sigma _{1}}\right| ^{\lambda }\right) \mathrm{{d}}t= & {} \frac{\sigma _{1}}{2}\left( 1+\mathrm{{sign}}\left( x-\mu \right) \gamma _{inc}\left( 0,\frac{1}{\lambda }\right) \right) \end{aligned}$$

(9.17)

$$\begin{aligned}= & {} \frac{\sigma _{1}}{2}. \end{aligned}$$

(9.18)

Thus

$$\begin{aligned} I_{2}= & {} \frac{\sigma _{1}}{2}+\int _{\mu }^{x}\frac{\lambda }{2\sqrt{2} \Gamma (\frac{1}{\lambda })}\exp \left( -\left| \frac{t-\mu }{\sqrt{2} \sigma _{2}}\right| ^{\lambda }\right) \mathrm{{d}}t \nonumber \\= & {} \frac{\sigma _{1}}{2}+\int _{-\infty }^{x}\frac{\lambda }{2\sqrt{2}\Gamma ( \frac{1}{\lambda })}\exp \left( -\left| \frac{t-\mu }{\sqrt{2}\sigma _{2}}\right| ^{\lambda }\right) \mathrm{{d}}t \nonumber \\&-\int _{-\infty }^{\mu }\frac{\lambda }{2\sqrt{2}\Gamma (\frac{1}{\lambda }) }\exp \left( -\left| \frac{t-\mu }{\sqrt{2}\sigma _{2}}\right| ^{\lambda }\right) \mathrm{{d}}t. \end{aligned}$$

(9.19)

By using similar results as in (9.16) and (9.18), we get

$$\begin{aligned} I_{2}= & {} \frac{\sigma _{1}}{2}-\frac{\sigma _{2}}{2}+\frac{\sigma _{2}}{2} \left( 1+\mathrm{{sign}}\left( x-\mu \right) \gamma _{inc}\left( \left| \frac{ x-\mu }{\sqrt{2}\sigma _{2}}\right| ^{\lambda },\frac{1}{\lambda } \right) \right) \nonumber \\= & {} \frac{\sigma _{1}}{2}+\frac{\sigma _{2}}{2}\mathrm{{sign}}\left( x-\mu \right) \gamma _{inc}\left( \left| \frac{x-\mu }{\sqrt{2}\sigma _{2}}\right| ^{\lambda },\frac{1}{\lambda }\right) . \end{aligned}$$

(9.20)

Thus

$$\begin{aligned} F(x)=k\left\{ \begin{array}{ccc} \frac{\sigma _{1}}{2}\left( 1-\gamma _{inc}\left( \left| \frac{x-\mu }{ \sqrt{2}\sigma _{1}}\right| ^{\lambda },\frac{1}{\lambda }\right) \right) &{} if &{} x<\mu \\ \frac{\sigma _{1}}{2}+\frac{\sigma _{2}}{2}\gamma _{inc}\left( \left| \frac{x-\mu }{\sqrt{2}\sigma _{2}}\right| ^{\lambda },\frac{1}{\lambda } \right) &{} &{} Otherwise \end{array} \right. . \end{aligned}$$

(9.21)

Pushing x to plus infinity in (9.18), we get

$$\begin{aligned} F(+\infty )=k\left( \frac{\sigma _{1}}{2}+\frac{\sigma _{2}}{2}\right) =1. \end{aligned}$$

(9.22)

Therefore, we have

$$\begin{aligned} k=\frac{2}{\sigma _{1}+\sigma _{2}}, \end{aligned}$$

(9.23)

and

$$\begin{aligned} F(x)=\left\{ \begin{array}{ccc} \frac{\sigma _{1}}{\sigma _{1}+\sigma _{2}}\left( 1-\gamma _{inc}\left( \left| \frac{x-\mu }{\sqrt{2}\sigma _{1}}\right| ^{\lambda },\frac{ 1}{\lambda }\right) \right) &{} if &{} x<\mu \\ \frac{\sigma _{1}}{\sigma _{1}+\sigma _{2}}+\frac{\sigma _{2}}{\sigma _{1}+\sigma _{2}}\gamma _{inc}\left( \left| \frac{x-\mu }{\sqrt{2} \sigma _{2}}\right| ^{\lambda },\frac{1}{\lambda }\right) &{} &{} Otherwise \end{array} \right. . \end{aligned}$$

(9.24)

Quantile q of level p is given by

$$\begin{aligned} p= & {} \left\{ \begin{array}{ccc} \frac{\sigma _{1}}{\sigma _{1}+\sigma _{2}}\left( 1-\gamma _{inc}\left( \left| \frac{q-\mu }{\sqrt{2}\sigma _{1}}\right| ^{\lambda },\frac{1 }{\lambda }\right) \right) &{} if &{} q<\mu \\ \frac{\sigma _{1}}{\sigma _{1}+\sigma _{2}}+\frac{\sigma _{2}}{\sigma _{1}+\sigma _{2}}\gamma _{inc}\left( \left| \frac{q-\mu }{\sqrt{2}\sigma _{2}}\right| ^{\lambda },\frac{1}{\lambda }\right) &{} &{} Otherwise \end{array} \right. \end{aligned}$$

(9.25)

$$\begin{aligned} q= & {} \left\{ \begin{array}{ccc} \mu -\sqrt{2}\sigma _{1}\left( \gamma _{inc}^{inv}\left( 1-\frac{\sigma _{1}+\sigma _{2}}{\sigma _{1}}p\right) \right) ^{\frac{1}{\lambda }} &{} if &{} p<\frac{\sigma _{1}}{\sigma _{1}+\sigma _{2}} \\ \mu +\sqrt{2}\sigma _{2}\left( \gamma _{inc}^{inv}\left( \frac{\sigma _{1}+\sigma _{2}}{\sigma _{1}}p-1\right) \right) ^{\frac{1}{\lambda }} &{} &{} Otherwise \end{array} \right. . \end{aligned}$$

(9.26)

Results for $\alpha =5\%$ and $\beta =5\%$

Tables (9, 10, and Figs. 4 and 5)

Table 9 The potential expected systematic extreme loss and gain percentage changes $R_{\alpha ,\beta }^{L}$ and $R_{\alpha , \beta }^{U}$ ($\alpha =\beta =5\%$)

Table 10 The potential expected systematic extreme loss and gain percentage changes $R_{\alpha ,\beta }^{L}$ and $R_{\alpha , \beta }^{U}$ for The four non-overlapping periods: pre-crisis, crisis, and post-crisis ($\alpha =\beta =5\%$)

Fig. 4

The historical values for the potential expected systematic extreme loss $R_{\alpha ,\beta }^{L}$ with $\alpha =\beta =5\%$

Fig. 5

The historical values for the potential expected systematic extreme gain $R_{\alpha ,\beta }^{U}$ with $\alpha =\beta =5\%$

Results for $\alpha =10\%$ and $\beta =10\%$

Tables 11, 12 and Figs. 6,7.

Table 11 The potential expected systematic extreme loss and gain percentage changes $R_{\alpha ,\beta }^{L}$ and $R_{\alpha , \beta }^{U}$ ($\alpha =\beta =10\%$)

Table 12 The potential expected systematic extreme loss and gain percentage changes $R_{\alpha ,\beta }^{L}$ and $R_{\alpha , \beta }^{U}$ for The four non-overlapping periods: pre-crisis, crisis, and post-crisis ($\alpha =\beta =10\%$)

Fig. 6

The historical values for the potential expected systematic extreme loss $R_{\alpha ,\beta }^{L}$ with $\alpha =\beta =10\%$

Fig. 7

The historical values for the potential expected systematic extreme gain $R_{\alpha ,\beta }^{U}$ with $\alpha =\beta =10\%$

Tests of conditional location and scale parameter models

Tables 13, 14 and 15

Table 13 Schwartz Criterion for conditional location and scale parameter models

Table 14 Akaike Criterion for conditional location and scale parameter models

Table 15 Hannan–Quinn Criterion conditional location and scale parameter models

Difference between $CoVar_{\alpha ,\beta }^{L}$ and $CoVar_{\alpha ,\beta }^{U}$

Tables 16, 17, 18 and Fig. 8

Table 16 Tests of difference between Potential Expected Systematic Extreme Loss and the Potential Expected Systematic Extreme Gain (Coverage rate of 1%)

Table 17 Tests of difference between Potential Expected Systematic Extreme Loss and the Potential Expected Systematic Extreme Gain (Coverage rate of 5%)

Table 18 Tests of difference between Potential Expected Systematic Extreme Loss and the Potential Expected Systematic Extreme Gain (Coverage rate of 10%)

Fig. 8

The kernel non-parametric densities estimation of the difference between Potential Expected Systematic Extreme Loss and the Potential Expected Systematic Extreme Gain