Abstract
After-sales services have become high-margin businesses that account for larger portions of corporate profits. Delivering the after-sales services is challenging as after-sales services supply chains are significantly different than production–distribution supply chains. The literature provides little guidance on the use of quantitative methods for after-sales services network design. We present a mixed integer linear programming problem formulation to determine warehouse locations, assign repair vendors to facilities and choose mode of transportation while minimizing the total network cost. We transform the large-scale real-life problem of a household appliances manufacturer into a smaller scale to solve optimally in reasonable time. Through a scenario-based approach, we evaluate different configurations of a decentralized network with choices of transportation mode. We test the sensitivity of the solutions. The total cost decreases with additional choices of transportation mode and only slightly increases with the next-day delivery policy while the network solution may change significantly.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
More and more manufacturing companies started recognizing their after-sales activities as a significant foundation of revenue, profit and competitive advantage (Saccani et al, 2007; Cohen et al, 2006). The profit margins for after-sales services are 30% while that of the initial sales are around 10% (Murthy et al, 2004). In this respect, the after-sales services are not only high-margin businesses but also they account for larger portions of corporate profits, represent the longest-lasting revenue stream and require the smallest investment (Cohen et al, 2006).
Despite the various benefits that can be attained by focusing on the after-sales services, delivering after-sales services is challenging as the after-sales services supply chains are significantly different than the production–distribution supply chains (Cohen et al, 2006). Designing the right after-sales services supply chain strategy with a centralized approach involves service targets on cost reduction and efficiency while a distributed approach anticipates varying requirements in terms of urgency (or criticality) of the customers and involves availability and rapid response as service targets (Cohen et al, 2000). In an empirical analysis of 48 Italian firms, timeliness of after-sales services has received high emphasis for 42% of the companies in automotive industry and only 33% of companies producing household appliances and information technologies (IT) and consumer electronics (Saccani et al, 2006). Even within the same industry such as the computer industry in North America, some customers request same-day on-site service for a premium payment while others are satisfied even if the time required to provide the service exceeds three days (Cohen et al, 2000).
In the literature, few papers deal with configuration of after-sales services supply chains (Saccani et al, 2007), and even fewer ones make use of quantitative tools. We work with a major household appliances manufacturer in Turkey to improve their centralized after-sales services supply chain that consists of suppliers, distribution centers, warehouses and repair vendors. The company wants to determine optimum number of facilities to operate, capacities of the facilities, hierarchical structure of the network of facilities, relationships among facilities and selection of transportation mode so as to decrease the logistics costs of delivery of the spare parts to the repair vendors.
In order to optimize the spare parts delivery network, we define a static single-period multi-commodity multi-level network design problem and develop a mixed integer linear mathematical programming formulation to solve this problem while minimizing the total network cost. In addition to facility location decisions associated with the distribution center and warehouses, we are also concerned with associating repair vendors with facilities and transportation mode selection.
Our contribution can be summarized as follows:
-
We develop a mathematical model for the after-sales services network design problem which also considers the selection of transportation mode.
-
We work with an extremely large data set that contains more than 44000 stock keeping units (SKUs) transshipped over a network of almost 700 facility locations, and we solve the network design problem optimally after transforming this data set into a smaller scale.
-
We present alternative scenarios to reflect a variety of network design schemes along with new facility locations and alternative transportation modes, and find the optimal network design for each scenario. We test the sensitivity of the solutions to an increased responsiveness enforced by a next-day delivery policy.
Overall, this is the first study presenting a quantitative tool for configuration of after-sales logistics networks and demonstrating the results with real-life data.
After the literature review in Section 2, Section 3 follows with the analysis of the existing system. We discuss the problem definition in detail in Section 4 and present the mathematical programming formulation for the network design problem in Section 5. Section 6 provides the details of transforming the data into a smaller scale followed by the computational analysis in Section 7 where we present and compare the results of the scenarios. Finally, conclusions and directions for future research are given in Section 8.
2 Literature review
After-sales service logistics systems facilitate providing service parts, maintenance and repair services to users of the products (Cohen et al, 1997). Over the years, the after-sales services have also embraced the reverse flows, handling end-of-life returns as well as return, repair and disposal of failed components (Cohen et al, 2006). A number of studies that design network logistics for such post-sales services have emerged (Amini et al, 2005; Du and Evans, 2008; Eskandarpour et al, 2013, 2014).
Even when the reverse flows are excluded, the design and management of after-sales service logistics are complex and significantly different than that of product distribution systems due to the following factors:
-
the high number and variety of parts involved (Cohen et al, 2006);
-
the provision of multiple classes of service (Cohen et al, 1999);
-
high responsiveness requirement (Murthy et al, 2004) to maximize product availability (uptime) (Cohen et al, 2006);
-
unpredictable (sporadic) demand (Huiskonen, 2001; Cohen et al, 2006);
-
lumpy or intermittent nature of demand (Boylan and Syntetos, 2010);
-
the geographical spread of the installed products (Cohen et al, 1999);
-
obsolescence risk of inventory (Cohen et al, 2006);
-
the prices of individual parts may be high (Huiskonen, 2001); and
-
the use of a single delivery network that is capable of distributing a heterogeneous product portfolio (Cohen et al, 2006).
Control characteristics of spare parts such as criticality, specificity, demand pattern and value of parts prominently affect the design of after-sales logistics systems in terms of network structure, positioning of material, responsibility of control and control principles (Huiskonen, 2001). Due to the effect of such control characteristics, there is no one-size-fits-all option for designing after-sales logistics systems. The research on configuration of after-sales supply chain includes a literature review on product warranty logistics (Murthy et al, 2004), an analysis of gap between research and industry on spare parts classification and demand forecasting for stock control (Bacchetti and Saccani, 2012) and a benchmark analysis for technologically complex high value products (Cohen et al, 1997). There are also studies using empirical analysis on companies producing durable goods (Saccani et al, 2007) and also in industries such as automotive, household appliances, IT and consumer electronics (Saccani et al, 2006). Other studies present design of after-sales service logistics for specific companies such as IBM (Cohen et al, 1990); Teradyne in manufacturing electronic testing equipment used in semiconductor and electronics (Cohen et al, 1999); Saturn in conducting authorized automobile repairs (Cohen et al, 2000); a heavy equipment manufacturer (Persson and Saccani, 2009); a manufacturer of digital cinema projectors (Landrieux and Vandaele, 2012); and a manufacturer of high value capital assets (Driessen et al, 2015).
Dennis and Kambil (2003) expect that after-sales services supply chains are to be more complicated due to complex logistical and information flows. Hertz et al (2012) examine the applicability of existing supply chain planning methods to service network planning and present how the traditional manufacturing supply chain and the service network differ from each other with respect to issues taken into consideration at the network configuration phase. They claim that planning problems tackled in traditional supply chains decades ago are becoming central issues for service networks such as after-sales services networks.
Among the limited research published on the configuration of after-sales logistics networks, quantitative methods that involve the determination of facility locations and flows among them are proposed in Persson and Saccani (2009), Jalil et al (2011), Wu et al (2011) and Landrieux and Vandaele (2012). Persson and Saccani (2009) utilize simulation over different demand scenarios to calculate transportation costs in order to determine the allocation of suppliers and parts for a new second warehouse. Jalil et al (2011) consider a spare parts logistics network for IBM; they determine the flow rate and stock levels at intermediate stock locations while time-based service levels are also imposed as constraints in the problem formulation. Their main focus is to identify the usability of collected installed base information and analyze the effects of data quality. Landrieux and Vandaele (2012), given service-level agreements for 4, 6 and 8 h for only one randomly selected spare part, provide solutions for both the facility location problem and the spare parts inventory management. Wu et al (2011) discuss a comprehensive approach that integrates the network design and transportation mode selection along with the vendor selection decisions for the configuration of logistics services. They provide a mathematical formulation of the problem, and their proposed solution approaches include metaheuristics. A comparison of the features of these studies with our study is presented in Table 1.
3 Existing system analysis
Our problem belongs to a household appliances manufacturer in Turkey. The company engages in the production, marketing and sales, and after-sales services of products such as consumer electronics, small home appliances, refrigerators, freezers, washing machines and dishwashers. The company offers products and services around the world with its 24000 employees, has 14 different production plants in five countries and executes its sales and marketing companies all over the world with its 10 brands. In Turkey, around 15 million households use the company’s products.
Due to company’s customer satisfaction policies, responding to customers in a predetermined 3-day time-windows is critical. The company aims to further shorten this response time while decreasing after-sales costs. As of 2013, the company’s spare part distribution network contains 44408 different SKUs. Overseas countries and 531 domestic repair vendors require these parts, which are procured from 83 domestic suppliers, company-owned production plants and imports. Warehouses are located at 8 different places in Turkey. Repair vendors keep stocks for an anticipated demand level. In case of stockout, they request spare parts from the facility they are assigned to; it may be a warehouse or a distribution center depending on the location of the repair vendor. A total of 135 repair vendors that are very close to the distribution center in Istanbul are not assigned to a warehouse as the distribution center provides the spare parts directly to these repair vendors. Moreover, the distribution center is responsible for the import and export activities of the after-sales services spare parts distribution system.
3.1 Suppliers and spare parts
In the after-sales service system, there are three types of sources for the procurement of spare parts: internal suppliers, external suppliers and import from overseas countries. Internal suppliers are production plants of the company. Each internal supplier produces only one product type including its spare parts. They provide 62% of the spare parts in volume. In addition to these internal suppliers, there are 83 external suppliers and one supplier for import activities, which provide the 34 and 4% of the spare parts volume, respectively. External suppliers are local manufacturers which also provide spare parts to the after-sales services of the company. In total, 93 different suppliers provide the network with spare parts. Each spare part has a unique supplier (i.e. a spare part cannot be procured from more than one supplier).
In the existing highly centralized system, each supplier sends the spare parts to the distribution center. Transportation costs from external suppliers and import location to the distribution center have no cost on the company as they are paid by these suppliers. But the company has to pay transportation costs for transportation starting from the internal suppliers to the distribution center, and all the way down to the repair vendors.
3.2 Distribution centers and warehouses
After-sales service system includes three distribution centers located very close to each other: 27 km in-between. As each distribution center keeps stock of different spare parts, a single SKU cannot be stored in two different distribution centers. Therefore, these three distribution centers can be treated as a single representative distribution facility.
Along with the representative distribution center, there are currently 8 warehouses located in major cities such as Ankara, Adana, Antalya, Bursa. Each warehouse represents a spatial region, and all repair vendors in that region can only be served by that particular designated warehouse except those repair vendors in close proximity to the distribution center in Istanbul. They are directly served by the distribution center and considered in two separate regions as Istanbul-1 and Istanbul-2. Overall, repair vendors are divided into 10 regions while the number of repair vendors in a region ranges from 27 to 72. The distribution center transfers spare parts to warehouses and directly to repair vendors in close proximity. The warehouses and repair vendors ship the ordered spare parts twice a week. Therefore, each warehouse is served once every three days and on the same days of each week.
3.3 Repair vendors
As of 2013, there are 531 active repair vendors in the after-sales services spare parts distribution system. Repair vendors are divided into two categories: inner city and suburban. Delivery strategies are based on the repair vendor’s category. A total of 171 repair vendors out of 531 are inner-city repair vendors. All deliveries are carried out with routes that are predetermined by the company. For suburban repair vendors, predetermined delivery routes are fixed. However, some inner-city routes may change depending on the demand from the repair vendors. For each route, deliveries are carried out twice a week (i.e. there are 3 days between subsequent deliveries to the same location).
4 Problem definition
To provide a setting for the existing system and to model the corresponding after-sales network, we consider the single-period, multi-commodity, multi-level location problem with deterministic demand. We assume a static model and optimize the design of the after-sales network considering one representative period. Considering the representative period (i.e. half-week) data, although there are fluctuations in demand of the spare parts within a year, other parameters such as costs and capacities do not vary over time. As variations in demand and other parameters are not predictable, incorporating time dimension to accommodate future adjustments in facility decisions as well as related assignment decisions is not feasible. We also assume the demand for spare parts is inelastic and, hence, independent of spatial decisions on the locations of distribution centers and warehouses. There is single-sourcing restriction for each spare part, and the suppliers are assumed to have sufficient capacity to meet the demand of all repair vendors during the planning horizon. Similarly, single-sourcing constraints are valid for each repair vendor requiring them to be served by one facility. The transportation costs are assumed to be linear functions of the volumetric weight and distance. The distribution centers and the warehouses have known capacities. There are no restrictions on the number of distribution centers and warehouses that can be operated. Transfers of spare parts between warehouses are not allowed. Although there are some other restrictions on the transportation links in the existing system, they are not imposed during modeling. Such transportation link restrictions will be introduced using a scenario-based approach, and their effects will be analyzed in our computational analysis. The determination of inventory levels of the spare parts is beyond the scope of our study, since they are tactical decisions and the strategic decisions in our after-sales network design problem do not incorporate capacity planning.
Given the existing system, along with locations of alternative new region warehouses, the decisions of the after-sales network design problem so as to minimize total cost include the following:
-
number of distribution centers and warehouses,
-
location of the new facilities if necessary along with the closing down the existing facilities,
-
assignment of the suppliers to facilities,
-
assignment of repair vendors to facilities and
-
choice of transportation mode between repair vendors and facilities.
In order to solve this problem for a variety of network configurations, we use a scenario-based approach.
5 Mathematical formulation
We develop a mathematical programming problem formulation of the after-sales services network design problem. The formulation corresponds to a single objective mixed integer linear programming formulation of a multi-level facility location problem (Şahin and Süral, 2007). We define the notation in Table 2 where D is the set of distribution centers, W is the set of warehouses, S is the set of suppliers, R is the set of repair vendors, I is the set of spare parts, and M is the set of transportation modes. As each supplier is providing a single spare part, A i denotes the supplier that is producing spare part i.
We use the following decision variables:
- \( Q_{sd} \) :
-
Amount of product shipped from supplier s to distribution center d
- \( Q_{sw} \) :
-
Amount of product shipped from supplier s to warehouse w
- \( Q_{dw}^{i} \) :
-
Amount of product i shipped from distribution center d to warehouse w
- \( Q_{drm}^{i} \) :
-
Amount of product i shipped from distribution center d to repair vendor r by transportation mode m
- \( Q_{wrm}^{i} \) :
-
Amount of product i shipped from warehouse w to repair vendor r by transportation mode m
The resulting mathematical formulation is as follows:
The objective function (1) minimizes the total cost consisting of the fixed costs associated with opening and operating the facilities as well the transportation costs between the facilities. Constraint (2) is the inbound–outbound balance equations for each distribution center that ensures the conservation of flow of each spare part. Constraint (3) ensures the conservation of flow for each warehouse and spare part. Constraint (4) consists of the upper bound constraints honoring inbound handling capacity of each distribution center. The same inbound handling constraint for warehouses is given by the constraint (5). These constraints also link the facility opening decisions with flow feasibility: if the facility is open, an upper bound for inbound handling capacity is active. Constraint (6) ensures that the demand of a repair vendor is satisfied by a distribution center, if the repair vendor is assigned to a distribution center, and the total delivered quantity to the repair vendor should be equal to the total demand of repair vendor. Furthermore, constraint (7) ensures the same if the demand of repair vendor is met from a warehouse. Constraint (8) is the single-sourcing constraint ensuring that a repair vendor’s demand can be fulfilled by either a warehouse or a distribution center and only by a single transportation mode type. Supply capacity is represented with constraint (9) where for each item total procurement equals available supply. Constraint (10) and constraint (11) are the domain constraints for the decision variables.
(1)–(11) provides a generic mixed integer linear programming problem formulation which can be extended and/or slightly modified to represent various settings and design issues for the after-sales service network. In our computational analysis, we consider a set of scenarios; we find an optimal solution for each scenario using this mathematical programming formulation. The existing system with the same number of facilities, assignments of repair vendors to the warehouses and the distribution center, and predetermined routes is the benchmark scenario. The aim of studying other scenarios is to find the optimum number of facilities and their locations, the assignment of repair vendors to the warehouses and the distribution center, and assignment of the suppliers to the facilities.
It is, indeed, impractical to solve the problem with 531 repair vendor locations distributed in 10 regions considering their demand for more than 44000 SKU spare parts supplied by 93 suppliers. Therefore, we first implement a major aggregation scheme in order to reduce the problem size significantly while avoiding loss of accuracy for optimal solutions at the network-wide decision level.
6 Data aggregation
The ERP system of the company tracks all activities regarding the after-sales service operations at the warehouse-to-customer level. Within the scope of our study, we analyze the flow of commodities over the network by consolidating for a pre-specified length of the time period and aggregating with respect to parts and facility locations. In this respect, the level of both aggregation and consolidation is important as we do not want to sacrifice from accuracy of the data used in the mathematical model.
The company provided us with the relevant data including the suppliers of and weekly volumetric demand for the parts, locations of existing facilities, locations of repair vendors, operational costs, transportation costs and other costs associated with candidate facility locations.
Starting with over 44000 SKUs and almost 700 facility locations within a 3-level hierarchical network of facilities, we reduce the problem size severely by a series of aggregations. Such model aggregation approaches are widely used not only to find the trade-off between detail level to incorporate and model tractability but also to facilitate solvability of the large-scale optimization model (Rogers et al, 1991).
Company’s commitment to serving customers within 3 days turns out to be a major concern in determining the length of the planning horizon. Supposing that each repair vendor is served twice weekly, we assume the length of the planning horizon as half week. The length of the planning horizon also implies the type of data to retrieve during the aggregation process in order to minimize the loss of accuracy.
6.1 Commodity aggregation for supply and demand
According to the demand data in 2013, there are 44408 distinct spare part SKUs that are procured via 93 suppliers. When all parts delivered by a supplier have an identical flow through the supply chain, modeling each separately is superfluous (Ballou, 2001). Hence, we also use an aggregation scheme based on their suppliers. When all parts provided by the same supplier are represented with only one aggregated item, the number of spare parts reduces to 93. The effect of such commodity aggregation on the designed supply chain may need further analysis when inhomogeneous commodities are grouped and attributes of individual products are lost in averages (Klose and Drexl, 2005). For each supplier, our spare parts are homogenous in terms of the transportation costs and warehouse handling costs but they differ in terms of demand, value and volume. To mitigate the unfavorable effects of commodity aggregation on the after-sales network design, for each supplier, each aggregated item represents a consolidation of all associated SKUs over a half-week planning horizon.
Out of 93 suppliers, 9 internal suppliers have a share of 62% in total procured volume while external suppliers provide 34%. Although internal suppliers and import suppliers shall not be ignored at any stage of the analysis, some external suppliers can be aggregated as a single external supplier as their transportation costs are incurred by themselves. Given that 56 (out of 83) external suppliers contribute to only 1% of the total procurement, firstly, they are aggregated as a fictitious external supplier. The largest supplier provides 33% of the total volume from the external suppliers; a Pareto analysis would demonstrate that few external suppliers have a significant contribution to spare part procurement operations. Among the remaining suppliers, the largest six provide 80% of total volume and a subset of 7 external suppliers (including the largest six) covers 80% of total spare parts’ procurement costs. In addition, we also analyze the coefficient of variation (CoV) in the annual volume data for each major external supplier and other suppliers which are likely to be included in the major external supplier set. As a result, we include an 8th supplier so that we work with a set of suppliers that are heterogeneous with respect to their CoV. Eventually, we leave 9 internal suppliers, 8 major external suppliers, one fictitious external supplier and one import supplier.
Four of the internal suppliers located at the same location also consolidate their outbound transportation and ship the parts to the distribution center together. Combining such geographically proximate sources of supply into a single supply source is commonly legitimate and suitable (Geoffrion et al, 1982). Therefore, these four internal suppliers’ locations are considered as the same and consolidated into a single major internal supplier. Eventually, the aggregated system works with 16 different major suppliers. As a result, aggregation of parts with respect to suppliers and aggregating suppliers into 16 distinct suppliers, we have 16 different commodity types with one-to-one correspondence with suppliers. Therefore, \( \left| I \right| = \left| S \right| \).
In order to calculate a half-week volumetric demand (\( D_{ri} \)) for each of 532 demand points (531 repair vendors and one export) for the 16 aggregated spare parts, we take the simple arithmetic average of 104 half-week realizations in 2013.
6.2 The distribution center and warehouses
The existing after-sales services network comprises of one distribution center (consisting of 3 very close distribution centers combined together) and 8 warehouses.
Facility capacities are projected as upper bounds on their inbound material handling capacity. For the distribution, we sum up the volumetric flow from the suppliers for each calendar week. Out of 52 weekly inbound flows, we take the maximum and divide it by two to estimate half-week capacity figures (C d ). For each warehouse w, we use the same approach to calculate (C w ) considering the flow from the distribution center.
We propose 15 candidate locations for the new warehouses. These candidate locations are determined by considering the major cities in Turkey which do not have a warehouse in the existing system. They are selected based on factors such as the existing repair vendors, spatial density of the warehouses in a region, development of related industry, rate of population growth and land availability. The company suggested the use of a representative warehouse as a prototype. Therefore, inbound handling capacities are set equal to that of the representative for all candidates.
Monthly operating cost is provided by the company only for the representative warehouse. In order to calculate the operating cost for each warehouse (f w ) and the distribution center (f d ), we assume that operating costs and the size (m2) of facilities are directly proportional.
6.3 Transportation costs
The company keeps track of the transportation costs from the (internal) suppliers to distribution center per trip basis. Given the transportation costs for one trip from each internal supplier to the distribution center with one truck, we calculate the volumetric transportation cost per km as \( T_{avg}^{d} \). Then, the transportation cost for each internal supplier per volumetric unit t sd is calculated by multiplying the weighted average cost \( T_{avg}^{d} \) with the distance from the internal supplier to the distribution center. We use the same approach for t sw and t dw calculations.
Transportation costs of deliveries to repair vendors depend on two factors: geographical type of the repair vendor and transportation mode. Considering the geographical type, vendors are classified as either inner city or suburban. There are two choices for alternative transportation modes: truck and freight carrier. The company calculates and accrues this cost on per trip basis. Recall that each repair vendor is serviced once during the half-week planning horizon. Therefore, the corresponding transportation cost is independent of the amount (quantity or volume) of the half-week procurement. Given the 2013 data, we can calculate p wr1 as the trip cost from a warehouse w to vendor r using truck transportation with delivery routes and p wr2 as that of freight carrier option.
Table 3 summarizes how the large-scale real-life problem is transformed into a smaller scale for our problem setting.
7 Computational analysis
We conduct a scenario-based approach for the computational analysis in order to see the effect of decentralization on the network configuration and change of transportation mode on the system-wide transportation cost. The problem is solved optimally using the mathematical formulation for each scenario. The existing system (Scenario 1) is a highly centralized network and is used as the benchmark scenario with the following characteristics:
-
All suppliers (including the import location) deliver the spare parts to the distribution center (not to any other facility).
-
Distribution center supplies the spare parts to all warehouses (including the export location) as well as repair vendors in both Istanbul regions.
-
Warehouses serve only repair vendors which are assigned to them.
-
Each repair vendor is served by only one facility, i.e. single sourcing is enforced.
-
Predetermined routes are used to deliver the spare parts from the warehouses to repair vendors. Each repair vendor is included in only one route.
-
A warehouse cannot deliver/receive parts to/from another warehouse.
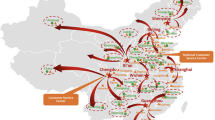
With each alternative scenario, the optimal network design is obtained by considering 15 new (candidate) warehouse locations. In a less centralized distribution network, internal suppliers send spare parts to the warehouses bypassing the distribution center. A scenario is different from another by also the mode of transportation to vendors. In Scenario 2, transportation to vendors is only through fixed routes as in the existing system. While direct shipment to vendors is done by trucks only in Scenario 3 and freight carrier services in Scenario 4, Scenario 5 considers both direct shipment with trucks or freight carriers. Schematic representations of scenarios are presented in Figure 1 where (b) corresponds to all of Scenario 2, Scenario 3 and Scenario 4 as they all allow single transportation mode in contrast to Scenario 5 depicted in (c).
In Scenario 1 and Scenario 2, 73 predetermined routes are used for delivery to repair vendors. We calculate the total distance from designated warehouses to each repair vendor on the route using a nearest neighbor algorithm and calculate the total load on a route as the sum of the expected half-week volumetric demands which should not exceed the corresponding vehicle capacity. There is a different routing system for six inner-city routes. These repair vendors’ total demands are usually higher than the others. Indeed, even a vehicle with maximum volume capacity may not meet the total demand on a single route with other vendors. When vehicle capacity is exceeded, new sub-routes are generated with a modified nearest neighbor algorithm.
The optimal solution to the integer programming problem of each scenario is obtained by GUROBI 5.6.3 on MATLAB R2012b using an Intel Core i3 processor with 2.40 GHz speed, 4 GB RAM and 64-bit Windows 7 operating system. Optimal solutions are found within 5 to 30 min of computation time. For each scenario, we evaluate the solution based on total cost and percentage share of cost items. We also investigate the optimum number and location of warehouses. We compare the results of all scenarios with each other.
The results for all scenarios are summarized in Table 4. Total cost is firstly decomposed as transportation costs and facility costs. While transportation cost is further decomposed based on delivery destination, facility operating cost is presented based on each facility type. We present delivery costs to repair vendors separately from delivery costs to the distribution center and warehouses, since they differ for each scenario with respect to given routes as well as mode of transportation.
Table 4 shows that 83% of total cost in the existing system is due to facility operating costs that include also rental costs. Moreover, it is easily observed that around 81% of facility operating cost is associated with the distribution center. As 68% of the total transportation cost is due to transportation costs to the repair vendors, there seems to be an opportunity for improvement in transportation costs through new transportation options for deliveries to repair vendors.
Scenario 2 focuses on keeping the current set of predetermined delivery routes to the repair vendors as they are. The mathematical model is used to optimize the network according to the existing delivery scheme in a less centralized network with new warehouse candidates. An optimal solution keeps three of the existing warehouses open while the remaining five are closed. The distribution center is not closed due to the constraint which blocks the external suppliers to directly meet the demand of warehouses. In contrast to the existing system where none of the suppliers may deliver parts to warehouses other than the distribution center, internal suppliers deliver to all facilities in the optimal solution. 93.13% of the total facility cost is due to the distribution center operating cost. Transportation to the repair vendors using the predetermined routes constitutes 91% of the total transportation costs. In this respect, it is worth to further analyze how the cost allocation would change in the other scenarios where delivery to repair vendors uses alternative transportation schemes or modes.
In Scenario 3, delivery to repair vendors is made by direct shipment with trucks. We aim to observe the difference between delivery by predetermined routes and delivery by trucks. In the optimal solution, the distribution center and 8 warehouses serve the repair vendors. Two of the existing warehouses are closed, and two new warehouses are opened. Total transportation cost is 29% of total network cost. Furthermore, transportation costs to the repair vendors are higher than other transportation costs. Since each facility has to serve repair vendors by individual truck shipments, the cost of transportation to serve a repair vendor is unavoidably higher than the transportation cost due to routing trips.
In Scenario 4, delivery to vendors is made by freight carrier services. In the optimal solution, there are no warehouses. All shipments to repair vendors are done directly from the distribution center to vendors. Transportation to vendors is not as less costly as it is in Scenario 2; yet, the additional savings from the facility costs compensate partially for the difference. The network structure is simplified as there are no warehouses, and it is completely centralized.
We allow both direct shipment with trucks and using freight services for delivery to the repair vendors in Scenario 5. We still enforce the single-sourcing rule where a repair vendor can be served from only one facility and by a single transportation mode. In the optimal solution, there is only one operating facility, which is the distribution center, as in Scenario 4. The solution again consists of a completely centralized network where the distribution center fulfills the orders from all repair vendors either by trucks or with third-party freight services. Although it is an extremely centralized network, total network cost is lower than the other four scenarios. The facility operating cost is remarkably lower than the other scenarios. However, the high percentage of the total cost is due to facilities. Total transportation cost, which is 23% of the total cost, includes transportation costs to the repair vendors and transportation costs to the distribution center from suppliers. Most common transportation mode is freight for repair vendor deliveries. Therefore, 88% of the transportation costs to the repair vendor are due to freight transportation.
The total cost of Scenario 2 is 11% lower than the total cost of Scenario 1. This is mainly due to a decrease in the number of facilities (from 8 to 4). Total facility operating cost of Scenario 2 is 13% lower than total facility operating cost of Scenario 1. In Scenario 2, all internal suppliers deliver parts directly to the warehouses and the distribution center is not a transport location between suppliers and warehouses. Therefore, transportation cost from suppliers to the facilities is lower than the one in Scenario 1. Because of the decrease in the number of facilities, transportation cost to the repair vendors is higher than Scenario 1 while the difference in the total cost is not significant.
Scenario 3 has the highest total cost. There is slight difference between Scenario 1 and Scenario 3 with respect to facility costs. Total transportation cost to repair vendors is 104% higher than Scenario 2 due to the usage of direct shipment. Since internal suppliers deliver parts to warehouses without using the distribution center, transportation cost between suppliers and facilities and the distribution center and warehouses is extremely low.
Scenario 4 is almost as competitive as Scenario 2 although there is only limited choice of transportation mode selection. As in Scenario 2, the facility operating costs decrease, and it decreases further with no warehouses in between the distribution center and repair vendors. Total cost is higher than that in Scenario 2, but still 9% lower than Scenario 1.
The total cost of Scenario 5 is 12% lower than Scenario 1. Although total transportation cost is not the lowest, Scenario 5 has the lowest total cost. Only the distribution center sends parts to the repair vendors either by trucks or with third-party freight services. Therefore, total facility cost is lower than the others.
Rather than the total cost of the network, the company focuses on the applicability of the network configurations. For Scenario 2, they take into account facility opening and closing decisions. However, they have concerns about operational challenges of transportation between internal suppliers and warehouses. The company wants to use third-party freight service transportation mode for repair vendor deliveries as promoted in both Scenario 4 and Scenario 5. In this respect, they also intend to investigate the applicability of deliveries from internal suppliers to the repair vendors by freight.
Alternative scenarios are expected to represent a less centralized network configuration in particular since internal suppliers may send parts directly to warehouses bypassing the distribution center and warehouses while both distribution center and warehouses can satisfy vendors’ orders. However, not all optimal solutions result in a less centralized network. In Scenario 4 and Scenario 5, warehouses are completely eliminated and the only facility to serve the repair vendors is the distribution center. Accordingly, when the solutions of the original five scenarios are investigated in detail, we observe that some vendors may not be serviced by the facilities within a reasonable time. For instance, a repair vendor in Şırnak (on the southeast corner) is 1830 km away from the distribution center. It is clear that a delivery to this vendor cannot be made even in two days.
In order to increase responsiveness, a next-day delivery policy shall be enforced. The imposed time limit on the delivery is only one day such that orders placed during any half-week period will be shipped on the first day of the next half-week period for each vendor. Most freight services promise a next-day delivery within 600 km. Similarly, direct shipments with trucks can be achieved approximately within the same distance due to labor regulations and traffic rules. In this respect, we solve the problem for each scenario with freight services and/or direct truck shipment (Scenario 3, Scenario 4 and Scenario 5) by considering a distance limit of 600 km between a vendor and the facility it is assigned to. The results of these experiments are given in Table 5.
Optimal solutions of the scenarios react to the new responsiveness criterion as follows:
-
The original solution to Scenario 3 does not include any repair vendor assigned to a facility that is farther than 600 km; therefore, the solution is exactly the same.
-
In Scenario 4, three warehouses are opened; the costs associated with facilities increase. While freight carrier costs stay the same, the total cost of the solution increases by nearly 6%.
-
Transportation costs are affected directly in Scenario 5; the solution requires three new warehouses in order to get closer to repair vendor locations. Costs due to facilities increase while transportation costs decrease. New facilities use more direct truck shipment than carrier services; this replacement clearly changes the share of each mode in the total transportation costs. The change in total cost is 3.3%.
As expected, a 600-km-distance limit may increase the system-wide costs due to the trade-off between increased responsiveness and networks costs.
8 Conclusion and future research
In this study, we present a generic mathematical model for a network design problem of after-sales services of a household appliances manufacturer. The mathematical model is depicted as a single objective mixed integer linear programming problem formulation for a static multi-commodity, multi-level network design problem. The objective function of the problem is total cost minimization. We work with a large-scale data set. A series of aggregation and consolidation techniques are employed to transform this large-scale data into a smaller scale without sacrificing accuracy. Various estimation methods are used in order to decrease the complexity of after-sales services network. Since major motivation of this study is to simplify the data as much as possible and to decrease the complexity of the problem, we prefer a scenario-based approach to focus on the network design decisions and reflect decisions on the transportation scheme.
We evaluate different network configurations through our scenario-based approach. Five different scenarios are created in order to evaluate alternative configurations and transportation scheme along with the mode choice. To make use of the mathematical model, we slightly modify decision variables, constraints and parameters of the basic formulation according to each scenario.
The solution obtained from Scenario 2 where deliveries are made by predetermined routes is reasonable as well as that of Scenario 4. Even better results are obtained when direct shipments by trucks and freight carrier services are used simultaneously. Scenario 5 has the minimum total cost due to significantly lower facility operating cost in comparison with other scenarios. When transportation mode selection is allowed, majority of the repair vendors are served via freight service and only a few repair vendors are served by direct shipment with trucks. Imposing a one-day delivery policy changes the total cost to some extent in all relevant scenarios while facility locations and allocation of vendors to facilities may change notably.
Initially, the company was particularly interested in possible advantages of freight carrier services without changing the network structure directly. The results show that structure of the network shall be as significant as mode of transportation used to deliver to vendors. In essence, a less centralized network with the current choice of transportation mode (using routes for delivery to repair vendors) is as competitive as a completely decentralized network where delivery to repair vendors is made by freight carrier services. In order to further test our findings, we solve the problems with 25% increase and 25% decrease in cost of transportation to vendors, both of the competitive scenarios are still robust.
Although the proposed approach is well suited for the analyzed real-life problem setting of a household appliances manufacturer, it might have a wider applicability for the design of other after-sales networks as long as the spare parts have low part criticality and the customers are not demanding same-day on-site service for a premium payment. Perhaps the most important and difficult extension would be designing an after-sales network with spare parts that have different spare parts characteristics such as their criticality, lifecycle phase and volume. As all the relevant studies including this work involve single period and single objective facility location models, further studies on formulating and solving multi-period and multi-objective versions are required. For spare parts that have high parts criticality and customers requesting same-day on-site service, the multi-objective formulations should be representing the trade-off between minimizing the network cost and maximizing responsiveness.
References
Amini MM, Retszaff-Roberts D and Bienstock CC (2005). Designing a reverse logistics operation for short cycle time repair services. International Journal of Production Economics 96(3):369–380.
Bacchetti A and Saccani N (2012). Spare parts classification and demand forecasting for stock control: Investigating the gap between research and practice. OMEGA: International Journal of Management Science 40(6):722–737.
Ballou RH (2001). Unresolved issues in supply chain network design. Information Systems Frontiers 3(4):417–426.
Boylan JE and Syntetos AA (2010). Spare parts management: A review of forecasting research and extensions. IMA Journal of Management Mathematics 21(3):227–237.
Cohen MA, Kamesam PV, Kleindorfer P, Lee HL and Tekerian A (1990). Optimizer: IBM’s multi-echelon inventory system for managing service logistics. Interfaces 20(1):65–82.
Cohen MA, Zheng Y-S and Agrawal V (1997). Service parts logistics: A benchmark analysis. IIE Transactions 29(8):627–639.
Cohen MA, Zheng, Y-S and Wang Y (1999). Identifying opportunities for improving Teradyne service-parts logistics system. Interfaces 29(4):1–18.
Cohen MA, Cull C, Lee HL and Willen D (2000). Saturn’s supply-chain innovation: High value in after-sales service. Sloan Management Review 41(4):93–101.
Cohen MA, Agrawal N and Agrawal V (2006). Winning in the aftermarket. Harvard Business Review 84(5):129–138.
Dennis MJ and Kambil A (2003). Service management: Building profits after the sale. Supply Chain Management Review 7(1):42–48.
Driessen M, Arts J, van Houtum G-J, Rustenburg JW and Huisman B (2015). Maintenance spare parts planning and control: A framework for control and agenda for future research. Production Planning & Control 26(5):407–426.
Du F and Evans GW (2008). A bi-objective reverse logistics network analysis for post-sale service. Computers & Operations Research 35(8):2617–2634.
Eskandarpour M, Nikbakhsh E and Zegordi SH (2014). Variable neighborhood search for the bi-objective post-sales network design problem: A fitness landscape analysis approach. Computers & Operations Research 52(Part B):300–314.
Eskandarpour M, Zegordi SH and Nikbakhsh E (2013). A parallel variable neighborhood search for the multi-objective sustainable post-sales network design problem. International Journal of Production Economics 145(1):117–131.
Geoffrion AM, Graves GW and Lee S-J (1982). A management support system for distribution planning. INFOR, Canadian Journal of Operational Research and Information Processing 20(4):287–314.
Hertz P, Finke GR and Schönsleben P (2012). Industrial field service network planning: Existing methods in supply chain planning and modeling and their applicability for field services. Proceedings of 2012 9th International Conference on Service Systems and Service Management (ICSSSM) 258–263.
Huiskonen J (2001). Maintenance spare parts logistics: Special characteristics and strategic choices. International Journal of Production Economics 71(1–3):125–133.
Jalil MN, Zuidwijk RA, Fleischmann M and van Nunen JAEE (2011). Spare parts logistics and installed base information. Journal of the Operational Research Society 62(3):442–457.
Klose A and Drexl A (2005). Facility location models for distribution system design. European Journal of Operational Research 162(1):4–29.
Landrieux B and Vandaele N (2012). A spare parts network design model for a digital cinema projector manufacturer. Proceedings of International Working Seminar on Production Economics (ISWPE) 2012, pp. 343–353.
Murthy DNP, Solem O and Roren T (2004). Product warranty logistics: Issues and challenges. European Journal of Operational Research 156(1):110–126.
Persson F and Saccani N (2009). Managing the after sales logistic network—A simulation study. Production Planning & Control 20(2):125–134.
Rogers DF, Plante RD, Wong RT and Evans JR (1991). Aggregation and disaggregation techniques and methodology in optimization. Operations Research 39(4):553–582.
Saccani N, Songini L and Gaiardelli P (2006). The role and performance measurement of after-sales in the durable consumer goods industries: An empirical study. International Journal of Productivity and Performance Management 55(3–4):259–283.
Saccani N, Johansson P and Perona M (2007). Configuring the after-sales service supply chain: A multiple case study. International Journal of Production Economics 110(1–2):52–69.
Şahin G and Süral H (2007). A review of hierarchical facility location problems. Computers & Operations Research 34(8):2310–2331.
Wu M-C, Hsu Y-K and Huang L-C (2011). An integrated approach to the design and operation for spare parts logistic systems. Expert Systems with Applications 38(4):2990–2997.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Altekin, F.T., Aylı, E. & Şahin, G. After-sales services network design of a household appliances manufacturer. J Oper Res Soc 68, 1056–1067 (2017). https://doi.org/10.1057/s41274-016-0142-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1057/s41274-016-0142-y