1 Introduction

Providing financial services for small–medium-sized enterprises (SMEs), Chinese City Commercial Banks (CCBs) play an important role in the regional economic development in China. Due to asymmetric information between banks and enterprises, 4 state-owned commercial banks (SOCBs) and 12 joint-stock commercial banks (JSCBs) tend to support state-owned enterprises (SOEs) and large enterprises, while ignoring small–medium-sized enterprises (SMEs). CCBs have an advantage of knowing more information on SMEs’ business operations and lend to them much as their long-term relationship with SMEs. Therefore, CCBs are always called as the third echelon as compared to 4 SOCBs and 12 joint-stock commercial banks. In recent years, CCBs have grown intensely and outperformed in making significant gains of market share while achieving high returns (Ferri, 2009). However, CCBs face at least three problems in Chinese financial service market: (1) Majority of CCBs rely heavily on their city’s economies, and only provide services for SMEs in their cities. Due to the “single city” management model, CCBs are greatly affected by the local economic development level and the credit environment. As a result, the development of CCBs is in the state of imbalance in the eastern and western parts of China. (2) In recent years, banking regulators reformed the financial system by paying more attention to the reform of state-owned commercial banks and rural credit cooperatives, but they ignored the CCBs. (3) They face the strong competition with 4 big SOCBs and 12 joint-stock commercial banks. Many CCBs are not clear about the market position. Many CCBs are keen to compete with SOCBs and JSCBs for large customers and big projects (Wang et al, 2012; Wang, 2000). (4) According to the official report by China Banking Regulatory Commission (CBRC) in 2012, the total number of CCBs is 142, and their total assets are 12346.9 billion (only about 9. 4% of Chinese banking system).

Under this situation, Merger & Acquisitions (M&As) become an inevitable choice for CCBs to become bigger and get rid of geographical restrictions (Gui, 2009; Zou, 2008; Zhu, 2007; García et al, 2009). In 2004, China Banking Regulatory Commission (CBRC) promulgated the “city commercial bank supervision and development program.” It clearly stated that CBRC supported the CCBs with good operating conditions to voluntarily restructure capital and consolidate to improve their risk-resisting ability and market competitiveness in accordance with the market principles. Accordingly, many CCBs’ M&As occur. For example, the Industrial Bank Co acquired the Foshan city commercial bank in 2004. Huishng Bank in 2005 and JiangSu Bank in 2007 are both resulted from the joint restructuring of several small CCBs.

In the current literature, many efficiency-based approaches such as accounting cost ratios (DeLong and DeYoung, 2007), cost X-efficiency (Berger and Humphrey, 1992), and profit X-efficiency (Akhavein et al, 1997; Berger, 1998), are used to measure and compare the performance of banks before and after M&As. They pointed out that there was no evidence to show efficiency gains due to mergers, obviously their findings depended on the sample data and the approach selected. Therefore, it is important and necessary to develop pre-merger planning approaches to estimate the potential gains from all possible mergers (Epstein, 2004), which can help decision makers to make a successful merger.

Recently, Data Envelopment Analysis (DEA) (see Charnes et al, 1978)—(CCR model) becomes a popular approach to investigate the potential gains from M&As. As a nonparametric approach to evaluate the efficiency of decision-making units (DMUs), its main advantage is that it does not require any prior assumptions on the underlying functions between inputs and outputs. It is a data-driven frontier analysis technique that floats a piecewise linear surface to rest on top of the empirical observations. So it can serve as a pre-merger planning tool to measure potential input savings and output improvements from mergers.

Seiford and Zhu (1999) applied an output-oriented DEA approach to examining the performance of two hypothetical banks that were resulted from two banks’ M&As. Gattoufi et al (2014) developed a new inverse DEA approach to obtain the inputs and outputs for a merged bank if an efficiency target is set. Lozano (2013) proposed a cost minimization model and obtained the potential cost saving to help decision makers to find the best partner for a horizontal cooperation. Halkos and Tzeremes (2013) applied the bootstrapped DEA approach (Simar and Wilson, 1998; Dyson and Shale, 2010) to calculating bias-corrected efficiency scores to measure efficiency gains of 45 possible bank hypothetical DMUs. All these hypothetical DMUs comprised efficient DMUs. Bogetoft and Wang (2005) used a radial input-oriented DEA model to estimate the potential gains from mergers by maximizing the proportional input reduction of the hypothetical DMU while keeping the DMU’s outputs unchanged, and found that there existed several possible mergers with potential gains. The overall potential gains were then decomposed to technical, scale, and harmony gains. However, they found that the hypothetical DMU may probably surpass the Production Possibility Set (PPS) constructed by candidate DMUs when using the input-oriented DEA model to estimate potential merger gains. In this case, one drawback of the model proposed in Bogetoft and Wang (2005) is that it may become infeasible. Färe et al (2011) proposed an output-oriented DEA approach by maximizing hypothetical DMUs’ potential revenues to identify potential partners, which can avoid the problem that the hypothetical DMUs may surpass the PPS.

However, all above approaches treat each DMU as a “black box” in M&As, but ignore the internal structure of the production process. In many real applications, DMUs may contain several production processes before achieving final outputs (Kao and Hwang, 2008; Zha and Liang, 2010; Zhou et al, 2013; Liu and Lu, 2012; Halkos et al, 2014; Aviles-Sacoto et al, 2015). Recently, Lozano and Villa (2010) estimated the potential merger gains of two DMUs with parallel structures and found that a hypothetical DMU combined by two DMUs could potentially have cost savings. Wu et al (2011) estimated the potential gains of banks in the dynamic network from the revenue perspective. This approach is extended by Wu and Birge (2012) to measure the potential merger gains of banks in serial-chain structures. The two approaches extended the pure merger efficiency decomposition to a two-stage production system after individual technical inefficiency is eliminated, but they didn’t evaluate the overall merger efficiency. Because the two approaches are from the revenue perspective, they avoid the problem of the hypothetical DMU’s outputs surpassing the PPS.

On the other hand, in many real mergers, the performance goal is set to minimize the total cost while keeping outputs at current levels. For example, Chase Manhattan Bank and Chemical Bank merged in 1995 with the purpose of cutting operational cost as the two banks are near in the same city and similar in operating business (Cattani and Tschoegl, 2002; Rhoades, 2010; Epstein, 2005). After merger, the merged bank has saved the expense of 1.5 billion US dollars including shutting down overlapped branches and lay-off staffs. Afterwards, the Chase Manhattan Bank acquired Hambrecht & Quist in 1999, and Robert Fleming & Co. in 2000 for the same cost-saving purpose. Therefore, it’s necessary to evaluate the potential merger gains from the cost perspective. But, a problem arises that the hypothetical DMU may surpass the frontier comprised by candidate DMUs. This might be one reason that not many studies considered evaluating potential merger gains from the cost perspective.

In this paper, we develop a two-stage cost efficiency model by minimizing the cost of this new hypothetical DMU while maintaining its outputs at sum of the pre-merger level of potential mergers. Considering variable returns to scale (VRS) assumption (see Banker et al, 1984), the hypothetical DMU may surpass the original Production Possibility Set (PPS). We thus propose to construct a Merger Production Possibility Sets (PPSM) to solve the problem. Then, we extend this to a two-stage structure to estimate the merger efficiency of a hypothetical DMU for the overall system and both sub-systems, and decompose the merger efficiency into technical, harmony, and scale efficiencies for the whole system and both sub-systems. To show the practicality and usefulness of the proposed approach, we apply our model to estimating the merger efficiency from mergers of CCBs.

The rest of this paper is organized as follows. Section 2 discusses the construction of the Merger Production Possibility set (MPPM) and the models to estimate the potential gains from M&As using DEA. In Section 3, the proposed approach is extended to a two-stage production system. Section 4 presents a real application of Chinese City Commercial Banks to illustrate the usefulness of the proposed approach. Conclusions and guidance for future research are given in Section 5.

2 Preliminary considerations

Let us assume there is a set of n DMUs in set \( \varTheta \). Each \( DMU_{j} \left( {j \in \varTheta } \right) \) consumes m inputs \( x_{ij} \left( {i = 1, \ldots ,m} \right) \) to produce s outputs \( y_{rj} \left( {r = 1, \ldots ,s} \right) \). These DMUs construct a production possibility set as follows:

$$ T = \left\{ {\left. {\left( {X,Y} \right) \in R^{m + s} \left| {\sum\nolimits_{j = 1}^{n} {\lambda_{j} X_{j} } \le X,\;\sum\nolimits_{j = 1}^{n} {\lambda_{j} Y_{j} } \ge Y,\;\lambda_{j} \ge 0,\;\forall j} \right.} \right\}} \right. $$
(1)

Each hypothetical \( DMU_{J} \left( {J \in \varPhi_{K} } \right) \) is defined as the merger of a set of K candidate DMUs in set \( \varPsi_{K}^{J} \), \( \varPsi_{K}^{J} \subset \varTheta, \) where, the total number of hypothetical DMUs in \( \varPhi_{K} \) is \( C_{n}^{K} \). In this paper, we define the hypothetical DMUJ as a direct pooling of the candidate DMUs, thus DMUJ’s inputs and outputs, respectively, are

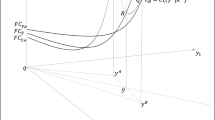
$$ X_{J} = \sum\nolimits_{{j \in \varPsi_{K}^{J} }} {X_{j} } \;{\text{and}}\;Y_{J} = \sum\nolimits_{{j \in \varPsi_{K}^{J} }} {Y_{j} } ,\quad J = 1, \ldots, C_{n}^{K} $$
(2)

As seen in Figure 1, there are n candidate DMUs using single input and single output. Two DMUs A and B have been producing technically inefficient in the past as indicated by the fact that they are not located on the efficient frontier. If they merge but continue to operate as two independent DMUs, they would spend (xA + xB) to produce (yA + yB) as a hypothetical DMU indicated by the point A + B. This is however a technically inefficient combined production. Thus, it is possible to find alternative productions that use fewer inputs to produce more outputs. Many different methods could be used to measure the potential gains of mergers. The simplest way is to use Farrell measure on the input side. The Farrell measure reduces to a simple comparison of horizontal length between A + B and C. The input of the hypothetical DMU can be scaled down with a factor. If we have access to input prices, cost efficiency could be used instead.

Figure 1
figure 1

Overall merger efficiency and technical efficiency from mergers

Full size image

The hypothetical DMU (indicated by the point A + B) discussed above is in the PPS. Thus, the point A + B could be evaluated. However, sometimes a hypothetical DMU merged by two or more DMUs may be very big and surpass the PPS. For example, two candidates A and E are merged to be the hypothetical DMU (A + E). It is clear that the point (A + E) is outside the current PPS, hence it may lead to no feasible solution to linear programs based on classical VRS models. Thus, if we measure the potential gains of mergers by Farrell measure from the input perspective, then the problem arises that the hypothetical DMUs may surpass the PPS constructed by n candidate DMUs in set \( \Theta \). Hence, it may lead to no feasible solution to linear programs based on classical VRS models.

2.1 Merger production possibility set (PPSM)

Let us consider a Merger Production Possibility Set (PPSM) as follows:

$$ \begin{aligned} M^{K} &= \left\{ (X,Y)\left| \sum\limits_{j \in \varTheta} \lambda_{j} X_{j} + \sum\limits_{J \in \varPhi_{K}} \lambda_{J} X_{J} \le X, \right.\sum\limits_{j \in \varTheta} \lambda_{j} Y_{j} \right.\\ &\quad\left. + \sum\limits_{J \in \varPhi_{K}} \lambda_{J} Y_{J} \ge Y,\sum\limits_{j \in \varTheta} \lambda_{j} + \sum\limits_{J \in \varPhi_{K}} \lambda_{J} = 1,\;\lambda_{j} \ge 0,\;\forall j \right\} \end{aligned} $$
(3)

It is constructed by n candidate DMUs and \( C_{n}^{K} \) hypothetical DMUs from the possible mergers. Considering Figure 1, it is clear that the PPSM is larger than the original PPS.

2.2 Evaluation of the potential gains from mergers

In order to measure the potential gains from mergers in the cost perspective, we first estimate the cost efficiencies for each candidate DMU and hypothetical DMU. Assume all input prices are given as \( W \in R^{\text{m}} \). The minimal cost of each candidate DMU while maintaining the output vector at the current level can be calculated by \( C\left( {Y,W} \right) = \hbox{min} \left\{ {WX^{\prime}\left| {(X^{\prime},Y) \in \left. T \right\}} \right.} \right. \) (see more details in Cooper et al, 2007).

Similarly, the minimum cost for each hypothetical DMU can be calculated by

$$ C_{J} \left( {Y_{J} ,W} \right) = \hbox{min} \left\{ {WX^{\prime}_{J} \left| {(X^{\prime}_{J} ,Y_{J} ) \in \left. {M^{K} } \right\}} \right.,\quad J \in \varPhi_{K} } \right. $$
(4)

Based on the estimated minimal cost, we can calculate efficiencies of candidate DMUs and hypothetical DMUs. The cost efficiency of any candidate \( DMU_{j0} \) producing \( y_{j0} \) is calculated by

$$ {\text{CE}}_{0} = {{C\left( {y_{0} ,w} \right)} \mathord{\left/ {\vphantom {{C\left( {y_{j0} ,w} \right)} {wx_{0} }}} \right. \kern-0pt} {wx_{0} }}, $$
(5)

where \( wx_{0} \) is the actual cost of \( DMU_{0} \) and \( C\left( {y_{0} ,w} \right) \) is calculated by \( C\left( {y_{0} ,w} \right) = \hbox{min} \left\{ {wx\left| {(x_{0} ,y_{0} ) \in \left. T \right\}} \right.} \right. \). For example, a cost efficiency of 85% suggests that the DMU can produce the same level of outputs with 15% lower costs.

Similarly, the merger efficiency of hypothetical \( {\text{DMU}}_{J} \) from the cost perspective is defined as a ratio between the minimum cost and the actual cost of producing the output Y J as follows:

$$ ME^{\text{J}} = {{C\left( {Y_{J} ,w} \right)} \mathord{\left/ {\vphantom {{C\left( {Y_{J} ,w} \right)} {wX_{J} }}} \right. \kern-0pt} {wX_{J} }} $$
(6)

As proposed by Begetoft and Wang (2005), the merger efficiency MEJ can be decomposed into technical efficiency (TEJ), harmony (mix, scope) efficiency (HEJ), and scale efficiency (SEJ) such that

$$ {\text{ME}}^{J} = {\text{TE}}^{J} \times {\text{ME}}^{J*} = {\text{TE}}^{J} \times {\text{HE}}^{J} \times {\text{SE}}^{J} $$
(7)

The calculation of technical efficiency and pure merger efficiency can be summarized (see details in Bogetoft and Otto, 2010) as follows:

$$ {\text{TE}}^{J} = {{\sum\nolimits_{{j \in \varPsi_{K}^{J} }} {C\left( {Y_{j} ,w} \right)} } \mathord{\left/ {\vphantom {{\sum\nolimits_{{j \in \varPsi_{K}^{J} }} {C\left( {Y_{j} ,w} \right)} } {wX_{J} }}} \right. \kern-0pt} {wX_{J} }},\quad J \in \varPhi_{K} $$
(8)
$$ {\text{ME}}^{*J} = {{C\left( {Y_{J} ,w} \right)} \mathord{\left/ {\vphantom {{C\left( {Y_{J} ,w} \right)} {\sum\nolimits_{{j \in \varPsi_{K}^{J} }} {C\left( {Y_{J} ,w} \right)} }}} \right. \kern-0pt} {\sum\nolimits_{{j \in \varPsi_{K}^{J} }} {C\left( {Y_{J} ,w} \right)} }},\quad J \in \varPhi_{K}, $$
(9)

where \( ME^{ *J} \) is the maximal reduction in the aggregated inputs of technically efficient DMUs in \( j \in \varPsi_{K}^{J} \) that allows the production of the output \( Y_{J} \). Hence we can save costs by merger if and only if \( ME^{ *J} < 1 \).

The harmony and scale efficiencies could be calculated as follows:

$$ {\text{HE}}^{J} = \frac{{C\left( {{{Y_{J} } \mathord{\left/ {\vphantom {{Y_{J} } K}} \right. \kern-0pt} K},w} \right)}}{{{{\sum\nolimits_{j \in J} {C\left( {y_{j} ,w} \right)} } \mathord{\left/ {\vphantom {{\sum\nolimits_{j \in J} {C\left( {y_{j} ,w} \right)} } K}} \right. \kern-0pt} K}}},\quad J \in \varPhi_{K} $$
(10)
$$ {\text{SE}}^{J} = \frac{{C\left( {Y_{J} ,w} \right)}}{{K \times C\left( {{{Y_{J} } \mathord{\left/ {\vphantom {{Y_{J} } K}} \right. \kern-0pt} K},w} \right)}},\quad J \in \varPhi_{K} $$
(11)

As these expressions show, the technical effect (learning effect) TEJ measures the reduction in costs if each DMU learns best practices but remains an independent entity. The harmony effect HEJ measures the minimal cost of the average output vector compared to the average of the costs corrected for individual learning. The scale effect SEJ measures the cost of operating at the full (integrated) scale compared to the average scale of candidate DMUs. If \( {\text{HE}}^{J} < 1\left( {{\text{SE}}^{J} < 1} \right) \), the harmony effect (scale effect) favors the merger. If \( {\text{HE}}^{J} > 1\left( {{\text{SE}}^{J} > 1} \right) \), the harmony effect (scale effect) works against the merger.

Decomposing the potential gains is important because a full-scale merger is typically not the only option available for DMUs, and alternative organizational changes may be easier to implement. The approaches above could be extended to systems composed of two processes connected in series.

3 Potential gains from mergers for a two-stage production process

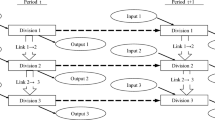
This section extends the proposed approach to a two-stage process. Consider a generic two-stage process as shown in Figure 2 for each set of n DMUs. We assume each \( {\text{DMU}}_{j} \left( {j = 1, \ldots ,n} \right) \) has m inputs \( x_{ij} \left( {i = 1, \ldots ,m} \right) \) to sub-system 1, and D outputs \( z_{dj} \left( {d = 1, \ldots ,D} \right) \) from that sub-system. These D outputs then become inputs to sub-system 2 to generate the final outputs \( y_{rj} \left( {r = 1, \ldots ,s} \right) \). Hence, \( z_{dj} \left( {d = 1, \ldots ,D} \right) \) behaves as intermediate measures.

Figure 2
figure 2

Two-stage production process for CCBs

Full size image

As discussed in Section 2, each hypothetical \( {\text{DMU}}_{J} \left( {J \in \varPhi_{K} } \right) \) is defined as the merger of a set of K candidate DMUs with a two-stage production process in set \( \varPsi_{K}^{J} \), \( \varPsi_{K}^{J} \subset \varTheta \). In this case, the total number of hypothetical DMUs in \( \varPhi_{K} \) is \( C_{n}^{K} \). The hypothetical DMU’s inputs, intermediates, and outputs, which are a direct pooling of candidate DMUs’ inputs, intermediates, and outputs, respectively, are defined as follows:

$$ X_{J} = \sum\nolimits_{{j \in \varPsi_{K}^{J} }} {X_{j} } ,\;Z_{J} = \sum\nolimits_{{j \in \varPsi_{K}^{J} }} {Z_{j} } \quad {\text{and}}\quad Y_{J} = \sum\nolimits_{{j \in \varPsi_{K}^{J} }} {Y_{j} } ,\quad J = \text{n}+1, \ldots \text{n}+C_{n}^{K} $$
(12)

In this case, the hypothetical DMUJ with a two-stage production process may surpass the PPS constructed by the n reference DMUs. To solve the problem, we add all the hypothetical DMUs in the current two-stage PPS to construct the PPSM for the two-stage network.

The PPSM for the two-stage network is defined as follows:

$$ {\rm M}{\text{T}}^{K} = \left\{ {(X,Z,Y)\left| \begin{aligned} \sum\nolimits_{j \in \varTheta } {\lambda_{j} X_{j} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\lambda_{J} X_{J} } \le X, \hfill \\ \sum\nolimits_{j \in \varTheta }^{{}} {\lambda_{j} z_{dj} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\lambda_{J} } z_{dJ} \ge Z \hfill \\ \sum\nolimits_{j \in \varTheta }^{{}} {\mu_{j} z_{dj} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\mu_{J} z_{dJ} } \le Z \hfill \\ \sum\nolimits_{j \in \varTheta } {\mu_{j} Y_{j} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\mu_{J} Y_{J} } \ge Y \hfill \\ \sum\nolimits_{j \in \varTheta } {\lambda_{j} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\lambda_{J} } = 1 \hfill \\ \sum\nolimits_{j \in \varTheta } {\mu_{j} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\mu_{J} } = 1 \hfill \\ \lambda_{j} ,\mu_{j} \ge 0,\quad j = 1, \ldots ,n \hfill \\ \lambda_{J} ,\mu_{J} \ge 0,\quad J = n+1, \ldots ,n+C_{n}^{K} \hfill \\ \end{aligned} \right.} \right\} $$
(13)

It is constructed by n candidate DMUs as well as \( C_{n}^{K} \) hypothetical DMUs with a two-stage production process, where \( \lambda_{j} \) and \( \mu_{j} \) are the weights attached to sub-system 1 and sub-system 2, respectively.

3.1 Measures of potential gains from mergers for two-stage production process

According to the definition of PPSM for a two-stage production process, we will present the two-stage cost efficiency model to estimate the minimum cost of the hypothetical DMUs. Under assumption of variable returns to scale (VRS), we get the minimum cost of the hypothetical \( DMU_{\rm L} \) with a two-stage production process as follows:

$$ \begin{aligned} \begin{array}{lll} {\hbox{min} } & {\sum\nolimits_{i = 1}^{m} {w_{i} x^{\prime}_{{iL}} } } & {} \\ {s.t.} & {\sum\nolimits_{j \in \varTheta } {\lambda_{j} x_{ij} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\lambda_{J} x_{iJ} } \le x^{\prime}_{{iL}} ,} & {i = 1, \ldots ,m} \\ {} & {\sum\nolimits_{j \in \varTheta } {\mu_{j} y_{rj} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\mu_{J} y_{rJ} } \ge y_{{rL}} ,} & {r = 1, \ldots ,s} \\ {} & {\sum\nolimits_{j \in \varTheta } {\lambda_{j} z_{dj} + \sum\nolimits_{{J \in \varPhi_{K} }} {\lambda_{J} } z_{dJ} \ge \tilde{z}_{{dL}} ,} } & {d = 1, \ldots ,D}, \\ {} & {\sum\nolimits_{j \in \varTheta } {\mu_{j} z_{dj} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\mu_{J} z_{dJ} } \le \tilde{z}_{{dL}} ,} & {d = 1, \ldots ,D} \\ {} & {\tilde{z}_{dL} \ge 0,} & {d = 1, \ldots ,D} \\ {} & {\sum\nolimits_{{{\text{j}} \in \varTheta }} {\lambda_{j} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\lambda_{J} } = 1} & {} \\ {} & {\sum\nolimits_{{{\text{j}} \in \varTheta }} {\mu_{j} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\mu_{J} } = 1} & {} \\ {} & {\lambda_{j} ,\mu_{j} \ge 0,} & {j = 1, \ldots ,n} \\ {} & {\lambda_{J} ,\mu_{J} \ge 0,} & {J = n+1,\ldots,n+C_{n}^{K} } \\ \end{array} \\ \end{aligned} $$
(14)

where \( \left( {x^{\prime}_{{iL}} ,\tilde{z}_{{dL}} ,\lambda_{j} ,\lambda_{J} ,u_{j} ,u_{J} } \right) \) are decision variables, the objective of this model is to minimize the initial cost of \( \sum\nolimits_{i = 1}^{m} {w_{i} x^{\prime}_{{iL }} } \) charged to the hypothetical \( DMU_{{L}} \) while maintaining the final output vector \( Y_{{L}} \) in sub-system 2 at the current level. Suppose the optimal solution to model (14) be \( \left( {{\text{x}}_{{{\text{iL}}}}^{' *} ,{\tilde{\text{z}}}_{{{\text{dL}}}}^{ *} ,\lambda_{\text{j}}^{*} ,\lambda_{J}^{*} ,u_{j}^{*} ,u_{J}^{*} } \right) \), then, the merger efficiencies of the hypothetical DMU L could be calculated in a manner as discussed in Section 2.

Definition 1

Merger efficiency of \( {\text{DMU}}_{{\rm L}} \) for the overall system and both sub-systems are defined as

$$ \begin{aligned} {\text{ME}}^{L} \, & = \frac{{\sum\nolimits_{i = 1}^{m} {w_{i} x^{\prime*}_{{iL}} } + \sum\nolimits_{d = 1}^{D} {w_{d} \tilde{z}}_{{dL}}^{*} }}{{\sum\nolimits_{i = 1}^{m} {w_{i} x_{{iL}} } + \sum\nolimits_{d = 1}^{D} {w_{d} z_{{dL}} } }} \\ {\text{ME}}_{1}^{{\rm L}} \, & = \frac{{\sum\nolimits_{i = 1}^{m} {w_{i} x^{\prime*}_{{iL}}} }}{{\sum\nolimits_{i = 1}^{m} {w_{i} x_{{iL}} } }} \\ {\text{ME}}_{2}^{{\rm L}} \, & = \frac{{\sum\nolimits_{d = 1}^{D} {w_{d} \tilde{z}}_{{dL}}^{*} }}{{\sum\nolimits_{d = 1}^{D} {w_{d} z_{{dL}} } }} \\ \end{aligned}, $$
(15)

where the numerator is the optimal values of model (14), and, the price of the intermediates \( w_{d} \left( {d = 1, \ldots ,D} \right) \) is set to unity as the intermediate products are produced internally and deemed to be equally important.

Proposition 1

The efficiency of any given hypothetical \( {DMU}_{{L}} \) is unity if its efficiencies for both sub-systems are unity.

Proof

Denote \( a = \sum\nolimits_{i = 1}^{m} {c_{i} x^{\prime*}_{iL}} \), \( A = \sum\nolimits_{i = 1}^{m} {c_{i} x_{iL} } \), \( b = \sum\nolimits_{d = 1}^{D} {c_{d} \tilde{z}_{dL}^{*} } \), \( B = \sum\nolimits_{d = 1}^{D} {c_{d} z_{dL} } \), then if the sub-system 1 and sub-system 2 are both efficient, we have \( {\text{ME}}_{1}^{L} = \frac{a}{A} \le 1 \) and \( {\text{ME}}_{2}^{L} = \frac{b}{B} \le 1 \) (b ≤ B). It is obvious that \( {\text{ME}}^{L} = \frac{a + b}{A + B} \le 1 \), thus the sufficient condition holds, hence proposition 1 holds.  □

Proposition 2

If \( {\text{ME}}^{L} > {\text{ME}}_{1}^{L} \), then \( {\text{ME}}_{2}^{L} > {\text{ME}}_{1}^{L} \); If \( {\text{ME}}^{L} = {\text{ME}}_{1}^{L} \), then \( {\text{ME}}_{2}^{L} = {\text{ME}}_{1}^{L} \); If \( {\text{ME}}^{L} < {\text{ME}}_{1}^{L} \), then \( {\text{ME}}_{2}^{L} < {\text{ME}}_{1}^{L} \).

Proof

As \( {\text{ME}}^{L} = \frac{a + b}{A + B} \), \( {\text{ME}}_{1}^{L} = \frac{a}{A} \le 1 \), if \( {\text{ME}}^{L} > {\text{ME}}_{1}^{L} \) then \( Aa + ab > aA + aB \), ie, \( Ab > aB \), after arrangement, \( \frac{b}{B} > \frac{a}{A} \) then \( {\text{ME}}_{2}^{L} > {\text{ME}}_{1}^{L} \). If \( {\text{ME}}^{L} = {\text{ME}}_{1}^{L} \), then \( \frac{a}{A} = \frac{a + b}{A + B} \), we have \( {\text{ME}}_{2}^{L} = {\text{ME}}_{1}^{L} \). Similarly, we can proof if \( {\text{ME}}^{L} < {\text{ME}}_{1}^{L} \), then \( {\text{ME}}_{2}^{L} < {\text{ME}}_{1}^{L} \), hence, proposition 2 holds.  □

Proposition 2 allows us to have a comparison between the merger efficiencies of different sub-systems within a two-stage process.

3.2 Decomposing the potential gains from mergers in two-stage production process

The measure of the potential gains from mergers encompasses several effects. In this section, we decompose the overall merger efficiency for the whole system and both sub-systems into technical efficiency, harmony, and scale efficiency.

The minimum cost of \( {\text{DMU}}_{0} \) producing the final outputs at the current level for each DMU individually could be estimated as follows:

$$ \begin{aligned} \begin{array}{lll} {\hbox{min} } & {\sum\nolimits_{i = 1}^{m} {w_{i} t_{i0}^{{}} } } & {} \\ {s.t.} & {\sum\nolimits_{j \in \varTheta } {\lambda_{j} x_{ij} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\lambda_{J} X_{iJ} } \le t_{i0} ,} & {i = 1, \ldots ,m} \\ {} & {\sum\nolimits_{j \in \varTheta } {\mu_{j} y_{rj} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\mu_{J} y_{rJ} } \ge y_{r0} ,} & {r = 1, \ldots ,s} \\ {} & {\sum\nolimits_{j \in \varTheta } {\lambda_{j} z_{dj} } + \sum\nolimits_{{J \in \varPhi_{k} }} {\lambda_{J} z_{dJ} } \ge p_{d0} ,} & {d = 1, \ldots ,D}, \\ {} & {\sum\nolimits_{j \in \varTheta } {\mu_{j} z_{dj} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\mu_{J} z_{dJ} } \le p_{d0} ,} & {d = 1, \ldots ,D} \\ {} & {\sum\nolimits_{j \in \varTheta } {\lambda_{j} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\lambda_{J} } = 1} & {} \\ {} & {\sum\nolimits_{j \in \varTheta } {\mu_{j} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\mu_{J} } = 1} & {} \\ {} & {\lambda_{j} ,\mu_{j} \ge 0,} & {j = 1, \ldots ,n} \\ {} & {\lambda_{J} \mu_{J} \ge 0,} & {J = n + 1, \ldots ,n + C_{n}^{K} } \\ \end{array} \hfill \\ \end{aligned} $$
(16)

where \( \left( {\lambda_{j} ,\mu_{j} ,\lambda_{J} ,\mu_{J} ,p_{d0} ,t_{i0} } \right) \) are the decision variables. The variables t i0 and p d0 denote the optimal input and intermediates for each \( DMU_{0} \) after individually technical improvement. The objective of this model is to minimize the total cost of charged to \( {\text{DMU}}_{0} \) while maintaining the final output vector \( Y_{0} \) at the current level. The VRS technical efficiencies of \( {\text{DMU}}_{0} \) for the overall system are determined as ratios of the minimum weighted sum of cost for \( {\text{DMU}}_{0} \) to the actual weighted sum of cost.

Definition 2

The technical efficiency of DMU L for the overall system and both sub-systems are defined as

$$ \begin{aligned} {\text{TE}}^{{L}} \, & = \frac{{\sum\nolimits_{{j \in \varPsi_{K}^{{L}} }} {\sum\nolimits_{i = 1}^{m} {w_{i} t_{ij}^{*} } } + \sum\nolimits_{d = 1}^{D} {\sum\nolimits_{{j \in \varPsi_{K}^{L} }} {w_{d} p_{dj}^{*} } } }}{{\sum\nolimits_{i = 1}^{m} {c_{i} x_{{iL}} } + \sum\nolimits_{d = 1}^{D} {w_{d} z_{{dL}} } }} \\ {\text{TE}}_{1}^{{\rm L}} \, & = \frac{{\sum\nolimits_{{j \in \varPsi_{K}^{{L}} }} {\sum\nolimits_{i = 1}^{m} {w_{i} t_{ij}^{*} } } }}{{\sum\nolimits_{i = 1}^{m} {w_{i} x_{{iL}} } }} \\ {\text{TE}}_{2}^{{\rm L}} \, & = \frac{{\sum\nolimits_{d = 1}^{D} {\sum\nolimits_{{j \in \varPsi_{K}^{{L}} }} {w_{d} p_{dj}^{*} } } }}{{\sum\nolimits_{d = 1}^{D} {w_{d} z_{{dL}} } }} \\ \end{aligned}, $$
(17)

where the numerator is the optimal values of model (16).

Then, the pure merger efficiency is to adjust the overall merger gains for technical efficiency effect (Bogetoft and Wang, 2005), thus we use the technically efficient DMUs as the basis for evaluating the potential gains purely from mergers as discussed in Section 2.

We could obtain the pure merger efficiency of \( {\text{DMU}}_{L} \) after calculating the technical efficiency.

Definition 3

Pure merger efficiency of \( {\text{DMU}}_{L} \) for the overall system and both sub-stages are defined as

$$ \begin{aligned} {\text{ME}}^{{*L}} \, & = \frac{{{\text{ME}}^{{L}} }}{{{\text{TE}}^{{L}} }} = \frac{{\sum\nolimits_{i = 1}^{m} {w_{i} x_{{iL}}^{*} } + \sum\nolimits_{d = 1}^{D} {w_{d} \tilde{z}_{{dL}} } }}{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{{j \in \varPsi_{K}^{{L}} }} {w_{i} t_{ij}^{*} } } + \sum\nolimits_{d = 1}^{D} {\sum\nolimits_{{j \in \varPsi_{K}^{{L}} }} {w_{d} p_{dj}^{*} } } }} \\ {\text{ME}}_{1}^{{*L}} \, & = \frac{{{\text{ME}}^{{L}} }}{{{\text{TE}}^{{L}} }} = \frac{{\sum\nolimits_{i = 1}^{m} {w_{i} x_{{iL}}^{*} } }}{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{{j \in \varPsi_{K}^{{L}} }} {w_{i} t_{ij}^{*} } } }} \\ {\text{ME}}_{2}^{{*L}} \, & = \frac{{\sum\nolimits_{d = 1}^{D} {w_{d} \tilde{z}_{{dL}} } }}{{\sum\nolimits_{d = 1}^{D} {\sum\nolimits_{{j \in \varPsi_{K}^{{L}} }} {w_{d} p_{dj}^{*} } } }} \\ \end{aligned}, $$
(18)

where the denominator is the optimal solutions of model (16) and the numerator is the optimal solutions of model (14).

After considering technical improvement and eliminating technical inefficiency we propose to obtain the harmony gains by examining how much of average input could have been saved in producing the average final outputs. The average final output bundle is calculated as follows:

$$ \bar{y}_{{rL}} = \frac{1}{K}\sum\nolimits_{{j \in \varPsi_{K}^{{L}} }} {\sum\nolimits_{r = 1}^{s} {y_{rj}^{*} } } $$
(19)

The minimum cost of producing the average of the K individually, technically efficient candidate DMUs could be estimated in the following model:

$$ \begin{aligned} \begin{array}{lll} {\hbox{min} } & {\sum\nolimits_{i = 1}^{m} {w_{i} h_{iL} } } & {} \\ {s.t.} & {\sum\nolimits_{j \in \varTheta } {\lambda_{j} x_{ij} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\lambda_{J} x_{iJ} } \le h_{iL} ,} & {i = 1, \ldots ,m} \\ {} & {\sum\nolimits_{j \in \varTheta } {\lambda_{j} z_{dj} } + \sum\nolimits_{{J \in \varPhi_{k} }} {\lambda_{J} z_{dJ} } \ge f_{dL} ,} & {d = 1, \ldots ,D} \\ {} & {\sum\nolimits_{j \in \varTheta } {\mu_{j} z_{dj} } + \sum\nolimits_{{J \in \varPhi_{k} }} {\mu_{J} z_{dJ} } \ge f_{dL} ,} & {d = 1, \ldots ,D} \\ {} & {\sum\nolimits_{j \in \varTheta } {\mu_{j} y_{rj} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\mu_{J} y_{rJ} } \overline{{y_{rL} }} ,} & {r = 1, \ldots ,s} \\ {} & {\sum\nolimits_{j \in \varTheta } {\lambda_{j} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\lambda_{J} } = 1}, & {} \\ {} & {\sum\nolimits_{j \in \varTheta } {\mu_{j} } + \sum\nolimits_{{J \in \varPhi_{K} }} {\mu_{J} } = 1}, & {} \\ {} & {\lambda_{j} ,\mu_{j} \ge 0,} & {j = 1, \ldots ,n} \\ {} & {\lambda_{J} ,\mu_{J} \ge 0,} & {J = n + 1, \ldots ,n + C_{n}^{K} } \\ \end{array} \hfill \\ \end{aligned}, $$
(20)

where hiL is the potential minimum input vector while maintaining the average of the output bundle in sub-system 2 at the current level. Model (20) minimizes the weighted sum of inputs for \( DMU_{L} \). Thus, as discussed in Section 2, the harmony efficiencies could be obtained.

Definition 4

Harmony efficiency of \( {\text{DMU}}_{{L}} \) for the overall system and both sub-systems are defined as

$$ \begin{aligned} {\text{HE}}^{\rm L} \, & = \frac{{\sum\nolimits_{{{\text{i}} = 1}}^{m} {c_{i} h_{{iL}}^{*} + \sum\nolimits_{d = 1}^{D} {c_{d} f_{{dL}}^{*} } } }}{{\frac{1}{K}\sum\nolimits_{{j \in \varPsi_{K}^{L} }} {\sum\nolimits_{i = 1}^{m} {c_{i} t_{ij}^{*} } } + \frac{1}{K}\sum\nolimits_{d = 1}^{D} {\sum\nolimits_{{j \in \varPsi_{K}^{{L}} }} {c_{d} p_{dj}^{*} } } }} \\ {\text{HE}}_{1}^{L} \, & = \frac{{\sum\nolimits_{i = 1}^{m} {c_{i} h_{{iL}}^{*} } }}{{\frac{1}{K}\sum\nolimits_{{j \in \varPsi_{K}^{L} }} {\sum\nolimits_{i = 1}^{m} {c_{i} t_{ij}^{*} } } }} \\ {\text{HE}}_{2}^{L} \, & = \frac{{\sum\nolimits_{d = 1}^{D} {c_{d} f_{{dL}}^{*} } }}{{\frac{1}{K}\sum\nolimits_{d = 1}^{D} {\sum\nolimits_{{j \in \varPsi_{K}^{L} }} {c_{d} p_{dj}^{*} } } }} \\ \end{aligned}, $$
(21)

where the denominator is the optimal solutions of model (16) and the numerator is the optimal solutions of model (20).

Next, we obtain the potential gains from size effects by calculating \( {\text{SE}}^{L} \) that measures the cost of operating at the full (integrated) scale compared to the average scale of the original entities in a two-stage production process. As discussed in Section 2, the scale efficiency can be defined as follows.

Definition 5

Scale efficiency of the hypothetical \( {\text{DMU}}_{L} \) for the overall system and both sub-systems are defined as

$$ \begin{aligned} {\text{SE}}^{L} \, & = \frac{{ME^{{*L}} }}{{HE^{L} }} = \frac{{\sum\nolimits_{i = 1}^{m} {c_{i} x_{{iL}}^{'*} } + \sum\nolimits_{d = 1}^{D} {w_{d} \tilde{z}_{{dL}}^{*} } }}{{K\sum\nolimits_{i = 1}^{m} {c_{i} h_{{iL}}^{*} } + K\sum\nolimits_{d = 1}^{D} {w_{d} f_{{dL}}^{*} } }} \\ {\text{SE}}_{1}^{L} \, & = \frac{{ME_{1}^{{*L}} }}{{HE_{1}^{L} }} = \frac{{\sum\nolimits_{i = 1}^{m} {c_{i} x_{{iL}}^{'*} } }}{{K\sum\nolimits_{i = 1}^{m} {c_{i} h_{{iL}}^{*} } }} \\ {\text{SE}}_{2}^{{L}} \, & = \frac{{ME_{2}^{{*L}} }}{{HE_{2}^{{L}} }} = \frac{{\sum\nolimits_{d = 1}^{D} {w_{d} \tilde{z}_{{dL}}^{*} } }}{{K\sum\nolimits_{d = 1}^{D} {w_{d} f_{{dL}}^{*} } }} \\ \end{aligned}.$$
(22)

The above equation presents the overall technical efficiency, overall harmony efficiency, and overall scale efficiency. It is also very important to correctly interpret the interaction between these efficiencies in both sub-systems. For example, when two banks merge, if the harmony efficiencies are very low for both sub-systems, we would consider reallocating the inputs and outputs between the banks rather than a full-scale merger.

4 Application to City Commercial Banks (CCBs) in China

4.1 Data

In China, the production system of CCBs can be treated as a two-stage process including deposit-producing process (DPP) and the profit-earning process (PEP) as shown in Figure 2. We also selected inputs, outputs, and intermediate measures similar to Wang et al (2014), as follows:

Inputs include (i) fixed assets (x 1), which refer to the asset value of physical capital, and (ii) employee expenses and other operating expenses (x 2), which refers to the payment to full-time employees hired and the expense generated during its operation. Outputs include (i) non-interest incomes (y 1), which includes fees, commissions, investment, and other business income; (ii) interest incomes (y 2), which refers to incomes that are primarily derived from loans. The intermediate measure is the bank deposits (z), which includes current deposits and time deposits.

In this case, the first system DPP shows the process of acquiring deposits in terms of its current labor, assets, and general expense. The second sub-system PEP shows the process of utilizing these deposits to generate incomes. Here, the two-stage process of the CCB system in Figure 2 shows that deposits serve as an intermediate measure which corresponds to the output of the DPP and the direct input to the PEP.

Due to the regulation proposed by China Banking Regulatory Commission (CBRC) that only CCBs with good operating conditions are allowed to merge, this paper selects the top 20 competitive CCBs in 2012 as the candidate DMUs. The summary description of the inputs, intermediate measures, and outputs is documented in Table 1. The data are derived from the Bank-scope resource package produced by Bureau Van Dijk (BVD).

Table 1 Descriptive statistics of top 20 Chinese city commercial banks of 2012
Full size table

Here, it is noteworthy that all inputs have been transferred to be cost measures, because the data already contain input price’s information. Therefore, we set each input price to unity when we apply our proposed approach to the dataset in Table 1. All units of inputs, intermediates, and outputs in Table 1 are in CNY thousand. It also shows that the data are heterogeneous. For example, the fixed assets range from 411.8 to 6627.7, with the standard deviation of 1519.488. The same phenomenon is observed with other variables, indicating that the VRS assumption is more appropriate than CRS.

4.2 Results and discussion

Given that in most real applications of bank mergers only two banks are merged, therefore, in this case study we set K = 2. Hence, the total number of hypothetical DMUs is \( C_{20}^{2} = 190 \).

The distribution of hypothetical DMUs’ merger efficiency scores under VRS assumption is shown in Table 2. It could be noted that majority of hypothetical DMUs’ merger efficiency scores are less than one for the overall system and both DPP and PEP. So there exist considerable potential merger gains for each hypothetical DMU under VRS assumption. After eliminating technical inefficiency by learning from best practice individually, only 138, 133, and 137 hypothetical DMUs’ pure merger efficiency scores are less than one for the whole system, DPP and PEP, respectively. This also indicates that the scale effects do not favor the merger which our results are consistent with Bogetoft and Wang (2005) that the gains from merging are considerably less under the VRS assumption.

Table 2 Distribution of overall and pure merger efficiencies (<100 %) under VRS assumption
Full size table

To further explain this result, we depict the distributions of hypothetical DMUs’ merger efficiency scores, technical efficiency scores, harmony efficiency scores, and scale efficiency scores for the overall system and both sub-systems in Figures 3, 4, 5, and 6. As shown in Figure 3, we can conclude that substantial potential merger gains exist for the whole system since more than 97% of the hypothetical DMUs’ merger efficiency scores are less than one. It also could be found that the distribution of the merger efficiency for the DPP lie in the left part while the distribution of the merger efficiency for the PEP lie in the right part of the axis. It indicates that the hypothetical DMUs’ have smaller merger efficiency scores in DPP than those in PEP. Thus, most bank mergers gains more from DPP than from PEP.

Figure 3
figure 3

Merger efficiency distribution under VRS

Full size image
Figure 4
figure 4

The technical efficiency distribution under VRS

Full size image
Figure 5
figure 5

The harmony efficiency distribution under VRS

Full size image
Figure 6
figure 6

The scale efficiency distribution under VRS

Full size image

Similarly, as shown in Figure 4, the hypothetical DMUs’ technical efficiency scores for the overall system are all less than one and the hypothetical DMUs’ technical efficiency scores for DPP are lower than those for PEP. Therefore, the substantial potential technical improvements exist for the whole system and most potential technical improvements gains more from DPP than from PEP. Hence, more efforts should be exerted in DPP to achieve technical improvements.

Figure 5 shows that the harmony effect favors mergers as 189 hypothetical DMUs’ harmony efficiency scores are less than one. It can also be seen that the distribution of the harmony efficiency for the DPP and PEP is the same, indicating that the potential harmony gains from both sub-systems don not have much difference.

Though the technical effect and harmony effect favor mergers, the scale effect may work against the mergers. As shown in Figure 6, 86.8% hypothetical DMUs’ scale efficiency scores for the whole system are larger than one. Moreover, 51% of hypothetical DMUs’ scale efficiency scores (larger than unity) for PEP are larger than those for DPP, meaning that cost potentially will increase. Compared to previous study in Bogetoft and Wang (2005), technical improvement and harmony effect contribute a lot to mergers, while scale effect may work against the mergers which are consistent with our study.

To further explain the most promising mergers and how the potential merger gains could be achieved, we list the top 10 most promising mergers under VRS assumption in Table 3. It could be found that harmony effect in both processes generally favors the merger while the scale effect in both processes generally works against mergers. DMU 15 (DALICITI) is small in size, with 2334.1 units fixed assets, 256800.4 units employee expenses, 173938.3 units deposits, 5559.2 units non-interest incomes, and 626.6 units interest incomes. That is why it is always a merger candidate. The results in Table 3 could be recommended to the managers when making merger decisions. For example, the A9 hypothetical DMU, which is combined by DMU 6 (CHENGDU) and DMU 15 (DALICITI), has a merger efficiency score of 38.51%. It implies that the hypothetical DMU’s potential cost saving for the whole system is 61.49% if producing the combined outputs, and the potential cost saving from DPP and PEP are 99.1 and 22.6%, respectively, ie, the merger could achieve more potential gains from DPP. Therefore, it is advisable for policy holders to exert more efforts to DPP after merging the banks.

Table 3 Merger efficiency scores of the top 10 most promising mergers under VRS assumption
Full size table

Table 3 shows that the pure merger efficiency score is 100.19%, which indicates that after individual technical improvement, the cost of hypothetical DMU could potentially increase by 0.19% if it is producing the combined outputs of these two DMUs than that of producing the output bundle separately. That is, the A9 hypothetical DMU would increase 0.19% cost than the sum of two individual technically efficient DMUs’ (DMU 6 and DMU 15) cost. The harmony effect shows that the hypothetical DMU could together save 1.3% cost by producing the average output bundles. However, the hypothetical DMU could potentially save 1.3% cost in the DPP, and 1.3% cost in the PEP due to harmony effect, so it is advisable for the management to exert effort to reallocate the outputs to create more easily produced output mixes in both DPP and PEP. We also can conclude that the scale efficiency score is 101.51%, which indicates that the hypothetical DMU would have a 1.51% increase in costs if it produces twice the average output bundle. Furthermore, the scale efficiencies for DPP and PEP are 104.16 and 101%, respectively, which means that the A9 hypothetical DMU would incur extra cost of 4.16 and 1% in DPP and PEP, respectively, if producing twice the average intermediate output bundle in DPP and twice the average output bundle in PEP. Thus, the scale inefficiency mainly comes from DPP.

Here, the positive harmony effect is dominated by the negative-scale effect. Therefore, full-scale merger of DMU 6 (CHENGDU) and DMU 15 (DALICITI) is not proper. The decomposition of the merger efficiency into technical, harmony, and scale efficiency for the overall system and DPP and PEP allow us to identify alternative ways of improving merger performance in DPP and PEP, respectively. When the technical is low, potential merger gains are possibly by learning from the best practice individually by introducing incentives to motivate efficiency. When the harmony efficiency is low, it is advised to reallocate the resources and when the scale efficiency is low, it’s favorable for a genuine merger.

5 Conclusion and direction for future research

This paper introduced a new cost efficiency two-stage model under the variable returns to scale (VRS) to evaluate the potential merger efficiency of a hypothetical DMU from the cost perspective and define merger efficiencies for the whole system and both sub-systems. The method is applied to estimate the potential merger gains from top 20 most competitive Chinese City Commercial Banks (CCBs) in 2012. When applying the method, we may face the problem that the hypothetical merged DMU surpassed the PPS under VRS. To solve the problem, we add all possible hypothetical DMUs in the traditional PPS to construct the Merger Production Possibility Set (PPSM). Then, we discuss the decomposition of merger efficiency into technical efficiency and pure merger efficiency, and the decomposition of latter into harmony efficiency and scale efficiency for the whole system and both stages. Applying the proposed approach to 190 potential mergers of CCBs involving two branches in each merging activity, we can draw the conclusion that there may exist significant potential cost saving from hypothetical DMUs for the overall system and both sub-systems under VRS assumption. This application shows that the potential gains from technical improvement and harmony effect both favor mergers, but the potential technical improvements from the DPP are more than those from the PEP, while, the scale effect may work against the merger. Thus, in most cases, the full-scale merger is not proper.

In this research, the operating circumstance of all the DMUs is consistent. In reality, the DMUs could operate under different cultural (business) environments, which may have some effect on the efficiency. The environmental factors are especially important when the factors are partial causes of inefficiency, so developing new techniques to incorporate the environmental factors into DEA model would be a promising future study.