Abstract
We provide a comprehensive analysis of the impact of probability weighting on optimal insurance demand in a unified framework. We identify decreasing relative overweighting as a new local condition on the probability weighting function that is useful for comparative static analysis. We discuss the effects of probability weighting on coinsurance, deductible choice, insurance demand for low-probability, high-impact risks versus high-probability, low-impact risks, and insurance demand in the presence of nonperformance risk. Probability weighting can make better or worse predictions than expected utility depending on the insurance demand problem at hand.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Insurance choices are important financial decisions for households and can have a significant impact on their welfare (Bhargava et al. 2017). Researchers have aspired to find a valid descriptive model of insurance choice under risk for decades to be able to predict individual behavior and conduct policy analysis. In the expected utility (EU) model, the curvature of the utility function measures the individual’s degree of risk aversion (Pratt 1964), which then drives optimal insurance demand (Mossin 1968). From a descriptive standpoint, utility curvature alone is often too rigid to explain insurance choices in the field and may require implausibly high levels of risk aversion (e.g., Sydnor 2010). Incorporating probability weighting into the decision model is a common approach to address these shortcomings (e.g., Barseghyan et al. 2013; Hansen et al. 2016; Wakker et al. 1997).
In this paper, we provide a comprehensive analysis of the impact of probability weighting on optimal insurance demand in a unified framework. Our model allows for clear comparisons to the predictions obtained under the standard EU model. We explore a number of common insurance demand problems. Specifically, we consider the effects of probability weighting on coinsurance, deductible choice, insurance demand for low-probability, high-impact (LPHI) risks versus high-probability, low-impact (HPLI) risks, and insurance demand in the presence of nonperformance risk. We are the first to formalize these problems of optimal insurance demand in one efficient model. We thus provide a comprehensive assessment of the merits and limitations of probability weighting when it comes to explaining insurance demand.
Three empirical observations motivate our study. First, people tend to “overinsure” modest risks (e.g., Sydnor 2010). Probability weighting is a potential explanation. Typical probability weighting functions imply higher insurance demand than EU when considering coinsurance in the binary loss model and for deductible choice. The reason is a substitution effect between overweighting of the loss probability and utility curvature. Second, studies have documented less demand for insurance covering LPHI risks than for insurance covering HPLI risks, which is at odds with EU predictions (e.g., Browne et al. 2015; Slovic et al. 1977). We show that, under mild conditions, probability weighting makes the same prediction as EU and is therefore not able to explain underinsurance of LPHI risks. Third, individuals are sensitive to contract nonperformance risk and reduce their insurance demand by more than EU predicts (e.g., Wakker et al. 1997; Zimmer et al. 2018). While probability weighting may appear as a promising solution, it actually implies higher insurance demand than EU under reasonable assumptions. So if anything, it exacerbates the puzzle. Together, these results reveal that the descriptive appeal of probability weighting is limited to overinsurance puzzles and does not extend to underinsurance puzzles.
We conduct most of our analysis in the simplest model of insurance demand with a binary loss risk. This simplification makes the model tractable and allows us to derive rich comparative statics without having to assume a particular functional form of the probability weighting function. We extend our results for coinsurance to optimal deductible choice. This not only shows that our results do not depend on the binary loss assumption, but also covers an important range of applications on insurance markets. We introduce decreasing relative overweighting (DRO) as a local property of the probability weighting function and collect all probabilities where it holds in the DRO region. In this region, small probabilities are overweighted more than large probabilities relative to their baseline value. We relate DRO to other properties of the probability weighting function.Footnote 1 DRO regions are large theoretically and empirically, so most loss probabilities relevant in insurance demand fall well within the region.Footnote 2 Given the usefulness of DRO for the comparative statics of insurance demand, this property may be helpful in other applications as well. In a final step, we use experimentally calibrated preferences to provide numerical illustrations of our results.
We are not the first to look at optimal insurance demand outside of the EU model. Machina (1995) analyzes the robustness of several classical results in insurance theory under non-expected utility preferences (see also Schlesinger 1997). Doherty and Eeckhoudt (1995) examine optimal insurance demand under Yaari’s (1987) dual theory. Yet others have looked at insurance demand through the lens of regret aversion (Braun and Muermann 2004), disappointment aversion (Huang et al. 2012), ambiguity aversion (Alary et al. 2013; Snow 2011), and prospect theory (Schmidt 2016). We focus on Quiggin’s (1982) rank-dependent utility (RDU) to study the role of probability weighting in insurance demand. We explicitly allow the probability weighting function to take the commonly-observed inverse S-shape (e.g., Abdellaoui et al. 2011) and abstain from parametric assumptions, which are abundant in empirical work (e.g., Barseghyan et al. 2013; Hansen et al. 2016; Harrison and Ng 2018). While some results exist (see Schmidt 1998), we are the first to bring together a whole range of insurance demand problems, including LPHI versus HPLI risks and nonperformance risk. Analyzing these issues in one unified framework allows us to take a broader perspective on the effects of probability weighting.
The paper proceeds as follows. The next section introduces the baseline model and defines DRO. In Section 3, we characterize optimal insurance demand under probability weighting, derive the substitution between overweighting and utility curvature, which resolves the overinsurance puzzle for modest risks, and extend our results to deductible insurance. In Section 4, we present situations where underinsurance has been observed. We analyze how insurance demand differs for LPHI versus HPLI risks, and study the demand effects of nonperformance risk under probability weighting. Section 5 offers numerical illustrations based on experimentally-calibrated preferences. Section 6 presents a more in-depth discussion of the literature and explains how our results offer new insights. The last section concludes.
2 Probability weighting and insurance demand
2.1 Model setup
Quiggin’s (1982) rank-dependent utility (RDU) allows us to isolate the effect of probability weighting on optimal insurance demand. We start with a simple two-state model with a binary loss. We will extend our results to deductible choice in Section 3.3 and consider three states of the world in Section 4.2 to accommodate nonperformance risk.
Let \({\widetilde{x}} = (E_1, x_1; ...; E_n,x_n)\) be an ordered prospect with outcomes \(x_1\ge ...\ge x_n\) for a partition \(\left\{ E_i \right\} _i\) of the state space into events. Under RDU, ordered prospects are evaluated according to
where u denotes an increasing and concave utility function, and \(\pi _i\) is the decision weight for event \(E_i\). Let \({\mathbb {P}}\) be the probability distribution and w the individual’s probability weighting function. Insurance covers losses and losses are bad news, so decision weights are defined by
with the convention that \(\cup _{j=n+1}^n E_j = \emptyset\).Footnote 3 To avoid violations of first-order stochastic dominance, we assume that w is increasing with \(w(0) = 0\) and \(w(1)=1\) (see Quiggin 1982; Tversky and Kahneman 1992). EU is a special case of (2) for \(w(p) = p\), because then \(\pi _i = {\mathbb {P}}(E_i)\). This enables us to isolate the effect of probability weighting on insurance decisions.
To model insurance demand, we assume the individual has initial wealth x and is subject to a potential loss of \(L<x\) which occurs with probability p. The individual chooses a level of insurance coverage to protect himself against the risk of loss. We denote the coinsurance rate by \(\alpha\) and make the common assumption that \(0 \le \alpha \le 1\). The insurer charges a loading m on top of the expected cost of insurance, so the premium is \(\alpha m pL\). Insurance is called actuarially fair for \(m =1\). If \(m >1\), the contract is actuarially unfair or loaded, and if \(m <1\), it is actuarially favorable or subsidized.Footnote 4 The no-loss state results in final wealth of \(x_1 = x-\alpha m pL\), the loss state results in final wealth of \(x_2 = x-\alpha m pL - (1-\alpha )L\).
Because \(\alpha \le 1\), final wealth in the no-loss state is never less than final wealth in the loss state. According to (2), the decision weights are then given by \(\pi _1 = 1 - w(p)\) and \(\pi _2 = w(p)\). The individual’s optimal insurance demand \(\alpha _W^*\) maximizes the following objective function:
The notation W indicates the presence of probability weighting. EU is nested in (3) for \(w(p)=p\) with the following objective function:
The notation U is short for expected utility. We can rewrite the probability weighting function as \(w(p) = p + \delta (p)\), where \(\delta (p)\) denotes the absolute amount of overweighting. It measures by how many percentage points a given probability is overweighted.Footnote 5 We can then compare the two objective functions as follows:
As long as insurance is partial (\(\alpha <1\)), probability weighting reduces the individual’s perceived welfare if and only if the loss probability is overweighted.
2.2 Decreasing relative overweighting (DRO)
We also make use of the relative amount of overweighting, which we define as follows:
It relates the absolute amount of overweighting to the value of the loss probability. For example, if \(p=0.05\) and \(p=0.10\) are both overweighted with \(w(0.05) = 0.10\) and \(w(0.10) = 0.15\), the absolute amount of overweighting is identical for the two probabilities, \(\delta (0.05) = \delta (0.10) = 0.05\). In relative terms, however, 0.05 is overweighted by more because \(\rho (0.05) = 2 > 1.5 = \rho (0.10)\).
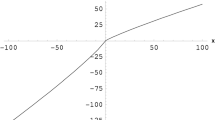
Descriptive decision theory primarily has found inverse S-shaped probability weighting functions (e.g., Abdellaoui et al. 2011; Stott 2006; Wu and Gonzalez 1996). Functions with this shape overweight small and underweight large probabilities with a unique interior fixed point where \(w(p^*) = p^*\). They are concave up to an inflection point \({\widetilde{p}}\) and convex afterward. Many functional forms have been proposed to accommodate an inverse S-shape including those in Goldstein and Einhorn (1987), Tversky and Kahneman (1992), Wu and Gonzalez (1996), Prelec (1998), and Wakker (2010). We provide an overview in Appendix A.1 and discuss some of their properties. Panel (a) in Fig. 1 shows an example of inverse S-shaped probability weighting based on the Goldstein and Einhorn functional form with parameters \(r=0.5\) and \(s=0.7\). Panels (b) and (c) depict the associated absolute and relative amount of overweighting. This motivates the following definition.
An inverse S-shaped probability weighting function based on Goldstein and Einhorn’s (1987) specification with \(r=0.5\) and \(s=0.7\) [see Equation (A.1) in Appendix A]. Parameter \(p^{*}\) denotes the fixed point, \({\tilde{p}}\) the inflection point, and \({\hat{p}}\) the upper bound of the DRO region
Definition 1
A probability weighting function has decreasing relative overweighting (DRO) at probability p if there is an open neighborhood of p where \(\rho\) is decreasing. The DRO region is the collection of all probabilities where the probability weighting function satisfies DRO.
In the DRO region, smaller probabilities are more overweighted than larger ones relative to their baseline value, just as in the example after Equation (6). If w is differentiable, the DRO region contains all probabilities where \(\rho '<0\).Footnote 6 So while overweighting can be characterized as a positive relative amount of overweighting, a condition on the level of \(\rho\), DRO is a condition on its slope. Panel (c) of Fig. 1 shows that the DRO region covers all overweighted probabilities but extends to 0.79, far beyond the fixed point and the inflection point, including many probabilities that are underweighted. Many probability weighting functions have large DRO regions, which contain the vast majority of probabilities relevant in insurance demand (see Appendix A.2). Our focus on loss probabilities in the DRO region is thus innocuous.
DRO can be related to other properties of the probability weighting function. Ryan (2006) shows that, with a concave utility function, RDU preferences are Jewitt (1989) risk-averse if and only if w(p)/p is non-increasing on (0, 1]. This is equivalent to requiring that the weak version of DRO holds globally, in which case the dual to the probability weighting function is star-shaped at 1 (see Chateauneuf et al. 2004).Footnote 7 In our analysis, we do not require DRO to hold globally. Doing so would exclude empirically relevant shapes of the probability weighting function such as an inverse S-shape because the DRO region is \((0,{\hat{p}})\) in this case with \({\hat{p}}<1\), see Proposition 7(i). DRO regions of this form imply that Tversky and Wakker’s (1995) lower subadditivity condition holds for all probabilities up to \({\hat{p}}\).
3 Overinsurance puzzles
3.1 Insurance demand under probability weighting and under EU
We first consider how optimal insurance demand depends on the loading. All formal derivations and proofs are provided in Appendix B. We obtain an upper bound \({\overline{m}}_W\) and a lower bound \({\underline{m}}_W\) on the loading. For loadings above the upper bound, the optimal level of insurance coverage is zero (\(\alpha _W^* = 0 \text { if } m \ge {\overline{m}}_W\)). Therefore, we call \({\overline{m}}_W\) the no-insurance bound. For loadings below the lower bound, full insurance coverage is optimal (\(\alpha _W^* =1 \text { if } m \le {\underline{m}}_W\)). We call \({\underline{m}}_W\) the full-insurance bound. Partial insurance is optimal for loadings between the two bounds (\(0<\alpha _W^*<1\) for \({\underline{m}}_W< m < {\overline{m}}_W\)). The two bounds are given by
The corresponding EU bounds arise as special cases of (7) for \(w(p)=p\). We denote them by \({\underline{m}}_U\) and \({\overline{m}}_U\), and let the optimal level of coverage under EU be \(\alpha _U^*\). According to Mossin (1968), full insurance is optimal when the price of insurance is actuarially fair (\(\alpha _U^{*} = 1\) if \(m = 1\)) and partial insurance is optimal when the loading exceeds unity (\(\alpha _U^{*} < 1\) if \(m > 1\)). Since the objective function in (3) nests EU, we can compare optimal insurance demand across RDU and EU.
Proposition 1
For a given utility function, overweighting (underweighting) of the loss probability:
-
(i)
increases (decreases) the full-insurance bound and the no-insurance bound, that is, \({{\underline{m}}_W} > {{\underline{m}}_U}\) and \({{\overline{m}}_W} > {{\overline{m}}_U}\) \(({{\underline{m}}_W} < {{\underline{m}}_U}\) and \({{\overline{m}}_W} < {{\overline{m}}_U})\);
-
(ii)
increases (decreases) the level of insurance demand for loadings between \(\min ({\underline{m}}_W, {\underline{m}}_U)\) and \(\max ({\overline{m}}_W, {\overline{m}}_U)\).
Furthermore, a higher loss probability:
-
(iii)
decreases the ratio \({{\underline{m}}_W} / {{\underline{m}}_U}\) for loss probabilities in the DRO region;
-
(iv)
decreases the ratio \({{\overline{m}}_W} / {{\overline{m}}_U}\) for overweighted loss probabilities in the DRO region.
Results 1(i) and 1(ii) state that overweighting of the loss probability rationalizes higher insurance demand than predicted by EU. Results 1(iii) and 1(iv) say that, in the DRO region, probability weighting drives a larger wedge between the demand thresholds the lower the loss probability. It may seem obvious that overweighting of the loss probability raises insurance demand, but there are actually two conflicting effects at work. Overweighting of the loss probability raises both the marginal cost and the marginal benefit of insurance relative to EU. Overweighting puts more weight on the loss state where marginal utility is high, and decreases the weight on the no-loss state where marginal utility is low. This raises the marginal cost of insurance because paying an additional dollar in premium is more costly in the loss state than the no-loss state. At the same time, it raises the marginal benefit of insurance because the indemnity is only received when the loss occurs. The positive net effect derives from Equation (5). Insurance transfers final wealth from the no-loss state to the loss state, which shrinks the marginal utility gap across states. Therefore, probability weighting makes the individual appreciate insurance more if and only if the loss probability is overweighted. The increase in the marginal benefit then dominates the increase in the marginal cost of insurance, and demand for insurance increases.
Proposition 1 is similar to Schmidt’s (1998) Proposition 3.1, but there are important differences. He allows for overinsurance (i.e., \(\alpha > 1\)), which we exclude by assumption, and identifies the range of loadings for which full insurance is optimal. In our case, this range is \((0,{\underline{m}}_W]\) and contains loadings where individuals would purchase more than full insurance if they had the chance to do so. Schmidt (1998) focuses on a strictly concave probability weighting function, which rules out the inverse S-shape. Our result does not require any assumptions about the curvature of the probability weighting function. Additionally, we also provide insights into the extensive margin by looking at the loading factor that chokes off insurance demand along with some comparative statics.
EU has often been criticized for its prediction of partial coverage at actuarially unfair premiums, as it tends to conflict with choices observed in the laboratory and the field (e.g., Jaspersen et al. 2021; Shapira and Venezia 2008; Sydnor 2010). Probability weighting allows us to explain the evidence. According to result 1(i), overweighting of the loss probability implies a full-insurance bound above unity so that full insurance can be optimal even when premiums are actuarially unfair. Results 1(i) and 1(ii) extend to the intensive margin: \({\underline{m}}_{W}\), \({\overline{m}}_{W}\), and \(\alpha _W^*\) are increasing in the absolute amount of overweighting. So the more the loss probability is overweighted, the larger the range of loadings above one where full insurance is in demand. Furthermore, the ratio \({{\overline{m}}_W} / {{\underline{m}}_W}\) is decreasing in p because the no-insurance bound changes at a faster rate than the full-insurance bound. So for loss probabilities in the DRO region, \({\underline{m}}_W\), \({\overline{m}}_W\), and \({{\overline{m}}_W} - {{\underline{m}}_W}\) are all decreasing in p. At lower loss probabilities, the range of loadings where insurance is in demand is wider and individuals are willing to purchase insurance at higher relative prices.
Figure 2 illustrates these results. We use the estimates in Barseghyan et al. (2013), who analyze choices for three different insurance products: automobile comprehensive, automobile collision, and homeowners insurance. They find average loss probabilities of 2.1%, 6.9% and 8.4%, and estimate a single coefficient of absolute risk aversion and a product-specific absolute amount of overweighting from the observed insurance choices. For our illustration, we use their estimates and set the loss to $1,000, which roughly corresponds to the deductible choice that the individuals in Barseghyan et al.’s (2013) study faced. Following their analysis, we use an exponential utility function, so no assumption on the individual’s wealth is necessary.Footnote 8
In Figure 2, we plot the full-insurance bound and the no-insurance bounds as a function of the absolute amount of overweighting. The gray area corresponds to RDU and the black area to EU. In all three panels, \(({\underline{m}}_W, {\overline{m}}_W)\) is above \(({\underline{m}}_U, {\overline{m}}_U)\) when \(\delta (p)\) is positive, is equal to \(({\underline{m}}_U, {\overline{m}}_U)\) when \(\delta (p)\) is zero, and is below \(({\underline{m}}_U, {\overline{m}}_U)\) when \(\delta (p)\) is negative, consistent with result 1(i). Since the bounds under probability weighting are increasing in the absolute amount of overweighting, the gray areas fan out. Comparing the panels from right to left, the gray areas become “steeper” and wider as p decreases. This illustrates the effect of the loss probability on the RDU bounds. The black EU areas do not change much at all. In fact, \({\underline{m}}_U\) is constant at 1 across panels and \({\overline{m}}_U\) increases slightly when going from right to left. This is consistent with results 1(iii) and 1(iv) because both the no-insurance bound and the full-insurance bound are more sensitive to changes in the loss probability under RDU than under EU.
Partial insurance regions under EU and under probability weighting for different values of \(\delta (p)\) for the three insurance products analyzed by Barseghyan et al. (2013). Our calculations are based on model 1b of their analysis and assume exponential utility with absolute risk aversion of 0.00063. The dashed line indicates the value of \(\delta (p)\) estimated by Barseghyan et al. for each market. The black shaded area contains the loadings where an EU individual buys partial coverage, with full insurance for loadings below and no coverage for loadings above the area. The gray shaded area is the analogous area for probability weighting
All three panels show a sizable effect of probability weighting even for modest overweighting. The dashed vertical lines in Fig. 2 represent the absolute amounts of overweighting estimated in Barseghyan et al. (2013). At these levels, the reservation price for insurance can be one and a half to four times as high as under EU. Particularly, when the loss probability is small, an individual who overweights the loss probability will likely still buy full insurance at loadings where his EU twin would not buy any insurance at all. This happens for loadings anywhere above the black area and below the gray area. Hence, probability weighting can help rationalize insurance choices when individuals exhibit higher demand than predicted by EU.
The underlying mechanism behind these observations is that RDU with standard probability weighting functions leads to increased risk aversion toward low-probability risks. The finding of increased risk aversion for losses of low probability is already part of Tversky and Kahneman’s (1992) fourfold pattern of risk attitudes. Ghossoub and He (2020) provide an overview of notions of risk aversion under RDU and also characterize their comparative versions. Requiring an RDU preference to be more risk-averse than the corresponding EU preference for all risks often imposes restrictions on the probability weighting function such as concavity (e.g., Hong et al. 1987; Ryan 2006) or dominance of the identity line (see Quiggin 1993). These restrictions rule out the common inverse S-shape. A focus on risks with a loss probability that is overweighted alleviates this issue.
3.2 Substitution between overweighting and utility curvature
Proposition 1 rests on the assumption of identical utility functions when comparing insurance demand between RDU and EU. While this helps us isolate the effect of probability weighting, empirical studies tend to find less concave utility functions when allowing probabilities to be distorted (see Barseghyan et al. 2013; Diecidue and Wakker 2002; Fox et al. 1996; Rabin 2000; Selten et al. 1999). Here, we shed light on how both motives, utility curvature and overweighting of loss probabilities, jointly explain insurance demand.
While the full-insurance bound \({\underline{m}}_W\) in (7) is constant in utility curvature, the no-insurance bound \({\overline{m}}_W\) and the optimal level of coverage \(\alpha ^*_W\) are increasing in utility curvature.Footnote 9 So, in general, optimal insurance demand reflects a substitution between utility curvature and overweighting of the loss probability. We can obtain additional insights by specifying the utility function. We use exponential or iso-elastic utility because they measure utility curvature with a single parameter and are common in empirical applications. We can then analyze combinations of utility curvature and absolute amount of overweighting that generate the same level of insurance demand. Graphically, this yields iso-insurance demand curves in the utility curvature-overweighting plane. The substitution effect makes these curves downward-sloping, and the size of their slope measures the degree of substitution. This allows us to identify factors that are associated with stronger substitution. We summarize our results in the following proposition.
Proposition 2
Let the utility function be exponential or iso-elastic utility and consider the iso-insurance demand curves in the utility curvature-overweighting plane.
-
(i)
The curves are decreasing in any case and convex if \(w(p)<0.5\);
-
(ii)
They are steeper and more convex, the higher the level of insurance demand, the lower the loss probability as long as \(w(p) < 0.5\), and the lower the loss severity.
Figure 3 shows examples of iso-insurance demand curves for iso-elastic utility. We set the loading to \(m=2\) and assume that 50% of wealth is at risk. Each panel sets a different level of insurance demand and illustrates the iso-insurance demand curve for four different loss probabilities. Per result 2(i), the curves are downward-sloping and slightly convex. In each panel, the curves are steeper the lower the loss probability. By comparing the curves across panels, we observe that higher insurance demand makes the curves steeper. This is consistent with result 2(ii). Similar results can be obtained for the no-insurance bound \({\overline{m}}_W\), which is also characterized by a substitution between utility curvature and overweighting of the loss probability. In Section 5.2, we provide a sense of magnitude for this effect using experimentally-calibrated preferences.
The substitution between overweighting and utility curvature has practical implications for the inference of preferences from insurance choices. Overweighting of the loss probability reduces the degree of utility curvature needed to rationalize a given level of insurance demand. Under EU, the utility curvature required to explain insurance choices can be implausibly large (Sydnor 2010), but allowing for overweighting renders more sensible estimates (Barseghyan et al. 2013). The convexity of the iso-insurance demand curves implies that this substitution effect is stronger at the extensive margin than the intensive margin. So when introducing a 1 percentage point overweighting of the loss probability, this reduces the utility curvature by more than when increasing an existing amount of overweighting by 1 percentage point. Result 2(ii) implies that probability weighting is particularly suitable as an explanation for high insurance demand against modest risks (see Sydnor 2010). These mechanisms underlie the empirical appeal of probability weighting as a descriptor of certain insurance choices in the field. As we will see in Section 4, this appeal is limited and does not extend to other types of insurance demand phenomena.
3.3 Deductible insurance
For many insurance decisions, individuals face severity risk conditional on the occurrence of loss and choose a deductible that determines how much of the risk they retain and how much they transfer to the insurer. The binary loss model does not allow us to distinguish between deductible insurance and coinsurance. Therefore, we will now introduce severity risk and consider the individual’s choice of an optimal deductible level. A caveat to our analysis is that a straight deductible is not necessarily optimal under RDU with an inverse S-shaped probability weighting function, see Bernard et al. (2015), Ghossoub (2019) and Xu et al. (2019). However, it is a very common shape of the indemnity schedule, which is found for property losses in auto insurance and homeowners insurance. Many health plans also contain deductibles. As it turns out, our main results in Proposition 1 do not rely on the binary loss assumption and can be extended to deductible choice.
A loss occurs with probability p, and we let the loss severity \(\ell\) take values in [0, L] according to the cumulative distribution function \(F(\ell )\). We let F be continuous and assume that L is the maximum possible loss, which is the smallest value such that \(F(L) = 1\). Then, \(F(\ell ) < 1\) for all losses \(\ell < L\). The indemnity schedule is a straight deductible, \(I(\ell ) = \max (0,\ell -D)\), for deductible level D, with associated premium
The last equality is obtained via integration by parts. We thus have \(P'(D) = -mp(1-F(D))\). The individual’s optimal deductible \(D^*_W\) maximizes
see also Bernard et al. (2015). The second equality holds because w is differentiable and F is continuous, the third equality is obtained by distinguishing between losses below the deductible and losses above the deductible. The objective function under EU is a special case of (9) by setting \(w(p) = p\) such that \(w'(p) = 1\) for all p. It is given by
see also Schlesinger (2013). The three terms represent the utility if no loss occurs, the utility of losses below the deductible, and the utility of losses above the deductible. Even under EU with a concave utility function, the objective function of the deductible choice problem is not necessarily concave (see Meyer and Ormiston 1999; Schlesinger 1981). Therefore, we have to assume that both U and W are concave in D so that we can utilize the first-order approach.
In this case, we obtain an upper bound \({\overline{m}}_W\) on the loading with no insurance demand for loadings above this threshold (\(D^*_W = L\) for \(m \ge {\overline{m}}_W\)), and a lower bound \({\underline{m}}_W\) on the loading with full insurance demand for loadings below this threshold (\(D^*_W = 0\) for \(m \le {\underline{m}}_W\)). Partial insurance is optimal for loadings between the two bounds (\(0< D^*_W < L\) for \({\underline{m}}_W< m < {\overline{m}}_W\)). These results mirror what we found in the coinsurance problem. The bounds are given by \({\underline{m}}_W = w(p)/p\) and by
The full-insurance bound \({\underline{m}}_W\) is exactly the same as in the case of coinsurance. We therefore recoup the first part of Proposition 1(i): Overweighting (underweighting) of the loss probability increases (decreases) the full-insurance bound. Obviously, we then also recoup Proposition 1(iii)
The no-insurance bound \({\overline{m}}_W\) differs from the expression in Eq. (7) for coinsurance. In the deductible case, the EU no-insurance bound is
and probability weighting now has several effects on the no-insurance bound. If \(\lim _{p \rightarrow 0} w'(p) = \infty\), as is the case for many parametric classes of inverse S-shaped probability weighting functions, we have that \({\overline{m}}_W = \infty\), and probability weighting induces the individual to always buy some insurance regardless of the size of the loading. This prediction seems unrealistic. When we focus on \(w'(0) < \infty\), probability weighting raises the no-insurance bound when the loss probability is overweighted and the probability weighting function is concave on (0, p]. The same conditions ensure that probability weighting lowers the deductible compared to the level optimal for EU. A lower deductible corresponds to increased insurance demand. The next proposition summarizes.
Proposition 3
Consider the problem of optimal deductible choice for a given utility function.
-
(i)
Overweighting (underweighting) of the loss probability increases (decreases) the full-insurance bound.
-
(ii)
Probability weighting increases the no-insurance bound if \(\lim _{p \rightarrow 0} w'(p) = \infty\), or if w overweights the loss probability and is concave on (0, p].
-
(iii)
Probability weighting lowers the optimal deductible if w overweights the loss probability and is concave on (0, p].
Compared to the coinsurance case, overweighting of the loss probability now needs to be flanked by the concavity of the probability weighting function for probabilities below the loss probability. The reason is that, in addition to the effects discussed in Section 3.1, probability weighting now also affects the marginal utility of losses below the deductible because these losses are retained by the individual. Overweighting of p and concavity up to p imply that the DRO region includes (0, p]. The assumptions in Proposition 3(ii) and (iii) are thus more restrictive than the assumptions for the corresponding coinsurance results. From an empirical standpoint, however, they are still mild. They are satisfied for an inverse S-shaped weighting function for loss probabilities that are below the interior fixed point \(p^*\) and below the inflection point \({\widetilde{p}}\). Many empirical studies find \({\widetilde{p}} \ge p^{*}\) and \(p^* \approx 0.37\) (e.g., Prelec 1998) so that most loss probabilities relevant in insurance demand are covered. In this case, the prediction of higher insurance demand under probability weighting continues to hold for some loss probabilities that are between \(p^*\) and \({\widetilde{p}}\) and are thus underweighted. The appeal of probability weighting as an explanation for higher insurance demand thus extends to the case of deductible choice and is not driven by the binary loss assumption.
4 Underinsurance puzzles
4.1 LPHI versus HPLI risks
The study of low-probability, high-impact (LPHI) risks such as natural catastrophes has become a focus of the insurance economics literature. Such risks pose a major financial challenge to consumers and to society as a whole (e.g., Abadie and Gardeazabal 2003; Bouwer et al. 2007). High insurance penetration can make households and the entire economy significantly more resilient against such shocks (Von Peter et al. 2012), suggesting that insurance against LPHI risks has greater value than insurance against high-probability, low-impact (HPLI) risks. Browne et al. (2015) show that, under EU, individuals should purchase more insurance against LPHI risks than comparable HPLI risks, but observe the opposite in the data.Footnote 10 Other studies document a similar preference in favor of insurance against HPLI risks (e.g., Slovic et al. 1977).
In this section, we investigate whether probability weighting can explain this behavior. Our results thus far do not provide an answer. As long as loss probabilities are overweighted, RDU predicts higher demand against both HPLI risks and LPHI risks than EU does, see Proposition 1(i) and 1(ii). It is not clear how the two demand levels under RDU compare to each other. Our results on the effects of changes in the loss probability in Proposition 1(iii) and 1(iv) are first-order risk changes, whereas the comparison between LPHI and HPLI risks is better conceptualized as an increase in risk in the sense of Rothschild and Stiglitz (1970), which is a second-order risk change. We summarize our findings in the following proposition.
Proposition 4
Under probability weighting, the no-insurance bound \({\overline{m}}_W\), the full-insurance bound \({\underline{m}}_W\), and optimal insurance demand \(\alpha ^{*}_{W}\) are higher for LPHI risks than HPLI risks as long as the corresponding loss probabilities are in the DRO region.
Proposition 4 extends Browne et al.’s (2015) EU prediction of higher insurance demand against LPHI risks than comparable HPLI risks to probability weighting as long as DRO holds for the relevant loss probabilities. Overweighting is not required. The result holds for a probability weighting function that underweights the associated loss probabilities as long as low probabilities are relatively less underweighted than larger ones so that DRO remains satisfied. Under EU, the full-insurance bound is always one and therefore unaffected by the change from an HPLI risk to an LPHI risk but the no-insurance bound and optimal insurance demand increase.
Probability weighting and EU make the same prediction about insurance demand against LPHI versus HPLI risks – we should observe higher demand for the former than the latter, and not the other way around. Proposition 4 holds for any increasing and concave utility function, so this prediction continues to hold even if individuals who weight probabilities have less concave utility functions than their EU counterparts. As we show in Proposition 7 in Appendix A.2, DRO regions are large for common probability weighting functions and contain all loss probabilities relevant in insurance demand. The DRO condition in Proposition 4 is thus likely to be fulfilled.
Our proof relies on Rothschild and Stiglitz’s (1970) notion of an increase in risk, which presupposes equal expected losses. This may appear as a knife-edge case. In reality, the expected loss for LPHI risks is often greater than for HPLI risks, especially when considering the fat-tailed nature of catastrophic events. Extended warranties for appliances are a typical example of an HPLI risk. Jindal (2014) finds that washing machines have a 25–29% failure rate with an average repair cost of $249 and an average replacement cost of $599, resulting in an expected loss of $62–$72 for repair and $150–$173 for replacement. Flood risk is often considered an example of an LPHI risk with some degree of underinsurance. A back-of-the-envelope calculation based on aggregate data from the National Flood Insurance Program (NFIP) shows an average insured loss amount of $67,500 and an average insured loss probability of 0.8655%.Footnote 11 This results in an expected loss of $584, which exceeds the expected loss for the HPLI risk example by more than a factor of three.
Proposition 4 remains valid when LPHI risks have higher expected losses than HPLI risks as long as the utility function displays non-increasing absolute risk aversion. Standard comparative static arguments show that optimal insurance demand is then increasing in the loss severity. Both EU and probability weighting share the prediction of higher insurance demand against LPHI risks compared to HPLI risks even if we allow for differences in expected losses. Probability weighting cannot explain why researchers often find the reverse behavior in the data.
Several alternatives have been proposed to explain underinsurance of LPHI risks. One suggestion is diminishing marginal sensitivity (Schmidt 2016), though evidence of this behavioral assumption is mixed (e.g., Chung et al. 2019; Harbaugh et al. 2010; Jaspersen et al. 2021). Friedl et al. (2014) argue that social comparison can make insurance against highly correlated risks less attractive and present evidence from a laboratory experiment. Subjective probability estimates are another possibility. Recent experimental evidence suggests that underinsurance of LPHI risks is not observed when objective probabilities are provided (Bajtelsmit et al. 2015; Laury et al. 2009). Krawczyk et al. (2017) document persistent underestimation of loss probabilities for LPHI risks even if subjects learn about the risk over time. In the extreme, individuals may simply neglect rare events. Kahneman and Tversky (1979) emphasized the importance of neglect within the editing phase. Neglect or underestimation of rare events is much more common than overweighting when people make decisions based on experience as opposed to when they learn about their options from descriptions (Hertwig et al. 2004; Hertwig and Erev 2009). When people neglect rare events, lack of insurance demand is to be expected and is not at odds with probability weighting.
4.2 Nonperformance risk
Thus far, we have assumed that the insurer will follow through with the promised indemnity when a loss happens. In real life, however, promises are not always kept. Reasons for nonperformance include insurer default, claims being denied or contested, delays in the claims handling process, and contractual uncertainty when it comes to the interpretation of the insurance contract (see Schlesinger 2013; Li and Peter 2021). Experiments have shown that individuals tend to react strongly to nonperformance risk, purchasing less insurance than predicted by EU. In Wakker et al.’s (1997) hypothetical survey, respondents required a 20% premium reduction to compensate for a 1% default probability. Similar results have been documented in other hypothetical studies (Albrecht and Maurer 2000; Zimmer et al. 2009), in incentive-compatible experiments (Zimmer et al. 2018; McIntosh et al. 2019), and in the field (Cole et al. 2013).
Probability weighting appears to be a promising explanation for low insurance demand due to nonperformance risk, because the inverse S-shape will overweight the probability of the worst outcome – experiencing a loss but not receiving a payment from the insurer. Wakker et al. (1997) find that probability weighting indeed reduces the willingness to pay for insurance when nonperformance risk is present. They only consider full insurance and can therefore not speak to the demand implications of probability weighting. When considering optimal demand, we will see that probability weighting has several effects on the optimal level of coverage. From a practical standpoint, the prediction of overinsurance tends to persist even in the presence of nonperformance risk.
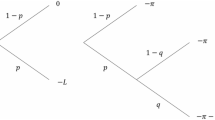
We follow the primary theoretical models of Schlesinger and von der Schulenburg (1987) and Doherty and Schlesinger (1990). The setup is the same as in Section 2.1, except that the insurer now pays the claim with probability \(q \in (0,1)\) and nonperformance occurs with probability \((1-q)\). The insurance premium is adjusted accordingly to \(\alpha m pqL\). If the claim goes unpaid, final wealth is \(x_3 = x-\alpha m pqL - L\). The individual’s objective function under EU is
where the subscript NP abbreviates nonperformance.Footnote 12 Under RDU, the individual’s insurance demand maximizes
with decision weights \(\pi _1 = 1-w(p)\), \(\pi _2 = w(p)-w(p(1-q))\) and \(\pi _3=w(p(1-q))\). We assume that the compound lottery is reduced before obtaining the decision weights.Footnote 13
Under EU, nonperformance risk invalidates most of the comparative statics of insurance demand because it introduces complex effects into the individual’s cost-benefit analysis (Doherty and Schlesinger 1990). The possibility of contract nonperformance reduces the marginal benefit of insurance because insurance is no longer completely reliable. It also increases the marginal cost of insurance because marginal utility in the nonperformance state is higher than in the other states. However, the insurance premium takes nonperformance risk into account. This represents a countervailing wealth effect, which reduces the marginal cost of insurance, because nonperformance risk makes coverage more affordable. The following proposition presents the effects of nonperformance risk on insurance demand and draws a comparison between RDU and EU.
Proposition 5
Assume the DRO region covers all probabilities up to the loss probability.
-
(i)
At the margin, nonperformance risk reduces the full-insurance bound and the no-insurance bound.
-
(ii)
At the margin, nonperformance risk reduces optimal insurance demand if the utility function exhibits non-increasing absolute risk aversion.
Let the utility function be given and assume that w overweights the loss probability and is concave on (0, p].
-
(iii)
Probability weighting leads to higher insurance demand than EU if and only if \(q > {\hat{q}}\) for an endogenous performance threshold \({\hat{q}} \in [0,1)\).
According to results 5(i) and 5(ii), nonperformance risk has the intuitive effect of reducing insurance demand if the level of nonperformance risk is small and the DRO region is large enough. Small nonperformance probabilities lower the no-insurance bound, making it less likely that individuals will purchase any amount of coverage. Small levels of nonperformance risk also lower optimal insurance demand for those loadings where coverage is in demand. In these cases, the negative effect of a less reliable insurance contract due to nonperformance risk outweighs the positive effect of a lower premium. Results 5(i) and 5(ii) contain EU as a special case, thereby extending Doherty and Schlesinger’s (1990) analysis. They find that demand effects are indeterminate when allowing for an arbitrary level of nonperformance risk, whereas we find a definitive negative effect by focusing on small levels of nonperformance risk.Footnote 14
Result 5(iii) holds for a given level of nonperformance risk, which does not have to be small. Under the stated assumptions, RDU predicts higher insurance demand than EU as long as the performance probability is large enough. In this case, probability weighting does worse than EU at explaining the underinsurance puzzle for nonperformance risk. This result may appear surprising at first sight, especially against the background of Wakker et al. (1997) who find a lower willingness to pay for insurance due to probability weighting when nonperformance risk is present. The decision weights in Equation (14) put less weight on the no-loss state (\(\pi _1 < 1-p\)) due to overweighting of the loss probability, and more weight on the nonperformance state (\(\pi _3 > p(1-q)\)) because overweighting of the loss probability and concavity of w on (0, p] imply overweighting of the nonperformance state. The probability of the intermediate state, where a loss happens and the insurance contract performs, may be overweighted (\(\pi _2 > pq\)) or underweighted (\(\pi _2 < pq\)). Overweighting occurs when q exceeds a critical level and underweighting occurs when q is below this critical level.
As a result, the marginal benefit of insurance with nonperformance risk may actually be larger under RDU than under EU as long as the performance probability is large enough because then the individual attaches sufficient weight on the intermediate state where the contract performs. So while probability weighting always increases the marginal cost of insurance relative to EU, its effect on the marginal benefit can be positive or negative. In the absence of nonperformance risk, we know from Proposition 1(ii) that the impact of probability weighting on the marginal benefit is stronger than its impact on the marginal cost. This dominance persists when introducing nonperformance risk as long as the nonperformance probability is not too large.
The assumptions on the probability weighting function in Proposition 5(iii) are the same as in the case of deductible choice, see Proposition 3(ii) and (iii). As discussed there, they are more restrictive than assuming DRO on (0, p] but are still satisfied by inverse S-shaped probability weighting functions and loss probabilities relevant in insurance demand. The important insight from Proposition 5(iii) is that for low, and thus empirically plausible, levels of nonperformance risk, probability weighting predicts higher insurance demand than EU. If EU already predicts demand that is too high compared to empirically observed behavior, probability weighting will only widen the gap between theory and evidence and make matters worse.
The restrictive assumption in Proposition 5(iii) is that we keep utility curvature fixed when introducing probability weighting. As discussed in Proposition 2, utility functions are usually less concave in the presence of probability weighting. To take this into account, we will now assume exponential or iso-elastic utility to leverage Clarke’s (2016) Theorem 2. Insurance demand with nonperformance risk is a special case of index insurance. Focusing on those cases where some insurance is purchased for some levels of risk aversion, Clarke shows that insurance demand can be strictly decreasing in risk aversion for \(m = 1\), or hump-shaped in risk aversion for \(m \ge 1\). For iso-elastic utility, we denote the relative risk aversion parameters by \(\gamma _U\) for EU and by \(\gamma _W\) for probability weighting with \(\gamma _U > \gamma _W\). If insurance demand under EU is hump-shaped in risk aversion, let \(\gamma ^*\) denote the level of risk aversion where it peaks. We then obtain the following result.
Proposition 6
Assume iso-elastic utility with parameter \(\gamma _U\) under EU and \(\gamma _W\) under probability weighting, with \(\gamma _W < \gamma _U\). Assume that w overweights the loss probability and is concave on (0, p]. Let \({\hat{q}}\) denote the threshold from Proposition 5(iii) for iso-elastic utility with parameter \(\gamma _W\).
-
(i)
For \(m=1\), if insurance demand is strictly decreasing in risk aversion and \(q > {\hat{q}}\), probability weighting predicts higher insurance demand than EU.
For \(m \ge 1\) with hump-shaped insurance demand that peaks at \(\gamma ^*\), several cases are possible.
-
(ii)
If \(\gamma _{U} \le \gamma ^{*}\) and \(q \le {\hat{q}}\), probability weighting predicts lower insurance demand than EU.
-
(iii)
If \(\gamma _{U} > \gamma ^{*}\), there is a \({\hat{\gamma }} < \gamma ^*\) so that probability weighting predicts higher insurance demand than EU for \(\gamma _{W} \in ({\hat{\gamma }}, \gamma _{U})\) and \(q \ge {\hat{q}}\), and lower insurance demand for \(\gamma _{W} < {\hat{\gamma }}\) and \(q \le {\hat{q}}\).
The proof is obtained by combining Clarke’s (2016) Theorem 2(i) and (ii) with our Proposition 5(iii). Proposition 6 presents those cases where the effect of the change in utility curvature is aligned with the effects of probability weighting. When insurance demand is hump-shaped and \(\gamma _U\) lies to the right of the peak, the critical value \({\hat{\gamma }}\) partitions \((0,\gamma _U)\) into levels of risk aversion associated with lower insurance demand and levels of risk aversion with higher insurance demand. Similarly, the threshold \({\hat{q}}\) from Proposition 5(iii) separates nonperformance probabilities where probability weighting predicts higher insurance demand from those where it predicts lower insurance demand. We obtain Proposition 6 by combining cases with the same sign. Proposition 6 also holds for exponential utility because Clarke’s Theorem 2 does and because our Proposition 5(iii) holds for any concave utility function.
Some cases remain indeterminate. Take \(m>1\) with a small level of nonperformance risk (\(q > {\hat{q}}\)) and \(\gamma _U \le \gamma ^*\) or \(\gamma _U > \gamma ^*\) but \(\gamma _W < {\hat{\gamma }}\); in this case, the decline in utility curvature predicts lower insurance demand, either because we are in the upward-sloping portion of the hump or because the decrease in utility curvature is large. However, probability weighting predicts an increase in insurance demand. The net effect then depends on the relative strength of both changes. To shed some light on those cases, we present numerical illustrations in Section 5.3.
5 Numerical illustrations based on experimental preference data
5.1 Experimental design
To speak to the magnitude of some of our analytical results, we use data from an incentivized experiment to calibrate utility curvature and probability weighting functions. We then use those preferences to illustrate our findings. For the experiment, we recruited 94 subjects from a population primarily consisting of students.Footnote 15 Subjects first completed a general knowledge questionnaire of 20 multiple-choice questions. They received 20€ in compensation for answering at least 50% of the questions correctly. Each subject then made 90 insurance-like choices over a possible loss (\(L=10\)€ or \(L=20\)€). Four of our subjects did not pass the questionnaire and are not considered further in the analysis. In 45 choices, the subject chose between a risky loss of L with probability p or a certain loss of mpL. In the other 45 choices, the subject chose between a risky gain of another 20€-L with probability p or 20€ with probability \((1-p)\), or a certain gain of 20€ \(-m pL\). Both sets of choices had the same possible combinations of p, m and L, which are displayed in Table 1. The order of all 90 choices, as well as their left/right ordering, were randomized.
5.2 The role of utility curvature and probability weighting
In Proposition 2, we showed that utility curvature and overweighting of the loss probability jointly rationalize insurance demand. To compare the relative importance of each preference motive, we first use the subjects’ decisions to estimate parameters of preference functionals at the individual level, assuming full integration of assets. We use iso-elastic utility with relative risk aversion \(\gamma\), that is, \(u(x) = x^{1-\gamma }/(1-\gamma )\) for \(\gamma \ne 1\) and \(u(x) = \ln x\) for \(\gamma = 1\), and estimate parameters for the six probability weighting functions given in Appendix A.1. Goldstein and Einhorn’s (1987, GE) functional form fits our data best, so we use it for our main analysis.Footnote 16
We then use the estimated parameters to show how differences in preferences across individuals affect predicted insurance demand. We assume \(x = 20\) and \(L = 10\) and calculate the no-insurance bound \({\overline{m}}_W\) over the range of absolute amounts of overweighting \(\delta (p)\) and utility curvature parameters \(\gamma\) observed in the subject population. For this, we hold one parameter constant at its median and vary the other parameter in the 10th, 25th, 50th, 75th, and 90th percentiles of the data, moving from lowest to highest. The top panel of Table 2 provides the percentiles of \(\delta (p)\) and \(\gamma\) in the data based on the estimated preference functionals.Footnote 17
The bottom panel of Table 2 shows the results. The second column denotes the parameter being varied. Reading from left to right, the no-insurance bound increases in the amount of overweighting of the loss probability and in utility curvature. This is consistent with the substitution between overweighting and utility curvature outlined in Proposition 2. Reading down the columns, the no-insurance bound decreases as p increases because the loss probabilities considered here are in the DRO region of \(w^{GE}\), see Proposition 7(iv) in Appendix A.2. The rightmost column of Table 2 shows the interdecile range of the no-insurance bound for the respective parameter. Three points are noteworthy. First, differences in overweighting and utility curvature can lead to sizable variation in \({\overline{m}}_W\). Second, such differences generate more variation in \({\overline{m}}_W\) at low rather than high loss probabilities. Third, \({\overline{m}}_W\) is more sensitive to changes in overweighting than changes in utility curvature at all considered loss probabilities. All in all, our findings suggest that probability weighting is the dominating preference motive because it has a stronger impact on the no-insurance bound than utility curvature, at least for our set of experimentally calibrated preferences.
The calculations in Table 2 are based on a loss that puts 50% of wealth at risk, which is high compared to most naturally occurring insurance decisions except liability and perhaps homeowners insurance when considering a total loss. In Appendix C.1, we provide an illustration for losses that put only 25% or 10% of wealth at risk. Differences in overweighting and utility curvature then lead to less variation in \({\overline{m}}_W\), but probability weighting is even more important than utility curvature in relative terms. In Appendix C.2, we repeat our illustration for different forms of the probability weighting function. While the no-insurance bound is always decreasing in p, the size of this effect varies by functional form. We provide a detailed discussion in the appendix.
5.3 Calculation of nonperformance thresholds
Propositions 5(iii) and 6 highlight the role of an endogenous performance threshold \({\hat{q}}\) to sign the effect of probability weighting on insurance demand under nonperformance risk. We will now use the experimentally calibrated preferences to calculate this threshold and provide a sense of its magnitude. We set \(x=20\) and \(L=10\) and simulate sixteen insurance decisions, using the estimated preference functionals of the subjects in our sample.Footnote 18 We vary the loss probability across four values with \(p \in \{0.01, 0.05, 0.10, 0.20\}\) and the loading across four values with \(m \in \{1.10, 1.25, 1.50, 2.00\}\). For each combination of p and m, we determine optimal insurance demand as a function of the performance probability for each individual with and without probability weighting.Footnote 19 We make two such comparisons and report them in Table 3. For the results in panel (a), we keep the utility function fixed when introducing probability weighting as in Proposition 5(iii). In panel (b), we re-estimate each individual’s preference functional when probability weighting is muted to obtain the best-fitting level of utility curvature under EU. In each comparison, we identify the value of the performance probability q where the individual’s insurance demand under probability weighting coincides with his insurance demand under EU. This is \({\hat{q}}\) for this particular individual.
For each combination of loss probability and loading, we thus obtain a distribution of \({\hat{q}}\) values across individuals. Table 3 reports the averages of these distributions. For example, the top-left value of \({\hat{q}} = 0.05\) means that, for insurance with a loading of 1.10 covering a 1% chance of loss, probability weighting will, on average, imply higher insurance demand than EU as long as claims have at least a 5% chance of getting paid. In other words, for probability weighting to rationalize lower insurance demand than EU, a nonperformance probability of more than 95% is required.
In both panels, the average performance thresholds are so low that virtually all empirically relevant levels of nonperformance risk lead to higher insurance demand under probability weighting than under EU. The average thresholds are closer to one when a high loading is coupled with a high loss probability, but these cases become less realistic at the same time. A 20% loss probability with a loading of 2 creates an insurance premium that is 40% of the insured asset’s value, and many individuals may prefer not to insure altogether, regardless of the insurer’s performance probability. Comparing the average thresholds between panels, we notice a slight increase when allowing for a different level of utility curvature. So the additional flexibility about the utility function implies that lower levels of nonperformance risk allow for RDU to predict less insurance demand than EU. However, the difference between the two panels never exceeds 5 percentage points, so in absolute terms these levels of nonperformance risk are still high.
To put things in perspective, we note that many of the loss probabilities and loading factors in Table 3 are representative of standard consumer insurance markets. The predicted homeowners loss probability in Barseghyan et al. (2013) has a mean of 8.4% and a standard deviation of 4.4%. Insurers typically operate in competitive markets with moderate loadings. A back-of-the-envelope calculation using twenty years of industry-level data from the National Association of Insurance Commissioners (NAIC 2017), shows that the mean ratio of premiums to losses (an approximation of m) for homeowners insurance is 1.39 with a maximum of 1.67. For private auto insurance, the mean is 1.31 and the maximum is 1.44.
The nonperformance probabilities implied by Table 3 are higher than those observed in practice, and in most cases much higher. For example, A.M. Best studied impairments between 1969 and 2002 and found an average annual impairment frequency of 0.8% in the U.S. property/casualty industry (Best 2004). Li et al. (2021) use rating transitions for annuity providers and show that cumulative average impairment rates can be in the double digits when allowing for long time horizons of more than 10 years and for initial ratings of B++/B or worse. Insurers with an A/A- rating or better will have a cumulative average impairment rate of less than 10% even after 15 years. In this case, almost all combinations of loss probability and loading in Table 3 predict higher insurance demand under RDU than under EU. So while the substitution between utility curvature and overweighting can resolve commonly observed overinsurance puzzles, it does not provide a good explanation for underinsurance due to nonperformance risk. If anything, it exacerbates the puzzle because RDU predicts even higher insurance demand than EU in the presence of nonperformance risk despite the fact that the probability of the nonperformance state will typically be overweighted. Contrary to the case of underinsurance of LPHI risks, neglect or underestimation of rare events does not help here. If individuals neglect nonperformance risk altogether, their insurance demand should not react much at all. Peter and Ying (2020) propose uncertainty as a potential explanation for lower insurance demand due to nonperformance risk.
6 Relationship to prior literature
Our results complement and extend the literature on probability weighting and insurance demand. Several authors have explained a preference for full insurance at actuarially unfair premiums. One explanation is based on first-order risk aversion (Schmidt 1998; Segal and Spivak 1990; Schlesinger 1997), which can be accommodated by EU (Dionne and Li 2014), but arises more prominently in RDU with a concave or convex probability weighting function, see Segal and Spivak’s (1990) Proposition 4. In a similar vein, Doherty and Eeckhoudt (1995) use Yaari’s (1987) dual theory with a concave probability weighting function to explain full insurance at unfair premiums. By assumption, these papers rule out the commonly found pattern of inverse S-shaped probability weighting (e.g., Abdellaoui et al. 2011). Our focus on binary risks allows us to be more flexible about the probability weighting function. We are also able to provide a more detailed characterization of optimal insurance demand under probability weighting and to carve out the substitution between overweighting and utility curvature explicitly, including its determinants.
Others have investigated risk sharing in markets with aggregate uncertainty under the dual theory, under RDU, or under Schmeidler’s (1989) more general Choquet Expected Utility. Schmidt (1999) characterizes efficient risk sharing under the dual theory with a concave probability weighting function. Chateauneuf et al. (2000), Tsanakas and Christofides (2006), Chakravarty and Kelsey (2015), and Carlier and Dana (2008) go beyond the dual theory but focus on convex probability weighting functions. Xia and Zhou (2016) require all individuals in the economy to have the same probability weighting function. Boonen and Ghossoub (2020) allow for inverse S-shaped probability weighting and for differences across individuals. Overall, the focus in this literature is on the characterization of Pareto optima and less on the comparative statics of insurance demand. There is usually no comparison of insurance demand for LPHI risks versus HPLI risks and no consideration of nonperformance risk.
Several empirical studies have used probability weighting to explain insurance demand. The identification strategy in Barseghyan et al. (2013) is based on a binary loss risk and approximates the utility function by a second-order Taylor expansion. Their focus is on the willingness to pay for insurance. Similar studies include Harrison and Ng (2018), Hansen et al. (2016), and Collier et al. (2021). We, in turn, derive new results about optimal insurance demand without approximating the utility function and without functional form assumptions on the probability weighting function. Contrary to the commonly held belief, results about willingness to pay do not automatically carry over to optimal demand. Chiu (2012) identifies comparability assumptions that allow him to leverage results about the effect of risk preferences on willingness to pay and apply them to the optimal demand for stochastic improvements.Footnote 20 He relies on EU. What these comparability assumptions look like under RDU is, to the best of our knowledge, unknown.
Our application of probability weighting to underinsurance problems is novel in the literature. Doherty and Schlesinger’s (1990) model of nonperformance risk has been extended to recovery conditional on default (Mahul and Wright 2007), to the insurer-reinsurer relationship (Bernard and Ludkovski 2012), to risk management instruments other than insurance (Briys et al. 1991; Schlesinger 1993), to divergent beliefs about nonperformance risk (Cummins and Mahul 2003), and to endogenous default risk (Biffis and Millossovich 2012). All of these studies are based on EU. Wakker et al. (1997) study the willingness to pay for full insurance in the presence of nonperformance risk. Probability weighting then implies a stronger negative effect of nonperformance risk than EU (see also Segal 1988). Propositions 5(i) and 5(ii) show that this negative effect persists when considering optimal demand; however, when comparing demand levels between RDU and EU, the ranking can now go either way (see Proposition 5(iii) and 6). The more plausible case is higher insurance demand under RDU than under EU, as illustrated in Section 5.3. This discrepancy highlights that findings about willingness to pay may not be applicable to optimal demand. In reality, individuals not only choose whether to buy insurance but also how much to buy, because many contracts offer different levels of coverage.
7 Implications and conclusions
In this paper, we study the effect of probability weighting on optimal insurance demand. We investigate three established empirical findings. People overinsure modest risks, underinsure LPHI risks compared to HPLI risks, and underinsure in response to nonperformance risk. We are the first to formalize these different insurance demand problems in one efficient framework, which allows us to take a broader perspective on the merits and limitations of probability weighting. In the course of our analysis, we identify decreasing relative overweighting (DRO) as a useful local property of the probability weighting function and focus on loss probabilities in the DRO region for many of our results. Given its usefulness in the context of insurance demand, we anticipate that the DRO property may turn out to be helpful in other economic applications of probability weighting as well.
Many of our results are based on a simple model of insurance demand with a binary risk of loss. This allows us to be flexible in terms of the probability weighting function. We characterize optimal insurance demand under RDU and compare it to EU. Overweighting of the loss probability increases insurance demand, which leads to a substitution between overweighting and utility curvature. We derive determinants of the intensity of this substitution effect and explain how it underlies the descriptive appeal of probability weighting as a solution to the overinsurance puzzle of modest risks (Sydnor 2010). We also extend our results for coinsurance to deductible choice and show that they are robust. When it comes to underinsurance problems, however, probability weighting has little to offer. Just like EU, it predicts higher insurance demand for LPHI risks than HPLI risks, and is therefore unable to explain lacking insurance demand against LPHI risks (Browne et al. 2015). Finally, we investigate insurance demand in the presence of nonperformance risk with probability weighting. EU has been criticized for its inability to explain how strongly individuals react to even modest levels of nonperformance risk (Cole et al. 2013; Zimmer et al. 2018). Under plausible assumptions, RDU predicts higher insurance demand than EU in such contexts, and is therefore even further away from the evidence. Collectively, our results show that the predictions of higher insurance demand due to probability weighting carries over to situations where researchers have instead documented underinsurance.
The juxtaposition of these results reveals that probability weighting is best understood as an incomplete solution for insurance demand puzzles. Its descriptive appeal depends on whether the objective is to explain overinsurance or underinsurance. The results in our paper motivate further research in this area. For example, what are the properties of a particular insurance choice that activate or deactivate probability weighting as a preference motive? How and when does probability weighting interact with other drivers of insurance choices, such as reference dependence, subjective probabilities, and the use of heuristics? Insurance markets provide a real-world laboratory to test the descriptive merits of competing models of choice under risk, and the new results in this paper are a step forward toward a better understanding of the advantages and limitations of probability weighting as a descriptive theory of insurance demand behavior.
Notes
For typical inverse S-shaped probability weighting functions, the DRO region includes all probabilities below a threshold of at least 75%. Our focus on loss probabilities in the DRO region is thus less restrictive than overweighting, because only probabilities below 40% or so are overweighted in most cases.
If only gains were involved, decision weights would be given by \(\pi _i = w\left( {\mathbb {P}}\left( \cup _{j=1}^i E_j\right) \right) - w\left( {\mathbb {P}}\left( \cup _{j=1}^{i-1} E_j\right) \right)\), with the convention that \(\cup _{j=1}^{0} E_j = \emptyset\), see Sarin and Wakker (1998). Insurance decisions have rarely been interpreted in the gain domain. Exceptions are Schmidt’s (2016) analysis based on third-generation prospect theory (see Schmidt et al. 2008) and Köszegi and Rabin’s (2007) choice-acclimated personal equilibrium.
We assume \(m < 1/p\) because otherwise purchasing any amount of insurance would be state-wise dominated by remaining uninsured. We will tighten the upper bound on m later in the analysis.
The absolute amount of overweighting \(\delta (p)\) is positive for probabilities that are overweighted and negative for probabilities that are underweighted. Some properties of \(\delta\) follow directly from properties of w, such as \(\delta (0) = \delta (1) = 0\), \(\delta (p) \in [-p, 1-p]\) for all p, and \(\delta '(p) \ge -1\) for all p where \(\delta\) is differentiable.
As long as the probability weighting function has no more than one inflection point, which holds for most functional forms including inverse S-shaped, the DRO region is connected. With two or more inflection points, the DRO region may be a collection of intervals. We exclude disconnected DRO regions to simplify the exposition.
Ghossoub and He (2020) provide an overview of notions of (comparative) risk aversion for RDU preferences and their characterization. If the probability weighting function is star-shaped at 0, the DRO region is empty because star-shapedness is equivalent to w(p)/p being non-decreasing on (0, 1].
The individuals in Barseghyan et al.’s (2013) sample choose from six auto comprehensive deductibles between $50 and $1,000, from five auto collision deductibles between $100 and $1,000, and from six homeowners insurance deductibles between $100 and $5,000.
The result for \({{\overline{m}}_W}\) is obtained by factoring out w(p)/p from (7). The first-order condition for \(\alpha ^{*}_{W}\) implies a positive relationship between utility curvature and insurance demand. Both conclusions rely on Pratt (1964), who shows that \(u'(x)/u'(x-L)\) is negatively associated with the curvature of u.
Our calculations are from 2014–2018 statistics on NFIP-insured properties posted on the FEMA homepage, https://www.fema.gov/total-policies-force-calendar-year. Average loss size is based on total loss dollars paid divided by the number of losses. Average loss probability is based on the number of losses divided by the number of policies in force.
Assuming reduction of compound lotteries (ROCL) is not innocuous (see Bernasconi 1994). Segal (1990) shows in his Theorem 2(a) that ROCL does not imply compound independence or mixture independence, so it is not at odds with RDU. Segal’s (1990) recursive RDU model allows for violations of ROCL. Recent experimental evidence suggests that this model performs worse at explaining insurance choices than conventional RDU with ROCL (see Lambregts et al. 2021).
Equivalently, higher insurance demand in response to nonperformance risk requires a sufficiently large nonperformance probability. How large exactly depends on the other parameters of the model, including utility curvature. Whether such levels of nonperformance risk are empirically relevant is unclear.
Sessions were conducted in the Munich Experimental Laboratory for Economic and Social Sciences in 2014. Subjects were recruited from the general subject pool without restrictions. See Appendix D for detailed instructions.
We include subjects with negative \(\gamma\) and thus convex utility functions in the analysis. For them, \({\overline{m}}_W\) is the loading where they are indifferent between no insurance and full insurance because individuals with a convex utility function would never purchase partial insurance. However, \({\overline{m}}_W\) is continuous in \(\gamma \in {\mathbb {R}}\) and its comparative statics with respect to \(\gamma\) and \(\delta (p)\) are similar for concave and convex utility functions.
Our results are virtually unchanged if the loss puts only 25% or 10% of wealth at risk.
We use Goldstein and Einhorn’s (1987) probability weighting function because it has the best overall fit with our data, and restrict the comparison to individuals with a concave utility function, since this is required in Proposition 5(iii) and 6 . In each insurance decision, we further discard those individuals who have the same insurance demand at all levels of nonperformance risk as no meaningful comparison is possible. This case mostly appears for combinations of high p and high m because then insurance demand is uniformly zero.
Jaspersen (2016) provides a numerical example where the individual with a higher willingness to pay optimally selects a lower level of coverage than the individual with a lower willingness to pay.
For \(r \in (2,2.6112)\), it has two inflection points and is convex-concave-convex. For \(r \ge 2.6112\), it is convex.
For monotonicity, we need to set \(s \le 1\) when \(r>1\) and \(s < {\overline{s}}\) when \(r <1\). The upper bound \({\overline{s}}\) on s is implicitly defined via \({\overline{s}}+\left[ \left( (1-r)/r\right) ^r + \left( (1-r)/r\right) ^{r-1} \right] {\overline{s}}^r = 1\). It is strictly increasing in r from \(\lim _{r \rightarrow 0} {\overline{s}} (r) = 2\) to \(\lim _{r \rightarrow 1} {\overline{s}}(r) = \infty\).
For \(r > 1\) and \(s \le (r-1)/r\), it does not have an interior fixed point. In this case, it can be convex, S-shaped, or have multiple inflection points.
This case may not arise because when \(\delta (p)\) is high enough, \({\underline{m}}_W \ge {\overline{m}}_U\).
If we had \(w'(0) \le 1\) for a probability weighting function that is concave on (0, p], then \(w(p) = \int _0^p w'(t) \, \mathrm {d}t \le w'(0) \int _0^p \, \mathrm {d}t = pw'(0) \le p\), which contradicts with overweighting of p.
A lower p decreases the marginal cost of insurance because there is less weight on the loss state (first term); a larger L increases the marginal cost of insurance because it lowers final wealth in the loss state (second term); a lower p reduces the marginal benefit of insurance because there is less weight on the loss state (third term); a larger L increases the marginal benefit of insurance because it raises the dollar amount per unit of coverage (fourth term); a larger L increases the marginal benefit of insurance because it reduces final wealth in the loss state (fifth term).
References
Abadie, A., and J. Gardeazabal. 2003. The economic costs of conflict: A case study of the Basque Country. The American Economic Review 93 (1): 113–132.
Abdellaoui, M., A. Baillon, L. Placido, and P.P. Wakker. 2011. The rich domain of uncertainty: Source functions and their experimental implementation. The American Economic Review 101 (2): 695–723.
Alary, D., C. Gollier, and N. Treich. 2013. The effect of ambiguity aversion on insurance and self-protection. The Economic Journal 123 (573): 1188–1202.
Albrecht, P., and R. Maurer. 2000. Zur Bedeutung einer Ausfallbedrohtheit von Versicherungskontrakten - ein Beitrag zur Behavioral Insurance. Zeitschrift für die gesamte Versicherungswissenschaft 89 (2–3): 339–355.
A.M. Best. 2004. A.M. Best publishes 34-year property/casualty insolvency study. Business Wire.
Baillon, A., H. Bleichrodt, A. Emirmahmutoglu, J.G. Jaspersen, and R. Peter. 2020. When risk perception gets in the way: Probability weighting and underprevention. Operations Research. https://doi.org/10.1287/opre.2019.1910.
Bajtelsmit, V.L., J.C. Coats, and P. Thistle. 2015. The effect of ambiguity on risk management choices: An experimental study. Journal of Risk and Uncertainty 50 (3): 249–280.
Barseghyan, L., F. Molinari, T. O’Donoghue, and J.C. Teitelbaum. 2013. The nature of risk preferences: Evidence from insurance choices. The American Economic Review 103 (6): 2499–2529.
Bernard, C., X. He, J.-A. Yan, and X.Y. Zhou. 2015. Optimal insurance design under rank-dependent expected utility. Mathematical Finance 25 (1): 154–186.
Bernard, C., and M. Ludkovski. 2012. Impact of counterparty risk on the reinsurance market. North American Actuarial Journal 16 (1): 87–111.
Bernasconi, M. 1994. Nonlinear preferences and two-stage lotteries: Theories and evidence. The Economic Journal 104 (422): 54–70.
Bhargava, S., G. Loewenstein, and J. Sydnor. 2017. Choose to lose: Health plan choices from a menu with dominated options. The Quarterly Journal of Economics 132 (3): 1319–1372.
Biffis, E., and P. Millossovich. 2012. Optimal insurance with counterparty default risk. Imperial College London (Working Paper).
Boonen, T., and M. Ghossoub. 2020. Bilateral risk sharing with no aggregate uncertainty under rank-dependent utility. Available at SSRN 3524926.
Bouwer, L.M., R.P. Crompton, E. Faust, P. Höppe, R.A. Pielke Jr., et al. 2007. Confronting disaster losses. Science 318 (5851): 753.
Braun, M., and A. Muermann. 2004. The impact of regret on the demand for insurance. The Journal of Risk and Insurance 71 (4): 737–767.
Briys, E., H. Schlesinger, and J.-MGv. Schulenburg. 1991. Reliability of risk management: Market insurance, self-insurance and self-protection reconsidered. Geneva Papers on Risk and Insurance Theory 16 (1): 45–58.
Browne, M.J., C. Knoller, and A. Richter. 2015. Behavioral bias and the demand for bicycle and flood insurance. Journal of Risk and Uncertainty 50 (2): 141–160.
Carlier, G., and R.A. Dana. 2008. Two-persons efficient risk-sharing and equilibria for concave law-invariant utilities. Economic Theory 36 (2): 189–223.
Chakravarty, S., and D. Kelsey. 2015. Sharing ambiguous risks. Journal of Mathematical Economics 56: 1–8.
Chateauneuf, A., M. Cohen, and I. Meilijson. 2004. Four notions of mean-preserving increase in risk, risk attitudes and applications to the rank-dependent expected utility model. Journal of Mathematical Economics 40 (5): 547–571.
Chateauneuf, A., R.-A. Dana, and J.-M. Tallon. 2000. Optimal risk-sharing rules and equilibria with Choquet-expected-utility. Journal of Mathematical Economics 34 (2): 191–214.
Chiu, W.H. 2012. Risk aversion, downside risk aversion and paying for stochastic improvements. The Geneva Risk and Insurance Review 37 (1): 1–26.
Chiu, W.H., L. Eeckhoudt, and B. Rey. 2012. On relative and partial risk attitudes: Theory and implications. Economic Theory 50 (1): 151–167.
Chung, H.-K., P. Glimcher, and A. Tymula. 2019. An experimental comparison of risky and riskless choice-limitations of prospect theory and expected utility theory. American Economic Journal: Microeconomics 11 (3): 34–67.
Clarke, D.J. 2016. A theory of rational demand for index insurance. American Economic Journal: Microeconomics 8 (1): 283–306.
Cole, S., X. Giné, J. Tobacman, P. Topalova, R. Townsend, and J. Vickery. 2013. Barriers to household risk management: Evidence from India. American Economic Journal: Applied Economics 5 (1): 104–135.
Collier, B., D. Schwartz, H. Kunreuther, and E. Michel-Kerjan. 2021. Insuring large stakes: A normative and descriptive analysis of households’ flood insurance coverage. The Journal of Risk and Insurance. https://doi.org/10.1111/jori.12363.
Cummins, D., and O. Mahul. 2003. Optimal insurance with divergent beliefs about insurer total default risk. Journal of Risk and Uncertainty 27 (2): 121–138.
Diecidue, E., and P. Wakker. 2002. Dutch books: Avoiding strategic and dynamic complications, and a comonotonic extension. Mathematical Social Sciences 43 (2): 135–149.
Dionne, G., and J. Li. 2014. When can expected utility handle first-order risk aversion? Journal of Economic Theory 154: 403–422.
Doherty, N.A., and L. Eeckhoudt. 1995. Optimal insurance without expected utility: The dual theory and the linearity of insurance contracts. Journal of Risk and Uncertainty 10 (2): 157–179.
Doherty, N.A., and H. Schlesinger. 1990. Rational insurance purchasing: Consideration of contract nonperformance. The Quarterly Journal of Economics 105 (1): 243–253.
Epper, T., and H. Fehr-Duda. 2017. A tale of two tails: On the coexistence of overweighting and underweighting of rare extreme events. Working Paper No. 1705 (University of St. Gallen Working Paper Series).
Etchart-Vincent, N. 2004. Is probability weighting sensitive to the magnitude of consequences? An experimental investigation on losses. Journal of Risk and Uncertainty 28 (3): 217–235.
Fox, C., B. Rogers, and A. Tversky. 1996. Options traders exhibit subadditive decision weights. Journal of Risk and Uncertainty 13 (1): 5–17.
Friedl, A., K.L. De Miranda, and U. Schmidt. 2014. Insurance demand and social comparison: An experimental analysis. Journal of Risk and Uncertainty 48 (2): 97–109.
Ghossoub, M. 2019. Optimal insurance under rank-dependent expected utility. Insurance: Mathematics and Economics 87: 51–66.
Ghossoub, M., and X.D. He. 2020. Comparative risk aversion in RDEU with applications to optimal underwriting of securities issuance. Insurance: Mathematics and Economics 101: 6–22.
Goldstein, W.M., and H.J. Einhorn. 1987. Expression theory and the preference reversal phenomena. Psychological Review 94 (2): 236–254.
Hansen, J.V., R.H. Jacobsen, and M.I. Lau. 2016. Willingness to pay for insurance in Denmark. The Journal of Risk and Insurance 83 (1): 49–76.
Harbaugh, W.T., K. Krause, and L. Vesterlund. 2010. The fourfold pattern of risk attitudes in choice and pricing tasks. The Economic Journal 120 (545): 595–611.
Harrison, G.W., and J.M. Ng. 2018. Welfare effects of insurance contract non-performance. The Geneva Risk and Insurance Review 43 (1): 39–76.
Hertwig, R., G. Barron, E.U. Weber, and I. Erev. 2004. Decisions from experience and the effect of rare events in risky choice. Psychological Science 15 (8): 534–539.
Hertwig, R., and I. Erev. 2009. The description-experience gap in risky choice. Trends in Cognitive Sciences 13 (12): 517–523.
Hong, C.S., E. Karni, and Z. Safra. 1987. Risk aversion in the theory of expected utility with rank dependent probabilities. Journal of Economic Theory 42 (2): 370–381.
Huang, R.J., P.-T. Shih, and L.Y. Tzeng. 2012. Disappointment and the optimal insurance contract. The Geneva Risk and Insurance Review 37 (2): 258–284.
Jaspersen, J.G., M. Ragin, and J. Sydnor. 2021. Predicting insurance demand from risk attitudes. The Journal of Risk and Insurance, 1– 34. https://doi.org/10.1111/jori.12342.
Jaspersen, J.G. 2016. Hypothetical surveys and experimental studies of insurance demand: A review. The Journal of Risk and Insurance 83 (1): 217–255.
Jewitt, I. 1989. Choosing between risky prospects: The characterization of comparative statics results, and location independent risk. Management Science 35 (1): 60–70.
Jindal, P. 2014. Risk preferences and demand drivers of extended warranties. Marketing Science 34 (1): 39–58.
Kahneman, D., and A. Tversky. 1979. Prospect theory: An analysis of decision under risk. Econometrica 47 (2): 263–291.
Kőszegi, B., and M. Rabin. 2007. Reference-dependent risk attitudes. The American Economic Review 97 (4): 1047–1073.
Krawczyk, M.W., S.T. Trautmann, and G. van de Kuilen. 2017. Catastrophic risk: Social influences on insurance decisions. Theory and Decision 82 (3): 309–326.
Lambregts, T., P. van Bruggen, and H. Bleichrodt. 2021. Insurance decisions under nonperformance risk and ambiguity. Journal of Risk and Uncertainty. https://doi.org/10.1007/s11166-021-09364-7.
Laury, S.K., M.M. McInnes, and J.T. Swarthout. 2009. Insurance decisions for low probability losses. Journal of Risk and Uncertainty 39 (1): 17–44.
Li, H., S. Neumuller, and C. Rothschild. 2021. Optimal annuitization with imperfect information about insolvency risk. The Journal of Risk and Insurance 88: 101–130.
Li, L., and R. Peter. 2021. Should we do more when we know less? The effect of technology risk on optimal effort. The Journal of Risk and Insurance. https://doi.org/10.1111/jori.12339.
Machina, M.J. 1995. Non-expected utility and the robustness of the classical insurance paradigm. The Geneva Papers on Risk and Insurance Theory 20 (1): 9–50.
Mahul, O., and B. Wright. 2007. Optimal coverage for incompletely reliable insurance. Economics Letters 95 (3): 456–461.
McIntosh, C., F. Povel, and E. Sadoulet. 2019. Utility, risk and demand for incomplete insurance: Lab experiments with Guatemalan co-operatives. The Economic Journal 129 (622): 2581–2607.
Menegatti, M., and R. Peter. 2021. Changes in risky benefits and in risky costs: A question of the right order. Management Science. https://doi.org/10.1287/mnsc.2021.4081.
Meyer, J., and M.B. Ormiston. 1999. Analyzing the demand for deductible insurance. Journal of Risk and Uncertainty 18 (3): 223–230.
Mossin, J. 1968. Aspects of rational insurance purchasing. Journal of Political Economy 76 (4): 553–568.
NAIC. 2017. Property-Casualty Insurer Financial Statement Filings 1997-2017. National Association of Insurance Commissioners.
Peter, R., and J. Ying. 2020. Do you trust your insurer? Ambiguity about contract nonperformance and optimal insurance demand. Journal of Economic Behavior & Organization 180: 938–954.
Pratt, J. 1964. Risk aversion in the small and in the large. Econometrica 32 (1): 122–136.
Prelec, D. 1998. The probability weighting function. Econometrica 66 (3): 497–527.
Quiggin, J. 1982. A theory of anticipated utility. Journal of Economic Behavior & Organization 3 (4): 323–343.
Quiggin, J. 1993. Generalized expected utility theory: The rank dependent model. New York: Springer.
Rabin, M. 2000. Risk aversion and expected-utility theory: A calibration theorem. Econometrica 68 (5): 1281–1292.
Rothschild, M., and J. Stiglitz. 1970. Increasing risk I. A definition. Journal of Economic Theory 2 (3): 225–243.
Ryan, M.J. 2006. Risk aversion in RDEU. Journal of Mathematical Economics 42 (6): 675–697.
Sarin, R., and P. Wakker. 1998. Revealed likelihood and Knightian uncertainty. Journal of Risk and Uncertainty 16 (3): 223–250.
Schlesinger, H. 1981. The optimal level of deductibility in insurance contracts. The Journal of Risk and Insurance 48 (3): 465–481.
Schlesinger, H. 1993. Risk management decisions when effectiveness is unreliable. In Workers’ Compensation Insurance: Claim Costs, Prices, and Regulation, pp. 307–328. Springer.
Schlesinger, H. 1997. Insurance demand without the expected-utility paradigm. The Journal of Risk and Insurance 64 (1): 19–39.
Schlesinger, H. 2013. The theory of insurance demand. In Handbook of Insurance, ed. G. Dionne, 167–184. Springer.
Schlesinger, H., and J.-M.G. von der Schulenburg. 1987. Risk aversion and the purchase of risky insurance. Journal of Economics (Zeitschrift für Nationalökonomie) 47 (3): 309–314.
Schmeidler, D. 1989. Subjective probability and expected utility without additivity. Econometrica 57 (3): 571–587.
Schmidt, U. 1998. Axiomatic utility theory under risk: Non-archimedean representations and application to insurance economics, vol. 461. New York: Springer.
Schmidt, U. 1999. Efficient risk-sharing and the dual theory of choice under risk. The Journal of Risk and Insurance 66 (4): 597–608.
Schmidt, U. 2016. Insurance demand under prospect theory: A graphical analysis. The Journal of Risk and Insurance 83 (1): 77–89.
Schmidt, U., C. Starmer, and R. Sugden. 2008. Third-generation prospect theory. Journal of Risk and Uncertainty 36 (3): 203–223.
Segal, U. 1988. Probabilistic insurance and anticipated utility. The Journal of Risk and Insurance 55 (2): 287–297.
Segal, U. 1990. Two-stage lotteries without the reduction axiom. Econometrica 58 (2): 349–377.
Segal, U., and A. Spivak. 1990. First order versus second order risk aversion. Journal of Economic Theory 51 (1): 111–125.
Selten, R., A. Sadrieh, and K. Abbink. 1999. Money does not induce risk neutral behavior, but binary lotteries do even worse. Theory and Decision 46 (3): 213–252.
Shapira, Z., and I. Venezia. 2008. On the preference for full-coverage policies: Why do people buy too much insurance? Journal of Economic Psychology 29 (5): 747–761.
Slovic, P., B. Fischhoff, S. Lichtenstein, B. Corrigan, and B. Combs. 1977. Preference for insuring against probable small losses: Insurance implications. The Journal of Risk and Insurance 44 (2): 237–258.
Snow, A. 2011. Ambiguity aversion and the propensities for self-insurance and self-protection. Journal of Risk and Uncertainty 42 (1): 27–43.
Stott, H. 2006. Cumulative prospect theory’s functional menagerie. Journal of Risk and Uncertainty 32 (2): 101–130.
Sydnor, J.R. 2010. (Over)insuring modest risks. American Economic Journal: Applied Economics 2 (4): 177–199.
Tsanakas, A., and N. Christofides. 2006. Risk exchange with distorted probabilities. ASTIN Bulletin 36 (1): 219–243.
Tversky, A., and D. Kahneman. 1992. Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty 5 (4): 297–323.
Tversky, A., and P. Wakker. 1995. Risk attitudes and decision weights. Econometrica 63 (6): 1255–1280.
Von Peter, G., S. Von Dahlen, and S.C. Saxena. 2012. Unmitigated disasters? New evidence on the macroeconomic cost of natural catastrophes. BIS Working Paper No 394.
Wakker, P. 2010. Prospect theory: For risk and ambiguity. Cambridge: Cambridge University Press.
Wakker, P., R.H. Thaler, and A. Tversky. 1997. Probabilistic insurance. Journal of Risk and Uncertainty 15 (1): 7–28.
Wu, G., and R. Gonzalez. 1996. Curvature of the probability weighting function. Management Science 42 (12): 1676–1690.
Xia, J., and X.Y. Zhou. 2016. Arrow-Debreu equilibria for rank-dependent utilities. Mathematical Finance 26 (3): 558–588.
Xu, Z.Q., X.Y. Zhou, and S.C. Zhuang. 2019. Optimal insurance under rank-dependent utility and incentive compatibility. Mathematical Finance 29 (2): 659–692.
Yaari, M.E. 1987. The dual theory of choice under risk. Econometrica 55: 95–115.
Zimmer, A., H. Gründl, C.D. Schade, and F. Glenzer. 2018. An incentive-compatible experiment on probabilistic insurance and implications for an insurer’s solvency level. The Journal of Risk and Insurance 85 (1): 245–273.
Zimmer, A., C. Schade, and H. Gründl. 2009. Is default risk acceptable when purchasing insurance? Experimental evidence for different probability representations, reasons for default, and framings. Journal of Economic Psychology 30 (1): 11–23.
Acknowledgements
Financial support by the Deutscher Verein für Versicherungswissenschaft e.V. is greatly appreciated. We are indebted to Markus Fels, Tobias Huber, Ulrich Schmidt, Justin Sydnor, Ruojin Zhang, and seminar participants at Universität Innsbruck, University of Guelph, University of Wisconsin-Madison, Temple University, the 2018 American Risk and Insurance Association Annual Meeting, the 2018 European Group of Insurance Economists Annual Seminar, and the 2019 CEAR/MRIC Behavioral Insurance Workshop for helpful comments. We also thank two anonymous referees and the editor Alexander Mürmann for a constructive review process, which stimulated additional results and helped us improve the presentation of the paper.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Supplementary Information
Below is the link to the electronic supplementary material.
Appendices
Appendix A: Probability weighting functions and DRO
1.1 A.1 Common parametric classes of probability weighting functions
We use several classes of probability weighting functions to illustrate our results. We introduce them here for reference and note some of their features.Footnote 21 Many probability weighting functions have initially been developed for gain lotteries, and while differences between gain and loss domain estimates tend to be small (Tversky and Kahneman 1992), they do exist (Etchart-Vincent 2004). We start with the probability weighting function introduced by Goldstein and Einhorn (GE, 1987):
with \(r , s > 0\) to ensure monotonicity. Examples are shown in Panel (a) of Fig. 4. The GE probability weighting function can be S-shaped (\(r>1\)), inverse S-shaped (\(r<1\)), concave (\(r=1, s>1\)) or convex (\(r=1, s<1\)), and the identity is obtained for \(r=s=1\). Parameter r mostly controls curvature, while s steers elevation.
The functional form proposed for Prospect Theory’s rank-dependent version, Cumulative Prospect Theory (CPT), was introduced by Tversky and Kahneman (TK, 1992 Panel (b) of Fig. 4):
with \(r > 0.2793\) for monotonicity. It is inverse S-shaped for \(r<1\), reverts to the identity for \(r=1\), and is S-shaped for \(1<r \le 2\).Footnote 22 Parameter r controls both curvature and elevation, but in opposite directions. A two-parameter version of the TK function was initially proposed by Wu and Gonzalez (WG, 1996) and is given by
with \(r, s > 0\).Footnote 23 As can be seen in Panel (c) of Fig. 4, s controls elevation while r is inversely related to curvature. The function \(w^{WG}\) is inverse S-shaped for \(r < 1\), contains the identity as a special case for \(r =1\), and is S-shaped for \(r >1\) as long as \(s > (r-1)/r\).Footnote 24
Prelec (1998) derives two probability weighting functions axiomatically. The one-parameter version (Prl-I) is given by
with \(r>0\) for monotonicity. We obtain an inverse S-shape for \(r<1\) (see Panel (d) of Fig. 4), the identity for \(r=1\), and an S-shape for \(r>1\). This class of probability weighting functions intersects the identity at its inflection point at \({\widetilde{p}} = p^* = 1/e\). It has fixed elevation and its curvature is inversely related to r. The two-parameter version (Prl-II, see Panel (e) of Fig. 4) is
and \(r, s > 0\) guarantee monotonicity. This class of probability weighting functions control elevation via s, exhibit an inverse S-shape for \(r <1\) and an S-shape for \(r >1\). For \(r =1\), it nests the class of power weighting functions \(w^{Pwr}(p) = p^s\) (not illustrated), which are either convex for \(s > 1\), concave for \(s<1\), or revert to the identity for \(s = 1\).
Another relevant class of probability weighting functions, which has received praise for its empirical appeal (see Wakker 2010), is the neo-additive class,
with parameters \(r \in (0,1)\) and \(s \in (-r, r)\). They are straight lines that are flatter than the identity and have discontinuities at both ends of the unit interval. Parameter r inversely measures slope and s controls elevation. We illustrate this class in Panel (f) of Fig. 4.
1.2 Decreasing relative overweighting
The DRO region plays an important role in our comparative static analysis. We will now derive the DRO region for various classes of probability weighting functions. Any inverse S-shaped probability weighting function with fixed point \(p^*\) and inflection point \({\widetilde{p}}\) has two points \(p'\) and \(p''\), one smaller and one larger than \(p^*\) and \({\widetilde{p}}\), which define the likelihood insensitivity region. For \(p \in (p', p'')\) the probability weighting function is flatter than the identity, \(w'(p) < 1\), while it is steeper than the identity on \((0,p') \cup (p'',1)\), see Lemma 1 in Baillon et al. (2020). Likewise, any S-shaped probability weighting function has two points \(p'\) and \(p''\) such that \(w'(p) > 1\) for \(p \in (p', p'')\) and \(w'(p) < 1\) for \(p \in (0,p') \cup (p'',1)\). We will first establish some general results about DRO regions for probability weighting functions with no more than one change in curvature (inverse S-shaped, S-shaped, concave, convex, neo-additive), and then apply them to specific parametric classes.
Proposition 7
Consider a probability weighting function w that is twice continuously differentiable on (0, 1) with no more than one inflection point.
-
(i)
If w is inverse S-shaped, the DRO region is \((0,{\hat{p}})\) for a \({\hat{p}} \in (\max (p^*,{\widetilde{p}}),p'')\).
-
(ii)
If w is S-shaped, the DRO region is \(({\hat{p}},1]\) for a \({\hat{p}} \in (\max (p^*,{\widetilde{p}}),p'')\).
-
(iii)
If w is concave or neo-additive, the DRO region is (0, 1]; if w is convex, the DRO region is empty.
For parametric probability weighting functions, we obtain \({\hat{p}}\) as follows:
-
(iv)
\({\hat{p}}^{GE}\) is implicitly defined via \(\frac{r}{1-{\hat{p}}^{GE}} - s \left( \frac{{\hat{p}}^{GE}}{1-{\hat{p}}^{GE}}\right) ^r = 1\).
-
(v)
\({\hat{p}}^{TK}\) is implicitly defined via \((r-1) \left( \frac{1-{\hat{p}}^{TK}}{{\hat{p}}^{TK}}\right) ^{r} + \left( \frac{1-{\hat{p}}^{TK}}{{\hat{p}}^{TK}}\right) ^{r-1} = 2-r\).
-
(vi)
\({\hat{p}}^{WG}\) is implicitly defined via \((r-1) \left( \frac{1-{\hat{p}}^{WG}}{{\hat{p}}^{WG}} \right) ^{r} + r s \left( \frac{1-{\hat{p}}^{WG}}{{\hat{p}}^{WG}} \right) ^{r-1} = 1+r(s-1)\).
-
(vii)
\({\hat{p}}^{Prl-I} = \exp \left( -r^{\frac{1}{1-r}} \right)\) and \({\hat{p}}^{Prl-II} = \exp \left( -(r s)^{\frac{1}{1-r}} \right)\).
Proof
-
(i) By definition, \(\rho (p) = (w(p)-p)/p\) with derivative \(\rho '(p) = (pw'(p)-w(p))/p^2\). We denote the numerator of \(\rho '\) by g. DRO holds whenever g is negative. Using the properties of inverse S-shaped probability weighting functions, we find that \(\lim _{p \rightarrow 0} g(p) = 0\), \(\lim _{p \rightarrow 1} g(p) > 0\) and \(g'(p) = pw''(p)\) for \(p \in (0,1)\). Therefore, g is strictly decreasing for \(p \in (0,{\widetilde{p}})\), reaches a global minimum at \(p={\widetilde{p}}\), and is strictly increasing for \(p \in ({\widetilde{p}},1)\). This shows the existence of a unique zero of g between \({\widetilde{p}}\) and 1, denoted by \({\hat{p}}\), and g is negative for all \(p \in (0,{\hat{p}})\). Due to \(g(p^*) = p^*(w'(p^*)-1)<0\) and \(g(p'')=p''-w(p'')>0\), \({\hat{p}}\) must lie between \(p^*\) and \(p''\).
-
(ii) Follows with a similar argument. For S-shaped probability weighting functions, \(g(0) = 0\), \(g(1) = w'(1)-1<0\), and \(g'\) is strictly increasing for \(p \in (0,{\widetilde{p}})\), has a global maximum at \(p={\widetilde{p}}\), and is strictly decreasing for \(p \in ({\widetilde{p}},1)\). This proves the existence and uniqueness of \({\hat{p}}\). Furthermore, \(g(p^*) > 0\) and \(g(p'')<0\) so that \({\hat{p}}\) must lie between \(p^*\) and \(p''\).
-
(iii) For concave probability weighting functions, \(\lim _{p \rightarrow 0} g(p) = 0\), \(g(1)<0\) and \(g'(p)<0\) on (0, 1] so that g is negative on (0, 1]. For convex probability weighting functions, \(g(0)=0\), \(\lim _{p \rightarrow 1} g(p)>0\) and \(g'(p)>0\) on (0, 1] so that g is positive on (0, 1]. For the neo-additive class we obtain \(g(p) = (r-s)/2\), which is negative on (0, 1).
-
(iv) to (vii) follow per direct computation by rearranging \(g({\hat{p}}) = 0\).
\(\square\)
DRO regions of inverse S-shaped probability weighting functions include all overweighted probabilities, all probabilities where w is concave, and some probabilities that are underweighted and where concavity does not hold. DRO regions can be quite large. For example, \({\hat{p}}^{Prl-I}\) is negatively associated with r and \(\lim _{r \rightarrow 1} {\hat{p}}^{Prl-I} = \exp (-1/e) \approx 0.6922\). When the Prelec-I function is inverse S-shaped (i.e., for \(r <1\)), the DRO region includes at least all probabilities below \(69.22\%\), and even larger probabilities the smaller the value of parameter r. A similar argument shows that the lowest \({\hat{p}}^{TK}\) for inverse S-shaped TK weighting functions is 0.75 so that DRO regions in this case include at least all probabilities up to \(75\%\), and contain probabilities above \(75\%\) for values of r below 1. Both of the upper bounds are in a region where probabilities are underweighted.
This suggests that our focus on loss probabilities in the DRO region is a mild assumption. Figure 5 plots \({\hat{p}}\) for various parameter values of inverse S-shaped probability weighting functions. With sufficient elevation (high s in GE or low s in WG and Prl-II), the DRO region is large. For almost all r and s parameter values reported in the literature (see Table 5 in Stott 2006), nearly all loss probabilities relevant in insurance lie in the DRO region, the main exception being maybe the probability to claim on a health insurance policy (e.g., Bhargava et al. 2017).
Based on our own experimental data (see Section 5), we calibrate the different classes of probability weighting functions and calculate the upper bound \({\hat{p}}\) of the DRO region for each subject under the given function. Table 4 summarizes the distribution of \({\hat{p}}\) for subjects exhibiting inverse S-shaped probability weighting. Even the lowest 10th percentile of the distribution for \({\hat{p}}\) still leads to a DRO region that is large enough to contain all loss probabilities relevant in insurance demand.
Appendix B: Mathematical proofs
1.1 Determining the Loading Thresholds in Equation (7)
The first-order condition for objective function (3) is
where \(x_1^*\) and \(x_2^*\) denote final wealth in the no-loss and the loss state at the optimal level of insurance demand \(\alpha ^*_W\). The second-order condition is satisfied because the objective function is globally concave in \(\alpha\) due to \(u''<0\). The first-order expression is then strictly decreasing in \(\alpha\). We derive the full-insurance bound and the no-insurance bound by solving \(\left. \partial W/\partial \alpha \right| _{\alpha =1} \ge 0\) and \(\left. \partial W/\partial \alpha \right| _{\alpha =0} \le 0\) for m. This yields Equation (7). Diminishing marginal utility implies \({\underline{m}}_W<{\overline{m}}_W\).
1.2 Proof of Proposition 1 and Additional Comparative Statics
The full-insurance bound \({\underline{m}}_W\) can be rewritten as \(1+\delta (p)/p\), which is increasing in the absolute amount of overweighting. We rearrange the no-insurance bound as follows:
Therefore, \({\overline{m}}_W\) increases in the absolute amount of overweighting. This shows result 1(i).
For 1(ii), we need to compare insurance demand under EU and under RDU. When the individual overweights the loss probability, we know from 1(i) that \({\underline{m}}_U < {\underline{m}}_W\) and \({\overline{m}}_U < {\overline{m}}_W\). We distinguish different cases for the loading factor. If \(m \le {\underline{m}}_U\), full coverage is optimal under EU and under RDU. If \({\underline{m}}_U < m \le {\underline{m}}_W\), less than full coverage is optimal under EU, whereas full coverage is optimal under RDU. If \(m \in ({\underline{m}}_W, {\overline{m}}_U)\),Footnote 25 partial insurance is optimal under EU and under RDU but insurance demand is higher under RDU because
If \({\overline{m}}_U \le m < {\overline{m}}_W\), no insurance is optimal under EU but partial insurance is optimal under RDU. For \(m \ge {\overline{m}}_W\) no insurance is optimal under both EU and RDU. So the individual always purchases at least as much insurance under RDU as under EU, and strictly more for \(m \in ({\underline{m}}_U, {\overline{m}}_W)\). The reasoning for underweighting is analogous.
To show results 1(iii) and 1(iv), we first provide comparative statics with respect to the loss probability p. We rewrite the full-insurance bound as \({\underline{m}}_W = 1 + \rho (p)\), which is decreasing in p for loss probabilities in the DRO region. For the effect on \({\overline{m}}_W\), consider the numerator of \({\partial {\overline{m}}_W} / {\partial p}\), which after some rearrangement is given by
The first square bracket is negative because DRO at p is equivalent to the probability weighting function being elastic at p. The second square bracket is negative due to diminishing marginal utility. Hence, an increase in the loss probability increases \({\overline{m}}_W\). The ratio \({\overline{m}}_W / {\underline{m}}_W\) is decreasing in p, regardless of whether p is in the DRO region or not, because
An increase in p raises w(p), which increases the denominator so that \({\overline{m}}_W / {\underline{m}}_W\) decreases. If p is in the DRO region, the range of loadings where partial insurance is optimal decreases in p. This follows from \({{\overline{m}}_W} - {{\underline{m}}_W} = {{\underline{m}}_W} \cdot \big [{\overline{m}}_W / {\underline{m}}_W - 1 \big ]\) because both factors are decreasing in p.
These results imply that \({\underline{m}}_W / {\underline{m}}_U\) is decreasing in p for p in the DRO region because \({\underline{m}}_U=1\) and \({\underline{m}}_W\) is decreasing in p under DRO. This shows (iii). For (iv), we compute
Taking the derivative of \({\overline{m}}_W / {\overline{m}}_U\) with respect to p and rearranging its numerator yields:
For p in the DRO region, the square bracket is less than \(w(p)(w(p)-p)(u'(x)-u'(x-L))\), which is negative for \(w(p)>p\). Then, a lower loss probability raises \({\overline{m}}_W / {\overline{m}}_U\).
1.3 Proof of Proposition 2
We rewrite the first-order condition (B.1) for an interior solution as follows:
We can then solve for \(\alpha ^*_W\) when the utility function is exponential or iso-elastic. For exponential utility, we have \(u(x) = (1-e^{-Ax})/A\) with \(A>0\), and optimal insurance demand is given by
Solving for utility curvature A yields
with the following derivatives:
For iso-elastic utility, we have \(u'(x) = x^{-\gamma }\) with \(\gamma > 0\). Optimal insurance demand is then given as follows:
Solving for the utility curvature parameter \(\gamma\) renders
This differs from (B.10) only by a non-negative factor that does not depend on \(\delta (p)\). Therefore, \(\mathrm {d}\gamma /\mathrm {d}\delta (p)\) and \(\mathrm {d}^2\gamma /\mathrm {d}\delta (p)^2\) have the same sign as for exponential utility. This proves 2(i).
For 2(ii), note that \(\mathrm {d}A / \mathrm {d}\delta (p)\) is more negative the higher \(\alpha _W^*\), the lower p as long as \(w(p) < 0.5\), and the lower L. When \(\mathrm {d}^2A / \mathrm {d}\delta (p)^2\) is positive, it is more positive the higher \(\alpha _W^*\), the lower p, and the lower L. For exponential utility, this is directly evident from Equations (B.11) and (B.12). For iso-elastic utility, \(\ln \left( x_1^*/x_2^*\right)\) is decreasing in \(\alpha _W^*\), increasing in p, and increasing in L, so 2(ii) follows from (B.11) and (B.12) with a similar argument.
1.4 Proof of Proposition 3
After some rearrangements and simplifications, the first-order condition for objective function (9) is given as follows:
For \(D=0\), we obtain \(P(0) = mp \int _0^L \ell \, \mathrm {d}F(\ell )\) for the premium and hence
This is nonpositive for \(m \le w(p)/p\), indicating that raising the deductible above zero would lower the value of the objective function. Hence, full insurance is optimal. For no insurance, we set \(D=L\) and obtain \(P(L) = 0\). Notice that
because \(F(L) = 1\) and \(w(0)=0\). Rewrite the first-order expression as follows:
When \(m > {\overline{m}}_W\), the square bracket is strictly positive for \(D=L\). Due to continuity, it remains positive for values of D slightly below L, indicating that the value of the objective function can be increased by raising the deductible. This establishes that no insurance is optimal, \(D^*_W = L\). On the flip side, when \(m < {\overline{m}}_W\), the square bracket is strictly negative for \(D=L\). Due to continuity, it remains negative for values of D slightly below L, and the objective function can be increased by lowering the deductible. Therefore, some insurance is optimal, \(D^*_W<L\). Again by continuity, this implies that \(D^*_W = L\) for \(m={\overline{m}}_W\) because otherwise the optimal deductible level would exhibit a jump at \(m={\overline{m}}_W\).
Given that the full-insurance bound is the same as in the coinsurance problem, result 3(i) follows immediately. For result 3(ii), \(\lim _{p \rightarrow 0} w'(p) = \infty\) implies \({\overline{m}}_W = \infty\), which exceeds \({\overline{m}}_U\). When \(w'(0) < \infty\), we obtain that \({\overline{m}}_W \ge {\overline{m}}_U\) if and only if
Overweighting of the loss probability and concavity of the probability weighting function on (0, p] imply that \(w'(0) > 1\).Footnote 26 This together with overweighting of p implies that the first square bracket is positive. The second square bracket is non-negative because \(p(1-F(\ell ))\) is in the concave portion of w so that \(w'(p(1-F(\ell ))) \le w'(0)\) for all \(\ell \in [0,L]\).
For result 3(iii), we first characterize the optimal deductible \(D^*_U\) under EU via the corresponding first-order condition, which is given by
When inserting \(D^*_U\) into the first-order expression under RDU, we can utilize the above condition and obtain the following:
The first square bracket is negative if and only if
Overweighting of p and concavity up to p of the probability weighting function imply that (0, p] is part of the DRO region. In this case, the left-hand side of (B.22) exceeds w(p)/p, which exceeds the right-hand side of (B.22) because p is overweighted. The second square bracket in (B.21) is also negative because the probability weighting function is concave on (0, p]. As a result, we obtain that
This indicates that probability weighting induces the individual to lower the optimal deductible, which is equivalent to higher insurance demand in the deductible choice problem.
1.5 Proof of Proposition 4
We fix the expected loss by setting \(pL = const\). Then, \((\mathrm {d}p/\mathrm {d}p) \cdot L + p \cdot (\mathrm {d}L/\mathrm {d}p) = 0\) so that \(\mathrm {d}L/\mathrm {d}p = -L/p\). By rewriting \({\underline{m}}_W\) as \(1+\rho (p)\), we can see that \({\underline{m}}_W\) increases following a mean-preserving spread of the insured risk as long as the loss probability remains in the DRO region. Under the binary risk assumption, a mean-preserving spread reduces p and simultaneously increases L. We calculate this derivative explicitly,
and find that DRO at p is equivalent to \(p w'(p) < w(p)\).
We then take the derivative of \({\overline{m}}_W\) with respect to p while using \(\mathrm {d}L/\mathrm {d}p = -L/p\). After some simplifications, the numerator is given by:
The first term is negative due to \(u''<0\). The sign of the second term depends on the square bracket, which is negative if \(p w'(p) < w(p)\). So for loss probabilities in the DRO region, \({\overline{m}}_W\) increases after a mean-preserving spread of the insured risk.
For optimal insurance demand \(\alpha ^*_W \in (0,1)\), recall first-order condition (B.1). The implicit function theorem and the concavity of the objective function imply that the sign of \(\left. \partial \alpha ^*_W/\partial p \right| _{pL=const}\) coincides with the sign of \(\left. \partial ^2 W/\partial \alpha \partial p \right| _{pL = const}\). This cross-derivative is given by:
The five terms represent different economic effects on insurance demand when the insured risk becomes riskier.Footnote 27 To determine the net effect, we solve for \(u'(x_1^*)\) from the first-order condition,
substitute, rearrange and combine terms to obtain:
The second term is negative because \(u''<0\). The first term is negative if DRO holds at p. To see this, recall that an interior solution requires \(m > {\underline{m}}_W = w(p)/p\). The square bracket in (B.28) is then no larger than
This is negative for p in the DRO region. Hence, optimal insurance demand increases following a mean-preserving spread of the insured risk because such a change lowers p.
1.6 Proof of Proposition 5
The first-order condition associated with (14) is given by
The threshold \({\underline{m}}_W\) is implicitly defined via \(\left. \partial W_{NP}/\partial \alpha \right| _{\alpha = 1} = 0\). To determine the effect of nonperformance risk at the margin, we interpret \(\left. \partial W_{NP}/\partial \alpha \right| _{\alpha = 1}\) as a function of m and q, apply the implicit function theorem to obtain \(\mathrm {d} m/\mathrm {d}q\), and evaluate it at \(q=1\). Define
then
and
because \(\pi _3 = 0\) and \(m = {\underline{m}}_W\) for \(q=1\). We know from Equation (7) that \({\underline{m}}_W = w(p)/p\), so the second and third term in \(\left. \partial {\underline{F}}/\partial m \right| _{q=1}\) cancel each other out. Hence,
Furthermore,
so that
because \(\pi _3 = 0\) and \(m = {\underline{m}}_W\) when \(q=1\). If \(\lim _{p \rightarrow 0} w'(p) = \infty\), which is the case for many parametric inverse S-shaped probability weighting functions, then \(\lim _{q \rightarrow 1} \partial {\underline{F}}/\partial q = \infty\). If \(w'(0)\) is finite, we use the fact that \({\underline{m}}_W = w(p)/p\) to simplify the last expression as follows:
Hence,
The first round bracket is positive due to diminishing marginal utility; the second round bracket is positive because the DRO region contains (0, p] so that \(w(\varepsilon )/\varepsilon\) is decreasing for \(\varepsilon \le p\) and \(w'(0) = \lim _{\varepsilon \rightarrow 0} w(\varepsilon )/\varepsilon\). Also, \(\lim _{q \rightarrow 1} \mathrm {d} {\underline{m}}_W / \mathrm {d} q = \infty\) whenever \(\lim _{p \rightarrow 0} w'(p) = \infty\). In any case, starting at no nonperformance risk (\(q=1\)), any small decrease of q reduces \({\underline{m}}_W\).
The threshold \({\overline{m}}_W\) is implicitly defined via \(\left. \partial W_{NP} / \partial \alpha \right| _{\alpha = 0} = 0\). To determine the effect of nonperformance risk at the margin, we interpret \(\left. \partial W_{NP} / \partial \alpha \right| _{\alpha = 0}\) as a function of m and q, apply the implicit function theorem to obtain \(\mathrm {d} m / \mathrm {d}q\), and evaluate it at \(q=1\). Define
then direct computation shows that
For \(q=1\), we know from Equation (7) that
As a result,
which is infinite whenever \(\lim _{p \rightarrow 0} w'(p) = \infty\). If \(w'(0)\) is finite, the round bracket is positive because we assumed that (0, p] is part of the DRO region. Therefore, starting at no nonperformance risk (\(q=1\)), any small decrease of q reduces \({\overline{m}}_W\). This shows result 5(i).
To show result 5(ii), we need to determine the cross-derivative of \(W_{NP}\) with respect to \(\alpha\) and q and evaluate it at \(q=1\). This cross-derivative is given by
For \(q=1\), this expression simplifies to
The cross-derivative is infinite when \(\lim _{p \rightarrow 0} w'(p) = \infty\). If \(w'(0)\) is finite, we can use the first-order condition at \(q=1\), which is given by
and substitute it into \(\left. \partial ^2 W_{NP} / \partial \alpha \partial q \right| _{q=1}\). After some rearrangements, this yields the following:
The first square bracket is positive because the DRO region contains (0, p], the second square bracket is positive due to \(u''<0\), and the third square bracket is non-negative because of non-increasing absolute risk aversion. As a result, the cross-derivative is positive at \(q=1\), and potentially infinite, indicating that any small level of nonperformance risk reduces optimal insurance demand.
To prove result 5(iii), we need to assess the effect of probability weighting on optimal insurance demand at a given level of nonperformance risk. Let \(\alpha ^*_{U,NP}\) denote optimal insurance demand under EU. It is characterized by the following first-order condition:
Solving for \(u'(x_2^*)\) yields
When evaluating the individual’s first-order expression under RDU at \(\alpha ^*_{U,NP}\) and substituting condition (B.48), we obtain the following after some simplifications and rearrangements:
In the absence of nonperformance risk (i.e., for \(q=1\)), this simplifies to
which is positive because of \(w(p) > p\). Probability weighting increases insurance demand in the absence of nonperformance risk, as shown in Proposition 1(ii).
For the remainder of the proof, let \(q \in (0,1)\). Our assumptions ensure that (0, p] is part of the DRO region. Therefore, \(\delta (p(1-q))/p(1-q) > \delta (p)/p\), which is equivalent to \(\left[ pq\pi _3-p(1-q)\pi _2\right] >0\). We can then rearrange (B.49) as follows:
The sign coincides with the sign of the curly bracket. Nonperformance risk implies \(x_3^* < x_1^*\) so that \(u'(x_3^*)/u'(x_1^*)>1\) due to \(u''<0\). We denote the first fraction in the curly bracket by f(q) and examine its behavior on (0, 1) as a function of q. For \(q \rightarrow 1\), the numerator of f(q) converges to \((w(p)-p)\), which is positive because the loss probability is overweighted. The denominator of f(q) converges to 0 from above due to DRO so that \(\lim _{q \rightarrow 1} f(q) = \infty\). For \(q \rightarrow 0\), we obtain from L’Hôpital’s rule that
which may or may not exceed unity depending on whether the probability weighting function is steeper or flatter than the identity at the loss probability. For \(q \in (0,1)\), the derivative of f(q) with respect to q is given by
The numerator is non-negative because the loss probability is overweighted and the weighting function is assumed to be concave up to the loss probability p. Indeed, the curly bracket in (B.53) can be rearranged to
and concavity of w on (0, p] implies a positive sign. In conclusion, f is strictly increasing on (0, 1) with limits \(1+\frac{w'(p)-1}{w(p)-pw'(p)}\) for \(q \rightarrow 0\) and \(\infty\) for \(q \rightarrow 1\).
This renders two possibilities for how f(q) compares to \(u'(x_3^*)/u'(x_1^*)\). If \(1+\frac{w'(p)-1}{w(p)-pw'(p)} \ge u'(x_3^*)/u'(x_1^*)\), then f(q) exceeds \(u'(x_3^*)/u'(x_1^*)\) for any \(q \in (0,1)\). In this case, we set \({\hat{q}}=0\), and (B.51) is always positive implying higher insurance demand under RDU than under EU. On the other hand, f(q) can exceed \(u'(x_3^*)/u'(x_1^*)\) for some values of q and fall below it for others. Due to strict monotonicity and the limits, there will then be a unique \({\hat{q}} \in (0,1)\) separating high values of q from low values of q. Insurance demand under RDU is higher than under EU for \(q>{\hat{q}}\) and lower than under EU for \(q<{\hat{q}}\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jaspersen, J.G., Peter, R. & Ragin, M.A. Probability weighting and insurance demand in a unified framework. Geneva Risk Insur Rev 48, 63–109 (2023). https://doi.org/10.1057/s10713-022-00074-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1057/s10713-022-00074-x
Keywords
- Insurance demand
- Probability weighting
- Non-expected utility
- Comparative statics
- Decreasing relative overweighting