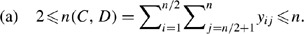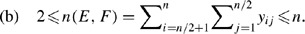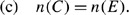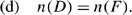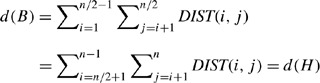Abstract
We describe the development of fast heuristics and methodologies for congestion minimization problems in directional wireless networks, and we compare their performance with optimal solutions. The focus is on the network layer topology control problem (NLTCP) defined by selecting an optimal ring topology as well as the flows on it. Solutions to NLTCP need to be computed in near realtime due to changing weather and other transient conditions and which generally preclude traditional optimization strategies. Using a mixed-integer linear programming formulation, we present both new constraints for this problem and fast heuristics to solve it. The new constraints are used to increase the lower bound from the linear programming relaxation and hence speed up the solution of the optimization problem by branch and bound. The upper and lower bounds for the optimal objective function to the mixed integer problem then serve to evaluate new node-swapping heuristics which we also present. Through a series of tests on different sized networks with different traffic demands, we show that our new heuristics achieve within about 0.5% of the optimal value within seconds.











Similar content being viewed by others
References
Banerjee D and Mukherjee B (1997). Wavelength routed optical networks: Linear formulation. Resource Budgeting Tradeoffs and Reconfiguration Study, IEEE INFOCOM 1997, Kobe, Japan, pp 269–276.
Conejo AJ, Castillo E, Minquez R and Garcia-Bertrand R (2006). Decomposition Techniques in Mathematical Programming. Engineering and Science Applications. Springer: Berlin.
Cosares S and Saniee I (1992). An optimization problem related to balancing loads on SONET rings. Technical Memorandum, Bellcore, Morristown, NJ, USA.
Costa AM (2005). A survey on Benders decomposition applied to fixed-charge network design problems. Comput Oper Res 32: 1429–1450.
Davis CC, Smolyaninov II and Milner SD (2003). Flexible optical wireless links and networks. IEEE Commun Magazine 41(3): 51–57.
Desai A and Milner S (2005). Autonomous reconfiguration in free space optical sensor networks. IEEE J Select Areas Commun 23: 1556–1563.
Desai A, Llorca J and Milner SD (2004). Autonomous reconfiguration of backbones in free space optical networks. Presented at the Military Communication Conference 2004, Monterey, CA.
Goldschmidt O, Laugier A and Olinick EV (2003). SONET/SDH ring assignment with capacity constraints. Disc Appl Math 129: 99–128.
Gutierrez GJ, Kouvelis P and Kurawarwala AA (1996). A robustness approach to uncapacitated network design problems. Eur J Oper Res 94: 362–376.
Ho TH, Trisno S, Smolyaninov II, Milner SD and Davis CC (2004). Studies of pointing, acquisition, and tracking of agile optical wireless transceivers for free-space optical communication networks. In: Gonglewski JD and Stein K (eds). in: Optics Atmospheric Propagation and Adaptive Systems VI, Proceedings of the SPIE, Vol. 5237. SPIE Digital Library, pp. 147–158.
Ho TH, Milner SD and Davis CC (2005). Fully optical real-time pointing, tracking and acquisition system for optical wireless link. In: Mecherle GS (ed). Photonics West, Proceedings of SPIE, Vol. 5712. SPIE Digital Library, pp 81–92.
Hoang HH (1982). Topological optimization of networks: A nonlinear mixed integer model employing generalized Benders decomposition. IEEE Trans Automat Control 27: 164–169.
Karunanithi N and Carpenter T (1994). A ring loading application of genetic algorithms. In: Proceedings of the 1994 ACM Symposium on Applied Computing, ACM: pp 227–231.
Kashyap A, Lee K and Shayman M (2003). Rollout algorithms for integrated topology control and routing in wireless optical backbone networks. Technical Report, TR 2003-51, Institute for Systems Research, University of Maryland.
Lee CY and Chang SG (1997). Balancing loads on SONET rings with integer demand splitting. Comput Oper Res 24: 221–229.
Lee K-I and Shayman M (2003). A local optimization algorithm for logical topology design and traffic grooming in IP over WDM Networks. Technical Research Report, TR 2003-3, Institute of Systems Research, University of Maryland, College Park.
Leonardi E, Mellia M and Marsan MA (2000). Algorithms for the logical topology design in WDM all-optical networks. Opt Network Mag 1: 35–46.
Llorca J Desai A, Vishkin U, Davis CC and Milner SD (2004). Reconfigurable optical wireless sensor networks, In: Gonglewski JD and Stein K (eds). Optics in Atmospheric Propagation and Adaptive Systems VI, Proceedings of the SPIE, Vol. 5237. SPIE Digital Library, pp 136–146.
Magnanti T, Mireault P and Wong RT (1986). Tailoring Benders decomposition for uncapacitated network design. Math Program Study 26: 112–154.
Milner SD, Desai A, Ho TH, Llorca J, Trisno S and Davis CC (2005). Self-organizing broadband hybrid wireless networks. J Opt Networks 4: 446–459.
Myung YS and Kim HG (2004). On the ring loading problem with demand splitting. Oper Res Lett 32: 167–173.
Myung YS, Kim HG and Tcha DW (1997). Optimal load balancing on SONET bidirectional rings. Oper Res 45: 148–152.
Papadimitriou CH and Steiglitz K (1982). Combinatorial Optimization: Algorithms and Complexity. Prentice-Hall Inc: Englewood Cliffs, New Jersey.
Ramaswamy R and Sivarajan K (1996). Design of logical topologies for wavelength routed optical networks. IEEE J Select Areas Commun 14: 840–851.
Schrijver A, Seymour P and Winkler P (1998). The ring loading problem. SIAM J Disc Math 11: 1–14.
van Hoesel SPM (2005). Optimization in telecommunication networks. Stat Neerl 59: 180–205.
Wang B-F (2005). Linear time algorithms for the ring loading problem with demand splitting. J Algorithms 54: 45–57.
Acknowledgements
This material is based upon work supported by the National Science Foundation under Grant No. CNS 04352060. We would like to thank Jifang Zhuang and Ruud Egging of the University of Maryland for their help on this paper.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Theorem 1
-
Consider a ring topology on n nodes. Then, each row or column of the distance matrix DIST defined by (14), will be a permutation of
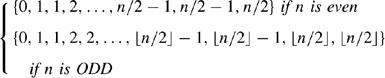
Proof
-
Pick an arbitrary node i. Since it is a ring topology, each of the other n−1 nodes are reachable from this node. In the clockwise direction, there is a node one arc away. Also, in the counter-clockwise direction there is a node one arc away. Continuing to count in the clockwise and then counter-clockwise direction, we see that there are nodes two arcs away, three arcs away and so on until the node furthest away from node i is reached. If n is even, there is one node furthest away, this node is n/2 arcs away in both the clockwise or counter-clockwise directions. If n is odd, then there are two nodes furthest away, at ⌊n/2⌋ arcs, one reachable in the clockwise and the other in the counter-clockwise direction. The result follows since the node i was arbitrary. □
Corollary 1
-
With either the row sum constraints or column sum constraints in force, no subtours are possible solutions to NLTCP.
Proof
-
If the row sum constraints are in force, then the sum of the elements for any row of the distance matrix is a specific finite number. But a subtour implies that there exists two nodes i and j that are not reachable by a series of arcs. Consequently, the distance between them is ∞. Thus, since distances are nonnegative, this would imply that for row i or j that the row sum is infinite which is a contradiction. A similar line of reasoning holds for the column sum constraints. □
Lemma 1
-
Consider the partitioned topology matrix given in Figure 4 for an arbitrary ring topology on n nodes with n even. If n(A,B,C,D)=n(E,F,G,H), that is, the number of ones in the top half is the same as the number of ones in the bottom half, then n(B)=n(H).
Proof
-
By the premise and the additivity of n(•), we see that
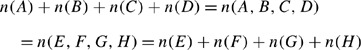
Since the topology matrix is symmetric, we know that n(C)+n(D)=n(C,D)=n(E,F)=n(E)+n(F). From above, this means that n(A)+n(B)=n(G)+n(H). But by symmetry of the topology matrix, n(A)=n(B) and n(G)=n(H) from which the result follows. □
Theorem 2
-
Consider a ring topology on n nodes with n even. Then, the following constraint holds:

Proof
-
From Lemma 1, it suffices to show that n(A,B,C,D)=n(E,F,G,H). This fact will be shown by first establishing this relationship for a specific topology matrix on n nodes and then showing that the result is true for any other topology matrix on n nodes. Consider the ring topology with nodes in clockwise order: 1,2,…,n,1 and corresponding matrix:
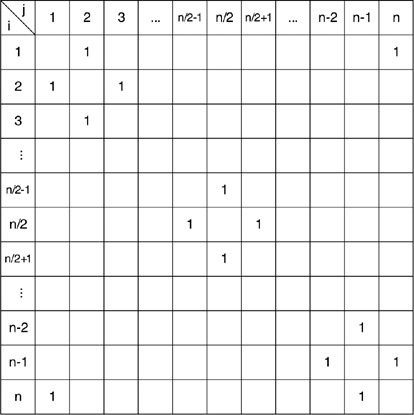
n(A) will equal n/2−1 since it corresponds to the link sequence {(1,2),(2,3),…,(n/2−1,n/2)}. Also, n(H) will equal (n/2)−1 since it will correspond to the link sequence {(n/2+1,n/2+2),(n/2+2,n/2+3),…,(n−1,n)}. Now consider the original sequence of nodes shown in clockwise order as: 1,2,…,i−1,i,i+1,i+2…,n and suppose that the nodes i and i+1 are switched to obtain a new sequence 1,2,…,i−1,i+1,i,i+2…,n. The topology matrix for this new sequence will be the same except for changes related to the indices for i−1,i,i+1,i+2. The submatrices for the first and second topologies for the indices in question are thus:
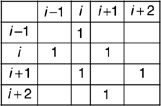
and
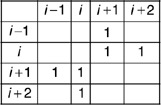
respectively. The row sums for these selected rows are clearly the same and this combined with the fact that the other parts of the topology matrix are not changed implies that the number of ones in the upper half of the matrix is still the same as the number of ones in the lower half as was the case with the initial ring topology. Thus, permutations of two contiguous nodes at a time does not alter this fact. Since any topology on n nodes can be obtained by a finite sequence of permutations of pairs of contiguous nodes, this means that n(A,B,C,D)=n(E,F,G,H) so that the desired result follows. □
Remark
-
In the proof of Theorem 2, there was an implicit assumption that there were at least four nodes. If this is not the case and n is even, then there would only be two nodes for which the result is trivially true.
Theorem 3
-
Consider a ring topology on n nodes with n even. Then, the following constraints hold:
(a)
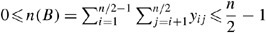
(b)
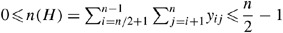
Proof
-
The lower bounds for (a) and (b) are obvious since y ij ∈{0,1}. In light of Theorem 2, it suffices to show that the upper bound holds for either (a) or (b). Suppose to the contrary that
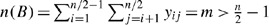 . But by symmetry n(A)=n(B). By Theorem 2, n(B)=n(H) and by symmetry n(G)=n(H). Hence, n(A,B,G,H)= 4m>2n−4. Since the total number of ones in the topology matrix is 2n, this means that 4m∈{2n−3,2n−2,2n−1,2n} or that m∈{n/2−3/4,n/2−1/2,n/2−1/4,n/2}. Since n is an even integer and m is an integer, the only value that is possible is m=n/2. This would mean that n(A,B,G,H)=2n or that the first n/2 nodes {1,2,…,n/2−1,n/2} form a ring but are not attached to the second set of nodes {n/2+1,n/2+2,…,n−1,n}. Clearly, this is a violation of all n nodes forming one ring. Hence, (a) and (b) hold. □
. But by symmetry n(A)=n(B). By Theorem 2, n(B)=n(H) and by symmetry n(G)=n(H). Hence, n(A,B,G,H)= 4m>2n−4. Since the total number of ones in the topology matrix is 2n, this means that 4m∈{2n−3,2n−2,2n−1,2n} or that m∈{n/2−3/4,n/2−1/2,n/2−1/4,n/2}. Since n is an even integer and m is an integer, the only value that is possible is m=n/2. This would mean that n(A,B,G,H)=2n or that the first n/2 nodes {1,2,…,n/2−1,n/2} form a ring but are not attached to the second set of nodes {n/2+1,n/2+2,…,n−1,n}. Clearly, this is a violation of all n nodes forming one ring. Hence, (a) and (b) hold. □
Theorem 4
-
Consider a ring topology on n nodes with n even. Then, the following constraints hold:
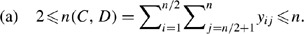
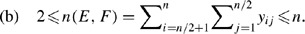
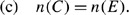
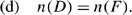
Proof
-
Given the symmetry of the topology matrix, n(C,D)=n(E,F) so it suffices to prove part (a) or (b). To show the upper bound in part (a), suppose to the contrary that n(C,D)>n. By symmetry, this would mean that n(E,F)>n so that n(C,D,E,F)>2n which is not possible since the total number of ones is 2n. Now for the lower bound to part (a), suppose to the contrary that n(C,D)=m<2, so m⩽1. This means that n(C,D,E,F)=2m⩽2 or that m∈{0,1}. But since n(A,B,G,H)=2n−2m and n(A)=n(B)=n(G)=n(H) by symmetry and Theorem 2, this means that n(A)=(2n−2m)/4=1/2n−1/2m. Since n(A) is an integer (and n even), this forces m=0 so that the first n/2 nodes {1,2,…,n/2−1,n/2} form a ring but are not attached to the second set of nodes {n/2+1,n/2+2,…,n−1,n}. Clearly, this is a violation of all n nodes forming one ring. Hence, (a) and (b) hold. Parts (c) and (d) follow easily from the symmetry of the topology matrix. □
Theorem 5
-
Consider a ring topology on n nodes with n even or odd. Then, the following constraint holds: f ω(=(o,d))ij =f ω(=(d,o))ji .
Proof
-
If n=odd, then there is only one shortest path between any OD pair, (o,d). Therefore, if an arc(i,j) lies on the shortest path, then f ω(=(o,d))ij =1=f ω(=(d,o))ji .
If n=even and DIST(o,d)<⌊n/2⌋, then DIST(d,o)<⌊n/2⌋. Thus, f ω(=(o,d))ij =1=f ω(=(d,o))ji .
If n=even and DIST(o,d)=⌊n/2⌋, then there are two paths between the OD pair, (o,d), which have the same distance ⌊n/2⌋. Therefore, either path of the two is acceptable. By this reason, if n=even, we can arbitrarily enforce that f ω(=(o,d))ij =f ω(=(d,o))ji . □
Remark
-
Since the constraint in Theorem 5 comes from the distance matrix, it is compatible with the shortest path constraints.
Theorem 6
-
Consider a ring topology on n nodes with n even. Then, the following constraint holds:
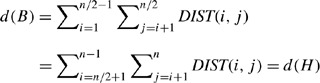
Proof
-
By Theorem 1, we know that each row sum of the distance matrix must be the same. Hence, d(A,B,C,D)=d(E,F,G,H). But since d(•) is additive, this means that d(A)+d(B)+d(C)+d(D)=d(E)+d(F)+d(G)+d(H). Since the distance matrix is symmetric, d(C)+d(D)=d(C,D)=d(E,F)=d(E)+d(F) implying that d(A)+d(B)=d(G)+d(H). Again by symmetry, d(A)=d(B),d(G)=d(H) so that 2d(B)=2d(H) so that the desired result follows. □
Statement of Heuristic Algorithm
Step 1: Initialization
- (a):
-
Generate a vector of nodes node init={1,i 2,…,i n } where {i 2,…,i n } is a permutation of {2,…,n}.
- (b):
-
Using node init, compute the corresponding topology matrix Y and set Y init=Y.
- (c):
-
Compute the distance matrix DIST from Y init by (14) and set DIST init=DIST.
- (d):
-
Compute the total traffic congestion TTC by (15) and set TTC init=TTC.
Step 2: Two-Opt Swap Procedure
-
a)
Set node base=node init, and count=1. FOR k=2 to n DO (k is an index number of node base.)
-
b)
Set center=node base(k), where center is the kth node number in node base. For i=2,…,n,i≠k, DO
-
i)
Exchange the position of the kth node (center) and the ith node in node base
-
ii)
Using node base with i and k swapped, compute the corresponding topology matrix Y and set Y base=Y
-
iii)
Compute the distance matrix DIST from Y base and set DIST base=DIST
-
iv)
Compute TTC and TTC diff=TTC−TTC init
-
v)
Save TTC, TTC diff and the swapped node base in a data structure as follows: DATA(count)={[TTC,TTC diff, node base]} and set count=count+1.
-
vi)
Reset node base to node init. END DO Reset node base to node init. END DO
-
i)
Step 3: Decision rules to find improved topologies
- (a):
-
Find vectors of [TTC,TTC diff,node base]∈DATA which satisfy TTC diff⩽0 (if there is a pair of vectors whose (TTC,TTC diff) values are the same, then choose only one); set the number of topologies with an improved total traffic congestion as m.
- (b):
-
Among the m topologies selected in Step 3a, pick out four of them corresponding to:
• The largest negative value of TTC diff (RULE 1)
• The second largest negative value of TTC diff (RULE 2)
• The least negative (or zero) value of TTC diff (RULE 3)
• The second least negative value of TTC diff (RULE 4)
- (c):
-
Save each topology from RULES 1–4.
Step 4: Iterations
- (a):
-
Take each of the four topologies selected in Step 3 and apply the swapping procedure Step 2 to obtain a new topology with the most improvement.
- (b):
-
Record relevant information as before.
- (c):
-
Repeat until no further improvement in TTC values.
Step 5: Final Step
Choose [TTC,node base] which has the smallest TTC among the TTC values collected from the result in Step 4 to each RULE.
End of procedure.
Since the above procedures are simple, they can be easily coded by many languages such as C (C++) or a simulation tool such as MATLAB.
Rights and permissions
About this article
Cite this article
Shim, Y., Gabriel, S., Desai, A. et al. A fast heuristic method for minimizing traffic congestion on reconfigurable ring topologies. J Oper Res Soc 59, 521–539 (2008). https://doi.org/10.1057/palgrave.jors.2602360
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1057/palgrave.jors.2602360




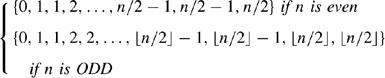
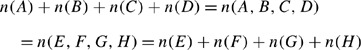




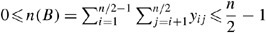
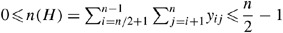
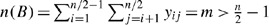 . But by symmetry n(A)=n(B). By Theorem 2, n(B)=n(H) and by symmetry n(G)=n(H). Hence, n(A,B,G,H)= 4m>2n−4. Since the total number of ones in the topology matrix is 2n, this means that 4m∈{2n−3,2n−2,2n−1,2n} or that m∈{n/2−3/4,n/2−1/2,n/2−1/4,n/2}. Since n is an even integer and m is an integer, the only value that is possible is m=n/2. This would mean that n(A,B,G,H)=2n or that the first n/2 nodes {1,2,…,n/2−1,n/2} form a ring but are not attached to the second set of nodes {n/2+1,n/2+2,…,n−1,n}. Clearly, this is a violation of all n nodes forming one ring. Hence, (a) and (b) hold. □
. But by symmetry n(A)=n(B). By Theorem 2, n(B)=n(H) and by symmetry n(G)=n(H). Hence, n(A,B,G,H)= 4m>2n−4. Since the total number of ones in the topology matrix is 2n, this means that 4m∈{2n−3,2n−2,2n−1,2n} or that m∈{n/2−3/4,n/2−1/2,n/2−1/4,n/2}. Since n is an even integer and m is an integer, the only value that is possible is m=n/2. This would mean that n(A,B,G,H)=2n or that the first n/2 nodes {1,2,…,n/2−1,n/2} form a ring but are not attached to the second set of nodes {n/2+1,n/2+2,…,n−1,n}. Clearly, this is a violation of all n nodes forming one ring. Hence, (a) and (b) hold. □