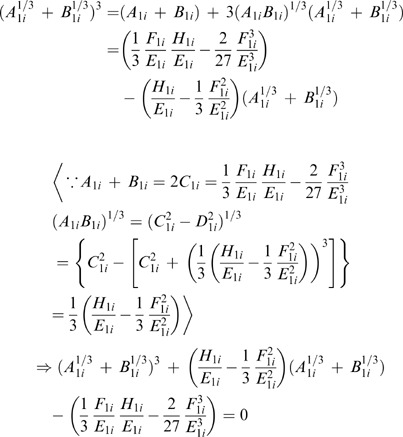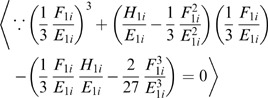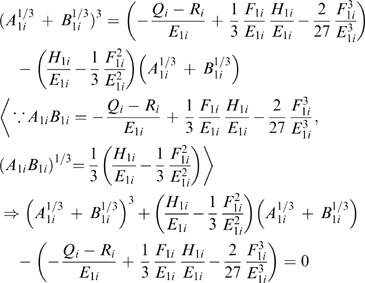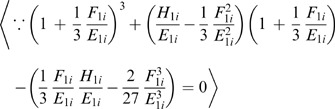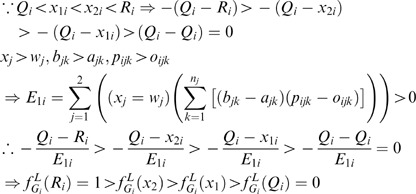Abstract
A fuzzy MCDM approach is applied to the stock selection problem, where the proposed approach can deal with qualitative information in addition to quantitative information. A hierarchy of major–sub criteria is then established to reduce the dependence between criteria. The ratings of alternatives versus qualitative sub-criteria and the weights of major- and sub-criteria are assessed in linguistic terms represented by fuzzy numbers. Each sub-criterion is in a benefit, cost, or balanced nature. New standardization methods for fuzzy numbers in the cost and balanced nature are presented. The algorithms of membership functions of the final aggregation are completely developed instead of approximation. The final aggregations in fuzzy numbers are then defuzzified to crisp values in order to rank the performance of alternatives. Moreover, the ratio of market price to performance (PP) is suggested to filter the over/under-pricing of alternatives. A set of buying/selling strategies are recommended according to the performance and PP. An empirical example then demonstrates the processing of the proposed approach.




Similar content being viewed by others
References
Black F and Scholes M (1973). The pricing of options and contract liabilities. J Political Econom 81: 637–659.
Chen MJ, Yan SY and Lin CJ Lin (1996). The application of fuzzy multiple attribute decision making in stock selection. J Mngt Sci 13 (2): 227–248.
Chen SJ and Hwang CL (1992). Fuzzy Multiple Attribute Decision Making. Springer: Berlin.
Cheng CH (1998). A new approach for ranking fuzzy numbers by distance method. Fuz Sets Sys 95 (3): 307–317.
Choobineh F and Li H (1993). An index for ordering fuzzy numbers. Fuz Sets Sys 54: 287–294.
Chu TC and Tsao CT (2002a). Ranking fuzzy numbers with an area between the centroid point and original point. Com Math Applications 43: 111–117.
Chu TC and Tsao CT (2002b). A novel defuzzifying approach to car evaluation and selection under fuzzy environment. Int J Uncertainty, Fuz Knowledege-Based Sys 10 (3): 309–326.
Dourra H and Siy P (2002). Investment using technical analysis and fuzzy logic. Fuz Sets Sys 127: 221–240.
Dubois D and Prade H (1978). Operations on fuzzy numbers. Int J Sys Sci 9 (6): 613–626.
Ehrgott M, Klamroth K and Schwehm C (2004). An MCDM approach to portfolio optimization. Eur J Opl Res 155: 752–770.
Fortemps P and Roubens M (1996). Ranking and defuzzification methods based on area compensation. Fuz Sets Sys 82 (3): 319–330.
Gordon MJ (1962). The Investment Financing and Valuation of the Corporation. Homewood IL: Richard D Irwin.
Hsu HM and Chen CT (1997). Fuzzy credibility relation method for multiple criteria decision-making problems. Info Sci 96: 79–91.
Kaufmann A and Gupta MM (1991). Introduction to Fuzzy Arithmetic: Theory and Application. VanNostrand Reinhold: New York.
Lee KM, Cho CH and Lee-Kwang H (1994). Ranking fuzzy values with satisfaction function. Fuz Sets Sys 64: 295–311.
Merton RC (1973). Theory of Rational Option Pricing. Bell J Eco and Mngt Sci 4: 141–183.
Miller MH and Modigliani F (1961). Dividend Policy, Growth and the Valuation of Shares. J Bus 34: 411–433.
Modarres M and Sadi-Nezhad S (2001). Ranking fuzzy numbers by preference ratio. Fuz Sets Sys 118 (3): 429–436.
Ohlson JA (1995). Earnings, book values, and dividends in equity valuation. Contem Acct Res 11 (2): 661–687.
Ross SA (1976). The arbitrage theory of capital asset pricing. J Eco Theory Dec 1976: 341–360.
Serguieva A and Hunter J (2004). Fuzzy interval methods in investment risk appraisal. Fuz Sets Sys 142: 443–466.
Sharpe WF (1964). Capital asset prices: a theory of market equilibrium under conditions of risk. J Fin Sep 1964: 425–442.
Sue CF and Chen YC (1990). Business financial condition rating — the application of fuzzy sets on accounting. J Taipei City Bank 21 (11): 67–85.
Tsao CT (2002). Evaluating investment values of stocks using a fuzzy TOPSIS approach. J Inf Opti Sci 4 (2): 373–396.
Tsao CT and Chu TC (2002). An improved fuzzy MCDM model based on ideal and anti-ideal concepts. J Opns Res Soc Jap 45 (2): 185–197.
Williams JB (1938). The Theory of Investment Value. Harvard University Press: Cambridge, Mass.
Wu HC (2004). Pricing European options based on the fuzzy pattern of Black–Scholes formula. Comput Opns Res 31: 1069–1081.
Yao JS and Wu K (2000). Ranking fuzzy numbers based on decomposition principle and signed distance. Fuz Sets Sys 116 (2): 275–288.
Zadeh LA (1965). Fuzzy sets. Inf Control 8: 338–353.
Zadeh LA (1975). The concept of a linguistic variable and its application to approximate reasoning—I. Inf Sci 8: 199–249.
Zmeskal Z (2001). Application of the fuzzy-stochastic methodology to appraising the firm value as a European call option. Eur J Opl Res 135: 303–310.
Acknowledgements
This research was supported by National Science Council, Taiwan, ROC, under Grant NSC94-2416-H-251-011.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Appendix presents the proofs of Property 1–Property 4.
Proof of Property 1
-
For x i1k ′∈R, let x i1k ′=μ 1k ′+ɛσ 1k ′, ɛ∈R. If R is cut into three segments, ɛ is in one of the situations:
-
1)
ɛ⩽−2
-
2)
−2<ɛ<2 (or −2<ɛ⩽0, 0⩽ɛ<2)
-
3)
ɛ⩾2
It is to prove that 0⩽x i1k ⩽1 for x i1k ′∈{B, C, M}.Using Equation (10) for x i1k ′∈B:
When ɛ⩽−2, μ 1k ′+ɛσ 1k ′⩽μ 1k ′−2σ 1k ′ → x i1k =0.
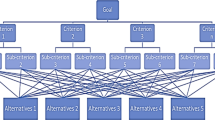
When −2<ɛ<2,
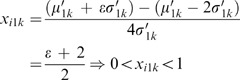
When ɛ⩾2, μ 1k ′+ɛσ 1k ′⩾μ 1k ′+2σ 1k ′ → x i1k =1.Using Equation (11) for x i1k ′∈C:
When ɛ⩽−2, μ 1k ′+ɛσ 1k ′⩽μ 1k ′−2σ 1k ′ → x i1k =1.
When −2<ɛ<2,

When ɛ⩾2, μ 1k ′+ɛσ 11′⩾μ 1k ′+2σ 1k ′ → x i1k =0.Using Equation (12) for x i1k ′∈M:
When ɛ⩽−2, μ 1k ′+ɛσ 1k ′⩽μ 1k ′−2σ 1k ′ → x i1k =0.
When −2<ɛ⩽0,
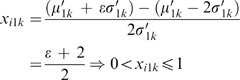
When 0⩽ɛ<2,
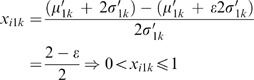
When ɛ⩾2, μ 1k ′+ɛσ 1k ′⩾μ 1k ′+2σ 1k ′ → x i1k =0.
-
1)
Proof of Property 2
-
Suppose A i ′=(o i ′, p i ′, q i ′, r i ′)∈C, where i=1∼n: n is the number of fuzzy numbers. Using Equation (15), the transformed numbers A i =(o i , p i , q i , r i ).
(1) It is to prove
(r 1−o 1):(r 2−o 2): … :(r n −o n )=(r 1′−o 1′):(r 2′−o 2′): … :(r n ′−o n ′) if the relative dispersions of the transformed numbers are equal to those of the original numbers:

(2) It is to prove
(p i −o i ):(q i −p i ):(r i −q i )=(r i ′−q i ′):(q i ′−p i ′):(p i ′−o i ′) if the transformed shapes are a reverse to the original shapes:
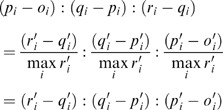
Proof of Property 3
-
Let A 1′=(o 1′, p 1′, q 1′, r 1′), A 2′=(o 2′, p 2′, q 2′, r 2′), A 1′, A 2′⊂A i ′, and A i ′=(o i ′, p i ′, q i ′, r i ′)∈M. Using Equation (16) A 1′ and A 2′ are standardized to be A 1=(o 1, p 1, q 1, r 1) and A 2=(o 2, p 2, q 2, r 2). It is to prove (1) if A 1′ is closer to max i r′/2 than A 2′, then A 1>A 2. 2. A i ∈[0, 1].
(1) If A 1′ is closer to max i r′ i /2 than A 2′ then the distance from A 1′, to max i r′ i /2 is shorter than that from A 2′ to max i r′ i /2:
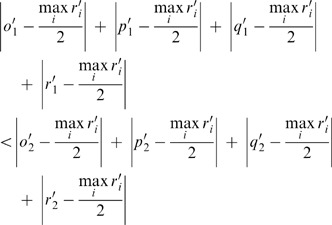
Multiply the above equation by 2/max i r′ i , where max i r′ i >0,
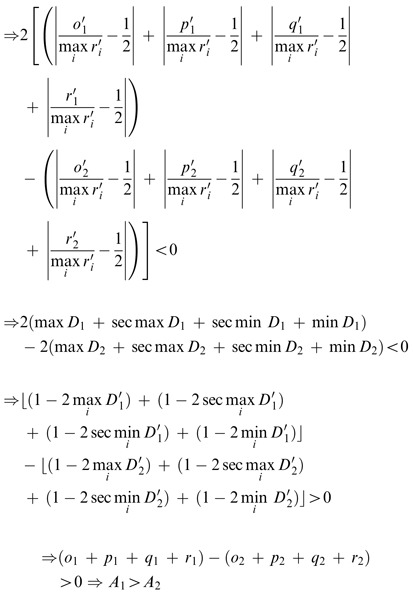
(2)
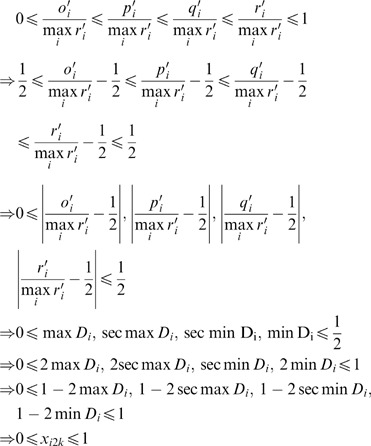
Proof of Property 4
-
-
1)
For G i =[Q i , R i , Y i , Z i ],
 (x=Q
i
)=0,
(x=Q
i
)=0,  (x=R
i
)=1,
(x=R
i
)=1, 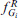 (x=Y
i
)=1, and
(x=Y
i
)=1, and 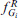 (x=Z
i
)=0.
(x=Z
i
)=0. -
2)
 (x) is strictly increasing on x∈[Q
i
, R
i
] and
(x) is strictly increasing on x∈[Q
i
, R
i
] and 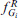 (x) is strictly decreasing on x∈[Z
i
, Y
i
].
(x) is strictly decreasing on x∈[Z
i
, Y
i
].
(1.1) To prove
 (x=Q
i
)=A
1i
1/3+B
1i
1/3−F
1i
/3E
1i
=0 is to prove A
1i
1/3+B
1i
1/3=F
1i
/3E
1i
, when x=Q
i
.
(x=Q
i
)=A
1i
1/3+B
1i
1/3−F
1i
/3E
1i
=0 is to prove A
1i
1/3+B
1i
1/3=F
1i
/3E
1i
, when x=Q
i
. 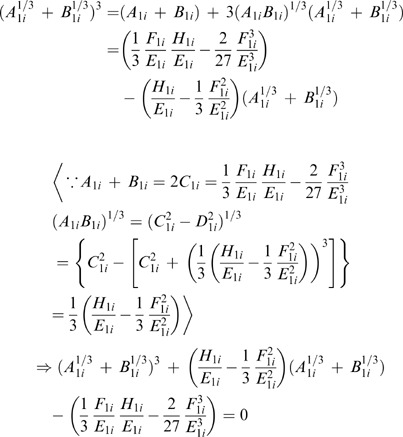
Solving the above equation, the real-number root of (A 1i 1/3+B 1i 1/3) is F 1i /3E 1i .
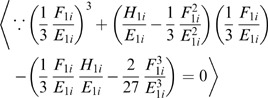
(1.2) To prove
 (x=R
i)=A
1i
1/3+B
1i
1/3−F
1i
/3E
1i
=1 is to prove A
1i
1/3+B
1i
1/3=1+F
1i
/3E
1i
, when x=R
i
.
(x=R
i)=A
1i
1/3+B
1i
1/3−F
1i
/3E
1i
=1 is to prove A
1i
1/3+B
1i
1/3=1+F
1i
/3E
1i
, when x=R
i
. 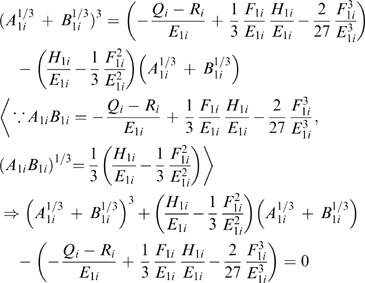
Solving the above equation, the real-number root of (A 1i 1/3+B 1i 1/3) is (1+F 1i /3E 1i ).
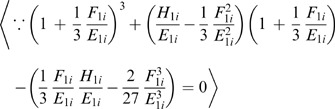
(1.3) It can be proven that
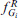 (x=Y
I)=1 and
(x=Y
I)=1 and  (x=Z
i
)=0 by the same logic. The proofs are omitted.
(x=Z
i
)=0 by the same logic. The proofs are omitted.(2) Suppose Q i <x 1i <x 2i <R i and Y i <x 3i <x 4i <Z i . To prove strictly increasing
 is to prove 0=
is to prove 0= (Q
i
)<
(Q
i
)< (x
1i
)<
(x
1i
)< (x
2i
)<
(x
2i
)< (R
i
)=1. To prove strictly decreasing
(R
i
)=1. To prove strictly decreasing 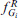 is to prove 1=
is to prove 1=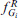 (Y
i
)>
(Y
i
)>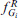 (x
3i
)>
(x
3i
)>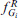 (x
4i
)>
(x
4i
)> (Z
i
)=0.
(Z
i
)=0. 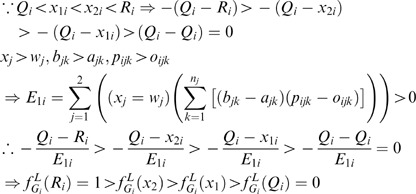
It can be proven that 1=
 (Y
i
)>
(Y
i
)> (x
3i
)>
(x
3i
)> (x
4i
)>
(x
4i
)>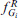 (Z
i
)=0 by the same logic. The proofs are omitted.
(Z
i
)=0 by the same logic. The proofs are omitted. -
1)
Rights and permissions
About this article
Cite this article
Tsao, CT. A fuzzy MCDM approach for stock selection. J Oper Res Soc 57, 1341–1352 (2006). https://doi.org/10.1057/palgrave.jors.2602139
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1057/palgrave.jors.2602139




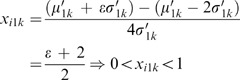

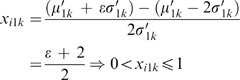
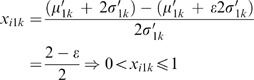

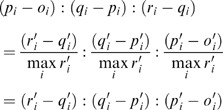
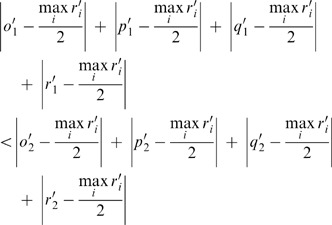
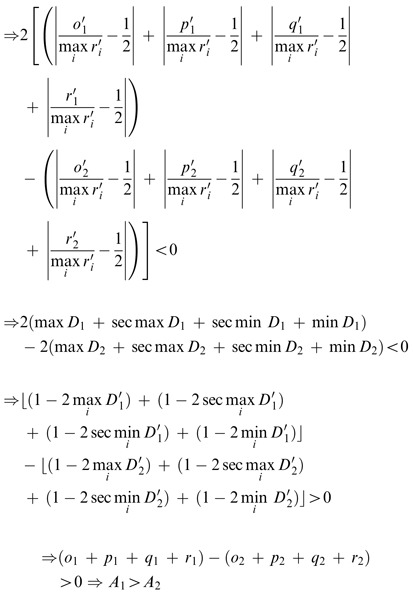
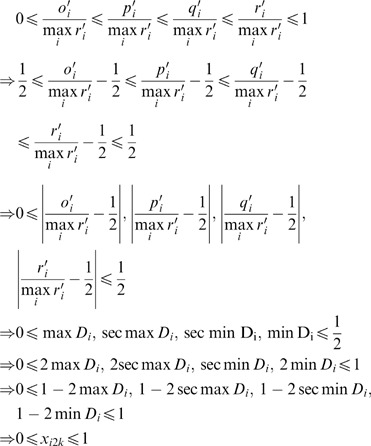
 (x=Q
i
)=0,
(x=Q
i
)=0, 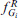 (x=Y
i
)=1, and
(x=Y
i
)=1, and  (x) is strictly increasing on x∈[Q
i
, R
i
] and
(x) is strictly increasing on x∈[Q
i
, R
i
] and