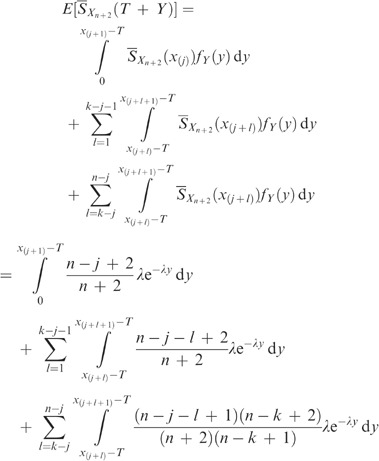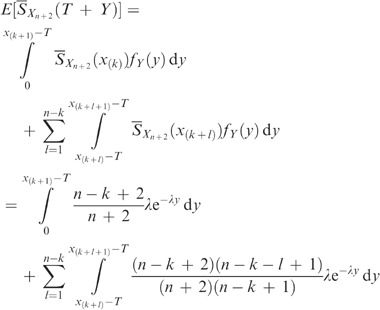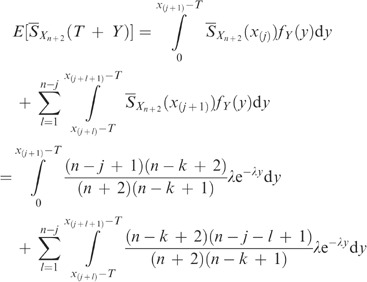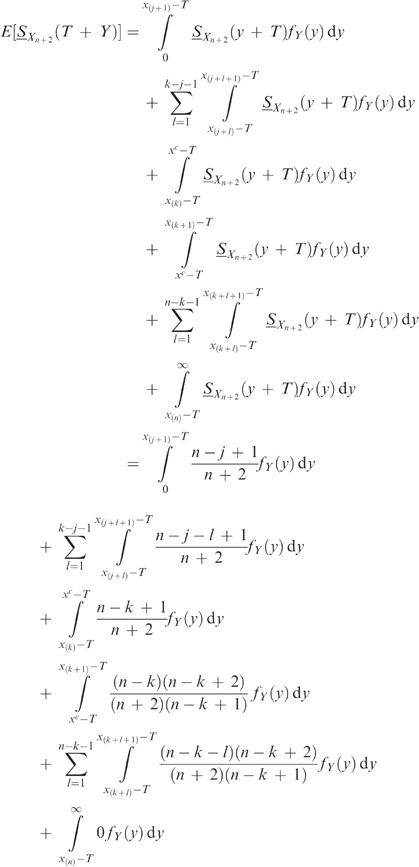Abstract
We consider opportunity-based age replacement (OAR) using nonparametric predictive inference (NPI) for the time to failure of a future unit. Based on n observed failure times, NPI provides lower and upper bounds for the survival function for the time to failure Xn+1 of a future unit which lead to upper and lower cost functions, respectively, for OAR based on the renewal reward theorem. Optimal OAR strategies for unit n+1 follow by minimizing these cost functions. Following this strategy, unit n+1 is correctively replaced upon failure, or preventively replaced upon the first opportunity after the optimal OAR threshold. We study the effect of this replacement information for unit n+1 on the optimal OAR strategy for unit n+2. We illustrate our method with examples and a simulation study. Our method is fully adaptive to available data, providing an alternative to the classical approach where the probability distribution of a unit's time to failure is assumed to be known. We discuss the possible use of our method and compare it with the classical approach, where we conclude that in most situations our adaptive method performs very well, but that counter-intuitive results can occur.

Similar content being viewed by others
References
Barlow RE and Proschan F (1965). Mathematical Theory of Reliability. Wiley: New York.
Mazzuchi TA and Soyer R (1996). A Bayesian perspective on some replacement strategies. Reliab Eng System Safety 51: 295–303.
Sheu SH, Yeh RH, Lin YB and Juang MG (2001). A Bayesian approach to an adaptive preventive maintenance model. Reliab Eng System Safety 71: 33–44.
Apeland S and Scarf PA (2003). A fully subjective approach to capital equipment replacement. J Opl Res Soc 54: 371–378.
Percy DF (2002). Bayesian enhanced strategic decision making for reliability. Eur J Opl Res 139: 133–145.
Coolen-Schrijner P and Coolen FPA (2004). Nonparametric predictive inference for age replacement with a renewal argument. Qual Reliab Eng Int 20: 203–215.
Coolen-Schrijner P and Coolen FPA (2004). Adaptive age replacement strategies based on nonparametric predictive inference. J Opl Res Soc 55: 1281–1297.
Dekker R and Dijkstra MC (1992). Opportunity-based age replacement: exponentially distributed times between opportunities. Nav Res Logist 39: 175–190.
Jhang JP and Sheu SH (1999). Opportunity-based age replacement policy with minimal repair. Reliab Eng System Safety 64: 339–344.
Hill BM (1968). Posterior distribution of percentiles: Bayes’ theorem for sampling from a population. J Am Statist Assoc 63: 677–691.
Augustin T and Coolen FPA (2004). Nonparametric predictive inference and interval probability. J Statist Plann Inference 124: 251–272.
De Finetti B (1974). Theory of Probability. Wiley: London.
Hill BM (1988). De Finetti's theorem, induction, and A( n ) or Bayesian nonparametric predictive inference. In: Bernardo JM et al (eds). Bayesian Statist 3: 211–241.
Coolen FPA, Coolen-Schrijner P and Yan KJ (2002). Nonparametric predictive inference in reliability. Reliab Eng System Safety 78: 185–193.
Coolen FPA and Yan KJ (2004). Nonparametric predictive inference with right-censored data. J Statist Plann Inference 126: 25–54.
The R project for Statistical Computing. www.r-project.org.
Acknowledgements
This research is supported by the UK Engineering and Physical Research Sciences Council, Grant GR/R92530/01.
Author information
Authors and Affiliations
Corresponding author
Appendix A
Appendix A
Derivation of (13)
We derive an expression for E[Lop(T)] which is similar to Equation (9) of Dekker and Dijkstra,8 but in a form more suitable for this paper. This expression holds for exponentially distributed Y, with probability density function f Y (.).

where the penultimate equality follows from the fact that S Y (x)=E[Y]dF Y (x)/dx, as Y has an Exponential distribution.
Proof of Lemma 1
-
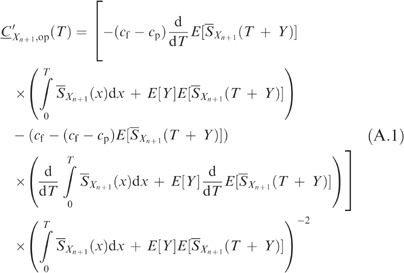
Here,
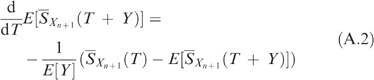
see, for example Dekker and Dijkstra,8 and
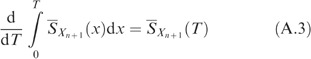
Substituting (A.2) and (A.3) into (A.1) yields
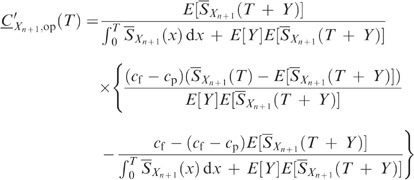
As the last expression is equal to
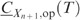 , and both
, and both 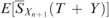 and
and 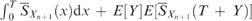 are positive, we have, for T∈[x(j), x(j+1)) and j=0, …, n
are positive, we have, for T∈[x(j), x(j+1)) and j=0, …, n 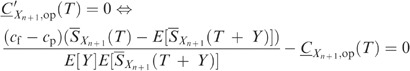
Obviously, we only prove this for T∈(x(j), x(j+1)) and j=0, …, n−1, as the second derivatives do not exist in the observed values x(j). Differentiating Cop(T) of Equation (14) with respect to T, and using (A.2) and (A.3) with Xn+1 replaced by X, obtain
where
Hence, as E[L(T)] and E[Lop(T)] are both strictly positive, we have
Now,
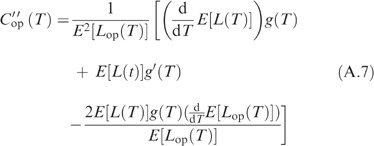
where
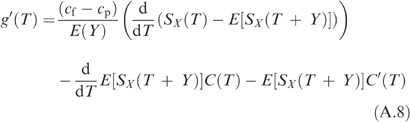
with C′(T) the first derivative of the age replacement cost function (11). Moreover, we have
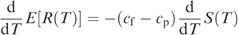
and using (A.2), with Xn+1 replaced by X,
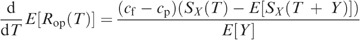
so that
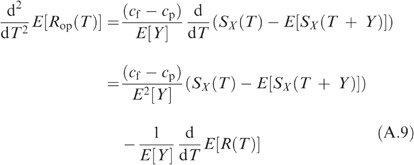
Substituting (A.9) into (A.8) yields
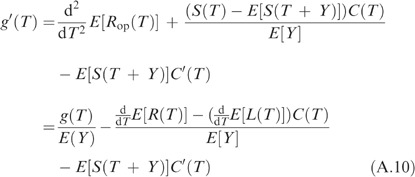
Differentiating the age replacement cost function C(T) (11) with the respect to T yields
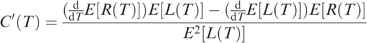
and since E[L(T)]>0 for all T>0,
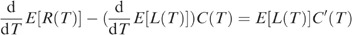
so that (A.10) can be written as
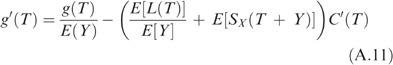
Using (A.11), we have
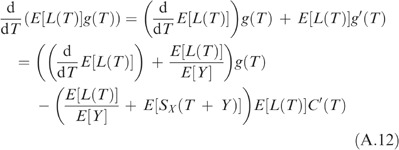
Substituting (A.12) into (A.7) yields
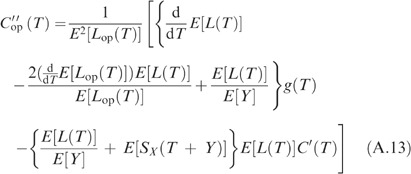
However, at the optimal OAR threshold Top* we have g(Top*)=0 according to (A.6). From Lemmas 2.2 and 3.2 of Coolen-Schrijner and Coolen6 we know that the first derivatives of our NPI based age replacement cost functions
 are all negative. Substituting the lower and upper survival functions in E[L(T)] and E[S
X
(T+Y)] yields corresponding lower and upper bounds which are all positive. Then, from (A.13), it follows that
are all negative. Substituting the lower and upper survival functions in E[L(T)] and E[S
X
(T+Y)] yields corresponding lower and upper bounds which are all positive. Then, from (A.13), it follows that 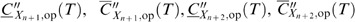 are all positive.
are all positive.
Proof of Lemma 3
-
-
1
T∈[x(j), x(j+1)) with j=0, …, k−1. In this case, Equation (32) can be obtained by noting that
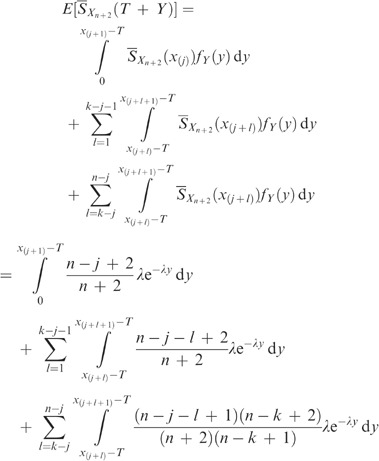
-
2
T∈[x(k), x(k+1)). In this case, Equation (33) can be obtained by noting that
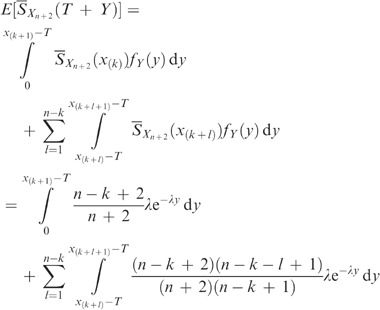
-
3
T∈[x(j), x(j+1) with j=k+1, …, n. In this case, Equation (34) can be obtained by noting that
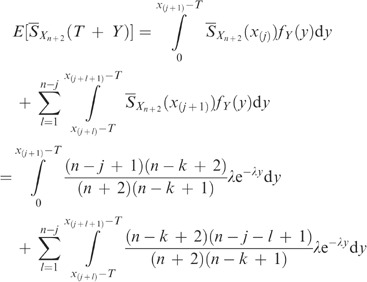
□
-
1
Proof of Lemma 6
-
We only prove part (a)-1 of the lemma, the proofs of the other parts are similar. Suppose T∈(x(j), x(j+1)] with j=0, …, k−1, then
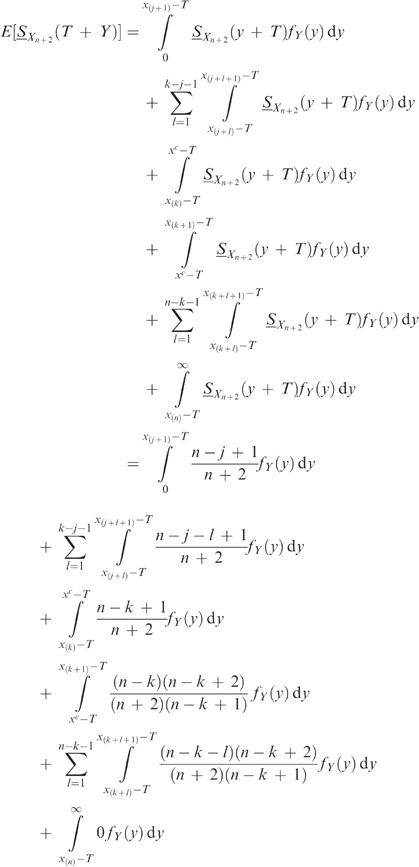
As Y has an Exponential distribution with parameter λ, the result follows.
Rights and permissions
About this article
Cite this article
Coolen-Schrijner, P., Coolen, F. & Shaw, S. Nonparametric adaptive opportunity-based age replacement strategies. J Oper Res Soc 57, 63–81 (2006). https://doi.org/10.1057/palgrave.jors.2601954
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1057/palgrave.jors.2601954


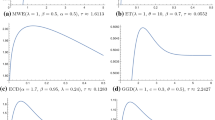


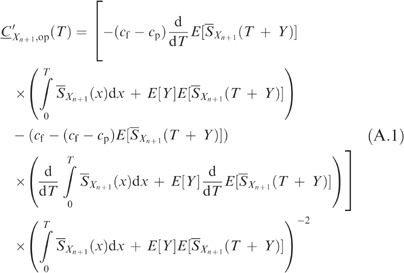
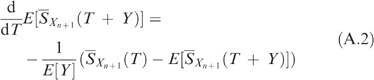
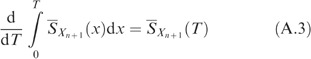
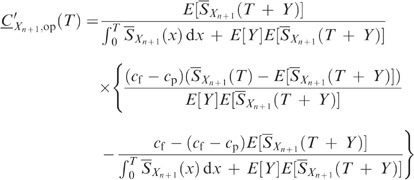
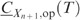 , and both
, and both 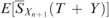 and
and 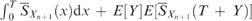 are positive, we have, for T∈[x(j), x(j+1)) and j=0, …, n
are positive, we have, for T∈[x(j), x(j+1)) and j=0, …, n 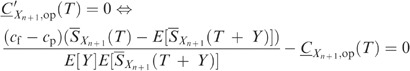
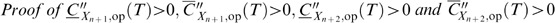
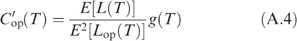
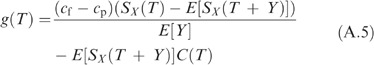
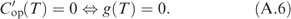
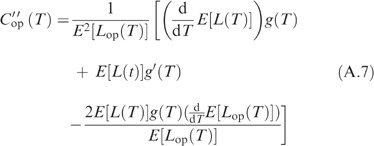
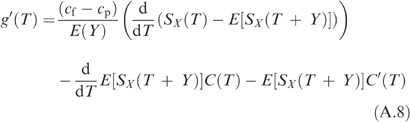
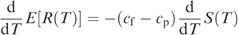
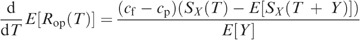
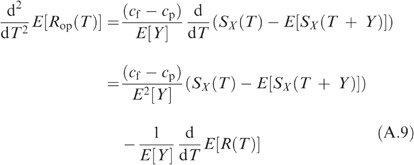
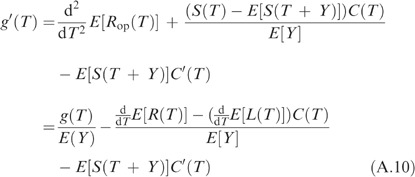
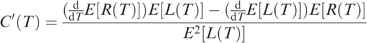
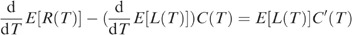
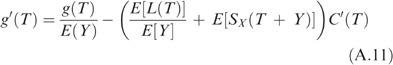
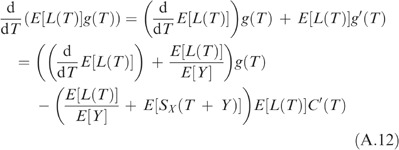
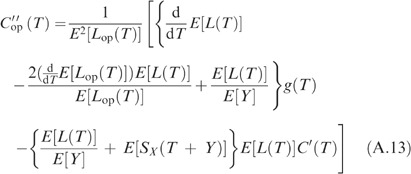
 are all negative. Substituting the lower and upper survival functions in E[L(T)] and E[S
X
(T+Y)] yields corresponding lower and upper bounds which are all positive. Then, from
are all negative. Substituting the lower and upper survival functions in E[L(T)] and E[S
X
(T+Y)] yields corresponding lower and upper bounds which are all positive. Then, from 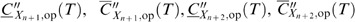 are all positive.
are all positive.