Abstract
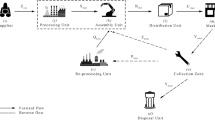
The production system using kanban was pioneered by Toyota Motor Company in Japan and subsequently it was adopted by numerous other Japanese and US companies for applying the just-in-time manufacturing principles. This research studies a single-stage supply chain system that is controlled by kanban mechanism. The supply chain system is modelled as a mixed-integer nonlinear programming (MINLP) problem. It is solved optimally by branch-and-bound method to determine the number of kanbans, batch size, number of batches, and the total quantity over one period. Meanwhile, the kanban operation between two adjacent plants is worked out considering the factors of loading and unloading time, and transport time. Coupled with plant-wide efforts for cost control and management commitment to enhance other measures of performance, a logistics system for controlling the production as well as the supply chain system is developed, which results in minimizing the total cost of the supply chain system. The results show that the improvements in reduction of inventory, wasted labour, and customer service in a supply chain are accomplished through the kanban mechanism.






Similar content being viewed by others
References
Tardif V and Maaseidvaag L (2001). An adaptive approach to controlling kanban systems. Eur J Opl Res 132: 411–424.
Herer YT and Shaolom L (2000). The kanban assignment problem—a nonintegral approach. Eur J Opl Res 120: 260–276.
Gupta SM and Al-Turki YAY (1997). An algorithm to dynamically adjust the number of kanbans in stochastic processing times and variable demand environment. Prod Planning Control 8: 133–141.
Sarker BR and Balan CV (1996). Operations planning for kanbans between two adjacent workstations. Comput Indust Eng 31: 221–224.
Sarker BR and Balan CV (1998). Operations planning for a single-stage kanban system operating under linear demand. Int J Prod Res 36: 357–375.
Sarker BR and Balan CV (1999). Operations planning for a multi-stage kanban system. Eur J Opl Res 112: 284–303.
Nori VS and Sarker BR (1996). Cyclic scheduling for a multi-product, single-facility production system operating under a just-in-time delivery policy. J Opl Res Soc 47: 930–935.
Nori VS and Sarker BR (1998). Optimum number of kanbans between two adjacent stations. Prod Planning Control 9: 60–65.
Parija GR and Sarker BR (1999). Operations planning in a supply chain system with fixed-interval deliveries of finished goods to multiple customers. IIE Trans 31(11): 1075–1082.
Hill RM (1999). The optimal production and shipment policy for the single-vendor single-buyer integrated production-inventory problem. Int J Prod Res 37: 2463–2475.
Liberopoulos G and Dallery Y (2003). Comparative modeling of multi-stage production-inventory control policies with lot sizing. Int J Prod Res 41: 1273–1298.
Axsater S and Rosling K (1999). Ranking of generalized multi-stage KANBAN policies. Eur J Opl Res 113: 560–567.
Krieg G and Kuhn H (2002). A decomposition method for multi-product kanban systems with setup times and lost sales. IIE Trans 34: 613–626.
Zhao X, Nakashima K and Zhang ZG (2002). Allocating kanbans for a production system in a general configuration with a new control strategy. IEEE Trans Systems, Man Cybernet 32: 446–453.
Askin RG, Mitwasi MG and Goldberg JB (1993). Determining the number of kanbans in multiitem just-in-time systems. IIE Trans 25: 89–98.
Amin M and Altiok T (1997). Control policies for multi-product, multi-stage manufacturing systems: an experimental approach. Int J Prod Res 35: 201–223.
Aytug H and Dogan CA (1999). Simulation analysis of order and kanban sequencing rules in a kanban-controlled flow shop. Simulation 72: 212–220.
Chauyet F, Herrmann WJ and Proth JM (2003). Optimization of cyclic production systems: a heuristic approach. IEEE Trans Robotics Automat 19: 150–155.
Horng HC and Cochran JK (2001). Project surface regions: a decision support methodology for multitasking workers assignment in JIT systems. Comput Indust Eng 39: 159–171.
Krajewski LJ, King BE, Ritzman LP and Wong DS (1987). Kanban MRP, and shaping the manufacturing environment. Mngt Sci 33: 39–57.
Duran MA and Grossmann NE (1986). An outer-approximation algorithm for a class of mixed-integer nonlinear programs. Math Programming 36: 307–339.
Wang H and Wang HP (1991). Optimum number of kanbans between two adjacent workstations in a JIT system. Int J Prod Econ 22: 179–188.
Acknowledgements
We are thankful to the anonymous referees for their critical comments, valuable suggestions, and corrections in the manuscript to improve the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Appendix A. Proof of Theorem 1
Appendix A. Proof of Theorem 1
From Equation (7),

subject to x 1, x 2, x 3⩾1 and integer, Q>0.
It can be easily shown that the function Equation (A1) is convex in Q and x i for i=1, 2, and 3. Hence, ∂Z/∂x i =0 for i=1, 2, 3 will lead to

Also, ∂A/∂Q=0 leads to

Substituting of the values of x 1 *, x 2 *, and x 3 * into Equation (A3), we have

where α=As 1+As 2 and β=H w(1−D/p 1)+H f(1−D/p 2). The results in (A4) leads to

Rights and permissions
About this article
Cite this article
Wang, S., Sarker, B. A single-stage supply chain system controlled by kanban under just-in-time philosophy. J Oper Res Soc 55, 485–494 (2004). https://doi.org/10.1057/palgrave.jors.2601699
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1057/palgrave.jors.2601699