Abstract
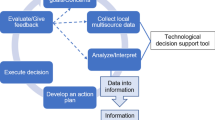
In this paper, a methodology for the ongoing diagnosis and facilitation (when required) of organizational change management programmes in an Australian University is described. The application of this methodology on an annual basis requires the assessment of research attitudes and behaviour, areas that have assumed considerable importance within universities around the world in the last decade. This increasing importance associated with research stems in part (a significant part) from the linkage of research quantum (output) of universities to their funding from government. The methodology developed in this paper embraces a wide range of OR-type techniques as well as a range of change management tools from human resources management. These two sets of techniques and tools work together as tools in their own right as well as providing the infrastructure to achieve the objectives. The developed methodology is an interesting blend of hard techniques and ‘soft’ approaches implemented through a soft heuristic, indeed this application is an example of mixed-mode modelling. The OR techniques (conventional in both their nature and application) are comprised of social judgement theory (for bench-marking research attitudes) and integer linear programming (for setting research targets). The results of the application of the developed methodology are discussed in terms of the effect on research quantum over a 5-year period. A similar methodology could be developed for a change process covering aspects of an organization other than research output in a number of countries.




Similar content being viewed by others
References
Mooney EL, Rardin RL and Parmenter WJ (1996). Large-scale classroom scheduling. IIE Trans 28: 369–378.
Stawicki RJ and Lawrence KD (1994). Using Markov chains to identify potential large donors. J Bus Forecast Meth Syst 13: 3–7.
Hemaida RS and Hupfer MA (1994/5). A multiobjective model for managing faculty resources. J Appl Bus Res 11: 24–29.
Fandel G and Gal T (2001). Redistribution of funds for teaching and research among universities: the case of North Rhine–Westphalia. Eur J Op Res 130: 111–120.
Bassin WM, Sellner RG and Bickers D (1997). How to prepare forecasts of enrolments for first year students. J Bus Forecast Meth Syst 16: 17–22.
Cassuto AE (1996). Forecasting enrolments of a newly created university. J Bus Forecast Meth Syst 15: 5–7.
Tomkins C and Green R (1998). An experiment in the use of data envelopment analysis for evaluating the efficiency of UK universities’ departments of accounting. Finan Accountability Mngt 4: 147–164.
Johnes G and Johnes C (1993). Measuring the research performance of UK economics departments: an application of data envelopment analysis. Oxford Econ Papers 45: 332–347.
Bowman JS, Chen FF, Tinkersley WB and Hilliard KR (1993). Patterns in MPA decision-making: an application of social judgment theory. Public Admin Quart 17: 356–372.
Mackintosh M, Jarvis R and Heery E (1994). On managing hybrids: some dilemmas in higher education management. Finan Accountability Mngt 10: 339–353.
Tischler L, Biberman J and Alkhafaiji A (1998). A new strategic planning model for universities undergoing transformation. Int J Commerce Mngt 8: 85–101.
Pratt M, Margaritis D and Coy D (1999). Developing a research culture in a university faculty. J Higher Educ Policy Mngt 21: 43–55.
Jack G and Lehaney B (2001). Management and wellbeing in the UK. In: Nicholls MG, Clarke SA and Lehaney B (eds) Mixed-mode Modelling — Facilitating Change in Organisations, Kluwer Academic Publishers: The Netherlands, pp 229–258.
Cargill BJ and Nicholls MG (1998). Establishing a Research culture and output in a hostile environment within an emerging Australian university — a case study. In: Fowler K and McClatchey M (eds). Proceedings of the 27th Annual Meeting of the Western Decision Sciences Institute, Reno, Nevada, USA, pp 567–572.
Cargill BJ, Nicholls MG and Dhir KS (2001). Tracking the progress of change management in a university environment using attitudinal and behavioural bench-marking. In: Li E and Wild R (eds). Proceedings of the 30th Annual Meeting of the Western Decision Sciences Institute, Vancouver, Canada, pp 539–542.
Nicholls MG, Clarke SA and Lehaney B (eds) (2001). Mixed-mode Modelling — Facilitating Change in Organisation, Kluwer Academic Publishers: The Netherlands.
Lehaney B (1996). Mixed-mode modelling. In: Johnson D and O’Brien F (eds). Operations Research Keynote Papers (1996), Operational Research Society of the United Kingdom, pp 150–157.
Argyris C and Schon DA (1978). Theory in Practice: Increasing Professional Effectiveness, Addison-Wesley: Leading, MA.
Hammond KR, Stewart TR, Brehmer B and Steinmann DO (1975). Social judgment theory. In: Kaplan M and Schwartz S (eds). Human Judgment and Decision Processes, Academic Press: New York, pp 271–312.
Hogarth RM (1980). Judgment and Choice: The Psychology of Decision Processes, Wiley: New York.
Zeleny M (1982). Multiple Criteria Decision Making, McGraw-Hill: New York.
Dhir KS (1988). Formulating policies for faculty promotion and tenure. In: Academic Chairpersons (eds). Search of Academic Quality, Center for Faculty Evaluation & Development, Kansas. State University.
Dhir KS, Cargill BJ and Nicholls MG (1999). International bench-marking of research culture and performance within a developing Australian university. In: Jenson R and Massoud M (eds) Proceedings of the 28th Annual Meeting of the Western Decision Sciences Institute, Puerto Vallarta, Mexico, pp 1170–1174.
Author information
Authors and Affiliations
Corresponding author
Additional information
Based on a paper delivered at the Operational Research Society's OR43 conference at Bath, UK, 2001.
Appendix A: The research targets model
Appendix A: The research targets model
Definition of variables
RQ i,k,t =the research output target (ie, average number of ‘publications’) for the kth category of Pool 1 research activity for a researcher of category i ability in year t (an integer); G l,m,t =the research output target (ie, the average number of grants) in the lth category of grant (Pool 2 research output) of magnitude m by a grant capable researcher in year (an integer) t.
Constraining factors (right-hand sides)
RQU i,k,t =the upper limit on the target research output for a category i researcher in research output category k in year t (influenced by the HRM model);
RQL i,k,t =the lower limit on the target research output for a category i researcher in research output category k in year t (influenced by HRM model);
GQU l,m,t =the upper limit on the targeted number of category l grants of magnitude m that a grant capable researcher could be expected to obtain in year t (influenced by the HRM model);
GQL l,m,t =the lower limit on the targeted number of category l grants of magnitude m that a grant capable researcher could be expected to obtain in year t (influenced by the HRM model);
RB1 k,t =is the research budget to be devoted to supporting category k research activity in year t;
TR1 t =is the total budget allocated to Pool 1 (publications) research activities in year t;
TR2 t =is the total budget allocated to Pool 2 (grants) research activities in year t;
TRB t =is the total budget allocated to research activities in Pool 1 and Pool 2 in year t.
Coefficients and parameters
NA i,t =the number of academic staff of research ability i in year t as determined by the HRM model (in which this is a variable);
N i,t =the number of category i researchers available for research activities in year t after taking into account the number of academics required for the completion of other activities (eg, teaching. administration and community/university service). An academic staff member is only classified as a researcher when they have a researcher classification (i>1) indicating that they are research active N t *=the number of grant capable researchers defined as:

where i * represents the minimum researcher category capable of obtaining a grant (N t * and N i,t are determined by the HRM model's NA i,t ). Note further that N i,t <TN t where TN t =the total number of academic staff in the School; o i,t =the proportion of available academic staff of research capability i who are on average available to undertake research (ie, after taking into account teaching, administration and community university service activities). This coefficient is determined in the HRM model. Note:

that is, the lowest research ability classification is completely devoted to activities other than research and:

w k,t =the weight assigned by either the School or DEST to the kth research output category in Pool 1 in year t (a means of prioritizing the research activity);
g l,t =the weight assigned by either the School or DEST to the lth research grant in Pool 2 in year t (a means of prioritizing the research activity);
c i,k,t =the average cost of obtaining one unit of output (publication) in research output category k by a researcher of ability i in year t;
y l,m,t =the average cost of obtaining one category l research grant of magnitude m by a research grant capable researcher in year t;
J 1=the sub-set of integer variables;
The simplified mathematical model is:

subject to










In model (1), the objective is to maximize the weighted publications and grants classifications research output thereby maximizing the research funding to be allocated by the University to the School. Note that the publications and grants sections of the objective function are both in the same units of measurement. This ILP problem is readily and quickly solved using the standard branch and bound approach available in any commercial optimization package. The time subscript is maintained since the model will be used inter-temporally in the solution heuristic.
Constraints (1a) and (1b) set the upper and lower limits on the average research output (target research output) that may be assigned in research category k associated with a category i researcher in year t. Constraints (1c) and (1d) do the same as (1a) and (1b) but deal with Pool 2 research activities, that is, the number of grants of category l of magnitude m (eg, a grant of the magnitude $100 000–$150 000). These limits are set in part by senior management of the School and to some extent are also determined by the HRM model. Note also that these limits for grants and publication categories are set with the interdependence that exists between them taken into account. The upper limits of the publications count and grant numbers for example, must be set so that an individual category i researcher, might be able to achieve them both given that their work load is devoted completely to research activities. The fact that other activities need to be undertaken is taken into account with the removal of the equivalent number of staff as discussed in the definition of NA i,t and with respect to constraint (1i) below.
Constraint (1e) ensures that the total cost of research output targets across publication category k for all active researchers, will not exceed the amount allocated in the budget for these specific activities. Constraint (1f) on the other hand, ensures that the total amount spent on research activities in Pool 1 (publication) research activities across the School will not exceed the allocated budget. Constraint (1g) ensures that the total amount spent on obtaining all research grants (ie, Pool 2 research activities) will not be exceeded. Constraint (1h) makes sure that the total amount spent on research activities on all Pool 1 and Pool 2 research activities will not exceed the total research budget allocated by the School. These budget limits are influenced by available funding to the School as well as what is seen as areas of priority.
Constraint (1i) establishes the average number of researchers of each classification of ability that are available to undertake research activity in year t. This is effectively discounting the proportion of the time available by each category of researcher available (as determined by the HRM model) for research by category of ability, to establish the average number of researchers available to undertake research. This is done in recognition that there must be allocations of time for teaching and other important duties.
Rights and permissions
About this article
Cite this article
Nicholls, M., Cargill, B. & Dhir, K. Using OR for diagnosis and facilitation in change programmes: a university application. J Oper Res Soc 55, 440–452 (2004). https://doi.org/10.1057/palgrave.jors.2601658
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1057/palgrave.jors.2601658