Abstract
Sensitivity and stability for Banker's model of Stochastic Data Envelopment Analysis (SDEA) is studied in this paper. In the case of the DEA model, necessary and sufficient conditions to preserve the efficiency of efficient decision-making units (DMUs) and the inefficiency of inefficient DMUs are obtained for different perturbations of data in the model. The cases of perturbations of all inputs, of perturbations of output and of the simultaneous perturbations of output and all inputs are considered. An illustrative example is provided.

Similar content being viewed by others
References
Asgharian M, Khodabakhshi M and Neralić L (2010). Congestion in stochastic data envelopment analysis: An input relaxation approach. International Journal of Statistics and System Science 5 (1–2): 84–106.
Banker RD (1988). Stochastic data envelopment analysis. Working Paper, Carnegie Mellon University, http://astro.temple.edu/~banker/DEA/18.pdf, accessed 27 November 2012.
Banker RD (1993). Maximum likelihood, consistency and data envelopment analysis: A statistical foundation. Management Science 39 (10): 1265–1273.
Banker RD, Das S and Datar SM (1989). Analysis of cost variances for management control in hospitals. Research in Governmental and Nonprofit Accounting 5: 269–292.
Banker RD, Datar SM and Kemerer CF (1991). A model to evaluate variables impacting the productivity of software maintenance projects. Management Science 37 (1): 1–18.
Charnes A and Neralić L (1990). Sensitivity analysis of the additive model in data envelopment analysis. European Journal of Operational Research 48 (3): 332–341.
Charnes A and Neralić L (1992a). Sensitivity analysis in data envelopment analysis 3. Glasnik Matematički 27 (1): 191–201.
Charnes A and Neralić L (1992b). Sensitivity analysis of the proportionate change of inputs (or outputs) in data envelopment analysis. Glasnik Matematički 27 (2): 393–405.
Charnes A, Cooper WW, Lewin AY, Morey RC and Rousseau J (1985). Sensitivity and stability analysis in DEA. Annals of Operations Research 2 (1): 139–156.
Collier T, Johnson AL and Ruggiero J (2011). Technical efficiency estimation with multiple inputs and multiple outputs using regression analysis. European Journal of Operational Research 208 (2): 153–160.
Cooper WW, Huang ZM, Lelas V, Li SX and Olesen OB (1998). Chance constrained programming formulations for stochastic characterizations of efficiency and dominance in DEA. Journal of Productivity Analysis 9 (1): 53–79.
Cooper WW, Li S, Seiford LM, Tone K, Thrall RM and Zhu J (2001). Sensitivity and stability analysis in DEA: Some recent developments. Journal of Productivity Analysis 15 (3): 217–246.
Cooper WW, Deng H, Huang ZM and Li SX (2002). Chance constrained programming approaches to technical efficiencies and inefficiencies in stochastic data envelopment analysis. Journal of the Operational Research Society 53 (12): 1347–1356.
Cooper WW, Deng H, Huang ZM and Li SX (2004). Chance constrained programming approaches to congestion in stochastic data envelopment analysis. European Journal of Operational Research 155 (2): 487–501.
Cooper WW, Seiford LM and Tone K (2006). Introduction to Data Envelopment Analysis and Its Uses with DEA-Solver Software and References. Springer Science+Business Media: New York.
Desai A, Ratick SJ and Shinar AP (2005). Data envelopment analysis with stochastic variations in data. Socio-Economic Planning Sciences 39 (2): 147–164.
Golub GH and Van Loan CF (1983). Matrix Computations. Johns Hopkins University Press: Baltimore, MD.
Grosskopf S (1996). Statistical inference and nonparametric efficiency: A selective survey. Journal of Productivity Analysis 7 (2–3): 161–176.
Huang ZM and Li SX (1996). Dominance stochastic models in data envelopment analysis. European Journal of Operational Research 95 (2): 390–403.
Huang ZM and Li SX (2001). Stochastic DEA models with different types of input-output disturbances. Journal of Productivity Analysis 15 (2): 95–113.
Kao C and Liu ST (2009). Stochastic data envelopment analysis in measuring the efficiency of Taiwan commercial banks. European Journal of Operational Research 196 (1): 312–322.
Khodabakhshi M (2009). Estimating most productive scale size with stochastic data in data envelopment analysis. Economic Modelling 26 (5): 968–973.
Khodabakhshi M (2010a). Chance constrained additive input relaxation model in stochastic data envelopment analysis. International Journal of Information and Systems Sciences 6 (1): 99–112.
Khodabakhshi M (2010b). An output-oriented super-efficiency measure in stochastic data envelopment analysis: Considering Iranian electricity distribution companies. Computers & Industrial Engineering 58 (4): 663–671.
Khodabakhshi M and Asgharian M (2009). An input relaxation measure of efficiency in stochastic data envelopment analysis. Applied Mathematical Modelling 33 (4): 2010–2023.
Khodabakhshi M, Asgharian M and Gregoriu GN (2010). An input-oriented super-efficiency measure in stochastic data envelopment analysis: Evaluating chief executive officers of US public banks and thrifts. Expert Systems With Applications: An International Journal 37 (3): 2092–2097.
Kousmanen T and Johnson AL (2010). Data envelopment analysis as nonparametric least-squares regression. Operations Research 58 (1): 149–160.
Kousmanen T and Kortelainen M (2012). Stochastic non-smooth envelopment of data: Semi-parametric frontier estimation subject to shape constraints. Journal of Productivity Analysis 38 (1): 11–28.
Li SX (1998). Stochastic models and variable returns to scales in data envelopment analysis. European Journal of Operational Research 104 (3): 532–548.
Morita H and Seiford LM (1999). Characteristics on stochastic DEA efficiency—Reliability and probability being efficient. Journal of the Operations Research Society of Japan 42 (4): 389–404.
Murty KG (1983). Linear Programming. John Wiley & Sons: New York.
Neralić L (1997). Sensitivity in data envelopment analysis for arbitrary perturbations of data. Glasnik Matematički 32 (2): 315–335.
Neralić L (1998). Sensitivity analysis in models of data envelopment analysis. Mathematical Communications 3 (1): 41–59.
Neralić L (2004). Preservation of efficiency and inefficiency classification in data envelopment analysis. Mathematical Communications 9 (1): 51–62.
Neralić L and Wendell RE (2004). Sensitivity in data envelopment analysis using an approximate inverse matrix. Journal of the Operational Research Society 55 (11): 1187–1193.
Ray SC (2004). Data Envelopment Analysis Theory and Techniques for Economics and Operations Research. Cambridge University Press: Cambridge.
Ruggiero J (2004). Data envelopment analysis with stochastic data. Journal of the Operational Research Society 55 (9): 1008–1012.
Sengupta JK (1987). Data envelopment analysis for efficiency measurement in the stochastic case. Computers and Operations Research 14 (2): 117–129.
Sengupta JK (1998). Stochastic data envelopment analysis: A new approach. Applied Economics Letters 5 (5): 287–290.
Sengupta JK (2000a). Efficiency analysis by stochastic data envelopment analysis. Applied Economic Letters 7 (6): 379–383.
Sengupta JK (2000b). Dynamic and Stochastic Efficiency Analysis: Economics of Data Envelopment Analysis. World Scientific Publishing Company: Singapore.
Sueyoshi T (2000). Stochastic DEA for restructure strategy: An application to a Japanese petroleum company. Omega 28 (4): 385–398.
Watson J, Wickramanayke J and Premachandra IM (2011). The value of Morningstar ratings: Evidence using stochastic data envelopment analysis. Managerial Finance 37 (2): 94–116.
Acknowledgements
This research was partly supported by Grant No. 067-0000000-1076 of the Ministry of Science, Education and Sports of the Republic of Croatia. The authors are grateful to two anonymous referees whose suggestions improved the paper.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A
On stochastic data envelopment analysis
SDEA is a part of DEA methodology in which stochastic models based on the possibility of random variations in input–output data are studied. There are different approaches to stochastic DEA (see, for example, Banker, 1988, 1993; Ray, 2004, Chapter 12, pp 307–326; and the survey paper Grosskopf, 1996). Chance-constrained programming formulations for stochastic characterizations of efficiency and dominance in DEA were studied by Cooper et al (1998). In a study by Cooper et al (2002), ‘ordinary DEA formulations are replaced with stochastic counterparts in the form of a series of chance constrained programming models’, with ‘emphasis on technical efficiencies and inefficiencies which do not require costs or prices, but which are nevertheless basic in that the achievement of technical efficiency is necessary for the attainment of ‘allocative’, ‘cost’ and ‘other types of efficiencies’. Desai et al (2005), considering chance-constrained formulations of DEA that allow random variations in the data, ‘suggest that, in keeping with the tradition of DEA, the simulation approach allows users to explicitly consider different data generating processes and allows for greater flexibility in implementing DEA under stochastic variations in data’. There are chance-constrained programming approaches to congestion in stochastic DEA in a study by Cooper et al (2004). Congestion in stochastic DEA based on the input relaxation approach was studied by Asgharian et al (2010). The deterministic equivalent to the stochastic congestion model was obtained, and when allowable limits of data variations for evaluating DMU were permitted, sensitivity analysis was studied. Huang and Li (1996) developed stochastic models in DEA with the possibility of random variations in input–output data. Dominance structures on the DEA envelopment side are used to incorporate the model builder's preferences and to discriminate efficiencies among DMUs. The efficiency measure can be characterized by solving a chance-constrained programming problem. The relationships between the general stochastic DEA models and the conventional DEA models are discussed. Stochastic DEA models with different types of input–output disturbances were studied by Huang and Li (2001). An input relaxation measure of efficiency in stochastic DEA was studied by Khodabakhshi and Asgharian (2009). They introduced a stochastic version of an input relaxation model in DEA, which ‘allows more changes in the input combinations of DMUs than those in the observed inputs of evaluating DMU’. A non-linear deterministic equivalent to this stochastic model under fairly general conditions can be replaced by an ordinary deterministic DEA model. The model is illustrated using a real data set. Khodabakhshi (2009) studied the estimating of the most productive scale size with stochastic data in DEA. To solve the stochastic model, a deterministic non-linear equivalent is obtained, which can be converted to a quadratic program. Using the proposed approach, the performance of software companies is evaluated. A chance-constrained additive input relaxation model in stochastic DEA was studied by Khodabakhshi (2010a). An input-oriented super-efficiency measure in stochastic DEA was studied by Khodabakhshi et al (2010). Sensitivity analysis of the proposed super-efficiency model is discussed. The results are illustrated by evaluating chief executive officers of US public banks and thrifts. For an output-oriented super-efficiency measure in stochastic DEA when considering Iranian electricity distribution companies, see Khodabakhshi (2010b). In a study by Li (1998), stochastic DEA models were developed and the stochastic efficiency measure of a DMU was defined through joint probabilistic comparisons of inputs and outputs with other DMUs. The measure can be characterized by solving a chance-constrained programming problem. An analysis of stochastic variable returns to scale was also developed. Morita and Seiford (1999) ‘consider an efficiency analysis of DMUs by using inputs and outputs data with stochastic variations, and discuss some stochastic measures of efficiency taking into account of the measurement error. The most interesting characteristic is reliability and robustness of the efficiency result’. Ruggiero (2004) considers ‘panel data models of efficiency estimation. One DEA model that has been used averages cross-sectional efficiency estimates across time and has been shown to work relatively well. It is shown that this approach leads to biased efficiency estimates and provides an alternative model that corrects this problem. The approaches are compared using simulated data for illustrative purposes’. Sengupta (1987) studied DEA for efficiency measurement in a stochastic case with some empirical applications in the measurement of the efficiency of public schools to test the sensitivity and robustness of efficiency ranking and measurement. Sengupta (1998) developed ‘pre- and post-optimality analysis of input–output data as a practical method of Farell-type efficiency measurement. Filtering of noise and specifying the optimal output distributions provide the basic tools, which are applied to time series data for international airlines’. In a study by Sengupta (2000a), ‘the nonparametric approach of efficiency analysis is generalized in the stochastic case, when the input prices and capital adjustment costs vary. An empirical application illustrates the economic applications’. One of the features of the study by Sengupta (2000b) is the consideration of ‘the stochastic aspects of DEA efficiency in terms of the stochastic dominance approach’. ‘Various applied aspects of dynamic and stochastic efficiency theory are also explained, so that the DEA model can be empirically implemented in diverse economic situations’. Kao and Liu (2009) studied measuring the efficiency of Taiwan commercial banks using stochastic DEA. The results obtained show that ‘when multiple observations are available for each DMU, the stochastic-data approach produces more reliable and informative results than the average-data and interval-data approaches do’. Sueyoshi (2000) presented a stochastic DEA model and reformulated it in a manner that the stochastic model can incorporate future information. The proposed approach was applied to plan the restructuring strategy of a Japanese petroleum company. Watson et al (2011) proposed the application of a simulation approach to stochastic DEA and contributed to the existing finance literature by examining whether the ratings of the Morningstar in Australia provide useful information for an investor by way of investigating the efficiency of domestic Australian equity funds. The benefit of the paper for investors and fund managers is the improved efficiency of stochastic DEA as a tool for measuring the efficiency of DMUs within investment fund markets. Kousmanen and Johnson (2010) show ‘that DEA can be alternatively interpreted as a nonparametric least-squares regression subject to shape constraints on the frontier and sign constraints on residuals’. The DEA model that is observed is a standard multiple input and single output model. They also developed a non-parametric variant of the corrected ordinary least-squares method and show that this method is consistent and asymptotically unbiased. Collier et al (2011) developed ‘deterministic cross sectional and stochastic panel data regression models that allow multiple inputs and outputs’. They also show how technical efficiency can be estimated without input price data using regression models. Kousmanen and Kortelainen (2012) examined ‘an encompassing semiparametric frontier model that combines the DEA-type non-parametric frontier, which satisfies monotonicity and concavity, with the Stochastic Frontier Analysis (SFA)-style homoscedastic composite error term’. A new two-stage method is proposed to estimate this model.
Appendix B
Perturbations of output and simultaneous perturbations of output and all inputs
Perturbations of output for the case of the DEA model
Let us consider a decrease of output of all efficient DMUs

and an increase of output of all inefficient DMUs

We are interested in the conditions that are necessary and sufficient to preserve the efficiency of all efficient DMUs and the inefficiency of all inefficient DMUs under the perturbations (B.1) and (B.2). Let us point out that perturbations (B.1) and (B.2) are accompanied by the alterations of the vector P0 of the right-hand side coefficients of the linear programming problem (20)–(22). Let  be the perturbed vector P0 obtained using the perturbations (B.1) and (B.2).
be the perturbed vector P0 obtained using the perturbations (B.1) and (B.2).
Theorem B.1
-
Let us consider the perturbations (B.1) and (B.2) of the output of all DMUs with the perturbed vector
 . Conditions
. Conditions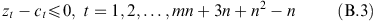
and

are necessary and sufficient to preserve the efficiency of all efficient DMUs and the inefficiency of all inefficient DMUs under the perturbations (B.1)–(B.2).
Proof:
-
Perturbations (B.1)–(B.2) do not change the optimality conditions, but may disturb the feasibility of the solution (29). The optimality conditions (B.3) for the solution (29) of the linear programming problem (20)–(22) have not been changed because vector c B of the coefficients of optimal basic variables in the objective function (20) and optimal basis matrix B have not been changed. The primal feasibility of the basic variables is preserved because of the conditions (B.4). This means that the efficiency of efficient DMUs and the inefficiency of inefficient DMUs are preserved and prove the theorem. □
Remark 2
-
Conditions (B.4) together with constraints in (B.1)–(B.2) give the system of inequalities in α j , j=1, …, n. For each point (α1*, α2*, …, α n *) in the solution set S α of that system of inequalities, the efficiency of all efficient DMUs and the inefficiency of all inefficient DMUs will be preserved, with perturbations (B.1) of the output of efficient DMUs and perturbations (B.2) of the output of inefficient DMUs. These changes can be considered also in the production possibility set. At some limit points, the status of DMUs could be changed from efficient to inefficient and vice versa.
Example 1
-
(continued). Let us consider again the data for example 1 in Table 1. As before, the linear programming problem (20)–(22) is (51)–(53) with solution (54). The optimal basis matrix is (55) with the inverse (56). The set of indices of efficient DMUs is E={1, 3} and the set of indices of inefficient DMUs is N={2}. Let us consider a decrease of output of DMU1 and DMU3

and an increase of output of DMU2

The perturbed vector of the right-hand side coefficients is

The conditions (B.4) in Theorem B.1, together with the constraints in (B.5)–(B.6), give the following system of inequalities


The solution set S α (see Figure B1) of the system of inequalities (B.8)–(B.9) is determined by

For each point (α1*, α2*,α3*)∈S α under the corresponding perturbations (B.5)–(B.6), the efficiency of DMU1 and DMU3 will be preserved and the inefficiency of DMU2 will be preserved too.
In the case α1=α2=α3=α from (B.10), we get the solution set S̄
α
=[0, 3/4]. For α∈[0, 3/4] using the corresponding perturbations (B.5)–(B.6), we can get in the production possibility set the regions of efficiency  with A1(2, 2.25) and
with A1(2, 2.25) and  with A3(6, 4.25) for DMU1 and DMU3, respectively. (The region of efficiency (inefficiency) is a part of the production possibility set in which the efficiency of an efficient DMU (the inefficiency of an inefficient DMU) is preserved under the specified perturbations of data. See Neralić, 1997, Definition 1, p. 327). We can also get the region of inefficiency
with A3(6, 4.25) for DMU1 and DMU3, respectively. (The region of efficiency (inefficiency) is a part of the production possibility set in which the efficiency of an efficient DMU (the inefficiency of an inefficient DMU) is preserved under the specified perturbations of data. See Neralić, 1997, Definition 1, p. 327). We can also get the region of inefficiency  with A2(5, 3.75) for DMU2 (see Figure B2). Let us point out that for α=(3/4), the status of DMU2 is changed from inefficient to efficient, with the preservation of efficiency of DMU1 and DMU3. Therefore, in order to preserve the efficiency of efficient DMUs and the inefficiency of inefficient DMUs, α=(3/4) should be excluded from the solution set S̄
α
=[0, 3/4].
with A2(5, 3.75) for DMU2 (see Figure B2). Let us point out that for α=(3/4), the status of DMU2 is changed from inefficient to efficient, with the preservation of efficiency of DMU1 and DMU3. Therefore, in order to preserve the efficiency of efficient DMUs and the inefficiency of inefficient DMUs, α=(3/4) should be excluded from the solution set S̄
α
=[0, 3/4].
Simultaneous perturbations of output and all inputs for the case of the DEA model
Let us consider for the case of c<cM in the linear programming problem (20)–(22), a simultaneous decrease of output of all efficient DMUs

an increase of output of all inefficient DMUs

an increase of inputs of efficient DMUs

and a decrease of inputs of inefficient DMUs

Perturbations of output (B.11)–(B.12) are accompanied by alterations in the vector of the right-hand side coefficients P0, and perturbations of inputs (B.13)–(B.14) are accompanied by alterations of the inverse matrix B−1 of the optimal basis matrix B. As before, we will use the notation



and

in order to get the following result.
Theorem B.2
-
Let us consider the simultaneous perturbations (B.11)–(B.12) of output and the perturbations (B.13)–(B.14) of all inputs with
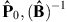 and ẑ
t
, t=1, 2, …, mn+3n+n2−n. Conditions
and ẑ
t
, t=1, 2, …, mn+3n+n2−n. Conditions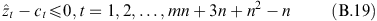
and

are necessary and sufficient to preserve the efficiency of all efficient DMUs and the inefficiency of all inefficient DMUs under the simultaneous perturbations (B.11)–(B.14).
Proof:
-
Just as in the proof of Theorem 2 and Theorem B.1, conditions (B.19) are optimality conditions for the perturbed linear programming problem (20)–(22), based on the simultaneous perturbations (B.11)–(B.12) of output and perturbations (B.13)–(B.14) of inputs, with ẑ t in (B.18) and the same vector c B of coefficients of optimal basic variables in the objective function (20). The optimal basis matrix B has been changed according to (B.16) and its inverse has also been changed according to (B.17). Conditions (B.20) give the primal feasibility for basic variables using the inverse (B.17) of the perturbed optimal basis matrix and the perturbed vector
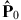 of the vector P0 of the right-hand side coefficients in the linear programming problem (20)–(22). This means that the theorem is proved. □
of the vector P0 of the right-hand side coefficients in the linear programming problem (20)–(22). This means that the theorem is proved. □
Remark 3
-
Conditions (B.19) and (B.20) in Theorem B.2, together with the constraints (B.11)–(B.14), give the system of inequalities in α j , j=1, 2, …, n, β ij , i=1, 2, …, m, j=1, 2, …, n. For each point (α j *, β ij *), i=1, 2, …, m, j=1, 2, …, n in the solution set S αβ of that system of inequalities, the efficiency of all efficient DMUs and the inefficiency of all inefficient DMUs will be preserved, with perturbations (B.11)–(B.12) of output and perturbations (B.13)–(B.14) of all inputs. These perturbations can also be considered in the production possibility set. At some limit points, the status of DMUs could be changed from efficient to inefficient and vice versa.
Example 1
-
(continued). Let us consider again data for example 1 in Table 1. As before, the set of indices of efficient DMUs is E={1, 3} and the set of indices of inefficient DMUs is N={2}. Let us consider the simultaneous perturbations of output and input. We decrease the output of DMU1 and of DMU3

and increase the output of DMU2

We also increase the input of the efficient DMU1 and the efficient DMU3

and decrease the input of the inefficient DMU2

The conditions (B.19) in Theorem B.2 give the system of inequalities (64) in β1, β2, β3 as before and conditions (B.20) give the system of inequalities in α1, α2, α3, β1, β2, β3


We get additional inequalities from the constraints (B.21)–(B.24)

The system of inequalities (B.25)–(B.27) is non-linear and it is not easy to solve. In the case α1=α2=α3=α and β1=β2=β3=β from (64) and (B.25)–(B.27), we get solution set S̄ αβ which is determined by

This is the triangle ΔOAB in the coordinate system αOβ with O(0, 0), A(0.75, 0) and B(0, 1.5) (see Figure B3). For (α, β)∈S̄
αβ
using the corresponding perturbations (B.21)–(B.24), we can get in the production possibility set the regions of efficiency ΔP1A1B1 with P1(2, 3), A1(2, 2.25), B1(3.5, 3) and ΔP3A3B3 with P3(6, 5), A3(6, 4.25), B3(7.5, 5) for DMU1 and DMU3, respectively. We can also get the region of inefficiency ΔP2A2B2 with P2(5, 3), A2(5, 3.75), B2(3.5, 3) for DMU2 (see Figure B4). Let us point out that for (α, β) from the segment  in Figure B3, the status of DMU2 is changed from inefficient to efficient, with a preservation of the efficiency of DMU1 and DMU3. Therefore, in order to preserve the efficiency of efficient DMUs and the inefficiency of inefficient DMUs, the segment
in Figure B3, the status of DMU2 is changed from inefficient to efficient, with a preservation of the efficiency of DMU1 and DMU3. Therefore, in order to preserve the efficiency of efficient DMUs and the inefficiency of inefficient DMUs, the segment  should be excluded from the solution set S̄
αβ
.
should be excluded from the solution set S̄
αβ
.
Rights and permissions
About this article
Cite this article
Banker, R., Kotarac, K. & Neralić, L. Sensitivity and stability in stochastic data envelopment analysis. J Oper Res Soc 66, 134–147 (2015). https://doi.org/10.1057/jors.2012.182
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1057/jors.2012.182




 . Conditions
. Conditions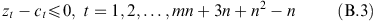



 and ẑ
t
, t=1, 2, …, mn+3n+n2−n. Conditions
and ẑ
t
, t=1, 2, …, mn+3n+n2−n. Conditions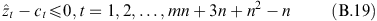

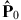 of the vector P0 of the right-hand side coefficients in the linear programming problem (20)–(22). This means that the theorem is proved. □
of the vector P0 of the right-hand side coefficients in the linear programming problem (20)–(22). This means that the theorem is proved. □
